海水濃度對藍綠激光通信的影響分析

王 菲，姬冠妮

（西安交通工程學院，陜西 西安 710300）

0 引 言

隨著水下通信技術在水下捕撈、探測以及安防等領域的廣泛應用，水下通信技術已成為當前水下信息獲取的關鍵技術。當前，海水通信采用的聲學通信方法由于傳輸速率低、可用帶寬有限等缺陷應用受限，而光學通信技術可以克服這些缺陷。由于藍綠光工作頻率高、方向性好且抗干擾能力強[1]，在海水中傳輸時比其他光衰小等優點，使得藍綠激光通信技術在海水通信中具有巨大的研究價值。但是，由于海水成分的復雜性，藍綠激光的傳輸在一定程度上受海水信道的影響。

當前研究大都處于海水信道的理論傳輸模型和蒙特卡洛仿真分析階段。美國林肯實驗室的Andrew.S[2]采用蒙特卡洛模擬法仿真海水的散射環境，得到通過使用窄光束光源可獲得Gb/s速率的水下通信系統的理論分析。目前的研究結果均未涉及接收機接收位置與接收功率之間的對應關系，由此可知海水信道沒有一個較完善的模型，無法準確進行信道估計，從而對水下光通信系統的設計產生了影響。

1 理論分析

1.1 海水信道光學特性

對于海水中成分的研究，主要研究其兩種重要的光學特性：一是海水成分對光的吸收作用；二是其對光的散射作用[3]。同時，這兩種光學性質會影響光在水下的傳輸特性，因此海水中的總衰減為吸收和散射這兩種作用導致的衰減之和。

本文涉及到的這幾種海水成分對光學特性有著重要影響，分別為海水水分子、浮游植物、非色素懸浮微粒和黃色物質[4-5]。其中，海水的總衰減系數c為：

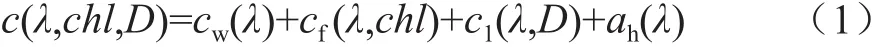
式中，cw(λ)表示海水水分子的衰減系數；cf(λ,chl)表示浮游植物衰減系數，與浮游植物含有的葉綠素a濃度chl有關；c1(λ,D)表示非色素懸浮微粒的衰減系數，其中非色素懸浮微粒的散射系數與濃度D有關，而吸收系數與其濃度無關[6]；ch(λ)代表黃色物質的吸收系數，黃色物質對光只有吸收作用，而無散射作用。

由于海水中濃度的不同，對于海水信道的模擬分析一般被分成3類：第Ⅰ類海水為遠洋海域海水，第Ⅱ類海水為近海海域海水，第Ⅲ類海水為海灣海域海水。本文對這3類海水的光學特征參數的研究采用的是Petzold的測量值[7]。Petzold測量的水質參數如表1所示，表1中a為海水的吸收系數，b為海水的散射系數，c為海水總衰減系數。

表1 三類海水Petzold測量的水質參數 /m-1

參照表1的水質參數，選取第Ⅰ類海水的總衰減系數c(λ,chl,D)=0.204 7m-1，其中葉綠素a的濃度chl=0.03 mg/m3，非色素懸浮微粒濃度D=0.01mg/L；第Ⅱ類海水的總衰減系數c(λ,chl,D)=0.463 4m-1，其中葉綠素a的濃度chl=0.3 mg/m3，非色素懸浮微粒濃度D=0.8 mg/L。由于第Ⅲ類海水的衰減系數c很大，導致文中的蒙特卡洛模擬仿真時間過長，因此為了減少仿真時間。本文選取第三種海水為葉綠素a濃度為北黃海近海域的全年平均濃度chl=5 mg/m3、非色素懸浮微粒濃度D=1 mg/L[8]的水質參數，此時海水總衰減系數c(λ,chl,D)=1.204 7m-1。

1.2 海水信道蒙特卡洛仿真原理

蒙特卡洛模擬法是把激光看作一系列的光子，然后追蹤每個光子的運動狀態，最后利用追蹤到的光子的統計分布表示激光的分布特征[9-10]。由于海水中微粒的分布狀態完全隨機，所以利用蒙特卡洛方法模擬仿真時，運動狀態的光子會與海水中存在的微粒發生隨機碰撞。光子的模擬過程如下[11]。

（1）光子的產生。本文的蒙特卡洛模擬仿真過程中，將激光器發射的光源看成是點光源。本次仿真過程中發射端的發射光功率為-7 dBm，即發射光子數接近106個。

（2）光子的傳輸過程。光子傳輸一定距離dm后到達散射點。隨機步長可表示為式中r代1表[0，1]間均勻分布的隨機數，c表示海水總衰減系數。

（3）下一個碰撞點位置。仿真中假設光子經歷了m次碰撞，下一個碰撞點表示為rm+1，則其下一個碰撞點的位置通過dm表示，碰撞后的位置狀態為：

（4）碰撞后的運動方向。由于水中的顆粒直徑與光波長的關系為r/λ≈1，遵循Mie散射理論，散射特性可用體積散射函數β(θ)描述，本文采用H-G函數的體積散射函數為：

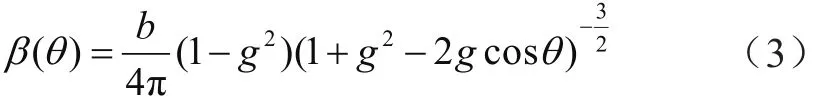
式中，g為散射余弦的平均值，g=〈cosθ〉=0.924[12]，則散射后光子的散射方向(φm,θm)可由式（4）決定。

式中，θm表示光子的散射角，它是由光在水下的散射特性決定的；φm為方位角；r2、r3分別為[0，1]間均勻分布的隨機數，則光子碰撞后的方向矢量可表示為：

若光子在模擬仿真過程中的運動方向非常接近z軸，則新的方向可表示為：

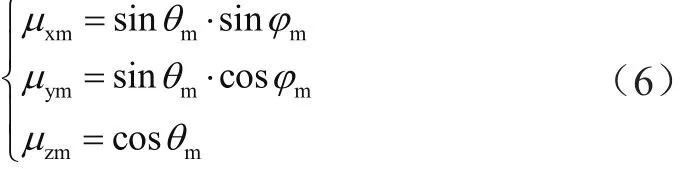
（5）碰撞后的權值。光子在模擬仿真過程中碰撞后的權值可表示為Wm+1=Wm·ω0[13]，式中ω0為海水中散射系數b與總衰減系數c的比值。

2 海水信道仿真及擬合分析

文中采用波長為530 nm激光作為發射光源。為避免本次仿真時間過長，本文選取模擬仿真的發射光功率Pt=-7 dBm，發射角θ=0.78 mrad，光傳輸距離是1 m，且采用形如平頂高斯函數對蒙特卡洛仿真結果進行擬合，即通過修正平頂高斯函數中的參數N和b實現擬合。通過平頂高斯函數擬合后的曲線如圖1所示。

由圖1可知，隨著海水雜質濃度的增加，光斑中心位置接收功率逐漸減小，光斑逐漸擴展但是擴展不明顯。從接收光斑的波形來看，僅僅是接收面的光功率的平坦度有明顯改變，說明海水水質參數的變化在一定區域內將影響接收機的接收范圍。

3 海水信道無線激光傳輸模型的建立與分析

3.1 激光傳輸模型的建立

利用平頂高斯函數擬合的海水中的激光傳輸功率與傳輸距離及任意位置關系的表達式即海水信道無線激光的傳輸模型：

式中，x表示接收點距離光斑中心位置的偏差值，y是接收端的接收功率，d是激光傳輸距離，c是海水衰減系數。

3.2 激光接收功率與接收機接收位置的對比關系

在無線激光傳輸仿真模型中，當選取不同的海水水質參數，海水總衰減系數分別為c=0.204 7 m-1、c=0.463 4 m-1、c=1.240 7 m-1時，可計算出接收機在不同光子位置時接收功率值，見表2。

表2 接收機在不同位置時的功率值

從表2可以得出，利用無線激光傳輸仿真模型可以得到接收機在任意位置的功率衰減值，而理論傳輸模型并未體現出接收光功率隨光子位置變化的關系，因此無線激光傳輸模型彌補了理論傳輸模型的不足。

圖1 海水中光傳輸接收的光功率與光斑位置擬合曲線

4 結 論

通過對不同水域海水特性進行分析與仿真，得到海水不同水質條件下的激光傳輸特性，建立了信道的激光傳輸模型。當海水中激光傳輸距離一定時，激光器在FOV范圍內接收的光功率主要集中在光斑中心附近位置；當激光器遠離光斑中心附近位置后，光斑快速擴展，功率快速下降。固定接收機在光斑的某一位置，當傳輸距離和海水濃度確定時，可利用激光傳輸模型得到接收機在光斑中任意位置的相對接收功率，從而為水下藍綠激光傳輸系統設計提供參考依據，彌補了海水信道理論傳輸模型的不足。