基于插入損失的魚雷動力艙段振動傳遞評估方法

曹 浩，王志杰，趙昌利

（中國船舶重工集團公司第七〇五研究所，陜西 西安 710077）

0 引言

魚雷航行時產生的噪聲是暴露攻擊潛艇和魚雷方位的實質因素。動力裝置的機械、流體振動是魚雷自噪聲和輻射噪聲的主要來源，強烈的振動和噪聲直接影響到魚雷武器的隱身性、攻擊效能、安全性和可靠性[1-5]。

振動性能是評價魚雷動力系統優劣的主要方面之一。振動控制問題總體來說應該從3個方面入手：振源識別、傳遞路徑分析及采取振動隔離措施。準確的辨識傳遞路徑并獲得不同傳遞路徑的振動貢獻量，是采取隔振措施的前提[6-12]。

對于動力艙段，其結構復雜、激勵來源豐富，且每種激勵都會通過多重或者多維的傳遞路徑，將振動傳遞到殼體上。發動機和海水泵是魚雷動力艙段的主要振動源，為了降低振動源向魚雷殼體振動傳遞，工程上通常使用柔性海水管、隔振器等隔振結構阻尼振動能量的傳遞。

文獻[13]用四端參數法建立了魚雷動力裝置振動傳遞數學模型，探討了整圈式隔振器的幾何結構、橡膠硬度和阻尼等參數對隔振特性的影響。但在動力艙段設計初期，發動機、海水泵、殼體的具體結構尚未形成，無法應用有限元方法預估動力艙段的動力學特性；目前未形成簡單有效的、可用于評估隔振結構效果的計算方法。如何設計隔振結構的動力學參數和評估它們在動力艙段內的隔振效果是當前的難題。

本文將魚雷動力艙段抽象稱為由發動機和海水泵、隔振器及殼體3個子系統組成的模型，建立了由振源、傳遞路徑、響應點構成的集中參數動力學模型，在頻域內對動力學方程推導，得到了系統的穩態響應幅值表達式。結合電氣系統的插入損失概念，提出了適用于評估魚雷動力艙段隔振元件效果的速度插入損失指標。應用振動路徑隔離的方法，給出了不同振動傳遞路徑的速度插入損失評估公式。結合工程問題給出了算例，表明在設計初期可以清晰地規劃動力艙段的隔振結構的性能參數。

1 基于插入損失的評估方法

魚雷艙段通常為筒形結構，由于受到結構空間的限制，通常使用整圈式隔振器與隔振墊和柔性海水管組合的方式將動力裝置懸置在殼體上，可以高效地抑制振動向殼體的傳遞。這種隔振方式稱為整機隔振，工程應用表明設計合理的整機隔振結構對振動的隔離效果顯著。開展整機隔振結構參數設計時，通常將動力艙段簡化為圖1所示的結構。

從結構上分析，在動力艙段殼體與動力裝置之間存在隔振器與海水管2種形式的連接，其中隔振器又分為前端隔振器與后端隔振器。故在動力裝置（振動源）與動力艙段殼體（被動端）之間共存在3條傳遞路徑：前端隔振器、后端隔振器和海水管。

1.1 動力學模型

對圖1所示模型進行抽象構建了圖2所示振動傳遞路徑數學模型。從圖2所示振動模型共有3條振動傳遞路徑，分別與前隔振器、后隔振器和海水管對應。

圖1 典型魚雷動力艙段整機隔振模型Fig.1 Typical torpedo power cabin's vibration isolation model

該模型為典型的振動源-振動路徑-被動端的振動傳遞路徑模型。其中振動傳遞路徑用連接結構的剛度、阻尼 2種物理參數表征。該模型只考慮發動機的單激勵，忽略了其它輔機產生的激勵力，且振源僅在垂直方向產生激勵。其振動微分方程為

式中：M、C、K分別為質量矩陣、阻尼系數矩陣和剛度矩陣；F（t）為激勵源產生的激振力；x（t）為振動系統的振動位移矢量。按照圖2的結構，細化式（1）的質量、剛度、阻尼、位移等參數得到系數矩陣（2）。

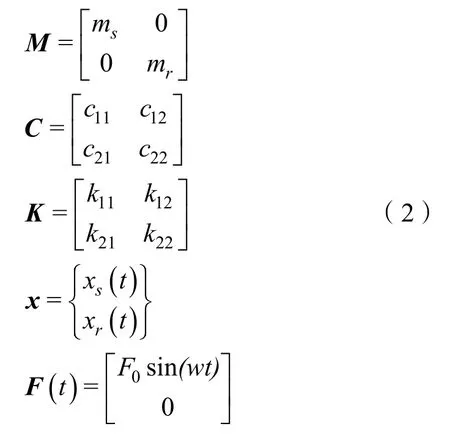
式（2）中：

上述公式中：xs（t）為發動機在激勵力作用下產生的位移；xr（t）為殼體產生的位移；kp1、cp1為海水管的剛度及阻尼系數；kp2、cp2為前隔振器的剛度及阻尼系數；kp3、cp3為后隔振器的剛度及阻尼系數。

為分析動力艙段頻域內響應，用F(t)=Feiωt來表示激勵力。頻域內方程（1）的動剛度系數矩陣為

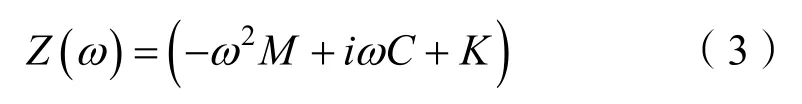
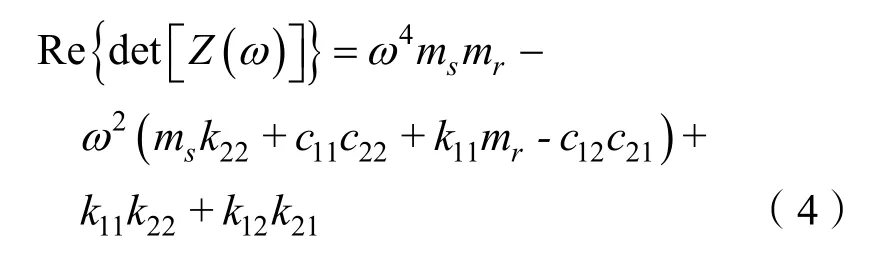
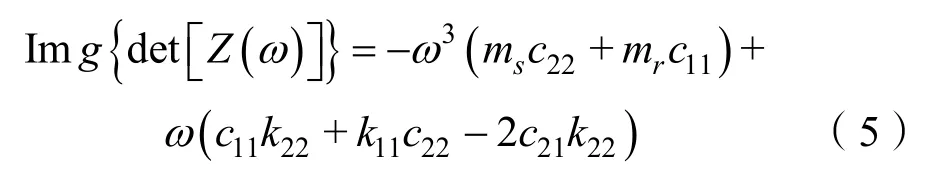
進一步推導，得到振動系統在頻域內的位移響應為

穩態下的響應幅值為

1.2 隔振效果評估

在電氣系統中，插入損失（Insertion Loss）定義為當某元件連入到系統時傳到負載的功率與該元件未連入到系統前傳到負載的功率比，單位是dB。將插入損失概念引入到機械隔振系統后，插入損失定義為采取隔振措施前后基礎響應的有效值之比的常用對數的20倍。

根據所選的基礎響應的不同，相應的可分為位移插入損失、速度插入損失、速度損失和加速度損失。速度插入損失的計算公式為

式中：為分離第i條傳遞路徑增加隔振結構后系統接被動端的速度響應；為系統在未設置隔振結構時被動端的速度響應。

以動力艙段作為研究對象，采用分離路徑法對動力艙段振動系統進行分析，以評估不同振動傳遞路徑對動力艙段殼體振動的影響。即作海水管與動力艙段殼體的連接斷開的假設，僅保留前隔振器、后隔振器與動力艙段殼體的連接。此時振動系統的各系數矩陣分別為

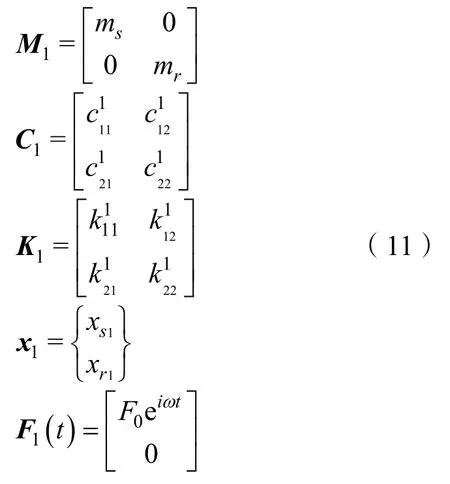
根據假設，海水管與殼體的連接斷開，故式中：

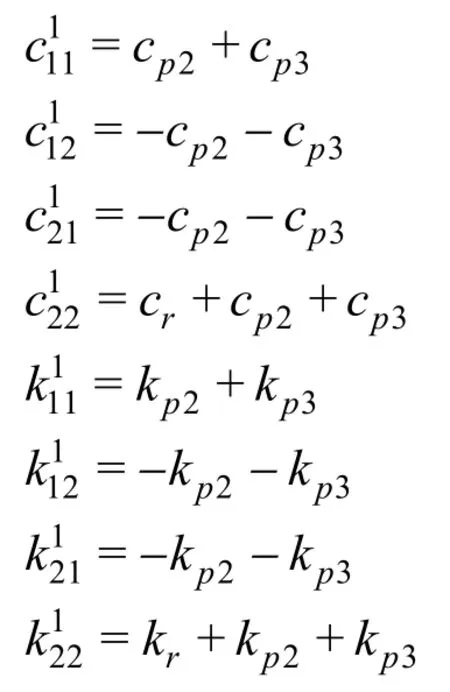
將式（11）參數應用到公式（8）、公式（9）得到系統的穩態響應，將穩態響應值應用到公式（10），得到斷開海水管情況下的速度插入損失：

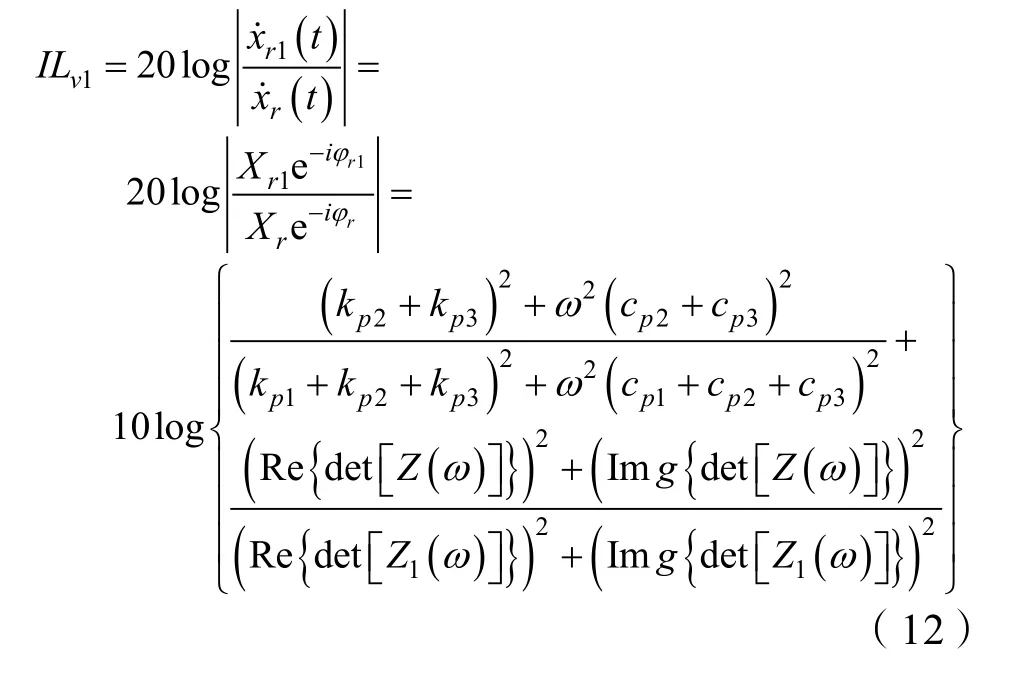
用相同的辦法，即將振動系統的前隔振器、后隔振器對應的振動傳遞路徑分別斷開后，系統的速度響應的插入損失分別為

2 數值算例

假設存在如圖1所示魚雷動力艙段，發動機加上海水泵的總質量ms=50kg ，動力艙段殼體質量mr=12kg，動力艙段與試驗臺或者其它段連接阻尼為cr=1N?s/ m ，連接剛度為kr=1.8× 106N/m 。其它參數見表1。

表1 參數列表Table 1 Parameters list

對于完整模型和分別斷開海水管、斷開前隔振器和斷開后隔振器4種狀態的動力艙段，利用模態法[14]分別計算了4種狀態動力艙段固有頻率。4種狀態動力艙段的固有頻率見表2。

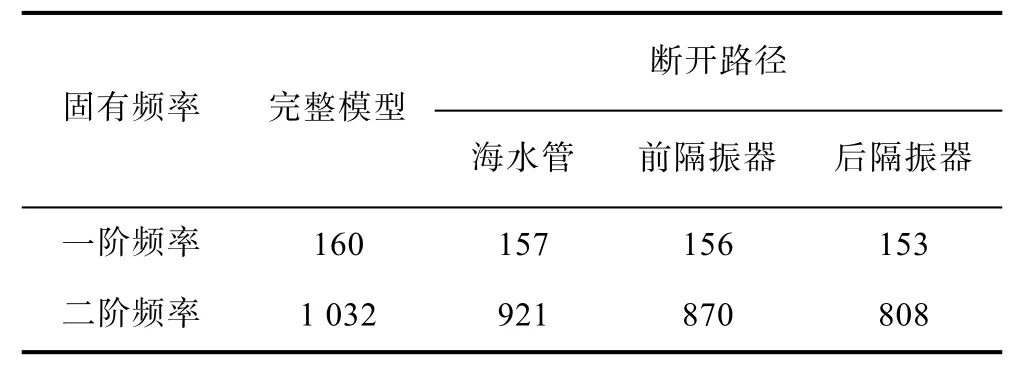
表2 4種狀態動力艙段的固有頻率Table 2 Natural frequency of power cabins at 4 states rad/s

自表2的數據可知，4種狀態的動力艙段的一階固有頻率接近，最大差值不超過7 rad/s。在二階固有頻率差別較大，最小差值為62 rad/s。

在模態域內計算了振動源和被動端之間振動傳遞函數，4種狀態動力艙段的振動傳遞函數見圖3。從圖3可知，在固有頻率附近，振動傳遞率放大非常明顯，對應于各種狀態的動力艙段，均有2個振動傳遞的峰值。

斷開不同的傳遞路徑，對于動力艙段的一階頻率影響較小，頻率基本處于153 rad/s和160 rad/s之間。斷開不同的傳遞路徑，對于動力艙段的二階頻率影響較大。相比較完整模型，斷開傳遞路徑，相當于將二階固有頻率進行了降頻，其中以斷開后隔振器降低的頻率最為明顯。斷開后隔振器將二階固有頻率降低了224 rad/s。

圖3 4種狀態動力艙段振動傳遞函數Fig.3 Vibration transmission function of power cabin at 4 states

前文推導的公式（12）、公式（13）和公式（14），分別對應斷開 3條振動傳遞路徑后，動力艙段相對于完整模型的插入損失計算公式。將動力艙段的質量、剛度和阻尼等參數代入公式，計算了斷開不同傳遞路徑后動力艙段振動能級相對于完整模型的插入損失。所得計算結果數據繪制如圖4所示。

自圖4數據知，分別斷開海水管、前隔振器和后隔振器，對于一階固有頻率附近插入損失既有正值也有負值，正值大于負值。說明在一階固有頻率處，3種斷開狀態均可取得一定的減振效果，以海水管斷開后，取得的減振效果最為明顯。對于二階固有頻率，較之完整動力艙段模型，斷開任意振動傳遞路徑都能在較低頻率取得隔振效果，以斷開后隔振器取得的隔振效果最為顯著。但是在1 000 rad/s頻率附近，振動能級明顯放大。雖然振動能級放大的量值與振動能級降低的量值相當，但從圖4亦可以清晰獲知，3種振動傳遞徑路結構使得動力艙段系統二階固有頻率附近發生移頻。

圖4 斷開不同傳遞路徑后的插入損失Fig.4 Insertion loss after cutting different transmission paths

從上數值算例可知，在尚未具備建立詳細的有限元模型條件之前，應用上述公式，結合前后隔振器或海水管等隔振環節的結構動力學參數，可以快速地給出動力艙段隔振結構的修正方向，對于工程設計具有較強的指導意義。

3 結束語

文章在頻域內推導了動力學方程，結合電路系統知識，給出了用于評估隔振效果的速度插入損失公式。將魚雷動力艙段抽象為 3個子系統組成的集中參數動力學模型，應用推導的公式可以計算出斷開不同傳遞路徑后的振動傳遞函數和插入損失。結合設計目標，可有效評估隔振器的隔振效果，并據需要，修改隔振器的設計參數。