基于棧式自編碼器的制冷系統故障診斷

羅 霄，孫 俊

(1.武漢理工大學 能源與動力工程學院，湖北 武漢 430063;2.國家水運安全中心，湖北 武漢 430063)

船舶制冷系統是船舶一個重要的輔助系統，故障診斷是保證其正常運行的重要手段之一。傳統的故障診斷方法一般采用數據特征提取與機器學習模型分類相結合的形式。但設備運行數據呈現出高維度、高數量、高非線性等特點，傳統智能診斷技術的診斷能力不足。基于深度學習的棧式自編碼器(SAE)制冷系統的故障診斷方法比傳統故障診斷方法在特征提取、泛化性、魯棒性、精度方面存在明顯的優勢[1-4]。

1 棧式自編碼器

SAE是由多個自編碼器(AE)堆棧而成，訓練SAE需先訓練AE網絡，圖1為SAE網絡結構示意圖，虛線框內為一個AE網絡結構示意圖。

AE網絡訓練過程如下。

1)計算隱藏層輸出。

Y=s(WX+b)，

(1)

式中：Y為隱藏層矩陣；W為輸入層與隱藏層之間的權值矩陣；X為輸入矩陣；b為輸入層與隱藏層之間的偏置向量；s為S型(sigmoid)函數。

2)計算輸出層函數。

Z=s(W′Y+b′)=s(WTY+b′)，

(2)

式中：Z為輸出層矩陣；W′為隱藏層與輸出層之間的權值矩陣；b′為隱藏層與輸出層之間的偏置向量。

3)構造目標函數。

J(W，b,b′)=

(3)

式中：k為輸入數據的樣本數;xi為第i個樣本的輸入；zi為第i個樣本的輸出。使用梯度下降法求得J(W,b,b′)最小值。當J(W,b,b′)迭代到最小值時，停止AE網絡訓練。

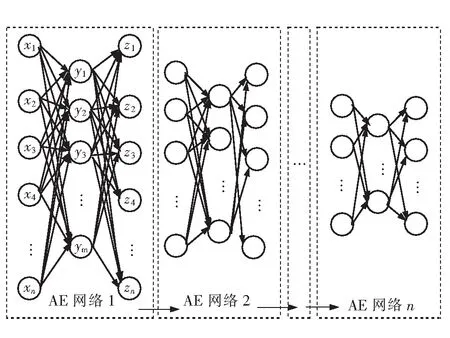
圖1 SAE網絡結構示意圖

一個AE網絡收斂后，只保留編碼過程，隱藏層再與下個網絡層組成AE網絡進行訓練，這就是通過貪婪訓練算法來預訓練SAE。預訓練完成后，在輸出層后加入一個softmax分類器，使之具備分類識別功能。最后使用有標簽數據對SAE進行微調。SAE的微調過程，與普通BP神經網絡訓練過程無異。不同點在于SAE的參數初始值是經過預訓練確定下來的值，不再是普通BP神經網絡一樣的隨機數。SAE微調過程完成說明整個SAE訓練過程完成。

2 基于SAE的故障診斷方法

基于SAE的制冷系統故障診斷流程見圖2。

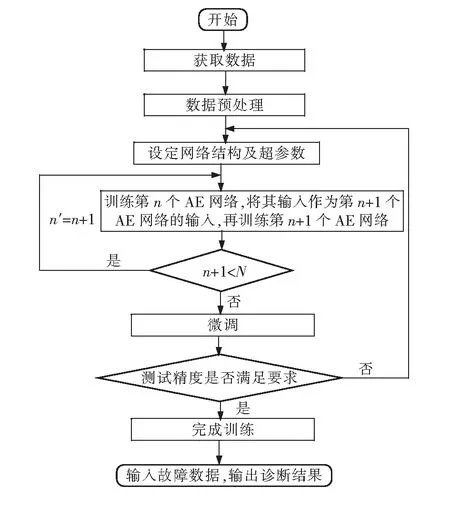
圖2 故障診斷流程圖

1)故障數據預處理。獲取故障數據，對其進行歸一化處理。

2)確定SAE的結構與超參數。通過研究分析網絡層數、批尺寸(batch_size)、學習率對網絡的影響，根據具體數據集選擇合理的網絡結構與超參數。

3)SAE的訓練。先使用無標簽數據預訓練SAE，待網絡收斂后，再使用含有故障標簽的數據進行微調。網絡再次收斂后，使用測試集中的故障數據測試網絡性能，若故障精度無法滿足要求，不斷重復2)與3)，直到測試精度滿足要求為止。

4)利用SAE進行故障診斷。將未知故障的數據輸入訓練好的SAE中，輸出診斷結果。

3 數據驗證

3.1 實驗數據

本次實驗采用ASHRAE 1043-RP項目的制冷機組故障數據。實驗對象是1臺制冷量約為316 kW的制冷機組，分別模擬了冷卻水流量不足、冷凍水流量不足、制冷劑泄漏、制冷劑過量、滑油過量、冷凝器結垢和制冷劑混入不凝性氣體這7種故障率相對較高的單發漸變故障，并對每個故障進行了4個不同嚴重等級的劃分。該系統共采集64個參數，其中48個參數由傳感器直接得出，16個參數由VisSim軟件實時計算得出。傳感器參數包含29個溫度參數，7個閥位參數，5個流量參數，5個壓力參數，2個壓縮機參數。

從ASHRAE 1043-RP項目的故障數據中，通過分層采樣選取1組正常數據與7組單發故障數據，每組單發故障數據1 000個，共8 000個故障數據，并隨機選取6 400個故障數據作為訓練集，1 600個故障數據作為測試集。

3.2 數據預處理

在訓練網絡前，需要對輸入數據進行歸一化處理，這樣可以消除不同屬性不同量級的影響，保證最后故障診斷模型的穩定性、精確性與運行速度。因為故障(輸出數據)互為獨立事件，需對其進行獨立編碼處理，才能作為網絡輸出。

3.3 網絡結構與超參數的選擇與分析

3.3.1 網絡深度的影響

先構建不同網絡層數的SAE，每層網絡神經元個數是從輸入層的64個到輸出層的8個呈等差數列排列，這里就將SAE的層數設置為3～9層，遍歷訓練集500次。不同網絡層數的測試精度與訓練時間如圖3所示。

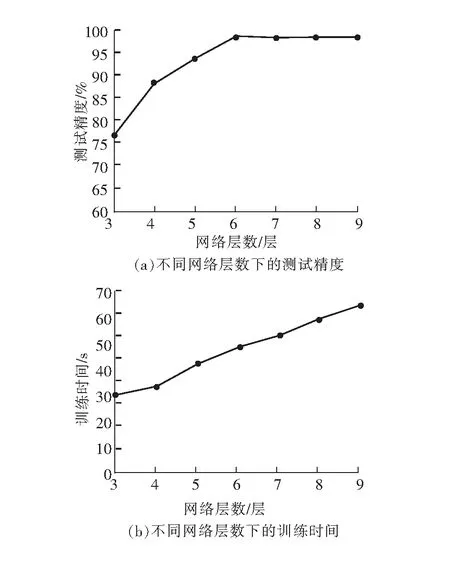
圖3 不同網絡層數的測試精度與訓練時間

由圖3可知，當網絡層數從3增加到9時，測試精度從76.3%一直增加到98%左右，說明網絡層數越深，網絡越復雜，學習能力越強，越能學習到數據中深層次的特征信息。但網絡層數從6增加到9時，測試精度卻沒有明顯變化，說明對于該數據集，6層網絡層的SAE已經可以學到足夠多、足夠深的特征信息。而3～9層網絡層數的訓練時間幾乎呈正相關(從30.2 s一直增加到64.3 s)，過深的網絡只能無意義地增加訓練時間。所以該SAE層數選擇6層最為適宜。

3.3.2 不同batch_size的影響

使用梯度下降法進行一次參數更新，需要的訓練樣本數量最小可為1，最大為訓練集的樣本總數，實際采用的是折中的數量，這個數量便是batch_size。batch_size較小時，權值更新隨機性強，但遍歷一次訓練集花費時間長，batch_size較大時，對電腦的配置有較高的要求，所以需要選擇合適的batch_size。這里將batch_size分別設為32、64、128、256、512、1 028、2 560、5 120，每個網絡遍歷訓練集500次。其測試精度與訓練時間如圖4所示。

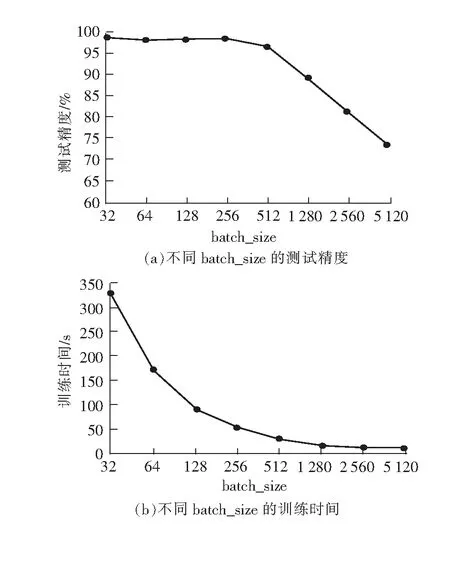
圖4 不同batch_size的測試精度與訓練時間

由圖4可知，batch_size越小，測試精度越高，說明盡管batch_size較小時網絡更新取值隨機性強，但其權值更新次數高，大多數情況下網絡同樣能夠收斂，batch_size較大時網絡遍歷一次訓練集權值更新次數少，相同迭代次數下測試精度低，要達到相同的測試精度，需要更多的遍歷次數，延長了訓練時間。但隨著batch_size減少，在相同遍歷次數下網絡訓練時間幾乎呈指數增長，也會延長訓練時間，增加訓練成本。綜上所述，本次實驗batch_size設為256最為合理。

3.3.3 不同學習率的影響

每一次網絡參數更新幅度的大小叫做學習率，也叫做步長，是眾多超參數中非常重要的一個。本次實驗將學習率分別設為1、0.1、0.01、0.001、0.000 1、0.000 01，迭代次數為500次。這些網絡的訓練誤差(cost值)與測試精度如圖5所示。

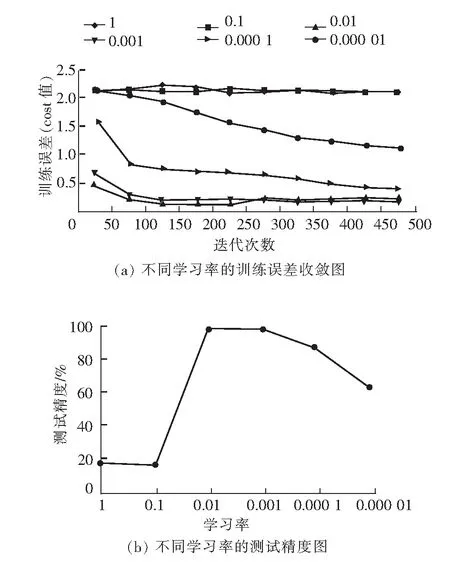
圖5 不同學習率的訓練誤差收斂圖與測試精度圖

由圖5知，當學習率為1和0.1時，cost值一直無法收斂，因為過大的學習率導致參數更新幅度過大，錯過極小值的位置，即使更新到了極小值，也會由于幅度過大，跳出極小值位置，導致測試精度過低(17.5%左右)，說明學習率為1和0.1對于該網絡太大。當學習率為0.000 1與0.000 01時，cost值下降速度變慢，特別是學習率為0.000 01時，到了迭代結束時，cost值仍有下降趨勢，測試精度也跟著下降，說明學習率過小，盡管網絡會收斂，但收斂速度太慢，導致網絡訓練時間變長，增加訓練的時間成本。當學習率為0.001時，cost值曲線下降迅速、平滑，最終測試精度理想(98%左右)，所以學習率可以選擇0.001。

3.4 與傳統故障診斷方法對比

現將SAE與PCA+SVM、BP神經網絡進行比較分析。PCA+SVM模型是先通過PCA模型對輸入數據進行降維、特征提取，再通過SVM分類器，對數據進行故障識別，使用網格搜索法對SVM模型參數進行優化，使該模型盡可能達到最優性能。BP神經網絡使用與SAE一樣的網絡結構，通過優化其他超參數，盡可能使BP神經網絡達到最優性能。3種方法均使用同樣的訓練集與測試集，測試不同故障水平下的精度，如圖6所示。

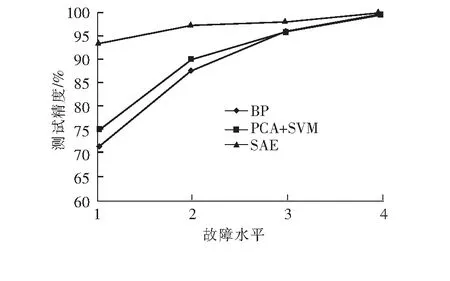
圖6 不同方法在不同故障水平下的測試精度圖

由圖6可知，3種方法在故障水平4的情況下，都顯示出優異的性能(測試精度在99%左右)。但在低故障水平下，SAE的測試精度要高于BP神經網絡與PCA+SVM模型，在該情況下，許多參數與正常運行狀態比較差別不大，PCA本質上是一種線性降維方法，與SAE的非線性降維相比，在提取更深層次的特征信息與處理非線性問題上顯得不足。而BP神經網絡雖然有足夠復雜的網絡結構去學習深層次的特征，但沒有SAE的預訓練過程，容易遇見梯度彌散問題，使得網絡學習效率低下，無法達到理想的效果。SAE神經網絡通過預訓練的方式構造深層神經網絡，自適應地提取特征信息，在故障診斷方面比傳統故障診斷方法更具優勢。