基于GA-BP-AdaBoost強預測模型的大壩變形應用

王 凱,唐詩華,王江波,肖 陽,容 靜，王文貫

(1.桂林理工大學 a.測繪地理信息學院;b.廣西空間信息與測繪重點實驗室,廣西 桂林 541006;2.廣西建設職業技術學院 土木工程系，南寧 530007)

0 引 言

由于大壩變形與多種影響因子密切相關,多元回歸、灰色理論等傳統模型不能很好地預測大壩變形趨勢[1]，學者們總結出了各類模型,如支持向量機模型、神經網絡模型等[2-4]。近來,人工神經網絡特別是BP神經網絡具有自適應、自學習和非線性擬合能力,使得BP神經網絡備受青睞,如高平等[5]將其應用于大壩變形監測,取得了較好的效果。實測數據中將一定會包含隨機擾動誤差,傳統BP神經網絡模型的預測精度會有不同程度的降低。對于神經網絡的缺點,Schapire創建了試圖提升任意給定學習算法精度的普遍方法,即Boosting學習算法,并迅速成了新的學術熱點。AdaBoost(Adaptive Boosting)算法通過迭代弱分類器而獲得最終強分類器，其核心是找到最優的弱分類器[6]。遺傳算法是全局化搜索的,這樣就能夠避開局部極小點, GA-BP遺傳神經網絡把遺傳算法的全局優化和BP神經網絡的局部尋優的特點相結合,在理論上避免了收斂慢、穩定性差和易陷入局部極小值的問題[7],如秦真珍等[8]將GA-BP算法應用于大壩邊坡變形預測,取得了良好的效果;任麗芳等[9]針對深基坑變形問題,將GA-BP模型用于橋梁深基坑變形預測證明預測模型性能良好,精度高,簡便易行;董春旺等[11]先建立BP-AdaBoost神經網絡,然后用遺傳算法尋優求解,將BP-AdaBoost-GA應用于紅茶發酵性能研究并取得了很好的優化效果。

基于上述研究, 提出基于遺傳算法優化BP神經網絡的AdaBoost強預測模型(GA-BP-AdaBoost), 該模型把GA-BP神經網絡作為最優的“弱”預測器, 用遺傳算法進行全局搜索, 進而獲得最優的閾值和權值, 之后再將閾值、 權值向量賦予BP網絡, 利用神經網絡的局部搜索能力獲得網絡的近似最優值。 以GA-BP遺傳神經網絡作為AdaBoost強預測器的“弱”預測器, 利用AdaBoost算法得到強預測器。 結合算例分析表明, 該模型在大壩變形監測中的具有一定的實用性和可行性。

1 GA-BP-AdaBoost強預測模型構建

1.1 AdaBoost強預測理論

Schapire于1990年最早提出了源自Valiant的PAC(probably approximately correct)學習模型的Boosting算法,能提高任意給定學習算法精度。1995年,Freund和Schapire將Boosting算法改進為AdaBoost算法,它們之間效率大致一樣,但不用關于弱學習算法的下限,更容易處理實際問題。AdaBoost算法屬于迭代算法,它是Boosting家族的代表算法,其基本思想是:最終用于決策的強分類器是由不同的弱分類器構成的,而弱分類器則是用同一訓練數據集訓練獲得的。AdaBoost算法具體流程見文獻[6，11]。

1.2 GA-BP遺傳神經網絡

1986年,McCelland等提出了BP神經網絡,它是按照誤差逆傳播算法訓練的多層前饋神經網絡,具有良好的非線性映射能力、容錯和泛化能力[12]。該模型的誤差反向傳播算法的基本過程[13]可以概括為:模式順傳播→誤差逆傳播→記憶訓練→學習收斂。

1962年,Holland提出了遺傳算法(genetic algorithms,GA),它是借鑒生物進化論和自然界遺傳機制而成的[14]。該算法根據所選擇的適應度函數計算各樣本的適應度,經遺傳中的交叉、變異和選擇實現對優秀個體的篩選,新的群體既延續了上一代的信息,又比上一代好[11],使得種群樣本不斷進化,最終獲得全局最優解。

GA-BP遺傳神經網絡在改進的BP神經網絡基礎上,先用遺傳算法進行全局搜索,進而優化BP網絡的閾值和權值,之后將閾值、權值向量賦予BP網絡,利用局部搜索能力得到近似最優值。GA-BP遺傳神經網絡將BP神經網絡的局部尋優和遺傳算法的全局優化特點相結合,保證BP神經網絡收斂于全局最優的同時也能夠得到較為精確的優化結果,在理論上避免了BP易陷入局部極小值、網絡收斂慢和穩定性差的缺點[7]。

1.3 GA-BP-Adaboost強預測模型

GA-BP-AdaBoost強預測模型使用遺傳算法改進的BP神經網絡為弱分類器、利用AdaBoost算法的思想將同一訓練樣本重復訓練GA-BP遺傳神經網絡預測樣本輸出,把多個GA-BP遺傳神經網絡弱預測器用AdaBoost算法獲取組成強預測器。GA-BP-AdaBoost強預測模型步驟如下:

① 數據預處理和網絡初始化。對原始數據進行包含數據和量化歸一化的預處理。從樣本空間中選擇m組訓練數據,初始化測試數據的分布權值Dt(i)=1/m,神經網絡的隱含層節點數的確定到目前仍未找到比較好的解析式來解決[15]。本文用Kolmogorov定理設定隱含層節點數為2q+1，其中q為輸入層節點個數。

② 遺傳算法優化BP神經網絡。將BP神經網絡的閾值和權值當作遺傳算法的染色體,適應度函數用訓練數據訓練BP神經網絡,把預測誤差和當作個體適應度值。

③ 尋找弱預測器gt(t=1,2,…,T)。對第t個弱預測器進行訓練時, 將GA-BP遺傳神經網絡用訓練數據訓練并且預測訓練數據輸出,得到關于預測序列g(t)的誤差和et：

(1)

g(t)=≠y。

其中：y為期望分類結果;g(t)為預測分類結果。

④ 計算預測序列權重。 根據預測序列g(t)的預測誤差和et, 推算序列的權重at。

(2)

⑤ 更新權重。 下一輪訓練樣本的權重根據預測序列權重at進行調整

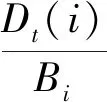
i=1,2,…,m。

(3)

式中:Bt是歸一化因子, 這是為了使分布權值的和為1。 其中

(4)

⑥ 強分類器函數。訓練T輪之后獲得T個弱預測函數gt(x)(t=1,2,…,T), 然后由T個弱預測函數加權組合, 就可以得到一個強預測函數H(x):

(5)

2 算例分析

為了驗證模型的有效性及精度,以某蓄能水電廠的下庫大壩變形監測為例,對位于下庫大壩的河床壩段壩頂的2號觀測點在2000-04-12—2004-06-25這段時間的壩體溫度、水位、時間和大壩Y向變形量進行了63次非等時間間隔觀測,為了方便建立模型,用Hermite插值法把63期非等時間間隔數據調為64期等時間間隔變形數據[3],其變形值如圖1所示。可見,大壩的變形受到多種因素影響,具有較強的隨機性變化,并且呈非線性變化趨勢。

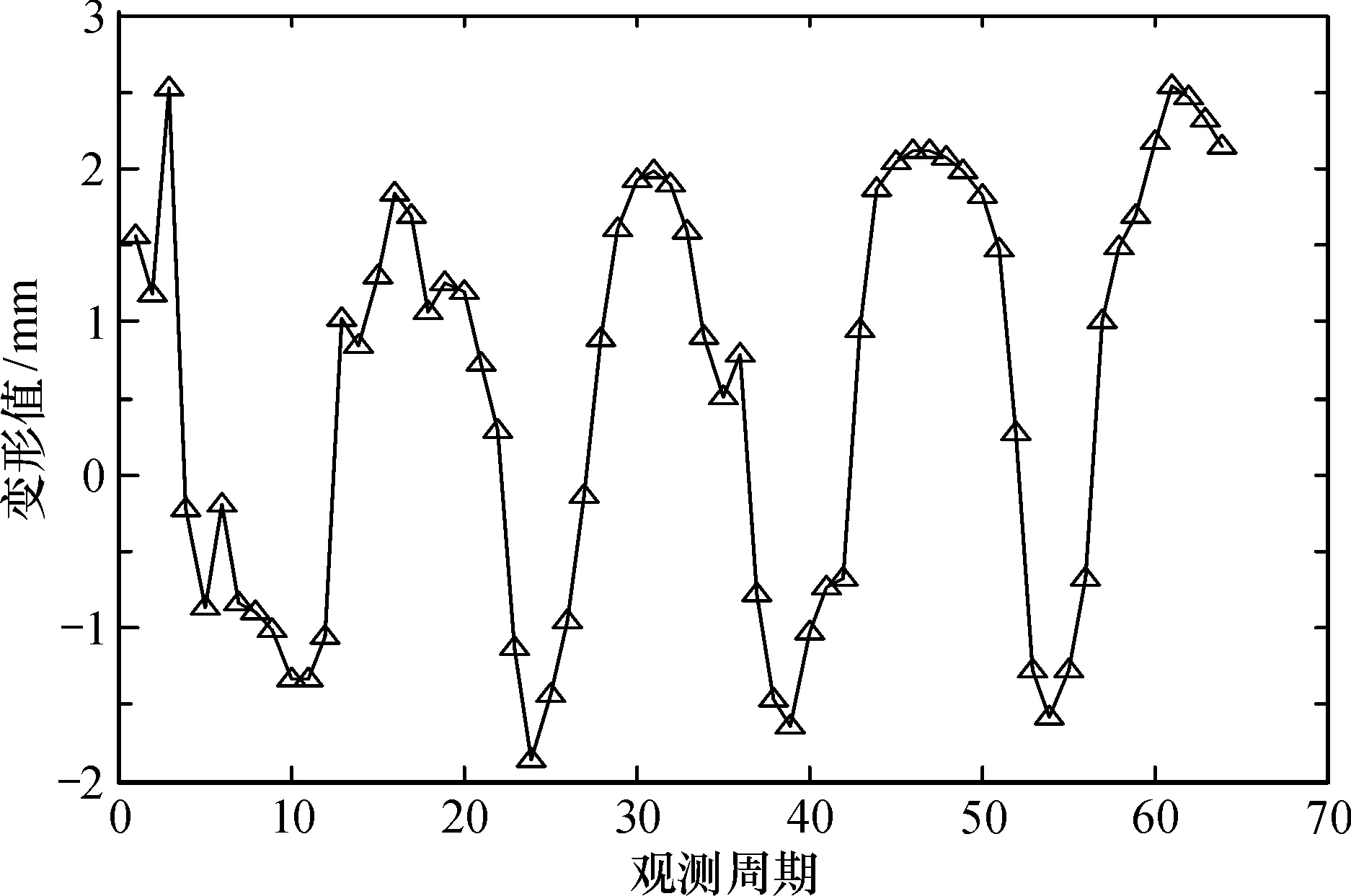
圖1 大壩變形實測值Fig.1 Measured deformation value of dam

擬通過3種方案進行分析:方案1—標準BP神經網絡預測模型，方案2—遺傳BP神經網絡預測模型(GA-BP)和方案3—遺傳算法優化的BP-AdaBoost強預測模型(GA-BP-AdaBoost)。各方案采用了前50期變形觀測數據當作樣本訓練,后14期當作測試樣本。為了方便比較,各方案均采用BP神經網絡標準模型,隱含層和輸入層之間采用Sigmoid函數。各方案BP網絡結構參數具體為:輸入層節點數均為3、輸出層節點數均為1、隱含層節點數均為7,動量項系數和學習率均為0.01,最大循環次數均設置為20。遺傳算法種群范圍設定為10,選擇操作選用輪盤賭法,變異概率和交叉概率分別為0.1和0.3,最大迭代次數均為30。方案1的初始權值和網的連接權值由模型中的代碼隨機生成,而方案2和3,利用遺傳算法優化BP神經網絡。通過對這3個方案模型在大壩變形數據中的預測精度分析,探討各種模型的預測性能,并驗證GA-BP-AdaBoost強預測模型的可行性與優越性。采用平均絕對值、均方根誤差和平均百分比誤差來評定各模型預測精度:

1) 平均絕對誤差(MAE)

(6)

2) 均方根誤差(RMSE)

(7)

3) 平均絕對百分比誤差(MAPE)

(8)

用大壩監測原始數據輸入各模型來訓練, 獲得預測輸出值。 各方案模型的計算結果對比見表1。

表1 各模型計算結果

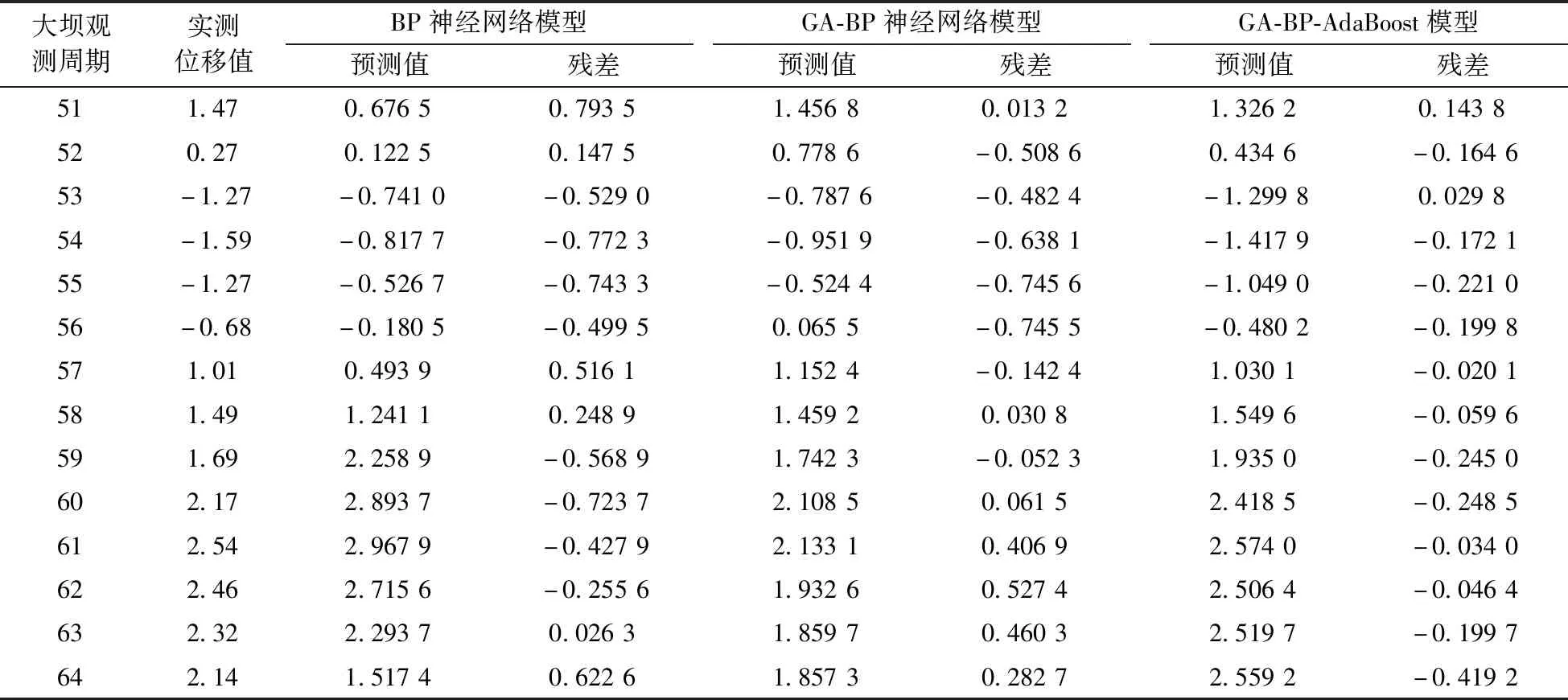
Table 1 Contrast of each model calculation results mm

可見,方案1的標準BP神經網絡預測模型的殘差很大,模型殘差序列絕對值超過0.6 mm的有5期,最大殘差達到0.793 5 mm,方案2 GA-BP神經網絡模型的預測殘差序列絕對值超過0.6 mm的有3期,最大殘差達到-0.745 6 mm,說明遺傳算法優化的BP神經網絡模型在大壩變形預測精度上較標準BP神經網絡有了很大幅度的改進,遺傳算法最終訓練結束時還是由期望輸出目標決定的,雖然算法運行速度得到了提升,但是預測精度并沒有顯著提高。方案3 GA-BP-AdaBoost強預測模型的預測殘差序列除最大殘差外,其余各期均低于0.3 mm,而最大殘差為-0.419 2 mm。表明該模型在大壩變形預測精度上較方案1和2有了大幅提升。

從各模型變形預測值和實際變形值對比(圖2)可知,方案1和方案2在大壩變形預測段的前期和中期,兩者的變形趨勢基本一致且預測值相差不大,在后期兩者出現背離。方案3GA-BP-AdaBoost模型預測值在整體變化趨勢上與大壩實際變形值相一致,且兩者之間的差值相比方案1和方案2很小,表明方案3可以很好地預測大壩變形趨勢。

圖2 各模型預測值和實際值對比Fig.2 Comparison of predicted and actual values of each model

由殘差圖(圖3)可知,方案1的殘差波動范圍最大,方案2較方案1波動范圍有所減小,而方案3的殘差波動范圍幾乎穩定在0.2 mm以內。表明GA-BP-AdaBoost強預測模型具有很高的全局預測精度,且預測性能較為穩定。

為進一步綜合評定各種模型的性能,采用均方根誤差、平均絕對誤差和平均絕對百分比誤差3項指標進行評定,各預測模型的精度指標計算見表2。

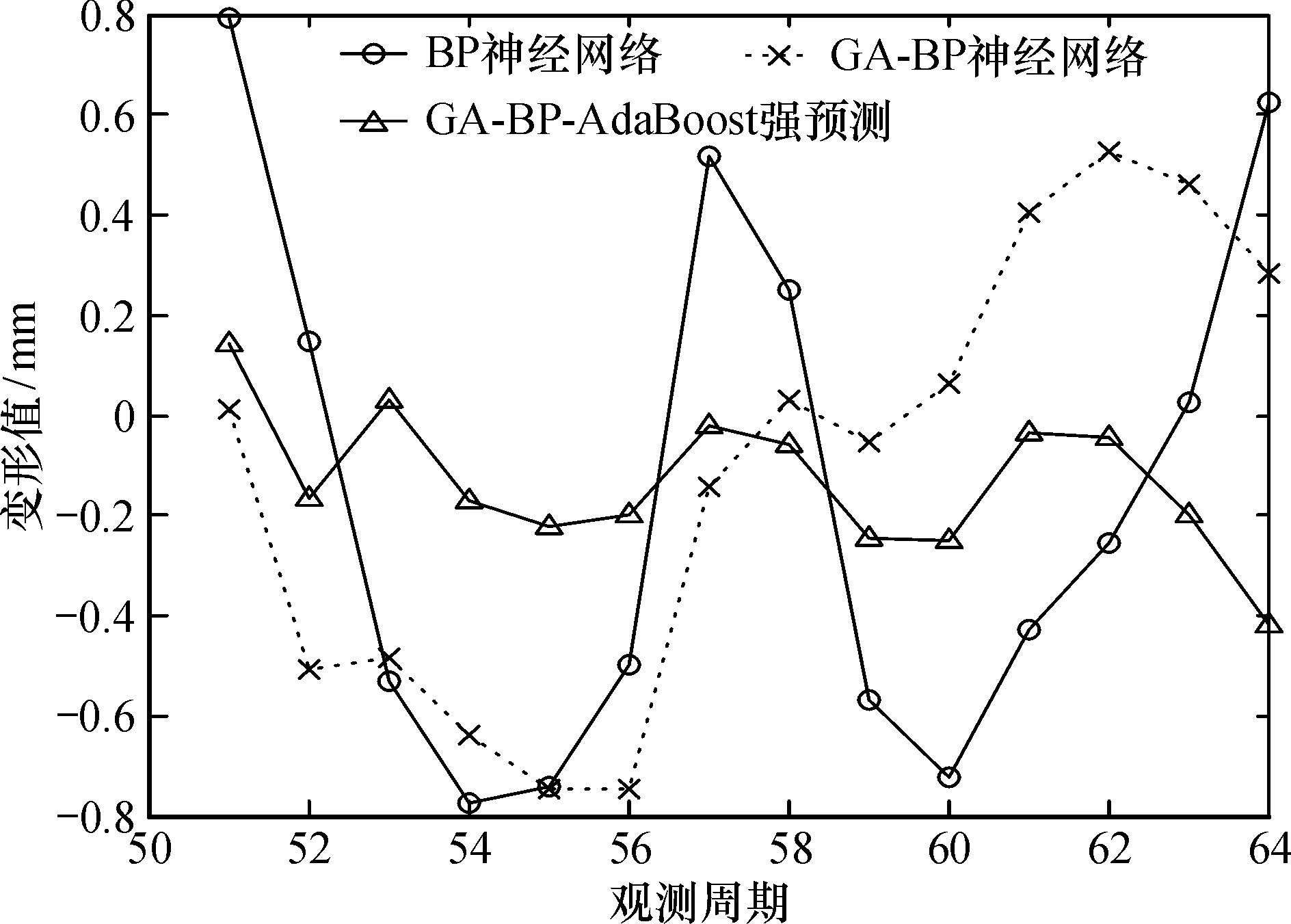
圖3 各模型殘差對比Fig.3 Residual comparison of models

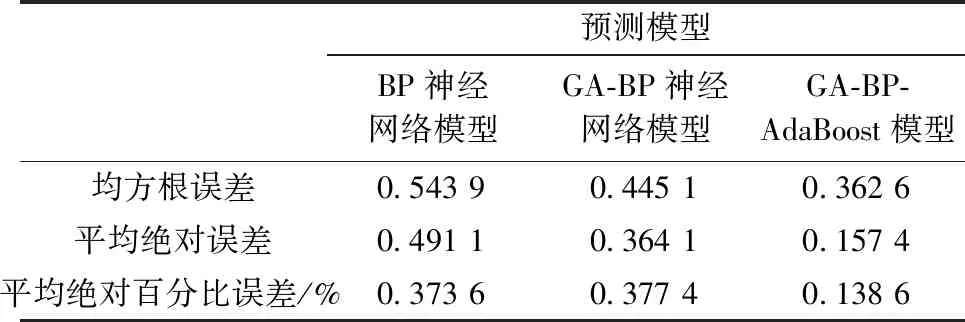
Table 2 Contrast of precision of each model mm

對各模型的預測精度而言, 方案1較方案2在均方根誤差和平均絕對誤差指標方面, 精度略低, 分別為0.543 9和0.491 1 mm, 但是兩者在平均絕對百分比誤差方面精度幾乎一樣, 反而標準BP神經網絡稍高于GA-BP遺傳神經網絡模型, 說明遺傳算法對于BP神經網絡預測模型的精度提高有限。方案3 GA-BP-AdaBoost強預測模型各項精度指標在3種模型中均是最小的,分別為0.362 6 mm、0.157 4 mm、0.138 6%,這表明,AdaBoost強預測器根據預測誤差調整若干組弱預測器之間的權重,能夠把遺傳算法隨機選擇交叉、變異優化后的BP神經網絡不同的預測結果綜合起來,實現AdaBoost強預測器“優中選優”的目標,最大限度地提高了模型預測精度的同時也驗證了提出的基于遺傳算法優化的BP-AdaBoost強預測模型在大壩變形監測中的優越性和可行性。

3 結束語

經理論和算例分析,并與標準BP神經網絡模型、GA-BP遺傳神經網絡模型對比表明,標準BP神經網絡模型由于要設定適宜的模型參數,并且初始閾值和權值是系統任意給定的,具有不確定性的預測結果;GA-BP遺傳神經網絡模型雖用遺傳算法經由隨機選擇變異、交叉優化了BP神經網絡的權值和閾值,彌補了BP神經網絡容易陷入誤差函數的局部極值點的缺陷,在預測精度上有了一定程度的提高,最終閾值和權值仍由期望輸出目標決定的,預測精度和穩定性仍待提高;而GA-BP-AdaBoost強預測模型的弱預測器同時融合了遺傳算法全局優化和BP神經網絡的局部尋優特點,同時AdaBoost強預測器能夠通過給弱預測器的若干預測序列賦予不同的權重,綜合了不同預測序列的優勢,實現了AdaBoost強預測器“優中選優”的目標,最大限度的提升了預測精度,證實了提出的基于GA-BP-AdaBoost強預測模型在大壩變形監測中的可行性和實用性。通常GA-BP-AdaBoost強預測模型更加適合非線性模型,但針對一些因為樣本數量小、樣本分布不均勻而造成神經網絡預測誤差大的問題,還有待后續進一步研究。