某隧道牽引電流及鋼軌電位分布測試與仿真研究

王保松，喬胤瑋

(1.中國鐵路太原局集團有限公司大同電務段，山西大同 036200；2.石家莊鐵道大學，石家莊 050043)

1 概述

某隧道位于AB 兩站之間，是兩座獨立的單線隧道，因隧道內電力設備老化，導致鋼軌對地電位升高，實測值最大可達285 V。在現場的使用中，牽引回流對鋼軌對地電位的影響會使軌道旁信號電纜芯線產生干擾，同時對鋼軌行駛機車的安全性產生不良影響。另外，當對列車軌道進行日常檢修時，其存在的鋼軌電位問題也會影響工作人員的人身安全。為解決這些問題，應該采用可行的措施，盡可能降低鐵道鋼軌上的對地電位[1]。

某隧道列車供電采用直供帶回流方式，直供電壓為27.5 kV。隧道的上下行線路均由某牽引變電所的單個供電臂供電，上下行線路分別由2#主變壓器的214/213 支路供電。供電臂上下行起止位置坐標分別為：上行K159+327 ～K179+915，下行K159+294 ～K179+521。

2 牽引供電系統的建模

牽引供電系統的模型主要包括3 大部分：牽引變電所、牽引網、電力機車。在不考慮運行工況時，可以將電力機車視為理想電流源模型。

牽引變電所的外部接入三相110 kV 供電系統，所內安裝的是110/27.5 kV 的Vv 接線牽引變壓器。

大地、綜合地線、鋼軌、保護線、承力索、接觸線和正饋線所組成的供電網絡總稱為牽引網[2]。牽引網可以用多導體傳輸線來描述，各導體傳輸線除有自阻抗外，它們之間還存在互阻抗。

當電氣化鐵道通過長大隧道時，牽引網四周的大地結構與橋箱、路基是不一樣的，隧道中導線阻抗用Carson 公式計算，必然帶來誤差影響，需要采用Tylavsky 公式計算隧道中導線阻抗，它是適用于大地圓形隧道模型的[3]。

2.1 某隧道牽引供電系統概述

2.1.1 牽引網的結構

隧道內供電牽引網系統裝置為剛性懸掛，形式為曲臂連接。

剛性懸掛梁的結構為“Π”型，其匯流排型號為PAC110，橫截面積為0.221 4 cm2，銅當量截面為0.118 1 cm2，具有3 500 A 以上載流能力[4]。接觸線材質為銀銅合金，導線橫截面積為0.012 cm2，導線距鋼軌為6.35 m。

隧道外的接觸網結構與隧道內不同，其裝置方式為柔性懸掛。

牽引供電系統設計規范要求平均每隔1.5 km設置1 條吸上線，隧道內吸上線的具體位置分布如表1 所示。

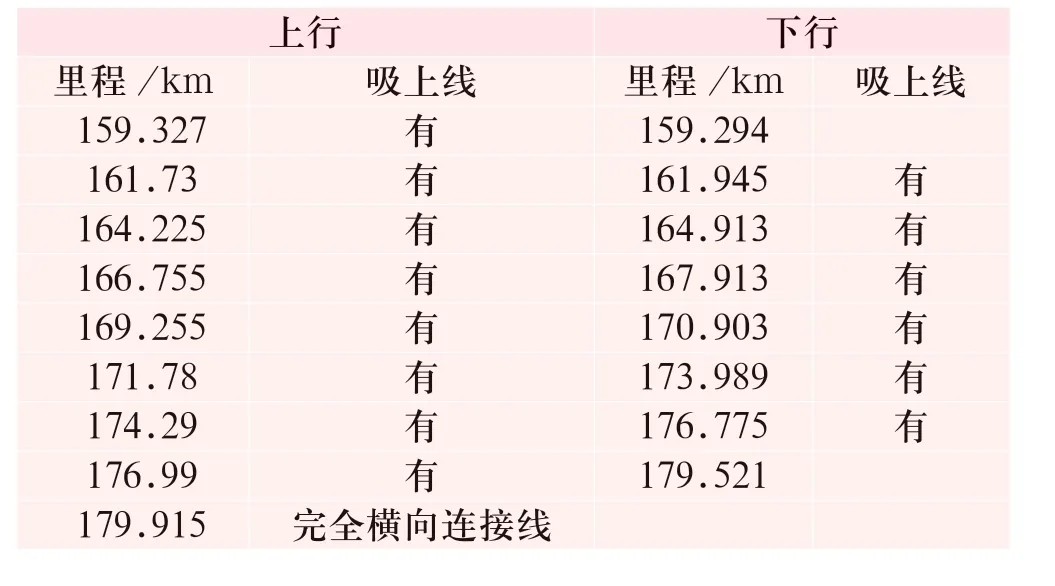
表1 吸上線的位置分布Tab.1 Location distribution of boosting cable

2.1.2 模型參數計算

依據牽引網等效阻抗計算公式的需求，整理得到某隧道內外各導線的坐標如表2、3 所示，導線線材及其電氣參數如表4 所示。

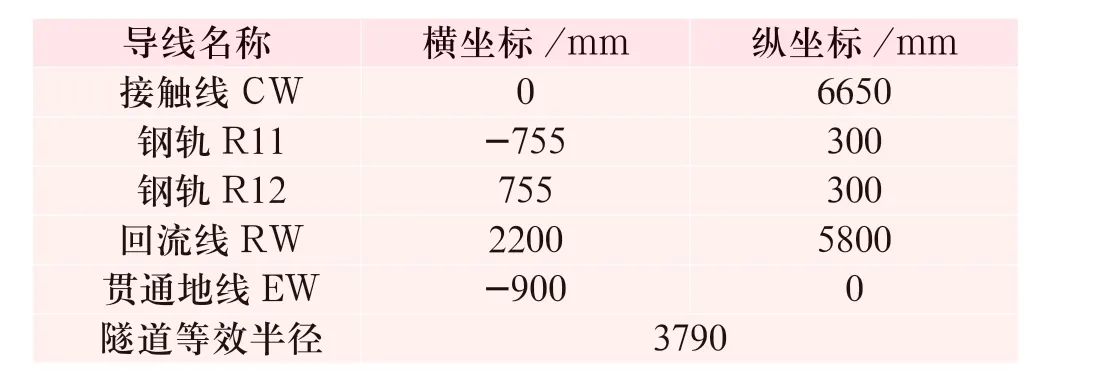
表2 隧道內各導線坐標Tab.2 Coordinates of wires in tunnel

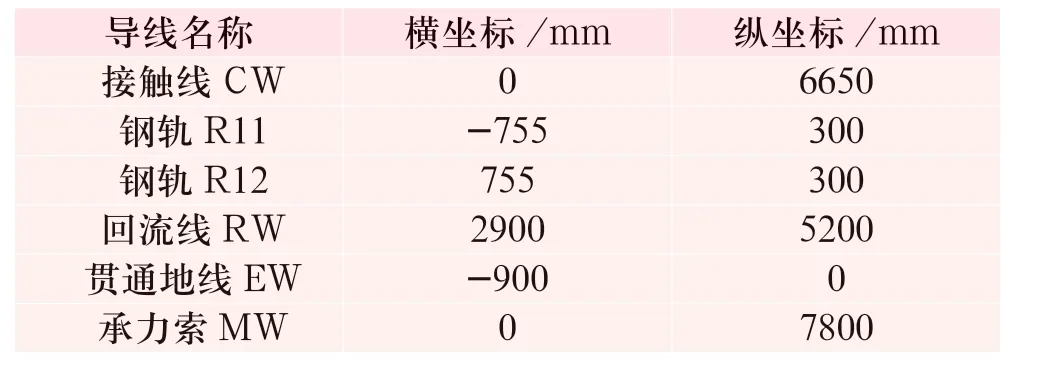
表3 隧道外各導線坐標Tab.3 Coordinates of wires out of tunnel

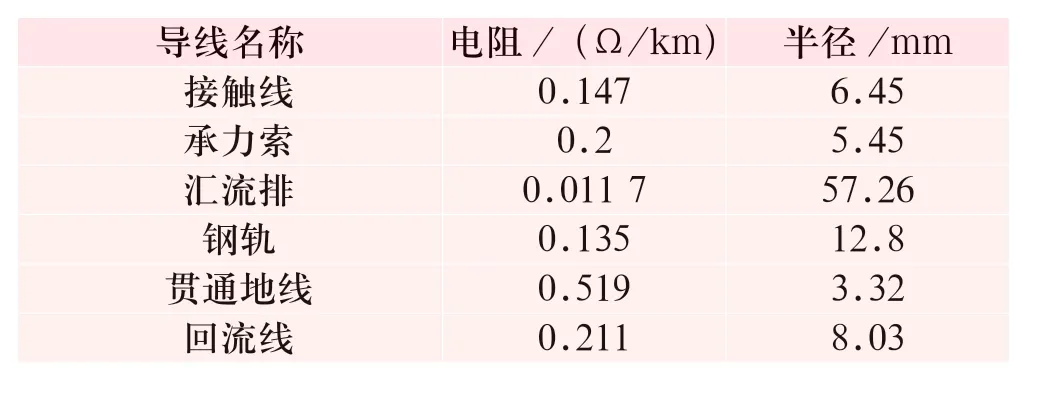
表4 各導線電氣及物理參數Tab.4 Electrical and physical parameters of wires

假設上下行隧道相距20 m，且隧道內導線的位置成鏡面對稱，利用自阻抗和互阻抗的計算公式，可以計算得到隧道內、外牽引網的電阻和電抗矩陣。

在Simulink 中，將計算得到的電阻矩陣和電抗矩陣輸入Mutual Inductance 模塊，可以實現對牽引網的建模。另外，貫通地線和鋼軌對大地的漏泄，直接利用接地電阻來模擬。

3 隧道內測試實驗

3.1 測試內容

測試實驗在軌旁共設置3 個測試點，從3 月22日至24 日進行3 天的數據采集。3 個測試點的具體情況如下。

采集點1：位于1605G 兩吸上線中間位置K160+260 處，此處位于下行隧道的入口，現場在靠近A 站方向的隧道口處裝置人工接地網，其電阻值小于1 Ω，采集此處軌面電壓和貫通地線中電流。

采集點2：位于1649G 靠近A 站側吸上線位置K164+913 處，此處位于下行隧道的中部，采集此處軌面電壓、吸上線電流和貫通地線電流。

采集點3：位于1649G 兩吸上線中間位置K166+200 處，此處位于下行隧道中部，采集此處軌面電壓和貫通地線電流。

調閱該隧道區段測試時間段內列車的運行時刻以及牽引變電所內饋線電流與主變軌地回流情況，確定測試時測試區段上的行車情況，包括區段內列車的數量、牽引電流大小以及軌地回流大小。

3.1.1 算例分析

通過查閱和分析列車運行時刻和饋線電流，選取3 組列車通過隧道區段的詳細工況，包括時間、測試點、機車位置以及機車電流信息，如表5 所示。

表5 列車通過隧道區段的詳細信息Tab.5 Details of trains passing through the tunnel section

利用第2 節建立的系統仿真模型，分別計算如表5 所示的工況，對比仿真和實測實驗的結果，如表6、7、8 所示。

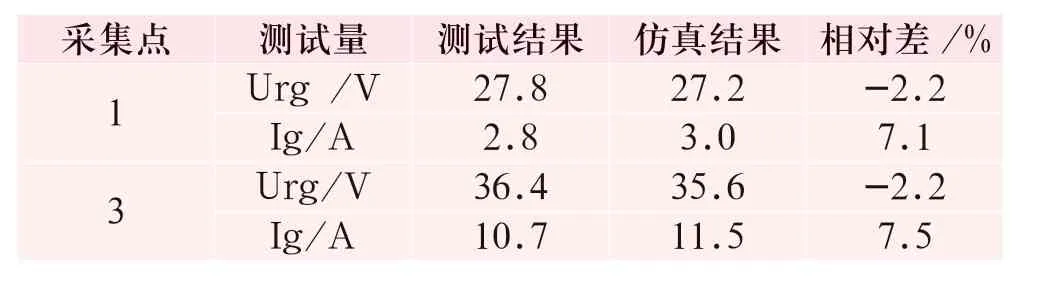
表6 22nd 02：45實測數據和仿真結果對比Tab.6 Comparison between the measured data and simulation results at 02:45 on 22nd

表7 23rd 03：05實測數據和仿真結果對比Tab.7 Comparison between the measured data and simulation results at 03:05 on 23rd

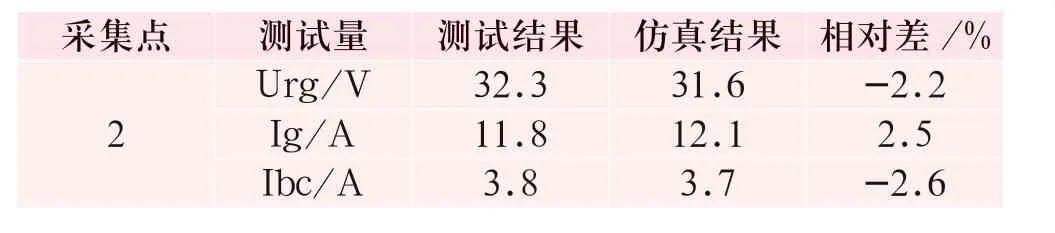
表8 24th 02：55實測數據和仿真結果對比Tab.8 Comparison between the measured data and simulation results at 02:55 on 24th

從表6、7、8 中可以看出，同一時刻同一位置上，Ig 的仿真結果要高于測試結果，對應的Urg和Ibc 卻低于測試結果，主要原因是在仿真計算中分布式的對地雜散電流通過集中式的阻抗來模擬。但是仿真結果和測試結果的相對差較小，最大為8.0%，因此可以認為該模型是正確的。

3.2 探究對地電位的影響因素

3.2.1 完全橫向連接線的影響

以22 日02:45 的運行工況為例，仿真末端回流網末端存在或不存在完全橫向連接時，不同鋼軌對地電阻值下，測試點3 的貫通地線電流I、軌面電壓V以及對地電位V0，仿真結果分別如圖1、2 所示。

從圖1 中可以看出，存在完全橫向連接線時，隨著鋼軌對地電阻的增大，貫通地線中的電流值呈減小趨勢，且變化幅度較小。軌面電壓和對地電位的大小隨著鋼軌對地電阻值的增加，呈現相反的變化趨勢。

對比圖1、2，不存在完全橫向連接線時，同一仿真結果的變化趨勢和存在時的大致相同。隨著對地電阻值的增大，對地電位增大到一定值后，不再升高，主要是由于貫通線的存在使電位不再增大。但不存在橫向連接線時電流的變化幅度更大，同一大地電阻率值下對地電位的最大值也更大，如圖3 所示，因此末端設置完全橫向連接線有利于降低鋼軌對地電位。

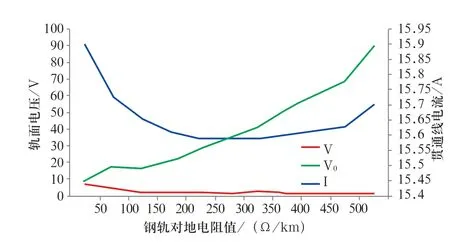
圖1 末端存在完全橫向連接時，不同鋼軌對地電阻時測試點3的仿真結果Fig.1 Simulation results of test point 3 with different rails resistance to ground when there is a complete cross connection at the end

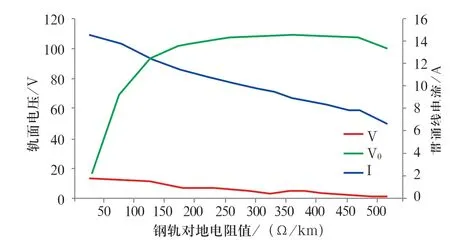
圖2 末端不存在完全橫向連接時，不同鋼軌對地電阻時測試點3的仿真結果Fig.2 Simulation results of test point 3 with different rail resistance ground when there is no complete cross connection at the end

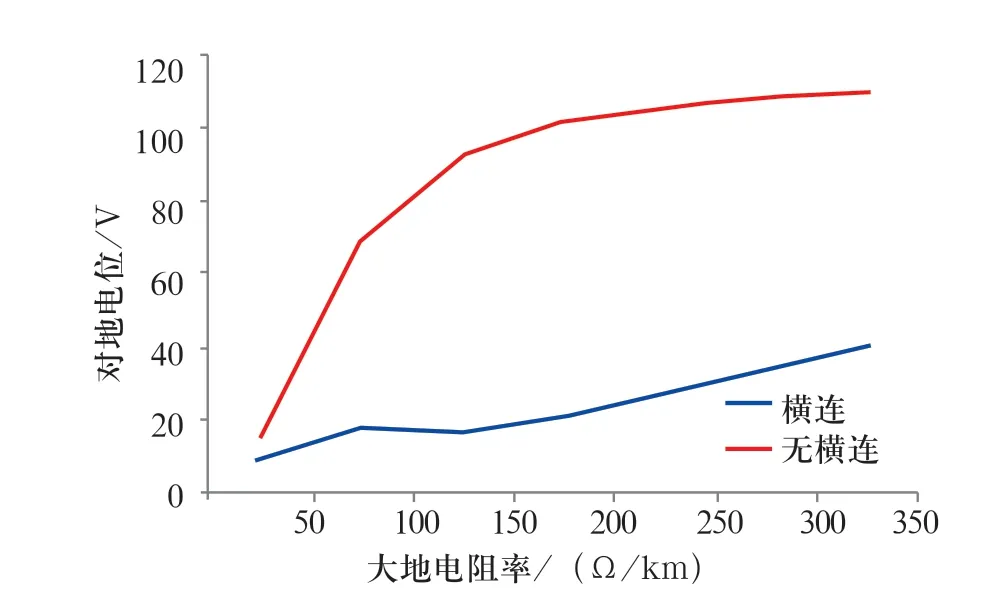
圖3 末端不同橫向連接時，鋼軌對地電位隨大地電阻率的變化Fig.3 Variation of rail potential to ground with earth resistivity when different ends are connected horizontally

3.2.2 貫通地線的影響

以22 日02:45 的運行工況為例，為考慮EW線的影響因素，對比選用橫截面積為70 mm2和35 mm2的貫通地線時，末端存在橫向連接和不存在橫向連接時，不同大地電阻率下鋼軌對地電位的變化，對比結果如圖4 所示（橫連-35 和橫連-70 指存在橫向連接時EW 線不同截面積的情況，無橫連-35 和無橫連-70 指不存在橫向連接時EW 線不同截面積情況）。

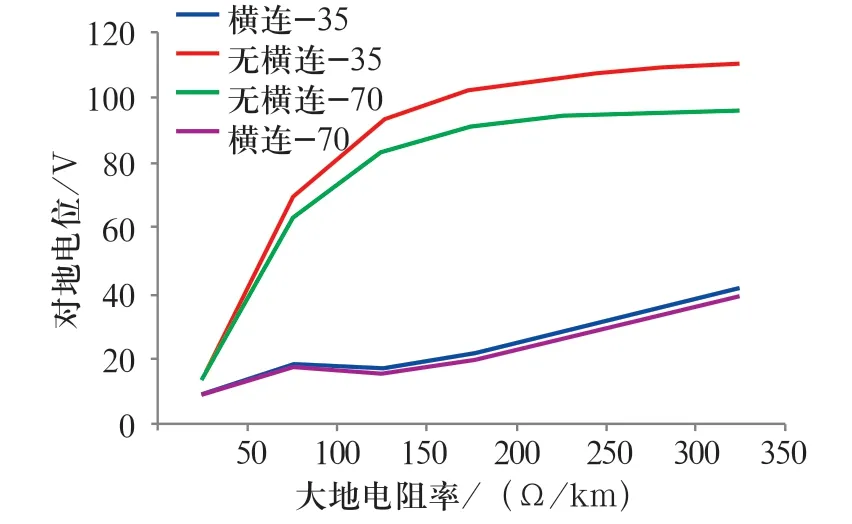
圖4 鋼軌對地電位隨大地電阻率變化的對比Fig.4 Comparison of variation of rail potential to ground with earth resistivity

從圖4 可以看出，采用截面積大的貫通地線，鋼軌對地電位較小。不存在完全橫向連接線時，軌道對地電位的變化更大。

對比存在和不存在橫向連接線的情況下，采用2 根間隔0.5 m 的35 mm2的貫通地線和1 根70 mm2的貫通地線時，鋼軌對地電位隨大地電阻率的變化，結果分別如圖5、6 所示。

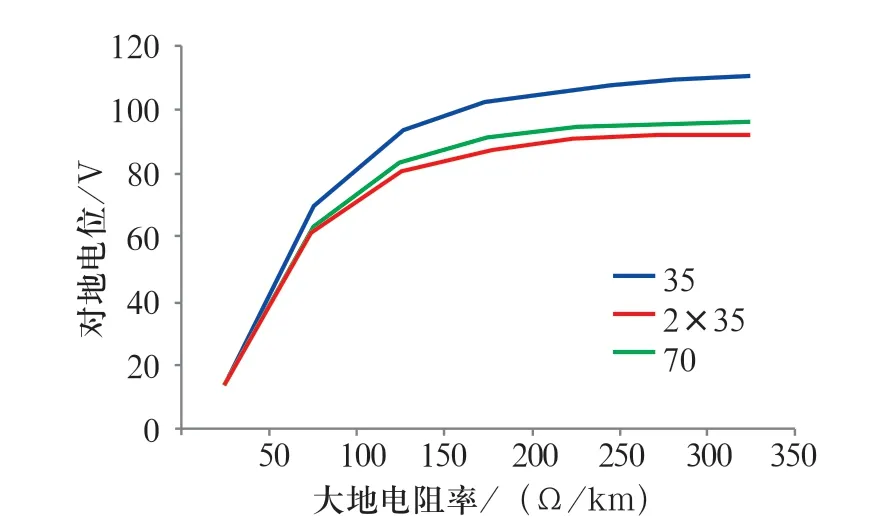
圖5 不存在橫連線情況下，采用不同貫通線時，鋼軌對地電位隨大地電阻率變化的對比Fig.5 Comparison of variation of rail potential to ground with earth resistivity when different through lines are used without cross connection

從圖5、6 中可以看出，無論是否采用橫向連接線，采用2 根35 mm2的貫通地線時，同一大地電阻率下同一地點鋼軌對電位比1 根70 mm2的貫通地線時鋼軌對地電位要小，與大地電阻率呈正相關。

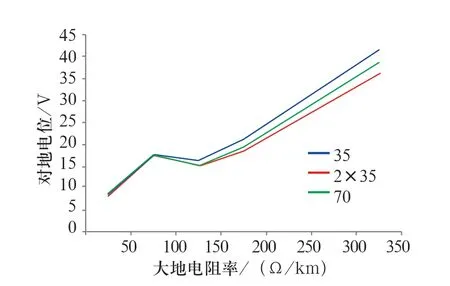
圖6 存在橫連線情況下，采用不同貫通線時，鋼軌對地電位隨大地電阻率變化的對比Fig.6 Comparison of variation of rail potential to ground with earth resistivity when different through lines are used in the case of cross connection

若探究2 根貫通地線間距分別為0.1、0.5 和1 m，從仿真分析可以看出，間距的變化對鋼軌電位的干擾較小。

3.2.3 回流線的影響

考慮單雙回流線的情況，從圖7 對比可以看出，無論是否存在橫向連接線，同一大地電阻率雙回流線時的鋼軌對地電位都要小于單回流線的值。

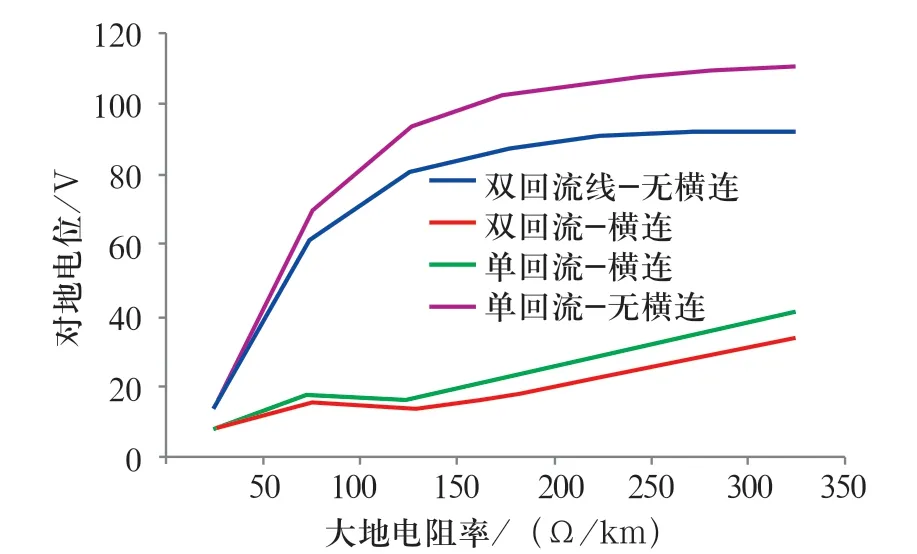
圖7 單雙回流線時鋼軌對地電位隨大地電阻率變化的對比Fig.7 Comparison of variation of rail potential to ground with earth resistivity in case single and double return lines

4 結論

以某隧道區段的牽引供電系統為例，將仿真結果和實際測試結果進行對比，在參數和牽引網結構確定時，兩者的結果基本相符。該仿真模型可以推廣到其他直供帶回流的牽引供電系統中，實現牽引回流以及鋼軌對地電位分布的仿真計算，為設計新線和改造列車供電系統提供相關的理論支撐。通過研究完全橫向連接線設置、貫通地線以及回流線的各種影響因素，最后得出末端設置完全橫向連接線，設置雙貫通地線或者雙回流線都可以有效降低鋼軌對地電位。