SAW式WTP輸入及輸出阻抗匹配研究

劉守兵，盧文科

(1.河南工程學院 電氣信息工程學院，河南 鄭州 451191；2.東華大學 信息科學與技術學院,上海 201620)

0 引言

聲電式小波變換處理器(WTP)，特別是聲表面波(SAW)式WTP不但能對信號進行小波變換[1]，且還具有獨有的體積小，結構簡單和性能可靠等優點[2]，因而其在氣體檢測、水位測量、雷達目標識別等領域得到廣泛的應用[3-6]。為此，研究人員設計了一系列性能優良的SAW式WTP[7-8]。但是，組成這些SAW式WTP的叉指換能器(IDT)的等效電路是一個三端口網絡，其插入損耗和三次渡越反射都與輸入、輸出阻抗有關[9]。若直接將該芯片用于電子系統中，受三次渡越反射的影響，其通帶將會產生波紋，進而將該波紋引入轉換后的信號中。為此，必須對SAW式WTP的輸入、輸出阻抗匹配進行研究。

求取SAW式WTP的輸入、輸出阻抗的方法很多，但大多需要借助測量器具實現[9]。為此，本文擬采用導納矩陣來求取其輸入、輸出阻抗，進而由其設計相應的匹配網絡。采用這種方法求取SAW式WTP的輸入、輸出阻抗，必須先求出該器件的導納矩陣。但現有的導納矩陣計算方法由于只能求取兩IDT都未加權的SAW器件的導納矩陣，而無法將其直接用于一個IDT加權的SAW式WTP的導納矩陣[10]。為此，本文引入了通道分割法[11]，將一個IDT加權的SAW式WTP轉換成一系列可等效為兩IDT均未加權的SAW器件的平行通道，進而由每個通道的導納矩陣求取整個SAW式WTP的導納矩陣，并由其求取該器件的輸入、輸出阻抗，設計其匹配網絡。

1 SAW式WTP的原理與設計

Morlet小波函數的時域表達式[12]為

(1)

式中：s為小波函數的尺度；f0為其中心頻率；t為時間。

根據式(1)，小波函數的包絡函數[13]為

(2)

經過大量的研究[14-15]可發現，如果按照式(2)設計SAW器件的輸入IDT指條重疊包絡，而輸出IDT采用指條相等重疊、均勻周期的電極結構，就可以設計出一個SAW式WTP。

根據式(2), SAW式WTP的聲孔徑長度為

(3)

式中:n為指條編號;k為聲孔徑長度與對應包絡值比值的常數。

2 SAW式WTP的導納矩陣

2.1 兩IDT均為加權的SAW器件的導納矩陣

SAW器件在電子系統中應用時的連接示意圖如圖1所示。將1個內阻抗為Zs的電壓源(Vin)連接到輸入IDT上，負載ZL連接到輸出IDT上。從電信號傳輸的角度來看，該器件可等效為1個信號變換器件，可用二端口網絡表示，則有

I1=y11V1+y12V2

(4)

I2=y21V1+y22V2

(5)

式中:y11、y12、y21和y22為該二端口網絡的導納參數;V1、I1、V2、I2分別為輸入電壓、輸入電流、輸出電壓、輸出電流。

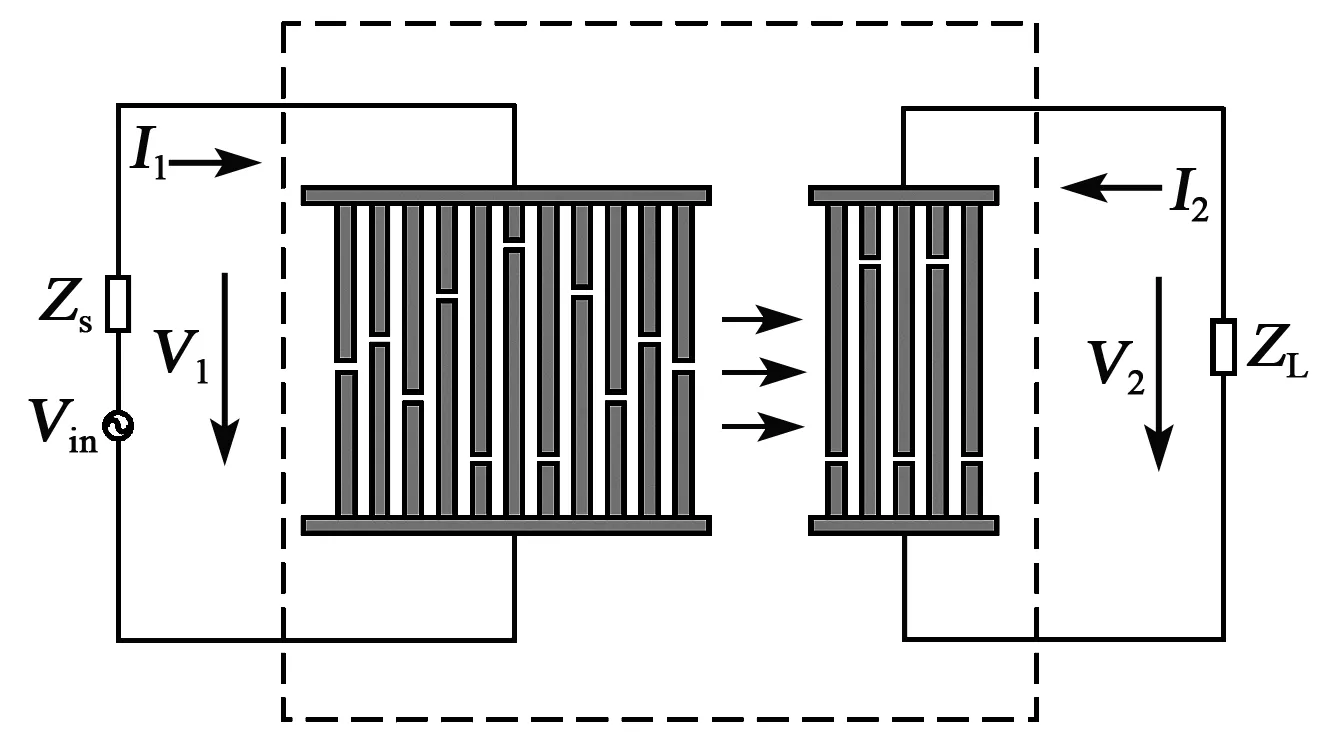
圖1 SAW器件的等效二端口網絡

對于兩個IDT都未加權的SAW器件，這些導納參數可通過下式計算：

(6)

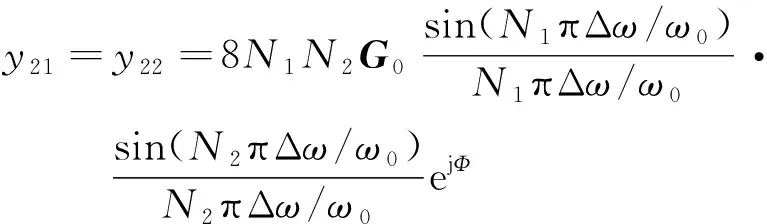
(7)

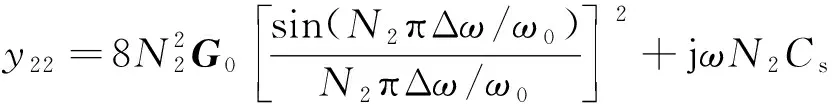
(8)

式中：N1為輸入IDT的指對數；N2為輸出IDT的指對數；G0=ω0CsK2/(2π)為SAW器件的特性導納矩陣，K2為基片材料的機電耦合系數；ω0=2πvs/L為聲同步角頻率，vs為SAW在基片材料自由表面的傳播速度，L為1個叉指周期的長度；Cs為一對叉指的靜態電容；Δω=ω-ω0和Φ為由兩IDT的中心距造成的相位角；j表示該部分為復數的虛部。

根據式(4)～(8)即可得到SAW器件的導納矩陣為

(9)

2.2 SAW式WTP的導納矩陣

由于SAW式WTP的輸入IDT采用切趾加權的電極結構(見圖2)，因而我們無法直接采用式(6)～(9)計算出該器件的導納矩陣。為此，我們引入Tancrell 和Holland兩位學者首創的通道分割法，并通過這種方法將SAW式WTP分割成一系列平行的通道，如圖2所示。圖2中，通道由水平折線標識，而通道邊緣由電極邊緣標識。每個通道都可以看作是一個兩IDT均未加權的SAW器件，從而可以利用式(6)～(9)求出每個通道的二端導納矩陣。

圖2 SAW式WTP的結構示意圖

若一個SAW式WTP的輸入IDT的指條對數為Nsr，輸出IDT的指條對數為Nsc，根據圖2，并經適當的數學推導，可得到以下結論:

該SAW式WTP可分割的平行通道個數為

Ntd=Nsr

(10)

當通道個數Ntd為奇數時：

對于每個通道，其輸入IDT的指條對數為

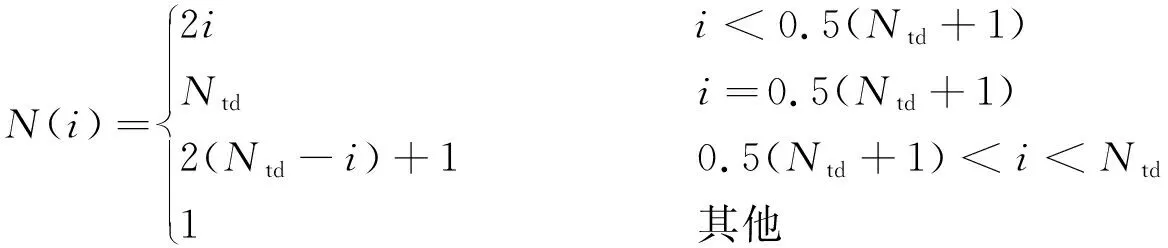
(11)

式中i為通道編號。

對于每個通道，其聲孔徑長度為

(12)

式中Li為SAW式WTP輸入IDT中編號為i的指條重疊包絡的長度。

當Ntd為偶數時：

對于每個通道，其輸入IDT的指條對數為

4.自動駕駛功能駕駛員有不當適用，但駕駛員駕駛或操作沒有過錯，也沒有違反道路交通安全法律法規，此種情況下交通肇事的法律責任由自動駕駛功能的制造商或供應商承擔責任；

(13)

對于每個通道，其聲孔徑長度為

(14)

若周期段內單位長度指條的靜態電容為C0，則由式(12)、(14)可計算出一對叉指的靜態電容為

Cs(i)=C0W(i)

(15)

將式(11)、(13)和(15)代入式(6)、(7)和(8)中，即可得到每個通道的導納矩陣。

依據二端口網絡的簡化原則，可求得整個SAW式WTP的導納矩陣為

(16)

3 SAW式WTP的輸入及輸出阻抗匹配

綜上所述可知，SAW式WTP可等效為一個二端口網絡，且已算出該二端口網絡的導納矩陣。根據二端口網絡的性質，由SAW式WTP的導納矩陣可計算出其輸入、輸出阻抗為

(17)

(18)

式中conj(·)為共軛運算。

利用式(17)、(18)求取的輸入、輸出阻抗即可設計出SAW式WTP的匹配網絡。

4 方案論證與討論

為了驗證本文提出的SAW式WTP的輸入、輸出阻抗匹配方案，本文專門設計了SAW式WTP的參數如表1所示。表中ε∞為介電常數。

表1 SAW式WTP的設計參數

根據式(3)可設計出上述SAW式WTP，并得到該器件的Nsr和每根指條的Li，進而可由式(10)～(15)算出該SAW式WTP分割的平行通道數Ntd，每個通道內輸入IDT的指條對數N(i)和一對叉指的靜態電容Cs(i)。由這些參數利用式(6)～(8)計算出每個通道的導納矩陣Yi，進而可由式(16)計算出整個SAW式WTP的導納矩陣，即

(19)

與此同時，我們還實際制作了SAW式WTP，并利用文獻[4]提供的方法實際測量了該器件的導納矩陣，則有

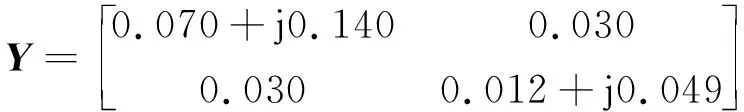
(20)

對比式(19)、(20)可知，理論計算的導納矩陣與實測的導納矩陣相比，其誤差基本可忽略，能滿足理論研究和應用的精度要求。

將式(19)代入式(17)、(18)，即可得到該SAW式WTP的輸入、輸出阻抗為

Zs=3.209+j5.553

(21)

ZL=3.090+j17.305

(22)

利用式(21)、(22)可設計出該器件的匹配網絡。

采用文獻[16]可測量出匹配前、后的SAW式WTP的插入損耗分別為31.6 dB和19.2 dB，降低了39.2%。

5 結束語

本文對SAW式WTP的輸入、輸出阻抗匹配進行了研究。為了求取匹配網絡中需要的輸入、輸出阻抗，本文首先根據通道分割法將SAW式WTP分割成一系列可等效為兩IDT都未加權的SAW器件的平行通道，并首次給出通道數、各通道輸入IDT的指條對數和一對叉指的靜態電容；然后根據這些參數計算出各個通道的導納矩陣和整個SAW式WTP的導納矩陣；最后根據這個導納矩陣計算出該器件的輸入、輸出阻抗，并對該阻抗的SAW式WTP的插入損耗的影響進行了驗證。理論研究和實驗結果表明，利用這種方法設計的SAW式WTP的匹配網絡，可以使該器件的插入損耗降低30%以上，因而其具有顯著的理論意義和應用價值。