橡膠壩壩體振動模態特性及防治措施
任鐘剛
(菏澤市黃淮水利設計咨詢有限公司,山東 菏澤 274000)
橡膠壩通常采用高強纖維布作為受力骨架,外接硫化橡膠層進行止水后向內沖入氣體或液體,從而形成橡膠柔性擋水體,在我國水利工程尤其是小型水利工程建設中起到不可或缺的作用。本文以山東省某擬建橡膠壩工程為例,通過ANSYS建立流固耦合條件下的橡膠壩壩體模型并進一步分析其振動模態特性與變形破壞特征,以求為該工程的安全建設提供一定的理論依據。
1 流固耦合振動理論及模型建立
1.1 流固耦合振動理論
在不考慮阻尼的基本假設條件下,基于流固耦合理論進行橡膠壩壩體的振動模態分析時,流體對壩體結構作用時的自由振動方程為:
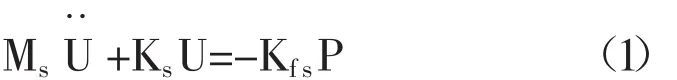
式中:Ms、Ks分別為結構的質量矩陣、剛度矩陣,U為節點位移矩陣,為加速度矩陣,Kfs為剛度矩陣,P為擾動壓強。根據Navier-Stokes方程,可以進一步推出離散條件下結構動力學方程如下:
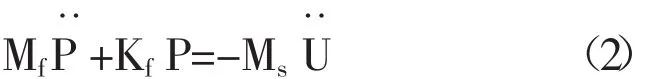
式中:Mf、Kf、Mfs分別為流體的質量矩陣、剛度矩陣及流固耦合質量矩陣。聯合式(1)、(2)得流固耦合條件下系統的完整控制方程如式(3):
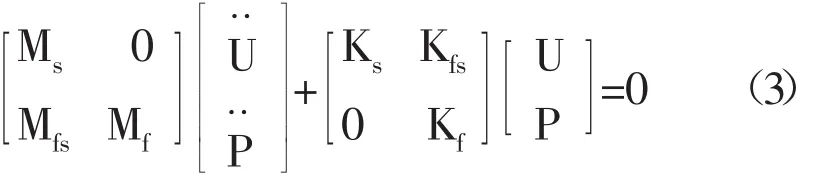
1.2 流固耦合模型建立
根據該橡膠壩工程相關資料及現場調查數據反饋,擬建橡膠壩尺寸為5.00m×15.18m,壩體及水體具體材料參數如表1所示。根據上述數據建立基于流固耦合理論的橡膠壩振動模態分析模型,壩體采用殼體單元SHELL63,水流采用流體單元fluid30。
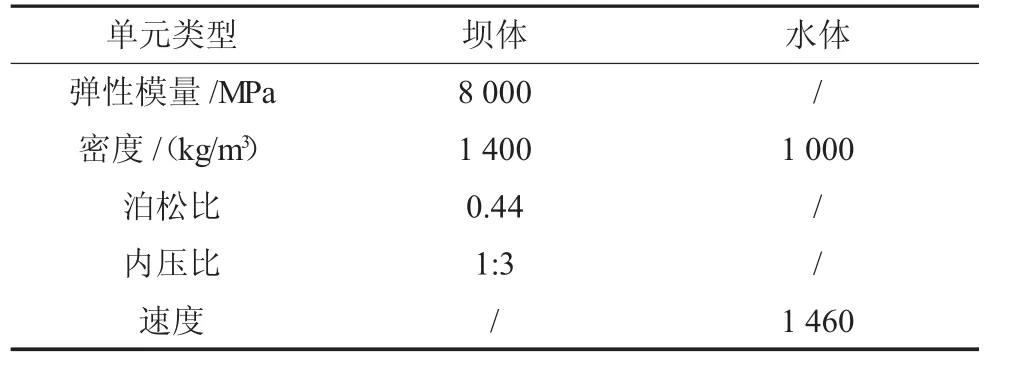
表1 材料參數
橡膠壩袋的固定采用底板施加全約束堵頭式錨固,根據上述相關參數,建立流固耦合條件下橡膠壩壩體模型,共劃分為48956個單元。
2 計算結果分析
為充分預測在不同外界條件下橡膠壩壩體的運營狀態,本次研究共對橡膠壩在不同內壓比、不同高度下前10階振型的自振頻率及周期進行分析研究。高階振型條件下振動圖像及振動方向變得更加復雜,因此文中向平行水流方向,最大振動位移為1.08×10-4m;第2階振型的主振方向為豎直向,最大振動位移為1.04×10-4m;第3階振型的主振方向為平行水流方向,最大振動位移為6.38×10-5m;第4階振型既有順河向又有豎直向,最大振動位移為6.14×10-5m。由此可見,隨著振動階數的上升,橡膠壩壩體的最大位移不斷減小,但在復合振動作用下發生大位移的點不斷增多,破壞更加劇烈。
進一步探討壩高對自振周期和基頻的影響,設定內壓比恒定為1∶3,分別設置壩高為2m、3m、4m、5m,并對4種不同壩高條件下的橡膠壩壩體自振頻率及圓頻率進行分析,可知,在流固耦合條件下,橡膠壩壩體自振頻率、圓頻率隨著壩高的提升而下降,二者與壩高之間近似成指反比例關系,相關性系數分別達到R2=0.9947與R2=0.9943。分析認為,這是由于當橡膠壩壩高持續增長時,壩體的質量也隨之不斷增加,質量的增加使得壩體更加趨于穩定狀態,因此自振頻率與圓頻率不斷降低。
分析不同內壓比條件下,橡膠壩體自振頻率、圓頻率隨內壓比變化的規律。預設內壓比為1∶2.5、1∶3.0、1∶3.5、1∶4.0,分別計算 4 種內壓比下橡膠壩的自振頻率與圓頻率,由壩體自振頻率、圓頻率與內壓比關系曲線可知,流固耦合條件下橡膠壩壩體自振頻率、圓頻率也隨著內壓比的增大而不斷下降,與壩高關系不同的是,自振頻率、圓頻率與內壓比關系成線性關系而非反比例關系,相關性系數分別達到R2=0.9753與R2=0.9800,由此可見具有高度的相關性,充水式橡膠壩壩體在內壓比增大時質量也會隨之增大。
3 防治措施
1)在橡膠壩工程勘察設計選址階段,為增強壩體的穩定性,應將壩址選擇在直段兩岸穩定的河段上;2)抬高壩袋基礎底板,合理控制上、下游水面高度差;3)按照安全性、經濟性原則設計合理的壩高,降低壩體自振頻率;或在某確定壩高條件下,適當提高壩袋內壓,使壩體“剛性”增強,從而減小了脈動荷載幅度,使壩袋不容易發生振動;4)在壩體上每3~5m距離預安裝擾流器或差動式挑坎,破壞溢流水舌真空,避免壩體與水流發生共振現象。

