圓柱殼結構受迫振動特性分析

龐福振, 彭德煒, 李海超, 田宏業, 單衍賀

(哈爾濱工程大學 船舶工程學院，哈爾濱 150001)

柱殼結構廣泛應用于航空航天、船舶、土建、機械等工程領域，在其實際工程應用中將不可避免受外界激擾力作用，因此開展柱殼結構強迫振動特性研究具有重要意義。在此方面，Rayleigh[1]對光圓柱殼的拉伸振動和彎曲振動進行了研究，給出了無限長假設圓柱殼在真空環境中的自由振動固有頻率計算公式。Christoforou等[2]利用解析法分析了兩端簡支圓柱殼在徑向沖擊載荷的振動響應問題。Huang等[3]給出了基于Kirchhoff-Love 假設的有限長兩端簡支圓柱殼體受橫向沖擊瞬態響應的一個封閉解析解。Leissa[4]采用殼體理論對圓柱殼進行了系統深入分析，為解析法求解圓柱殼振動問題奠定了基礎。Qu等[5]提出一種新的方法，即基于區域分解的方法，研究了力激勵下變截面圓柱殼自由振動及力激勵下響應特性。Pang等[6-7]依據Flügge薄殼理論建立振動分析模型，采用Jacobi-Ritz法分析了均厚度以及變厚度圓柱殼、球殼等組合殼體結構的自由及受迫振動特性。

在現有柱殼結構振動分析中，大多是在經典邊界條件下開展的。Yu[8]討論了簡支和固支邊界條件下有限長圓柱殼的振動特性。駱東平[9]采用迭代法求解Flügge方程，以兩端固定、兩端簡支、一端固定另一端自由和兩端自由四種常見的邊界條件為基礎，考察了邊界條件變化對振動頻率的影響，并通過放松或增加某一方向上的約束，討論了不同方向約束的單獨影響。Caresta等[10]研究了低頻下兩端簡支圓柱殼的自由振動并重點討論了呼吸模態即n=0的特性，文中列出了固有頻率下圓柱殼的振型，并討論了三個級別波不同特性及其截止頻率。王宇等[11]基于Love殼體理論對固支-自由約束條件下受徑向載荷的薄壁圓柱殼構件開展受迫振動響應特征分析。汪志強等[12]采用Flügge經典薄殼理論和波傳播方法討論了正交各向異性圓柱殼的自由振動問題，且所提出方法可考慮正交各向異性圓柱殼在復雜和受外力的情況。郭文杰等[13]采用鏡像原理和Graf加法定理得到流體速度勢解析表達式，結合能量泛函變分方法推導出計及自由液面影響的殼-液耦合振動方程，求得圓柱殼固有頻率，為圓柱殼結構流固耦合振動分析提供了新思路。龐福振等[14]基于Flügge殼體振動理論，將改進精細傳遞矩陣法應用于水下加筋柱殼聲輻射問題，分析了經典邊界條件、結構損耗因子、流體介質以及殼體厚度對結構聲輻射的影響。然而，在實際工程應用中，柱殼結構的邊界條件往往存在彈性邊界支撐等復雜邊界條件。因此，本文基于區域能量分解法，開展圓柱殼結構受迫振動特性分析，旨在提出統一的求解公式，為復雜邊界條件下圓柱殼結構受迫振動特性分析提供數據積累和方法依據。

1 柱殼結構區域能量分析模型

圓柱殼結構如圖1所示，結構長為L，半徑為R，厚度為h，結構的坐標系統如圖1所示。

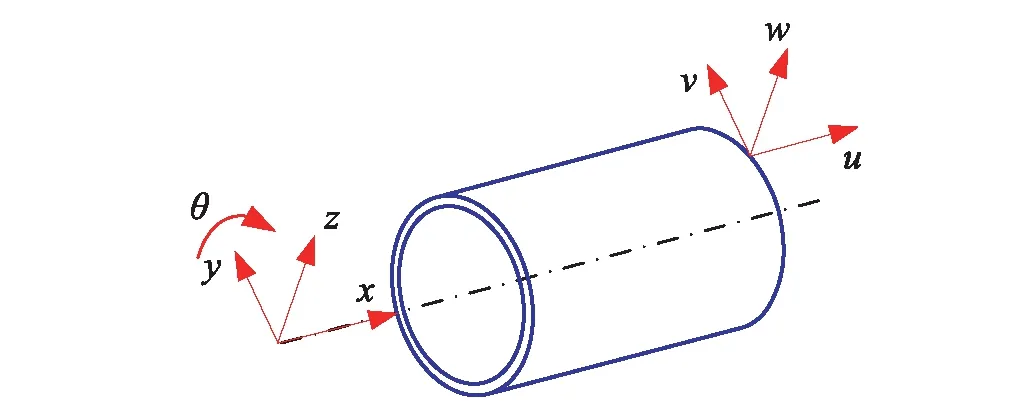
圖1 柱殼結構理論模型Fig.1 Theoretical model of cylindrical shell structure

1.1 柱殼結構的能量泛函建立

將圓柱殼體沿軸線方向均勻地截斷成NL段，即每一段的長度Li=L/NL。根據修正的Hamilton原理，考慮到每一段的能量和相鄰兩段之間的影響，圓柱殼體的總勢能為

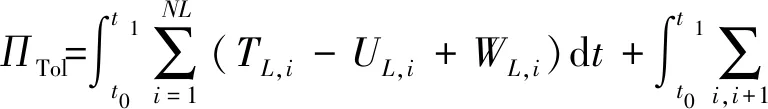
(1)

式中：Tl,i，Ul,i,Wl,i分別為圓柱殼體的第i段的動能、應變能、外力功和附加能量泛函。相鄰分段i～i+1的附加界面勢能表示為K,L。

當忽略圓柱殼體旋轉慣性的條件下，圓柱殼體第i段的動能可以表示為

(2)

式中：ui,vi，wi分別為不同方向位移矢量；ρ為結構質量密度；hi為第i段結構厚度；Si為結構中面面積。

根據Reissner-Naghdi’s線性薄殼理論，i分段的最大結構應變能可以表示為

(3)

考慮到z的奇數次冪和其他相乘在對稱區間的積分為0，可以得到

(4)

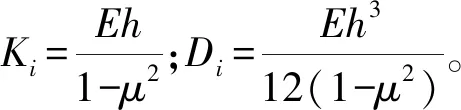
假設外部載荷全部作用在中面位置處，圓柱殼結構的第i分段分布著沿x方向、θ方向、z方向外力fu,i,fv,i,fw,i，此時結構第i分段的外力作功為

(5)

圓柱殼體的第i段、第i+1段的界面上的附加能量泛函為

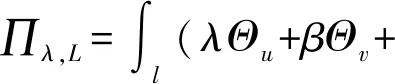
(6)

式中：λ,β,?,ψ分別為柱殼結構分段i與i+1交界面處的未知拉格朗日乘子；Θu,Θv,Θw和Θr分別為柱殼結構分段i與i+1交界面處位移協調方程，可以表示為

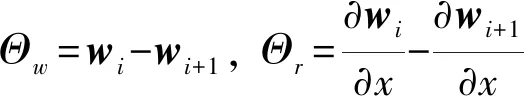
(7)

將式(2)～式(6)代入式(1)，并根據廣義變分原理，對ui，vi，wi，ui，vi+1，wi+1，?wi/?x，?wi+1/?x，λ，β，?和ψ做變分運算，可得到

(8)

(9)

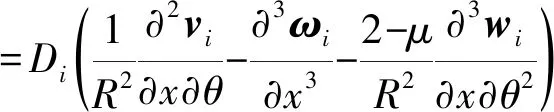
(10)

(11)

將式(8)～式(11)代入式(1)后得到新的能量泛函

(12)

式中：Nx=λ;Nθ=β;Qx=?；-Mx=ψ。

為了保證數值算法的計算穩定性，在式(12)的基礎上添加一項子結構交界面位移連續方程的最小二乘加權參數殘值∏κ,L，此時，結構的完整能量泛函表示為

(13)

(14)

式中：κu,κv,κw和κr為柱殼分段后第i段和第i+1段分區界面加權參數。

在式(14)中引入邊界條件控制參數?u，?v,?w，?r通過控制參數的選取來控制邊界條件。此時的能量泛函可以表示為

(15)

表1給出了多種邊界條件下的控制權參數，可通過選擇不同權參數模擬不同的邊界條件。

表1 不同邊界條件對應的控制參數?t(t=u,v,w,r)

1.2 位移函數的表達式

對于柱殼結構，其位移函數[15]采用Chebyshev行列式[16-17]和傅里葉級數進行展開，系統的位移可以寫成

(16)

(17)

(18)

式中：P和N分別為圓柱殼母線方向上位移分量的Chebyshev多項式截斷值，N為殼體周向位移分量的傅里葉級數截取階數；Φp(x)為Chebyshev行列式，表示圓柱殼體軸向階數；fni(θ)為傅里葉級數，表示圓柱殼體周向波數，它們分別表示為

Φ0(x)=1,Φ1(x)=x,
Φi+2(x)=2xΦi+1(x)-Φi(x)

(19)

fn1(θ)=cos(nθ)+sin(nθ)

(20)

fn2(θ)=sin(nθ)+cos(nθ)

(21)

fn3(θ)=cos(nθ)+sin(nθ)

(22)

2 柱殼結構振動求解

2.1 柱殼結構受迫振動特性方程的求解

在上文中建立了柱殼結構的廣義能量泛函，但是并未推導出結構的受迫振動特性求解方程。柱殼結構的整體能量泛函可以表示為

(23)

由前面級數的位移表達式可知，柱殼結構分段i的位移容許函數ui，vi，wi由三角級數與第一類正交切比雪夫多項式表示，從式(15)～式(18)可以看出，位移表達式中都存在關于時間的未知位移系數式。因此，式(23)對未知位移系數進行變分運算，可得到結構的受迫振動特性方程

(24)

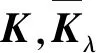
(25)

其中，

(26)

(27)

(28)

在本文中，不直接對式(24)進行求解，而是提出另外一種求解過程，將求解問題轉化到廣義系統坐標中，減少了廣義坐標以后的運動方程表示為

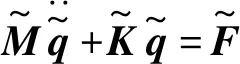
(29)

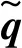
(30)

(31)

將其代入式(15)～ 式(17)即可得到在不同頻率下結構的穩態響應。

2.2 收斂性分析

在結構的受迫振動特性分析展開之前，需要對最小二乘加權參數的收斂性進行分析，得出最佳的最小二乘加權參數。根據前面所定義的邊界條件，選取F-E邊界條件，即柱殼結構的左端為自由邊界，結構的右端為彈性邊界，彈性參數取值為ku=kv=2×108N/m，結構參數為：L=6 m，R=1 m，h/R=0.01，E=210 GPa，ρ=7 800 kg/m3，μ=0.3。位移容許函數在母線方向上的切比雪夫正交多項式的截斷值為8，結構分段數NL=2。頻率無量綱化計算公式為

Ω=ωR(ρ(1-μ2)/E)1/2

(32)

表2給出了不同周向波數下，不同最小加權參數對結構前五階無量綱化固有頻率的影響，可以看出，當加權參數增大時，結構的固有頻率也隨之增大，當加權參數達到某一個臨界取值時，結構的計算結果趨于穩定。在實際數值計算中，加權參數的取值不可能無窮大，同時為保證計算的絕對數值穩定性，根據表2中計算結果，在后續的計算中，最小二乘殘差加權系數取值為κ=1×1014。

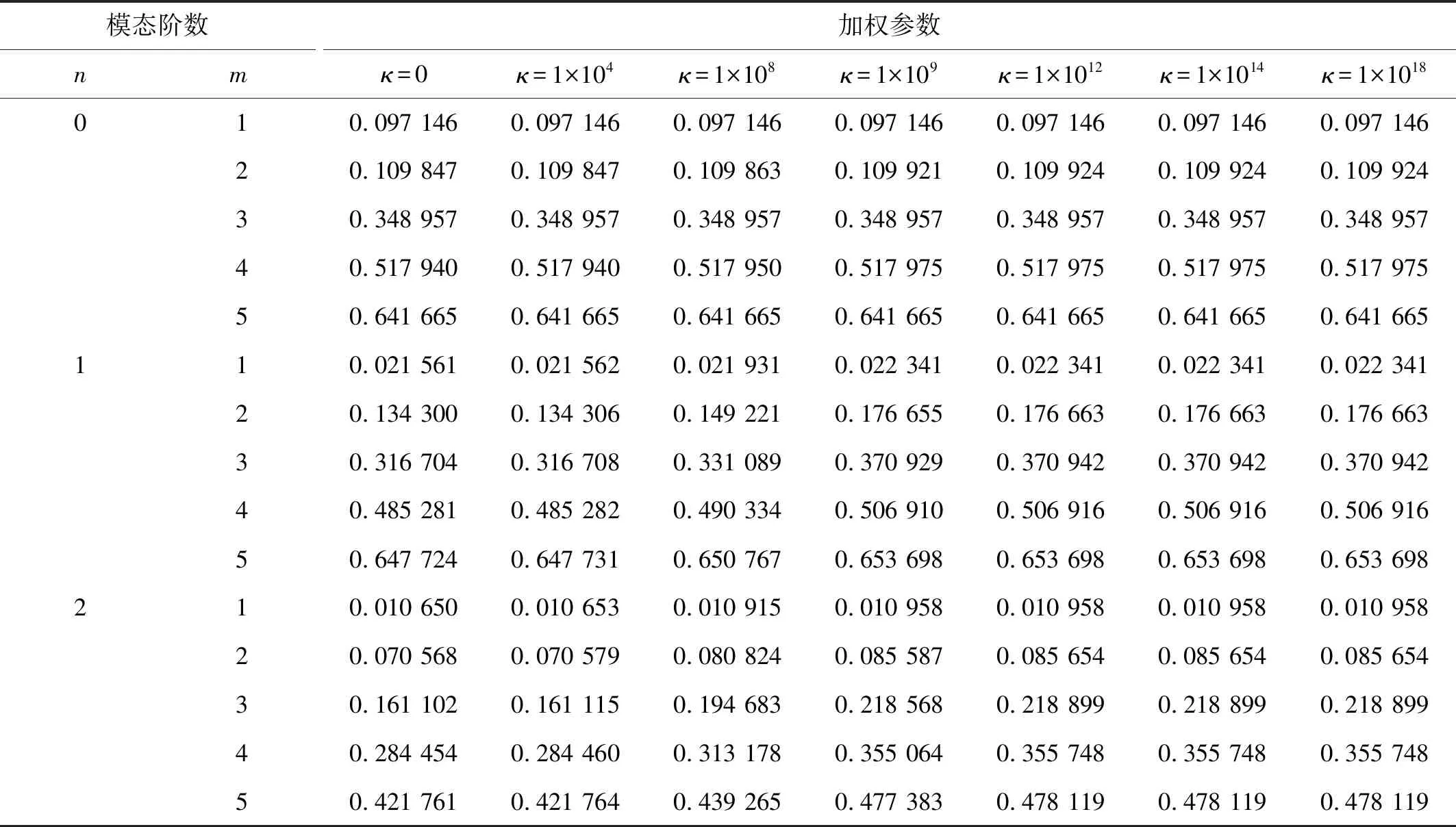
表2 最小二乘加權參數收斂性分析

在對加權參數分析的基礎上，由本文的計算模型可知，對結構進行分段時，殼段數不可能無限大，只有選取合理的分段數，才能保證數值計算的計算效率和精度，因此需對分段數的收斂性進行分析。結構參數與表2所用計算模型保持一致，并且加權參數取值為κ=1×1014。表3給出了不同分段數下對結構不同階數的無量綱化固有頻率Ω的影響，無量綱化公式與表2保持一致，為了驗證收斂性分析的正確性，有限元計算所得的結果作為參照值也在表3中列出。

由表3可以看出，當NL=8時，其計算結果與已經保持在小數點后六位保持一致，因此，在后續的計算中，如不做特別說明，柱殼分段數取值為NL=8。

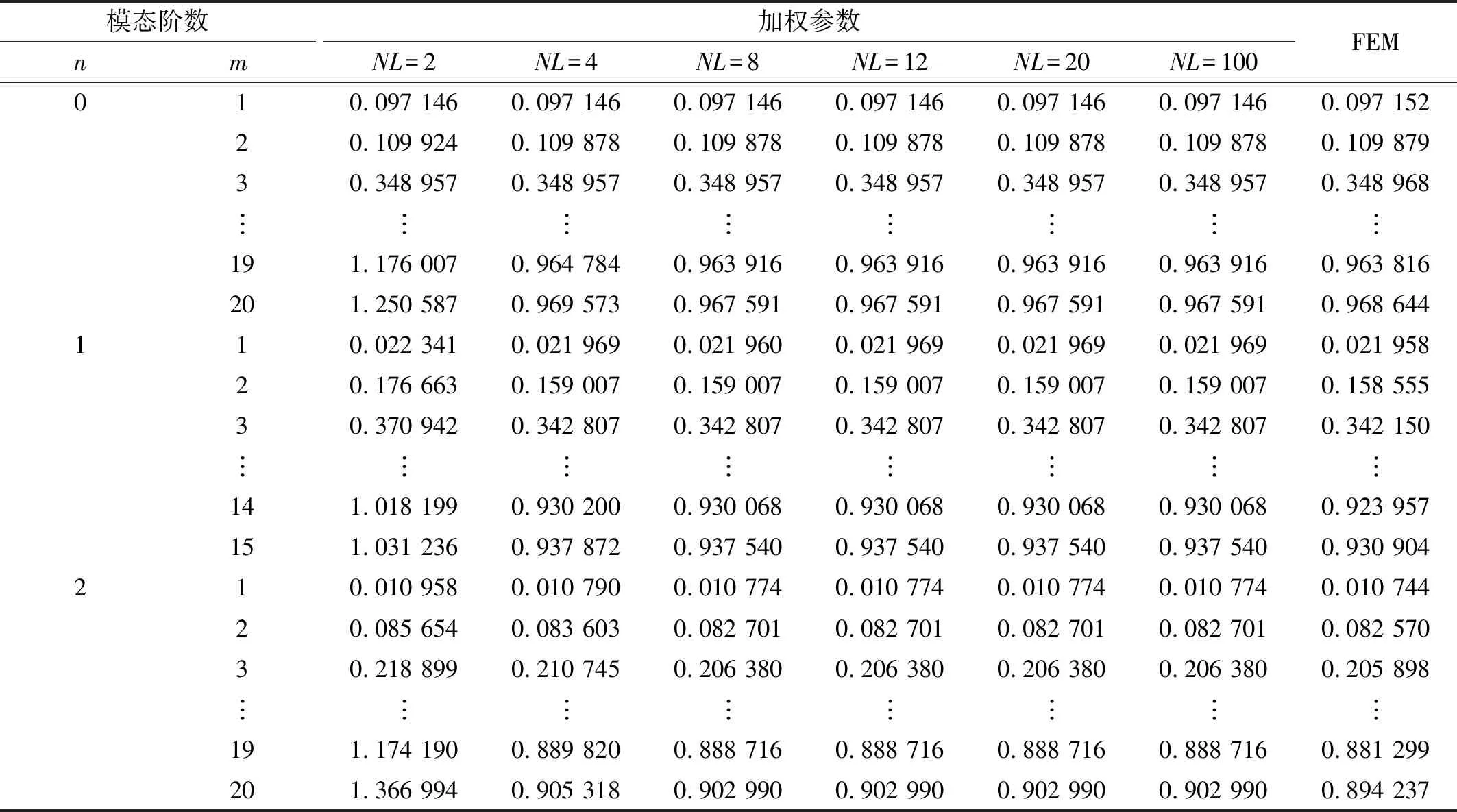
表3 區域分段數的收斂性分析

3 柱殼結構受迫振動響應研究

3.1 模型驗證

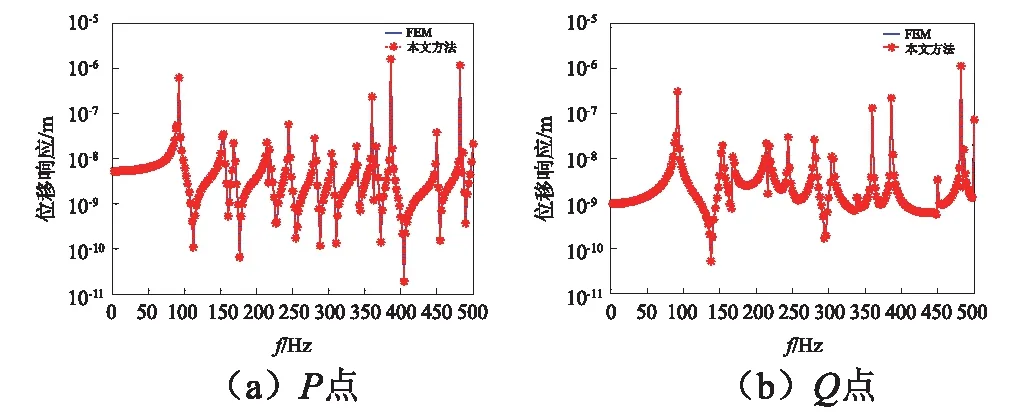
圖2 C-C邊界條件下受徑向載荷圓柱殼位移響應曲線Fig.2 Displacement response of cylindrical shell with radial load under C-C boundary condition

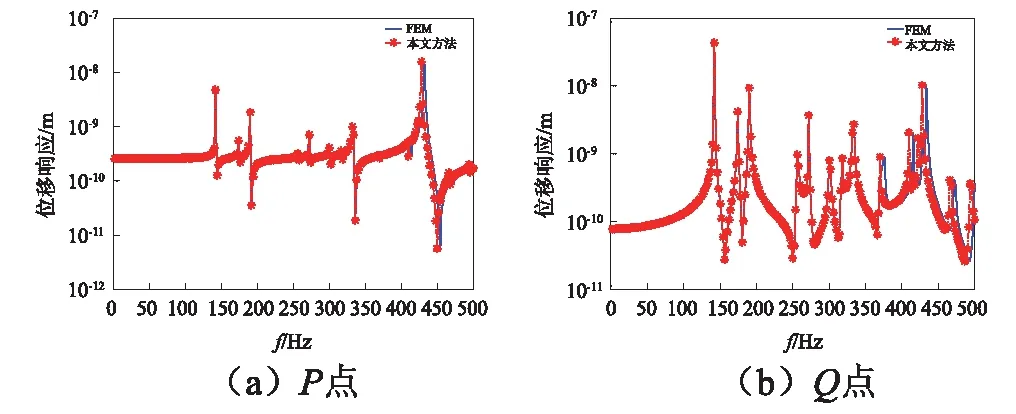
圖3 C-C邊界條件下受軸向載荷圓柱殼位移響應曲線Fig.3 Displacement response of cylindrical shell with axial load under C-C boundary conditions

通過圖2與圖3的對比可以發現，當圓柱殼受徑向載荷時，在0～500 Hz內，本文所用方法計算得到的振動響應值與有限元方法計算得到的振動響應值擬合良好；當圓柱殼受軸向載荷作用時，在0～350 Hz內，本文方法計算得到的振動響應值與有限元方法計算得到的振動響應值擬合良好，在350～500 Hz內，兩種方法計算得到的振動響應值在量級上保持一致，峰值產生一定偏移，最大偏移誤差為0.56%，因此可證明本文方法的正確性。從圖中還可以看出，在低頻段波峰較小，在高頻位置處波峰較為密集，并且在眾多波峰值中，在結構的第一階固有頻率處其響應峰值最大，這也是在實際工程中總是關注結構基頻的原因。

3.2 邊界條件對柱殼結構受迫振動響應的影響

給出不同彈性邊界條件下在相同的單位激勵下P點與Q點的位移響應曲線，定義彈性邊界E1(u=v=w=0,?w/?v≠0)。

由圖4可知，當圓柱殼的邊界條件發生改變時，相同激勵載荷作用下其位移響應曲線會發生相應變化，共振波峰的數目以及共振幅值都會發生變化。在相同的掃頻范圍內，SS-SD邊界下的波峰數目最多，其次為C-F，最小為C-C；當約束剛度變大時，結構固有頻率的波峰會發生右移，但結構的一階固有頻率幾乎不發生變化。

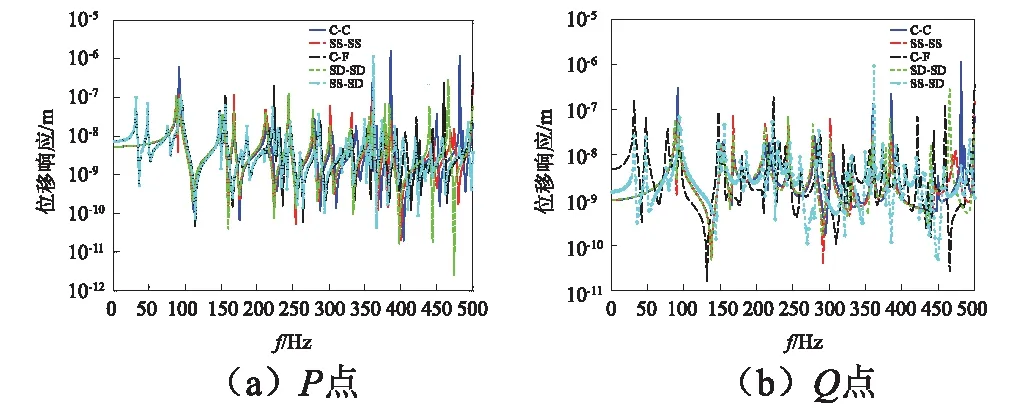
圖4 不同邊界條件下受徑向載荷作用的圓柱殼位移響應曲線Fig.4 Displacement response of cylindrical shell with radial load under different boundary

圖5 不同彈性邊界下受徑向載荷作用的圓柱殼位移響應曲線Fig.5 Displacement response curve of cylindrical shell with radial load under different elastic boundary

從圖5可以看出，當彈性邊界彈簧剛度值逐漸增大時，結構響應曲線的總體趨勢向著高頻方向發生小范圍的移動，共振波峰處頻率值逐漸增大，位移響應的整體幅值也隨著波峰移動發生變化。此外，當K的剛度值從1×104增加至1×106時，結構的共振峰值幾乎不發生變化，說明此剛度范圍對結構的受迫振動影響較小，隨剛度值進一步增加，曲線發生了明顯的移動，表明圓柱殼結構對1×106以后的剛度值變化較為敏感。

3.3 結構參數對柱殼結構受迫振動響應的影響

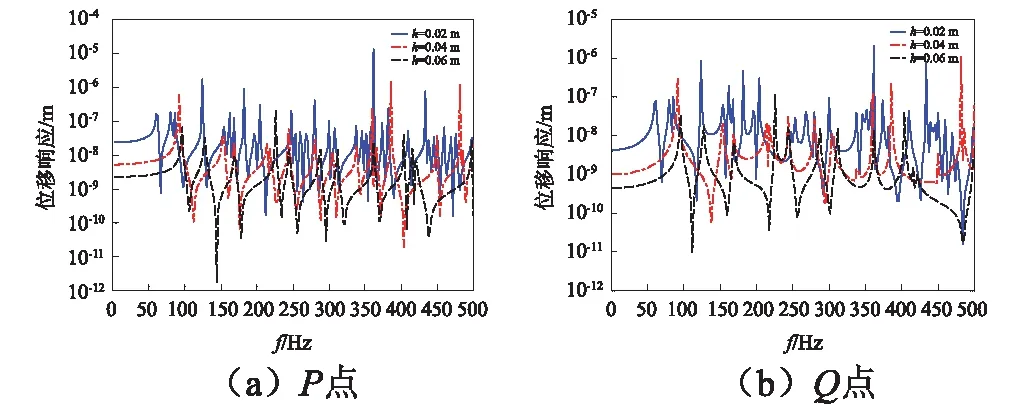
圖6 在C-C邊界條件下受徑向載荷時不同厚度圓柱殼的位移響應曲線Fig.6 Displacement response curves of cylindrical shells with different thickness under radial load under C-C boundary conditions

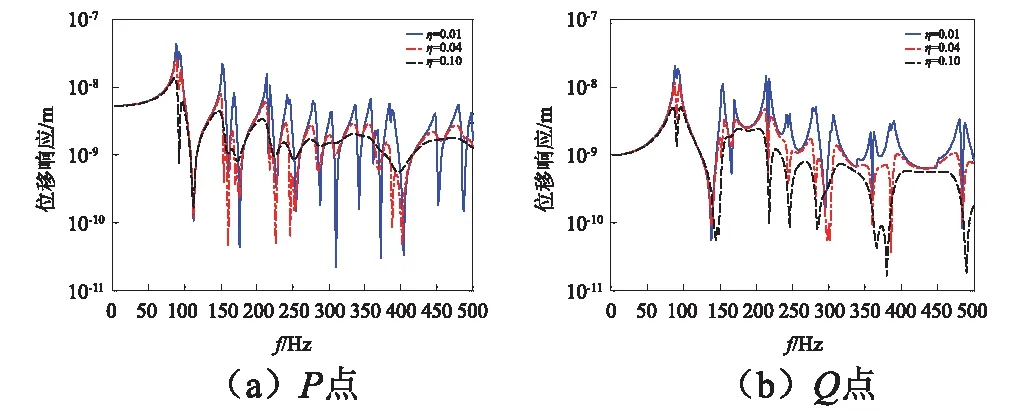
圖8 在C-C邊界條件下受徑向載荷時不同阻尼系數圓柱殼位移響應曲線Fig.8 Displacement response curves of cylindrical shells with different damping coefficients under the radial load under the C-C boundary condition

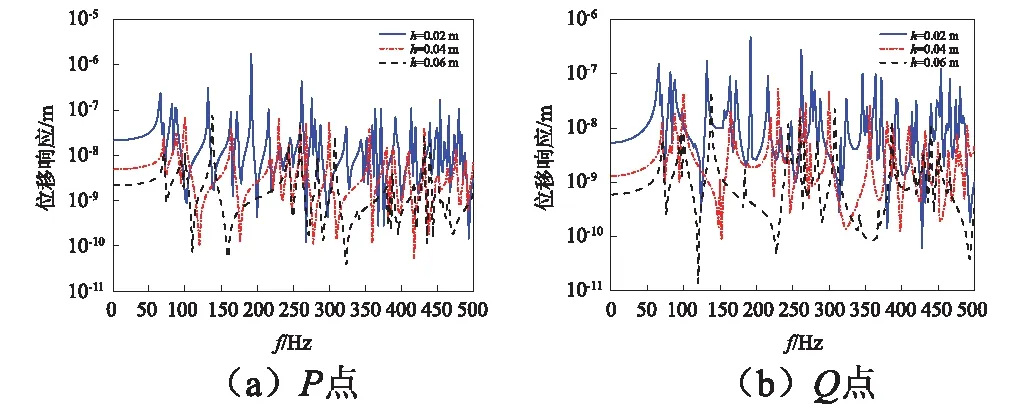
圖7 在E2-E3邊界條件下受徑向載荷時不同厚度圓柱殼的位移響應曲線Fig.7 Displacement response curves of cylindrical shells with different thickness under radial load under E2-E3 boundary conditions

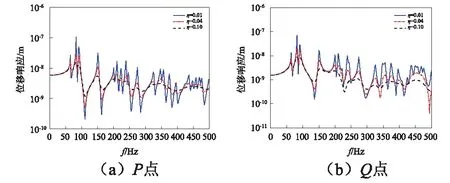
圖9 在E2-E3邊界條件下受徑向載荷時不同阻尼系數圓柱殼位移響應曲線Fig.9 Displacement response curves of cylindrical shells with different damping coefficients under the radial load under the E2-E3 boundary condition

從圖6與圖7可以看出，殼結構厚度發生變化時，結構的響應曲線發生了較大的變化，在相同的頻率范圍內，結構的厚度越小，其波峰的數量越多，且響應值越大，由此可知，結構殼體的厚度可使結構振動特性發生較大改變。從圖8與圖9可以看出，結構損耗因子增大時，結構的共振峰頻率幾乎不發生改變，而共振峰處的響應幅值明顯降低很多，這是由于損耗因子的增大，使得結構自身對外界能量吸收更多，導致其響應值下降，由此可知，損耗因子的改變，不影響結構的固有頻率，僅對其響應產生一定的影響。

4 結 論

本文基于區域能量分解法，建立了結構受迫振動計算分析模型，研究了邊界條件和結構參數的變化對結構動態響應的影響，并通過與有限元方法的計算結果進行對比，驗證了本文方法的正確性，通過本文研究，可得如下主要結論：

(1) 通過與有限元的仿真計算結果對比發現，本文方法的柱殼分段數在NL=8時區域收斂，最小二乘殘差加權系數取值達到κ=1×1014時結構的數值計算具有良好的穩定性。

(2) 除第一階固有頻率外，經典邊界約束剛度的不同對于結構的固有振動特性的影響較大；而在彈性邊界條件下，邊界彈簧剛度值的選取對結構的固有振動特性有較大的影響，且存在一個較為敏感的區域，使得結構的固有振動特性發生較大的變化。

(3) 相同頻率范圍內，結構厚度越小，共振峰值就越多，響應值也越大；而對于結構損耗因子來說，其只影響結構的共振峰值，對于共振頻率點的位置影響較小。