基于模型曲率變化的3D打印分層厚度優化研究
蔡盼盼 魯忠臣 郭浩亮

摘要:根據3D打印工藝特點,產品的成型質量和成型時間與分層厚度密切相關。現有的等厚度分層算法方法簡單、分層速度快,但成型質量普遍不理想,因此提出一種基于模型曲率變化優化設置分層厚度的自適應算法,建立成型質量、成型時間與分層厚度的多目標優化模型。采用Python語句編寫程序并進行實例驗證,結果表明,提出的自適應分層算法相較于等厚度分層算法可有效改善成型質量和縮短成型時間。
關鍵詞:3D打印;分層厚度;自適應分層算法;多目標優化
中圖分類號:U615
文獻標識碼:A
DOI: 10.15913/j.cnki.kjycx.2019.08.011
隨著3D打印技術的不斷普及和應用,產品的成型質量和成型時間越來越受到重視。研究表明,成型質量與成型時間均與分層厚度密切相關——分層厚度設置越小,成型質量越好而成型時間越長;反之,分層厚度越大,成型時間越短,成型質量越差,因此如何優化設置分層厚度至關重要[1]。目前,3D打印普遍采用等厚度分層算法,即各層分層厚度保持一致,該類分層方法雖實現簡單,分層速度快,成本較低,但成型質量普遍不理想。因此,本文提出一種根據模型的曲率變化優化設置分層厚度的自適應算法,即首先通過分析成型質量和分層厚度的函數關系、成型效率和分層厚度的函數關系,建立多目標優化模型。
1 多目標優化模型的建立
成型質量和成型時間是衡量3D打印的重要因素。本文通過分析STL模型的分層特點和成型工藝特點[2],分別建立成型質量、成型時間與零件成型方向、分層厚度之間的函數關系[3]。
1.1 以成型質量為目標的函數建立
3D打印的成型質量主要指成型表面的粗糙度和加工精度。通過計算原型軸向截面面積與打印產品軸向截面積的誤差△S來衡量成型質量。截面積誤差如圖1所示。
根據圖幾何關系,推導得出單位分層厚度上的截面面積誤差△S,即:
1.2 以成型時間為目標的函數建立
D打印的時間主要由粉末鋪平時間、噴墨粘結時間、工作臺下降時間以及其他輔助時間構成。其中噴墨粘結時間由成型方向和分層厚度決定,粉末鋪平時間和工作臺下降時間由分層層數決定,而分層層數取決于分層厚度,因此可通過增加分層厚度的方式來提高成型效率。因此,本文以成型時間為目標的優化模型可建立為T=1/h.
1.3 多目標優化模型的建立
綜上所述,本文以分層厚度h為設計變量,成型質量與成型效率為目標建立多目標優化數學模型,求解在某一高度上的分層厚度的解,建立的數學模型如下:
由于分層厚度與打印質量并不完全成正比。分層厚度過大將導致激光束不能穿過燒透該燒結層(對SLA和SLS等方法而言),層與層之間連接不牢靠,造成分層;而過小的分層厚度又會導致已燒結部分重新燒結,降低成型精度。因此,本文將分層厚度h的取值范圍設置為h∈[0.1,0.31,單位為mm。
2 多目標優化模型的求解
在3D打印技術中,成型質量與成型時間相互制約,在優化其中一項的過程中必然會削弱另外一項,優化后得到一組內部不存在相互支配關系的非支配最優解集。因此,本文采用簡單的交互規劃法,引入Rate變量構造新的目標函數:式(3)中:Rate變量為成型時間優化需求與打印質量優化需求的比值,范圍為[0.005,0.02]。
本文采用Python語言編制計算程序并求解。
3 實例驗證分析
3.1 驗證樣本
為了進一步驗證優化算法的有效性與可行性,選用細頸瓶進行實例驗證,細頸瓶節點坐標如表1所示。
3.2 優化算法的驗證及分析
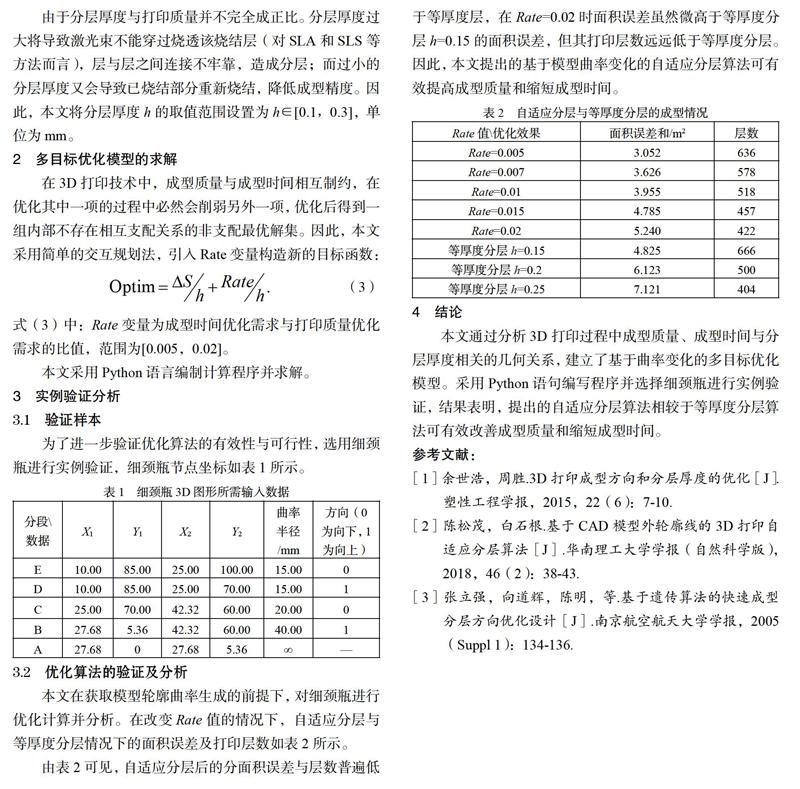
本文在獲取模型輪廓曲率生成的前提下,對細頸瓶進行優化計算并分析。在改變Rate值的情況下,自適應分層與等厚度分層情況下的面積誤差及打印層數如表2所示。
由表2可見,自適應分層后的分面積誤差與層數普遍低于等厚度層,在Rate-0.02時面積誤差雖然微高于等厚度分層h-0.15的面積誤差,但其打印層數遠遠低于等厚度分層。因此,本文提出的基于模型曲率變化的自適應分層算法可有效提高成型質量和縮短成型時間。
4 結論
本文通過分析3D打印過程中成型質量、成型時間與分層厚度相關的幾何關系,建立了基于曲率變化的多目標優化模型。采用Python語句編寫程序并選擇細頸瓶進行實例驗證,結果表明,提出的自適應分層算法相較于等厚度分層算法可有效改善成型質量和縮短成型時間。
參考文獻:
[1]余世浩,周勝.3D打印成型方向和分層厚度的優化[J].塑性工程學報,2015,22 (6): 7-10.
[2]陳松茂,白石根.基于CAD模型外輪廓線的3D打印自適應分層算法[J].華南理工大學學報(自然科學版),2018, 46 (2): 38-43.
[3]張立強,向道輝,陳明,等.基于遺傳算法的快速成型分層方向優化設計[J].南京航空航天大學學報,2005(Suppl l):134-136.

