基于Wiener過程和Kalman修正的速率陀螺儀剩余壽命預測

賀志遠，呂衛民，胡文林

(海軍航空大學， 山東 煙臺 264001)

速率陀螺儀是導彈姿態控制系統的重要組成部分，它控制著飛行過程角速度的輸出，一旦出現故障將影響飛行精度，導致飛行失控甚至彈體自毀。速率陀螺儀作為一種高精密的設備，內部包括眾多電子元器件、傳感器以及機械連接部分。它的性能隨著工作時間逐漸改變，同時，受到環境因素(溫度、濕度、振動)的影響，可能出現電路短路、斷路、傳感器失靈以及機械部件變形等失效。因此，對速率陀螺儀進行可靠性評估，合理預測剩余壽命，對于保證導彈的安全性具有重大意義。

傳統的可靠性評估方法主要是根據失效機理建立模型進行失效分析，但是隨著設備復雜程度的提高，很難建立起可靠的的失效物理模型[1]。針對這一問題，基于性能退化數據的分析方法出現，該方法利用設備性能隨時間變化過程中的數據，建立性能退化模型，計算過程較為簡便且結果具有較高的可靠度，已成為可靠性評估及壽命預測的重要手段之一[2-4]。目前，性能退化模型主要包括隨機系數模型和隨機過程模型。Lu等[5]最早使用隨機系數模型研究退化過程，文獻中假定模型的參數服從某種隨機分布。這種方法的弊端在于，研究對象的參數一旦確定，其退化軌跡就確定，體現不出退化過程的隨機性。而基于隨機過程模型的方法解決了這一問題，該模型很好的體現了退化過程的不確定性，更加符合設備的實際退化規律。隨機過程模型中主要包括Gamma過程和Wiener過程等， Yuan[6]建立Gamma過程退化模型對核電站某些元件的性能進行可靠性評估。王浩偉等[7]提出利用Gamma過程參數的非共扼先驗分布進行Bayesian統計推斷的剩余壽命預測方法。Gamma過程的退化增量是非負的，且嚴格單調遞增，適用于單調變化的退化過程。而Wiener過程具有不嚴格單調的特性，計算分析特性較好，適用于退化過程具有波動性的產品。Park等[8]利用Wiener過程建立模型，對在加速應力條件下得到的退化數據進行處理。王小林[9]通過Wiener過程隨機模型預測了金屬化膜電容器的剩余壽命。

速率陀螺儀退化過程具有波動性，并非單調過程，本文采用Wiener過程建立隨機模型進行計算。但是由于現實工作環境及設備本身的復雜性，退化建模過程還存在以下問題：① 設備內部組件較多，包含了電子部分和機械部分，退化規律不同，導致設備整體退化軌跡呈現非線性。線性Wiener過程已經無法有效的研究設備的退化過程，有些學者提出將非線性過程通過某種尺度轉化為線性過程的方法[10]，王浩偉等[11]通過時間尺度轉化方法將指數退化模型轉化為線性模型對電連接器的可靠性進行了研究。雖然這種方法簡化了計算過程，但結果的精確性也相應降低，而且有些退化模型無法轉化為線性過程。② 不同于飛機等航空裝備高頻使用的特點，導彈裝備的壽命更長，在全壽命周期內要經歷不同的任務階段，為了方便研究，分為運輸、貯存、戰備三個階段，每個階段的環境因素不完全相同，內部設備退化的主導機理也在改變，退化趨勢呈現階段性。針對多階段退化問題，部分學者提出建立多階段退化模型。袁慶祥等[12]引入轉換函數改進Wiener過程，建立了多階段退化模型預測電機的剩余壽命。該方法有效解決了多階段退化問題，但是引入了新的函數，計算難度增大。

針對速率陀螺儀退化過程的非線性、多階段的特點，本文采用Wiener過程建立非線性退化模型，利用收集到退化數據進行模型參數的估計，然后根據Kalman濾波算法對模型進行參數修正，實現退化過程的多階段性，使剩余壽命預測結果更加精確。

1 剩余壽命預測模型

1.1 非線性退化模型

導彈壽命周期經歷的環境因素復雜，內部設備的真實退化軌跡很難估計，也并非時間的線性函數，根據這一退化特點，本文建立基于Wiener過程的非線性退化模型。假設該設備退化過程只有一個關鍵性能參數，則非線性退化模型表示如下：

(1)

式中：X(t)為時刻t的性能退化量，X(0)為初始時刻的性能退化量(為了體現模型的一般性，令X(0)=0)；μ(t;θ)為非線性函數，顯然，當μ(t;θ)=μ時，上式轉化為一般Wiener過程；σB為擴散系數；B(t)為標準布朗運動。

1.2 壽命分布

當產品的性能退化量達到預設的臨界水平時，就認為此時產品失效，這一臨界水平稱為失效閾值。假設該產品的失效閾值為ω，產品的壽命為T，且產品的性能退化軌跡由非線性Wiener過程描述，則產品的壽命T可定義為產品的性能退化量X(t)首次達到其失效閾值ω的時間，即

T={t∶X(t)≥ω|X(0)<ω}

(2)

假定μ(t;θ)和σB為固定未知參數，μ(t;θ)是關于t的可導函數，根據文獻[13]，壽命T的概率密度函數為：

(3)

其中：

Ε(t;θ)=Λ(t;θ)-tΛ′(t;θ)

給定一個漂移系數λ，令μ(t;θ)=λbtb-1(b為固定參數)，壽命T的概率密度函數可表示為：

(4)

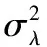
引理如果Z～N(μ,σ2)，A，B，C，ω∈R，那么

(5)

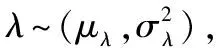
Eλ[fT|λ(t|λ)]

(6)

其中，p(λ)為λ的概率密度函數。

進一步可得，

(7)

可靠度函數可表達為：

(8)

1.3 剩余壽命預測

假設特定產品在tn和tn+l時刻的性能退化量分別為X(tn)和X(tn+l)，按照Wiener過程獨立增量的性質，可得

(9)

令

Z(l)=X(tn+l)-X(tn)=

(10)

顯然式(9)是一個由布朗運動B(l)驅動的新的隨機退化過程。

產品的剩余壽命是指從當前時刻到產品發生失效時刻的時間間隔，根據壽命的定義可知特定個體產品在時刻tn的剩余壽命l可表示為：

L=inf{l∶X(tn+l)≥ω}

(11)

獲得產品剩余壽命的關鍵是找到剩余壽命的概率密度函數。按照Wiener過程獨立增量性質，結合式(9)、式(10)，可得

L=inf{l∶X(tn+l)≥ω}=

inf{l∶X(tn+l)-X(tn)≥ω-X(tn)}=

inf{l∶Z(l)≥ω-X(tn)}

(12)

特定個體產品在時刻tn的剩余壽命l，即隨機過程退化量Z(l)首次達到閾值ω-X(tn)的時間。

結合式(3)、式(11)，可得tn時刻剩余壽命l的概率密度函數：

(13)

根據全概率公式，由式(13)可得，可靠度函數為式(14)：

(14)

2 參數估計

2.1 EM算法

上述非線性退化模型的未知參數設為Θ=(μλ,σλ,b,σB)。其中，b和σB為固定系數，描述各階段退化過程的共性。μλ和σλ為隨機系數，通過修正來描述不同階段退化的過程的特性。

假設可測退化數據的設備有n臺，分別在時刻t1，t2，t3，…，tm對設備進行測試，得到第i臺設備在時刻j的性能退化數據Xi={X(t1,i),X(t2,i),…,X(tj,i)}，相應的退化增量為ΔX(tj,i)，因此

ΔX(tj,i)=X(tj,i)-X(tj-1,i)=

(15)

其中，λi為漂移系數的真實值。

未知參數增加為Θ=(λi,μλ,σλ,b,σB)。

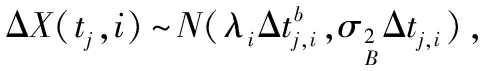
根據式(16)以及最優解搜索算法，可以得到未知參數的極大似然估計值，但計算過程較為復雜且未知參數數量較多，針對這一問題，本文采用Gibbs抽樣算法來估計未知參數。

2.2 Gibbs采樣算法

Gibbs采樣是馬爾科夫蒙特卡洛(Markov Chain Monte Carlo，MCMC)方法的一種，用于在難以直接采樣時從多變量概率分布中抽取樣本，尤其在高維參數的情形下，Gibbs采樣有更大的優勢。Gibbs采樣算法實質上是M-H抽樣時，接受概率等于1的特例，但由于其原理簡單且適用范圍廣泛，因此被認為是一種特殊的抽樣算法。

Gibbs采樣算法的步驟如下：

1) 給定未知參數λi,μλ,σλ,b,σB的聯合分布函數和先驗分布函數，分別為p(λi,μλ,σλ,b,σB)和p(λi),p(μλ),p(σλ),p(b),p(σB)；

3) 計算出未知參數λi的條件概率密度，可表示為

(17)

同式(17)，分別計算其他未知參數的條件概率密度；

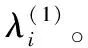
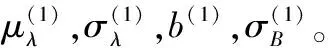
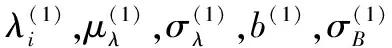
(18)

6) 使用收斂后的函數q(λi,μλ,σλ,b,σB)替代p(λi,μλ,σλ,b,σB)，重復3)、4)過程k次，得到k組Gibbs樣本。

最后，利用k組Gibbs樣本和貝葉斯公式計算未知參數的后驗分布，進一步得到未知參數的估計值。

3 基于Kalman濾波算法的多階段參數修正

Kalman濾波是一種高效的遞歸濾波器，建立在隱馬爾科夫模型的基礎上。它利用目標的動態信息，去掉噪聲干擾，得到關于目標位置的估計。這個估計包括：濾波(對當前位置的估計)、預測(對將來位置的估計)和平滑(對過去位置的估計)[15]。

速率陀螺儀的退化過程具有明顯的多階段性，為了更加準確地預測剩余壽命，通過Kalman濾波算法對各階段模型參數進行修正[16]，根據式(4)可知，修正對象為漂移系數λ。

假設在時刻tn進行漂移系數的修正，根據式(1)并結合Kalman濾波算法原理，選取狀態空間方程如下：

(19)

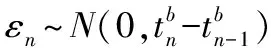
多種色釉于一坯胎中也是在近現代才流行起來，多種色釉的窯變比單色釉可說難，也可說易。難是難在對釉料料性的掌握，那種色釉流動，那種不流動，色釉與色釉之間能否結合，產生的效果如何，幾種色釉結合當怎樣的比例才能燒制出最佳效果等等，這就是難。說它容易，也只能說出現二次創作以后陶瓷藝術家才敢如此認為。顏色釉基礎上的二次創作是根據藝術家對色釉窯變效果來巧妙裝飾的，主觀性較強，但選取的畫面需要和色釉窯變氣氛相吻合，才能達到異曲同工之妙。

誤差項νδ可能是正值也可能是負值，這將影響到λn的正負，根據文獻[17]，本文研究對象的漂移系數非負，為此確定了一個新的狀態空間方程：

(20)

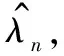
根據Kalman濾波算法及文獻[14]，引入衰減系數γ(ti)。

γ(ti)=max{γ(ti),1}

(21)

且

其中，其中η為遺忘因子，0.95<η<1。

(22)

且

Pi|i-1=γ(ti)Pi-1|i-1

更新方差Pi|i。

(23)

最后，當i=n時，完成時刻tn漂移系數的階段更新，修正后的退化模型可表示為

(24)

4 實例分析

通過對速率陀螺儀進行故障模式、機理及影響分析，發現壽命周期內其性能指標受到溫度、濕度及振動等環境因素的影響。通過查閱相關文獻，本文選取零偏值(°/h)作為性能退化指標。試驗對象為6臺速率陀螺儀，為了模擬該設備的工作特點，驗證多階段非線性模型的準確性，選取不同的溫度應力(0～1 000 h，20 ℃；1 000～2 000 h，55 ℃；2 000～3 192 h，70 ℃)進行退化試驗，試驗過程共進行20次數據采集，每次間隔168 h，測試數據如表1所示。其中前4臺測試數據用于模型參數估計，后2臺測試數據用于多階段參數的修正。試驗的失效閾值設置為0.5(°/h)。

從圖1可以看出不同溫度應力下，零偏測試數據的退化存在著明顯的差異，與上文多階段退化的假設相符。

利用測試數據，通過Gibbs采樣算法計算得到非線性退化模型的未知參數，再將計算結果與極大似然估計方法(EM)結果一起，列于表2。采用Gibbs采樣算法，模型的擬合殘差均方差(MSE)較小，說明該方法估計的參數更加符合實際數據的趨勢。

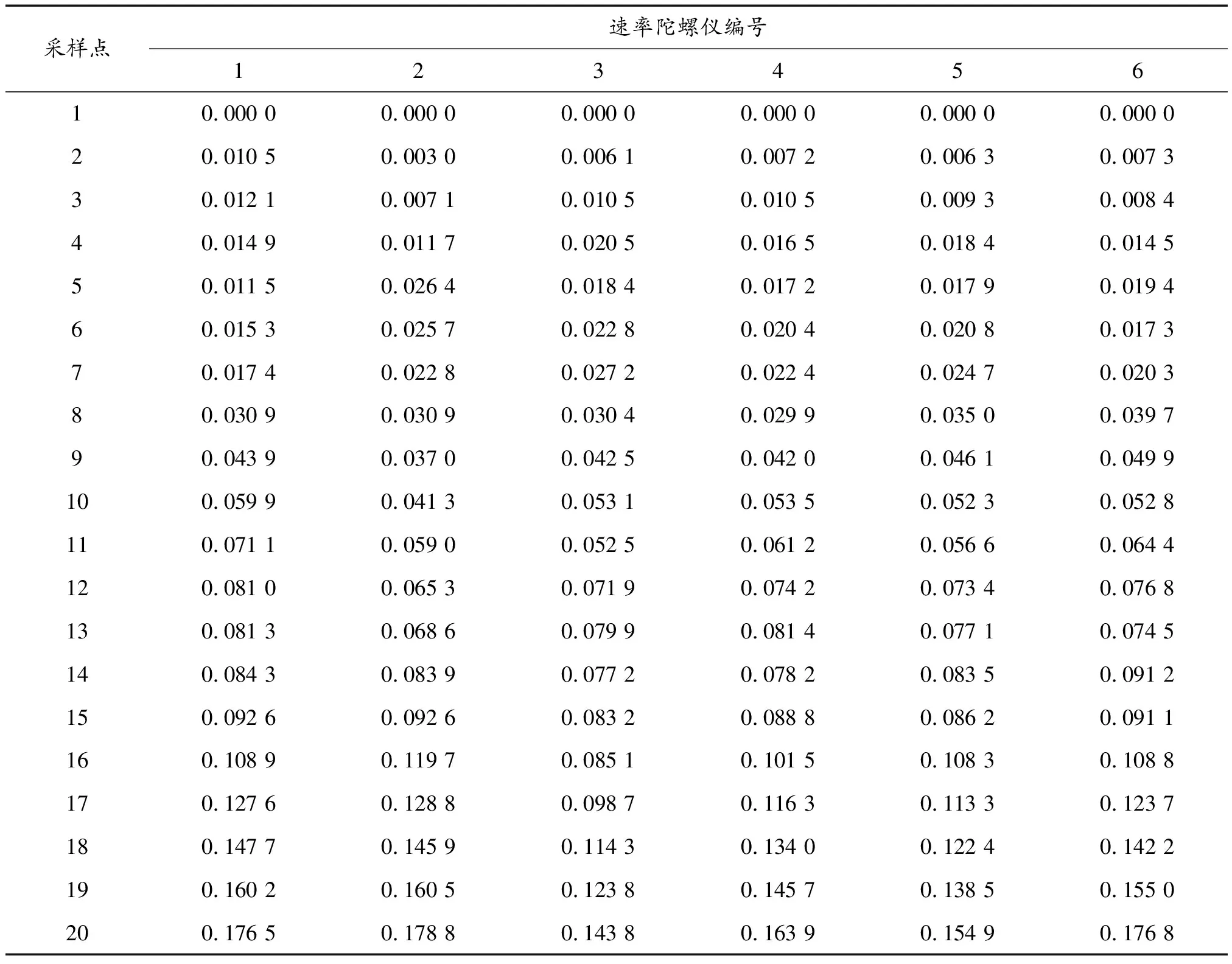
表1 速率陀螺儀零偏測試數據 (°/h)

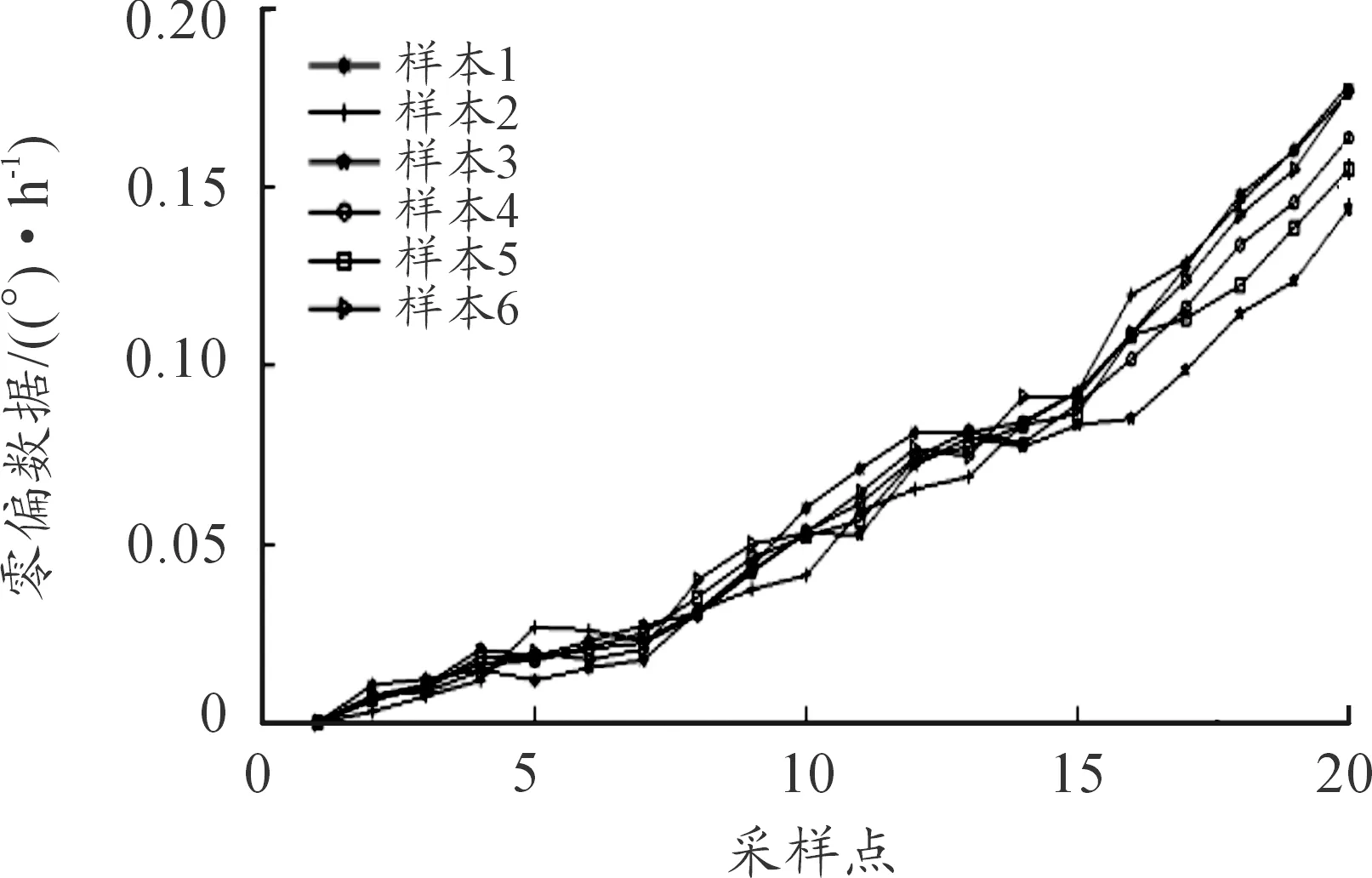
圖1 零偏測試數據

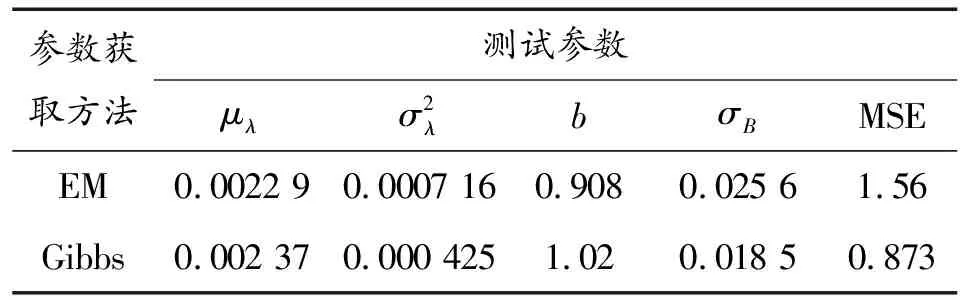
參數獲取方法測試參數μλσ2λbσBMSEEM0.0022 90.0007 160.9080.025 61.56Gibbs0.002 370.000 4251.020.018 50.873

再運用Kalman濾波方法對各階段退化模型的參數進行修正，修正后的參數如表3所示，并通過AIC準則與單階段非線性退化模型參數進行比較，AIC值越小說明參數更加符合模型。

AIC=-2(maxl)+2p

(25)

其中，maxl表示最大似然函數的值；p表示模型未知參數的個數。

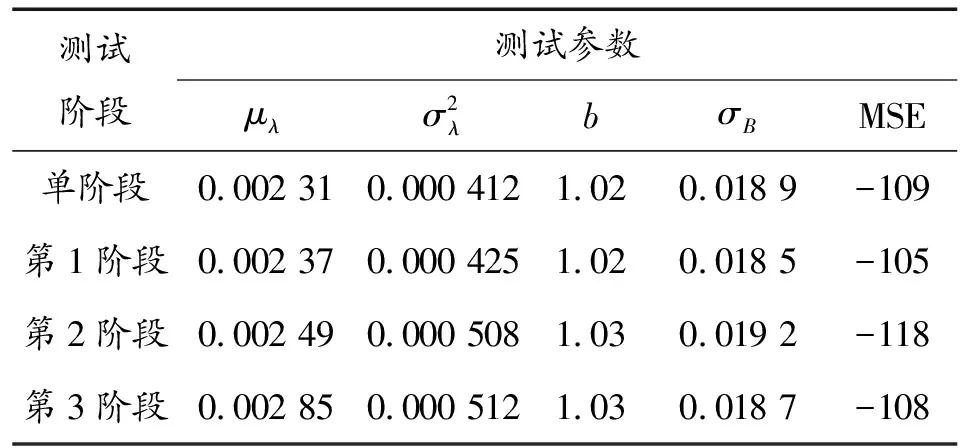
表3 不同階段模型參數的修正值

從表3可以看出多階段退化模型參數AIC的平均值小于單階段退化模型，證明本文的多階段參數估計方法更加精確，退化模型更加可靠。

最后利用修正后的模型進行剩余壽命預測，如圖2所示。選取工作時間3 000 h，計算多階段非線性模型和單階段非線性模型的平均剩余壽命，分別為2 362 h和2 721 h。而在退化試驗中，速率陀螺儀的平均失效時間為5 016 h。通過對比，本文所采用的基于Wiener過程的多階段非線性退化模型所預測的剩余壽命更加接近實際情況。

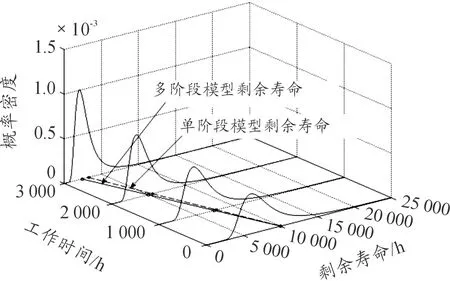
圖2 剩余壽命預測概率密度

5 結論

1) 本文采用基于非線性Wiener過程建立速率陀螺儀的退化模型，使用Gibbs采樣算法估計復雜模型的多個未知參數，并通過Kalman濾波算法進行漂移系數的修正，實現了退化過程的多階段性。

2) 退化試驗結果與不考慮漂移系數修正的單階段退化模型相比，多階段退化模型更加符合實際退化過程，對于剩余壽命預測更加準確。

3) 由于非實驗條件下采集到的數據少且無效數據較多，使Gibbs采樣算法計算精度降低。如何在樣本少、干擾多的情況下估計模型參數值，需進一步研究。