基于模型預測的制動能量回收策略仿真分析

張鑫康，杜常清，曹錫良

（武漢理工大學 現代汽車零部件技術湖北省重點實驗室 汽車零部件技術湖北省協同創新中心，武漢 430070）

中國大學生電動方程式大賽（FSEC）是一個由各大學車隊學生設計、制造一輛小型方程式賽車并進行競賽的全國性賽事[1]。對于沒有防抱死制動系統的方程式賽車，制動能量回收系統可以實現制動力的動態調節，提高賽車的制動效能和制動方向穩定性且提高能量利用率。而現行的乘用車有關法規對于方程式賽車并不適用。由此可見，對該賽事開發一種特定的制動能量回收系統有著較強的必要性和適應性。

近年來，國內外學者對此進行了大量的研究。文獻[2]采用加權最小二乘的控制分配方法設計了汽車下層控制器；文獻[3]提出了一種雙電機驅動再生制動模糊控制策略；文獻[4]從頻域的角度出發提出一種新的制動意圖識別方法；文獻[5]提出一種根據電機轉矩特性分配電動汽車前軸制動力的再生制動控制策略。

同時，各個大學車隊也都對制動能源回收系統進行著積極的研究和設計。文獻[6]和文獻[7]各自以不同的控制算法分別設計了并進行了仿真分析；

（1）保證各種工況下的制動效能和制動方向穩定性；

（2）在電池和電機的性能限制下，盡可能提高能量利用率；

（3）保證并優化踏板行程提高制動平順性。

本文將依據以上3個方法，使用某大學賽車的整車參數，基于模型預測控制算法，進行控制策略的仿真設計。

1 制動能量回收系統設計

1.1 制動能量回收控制方案分類與選擇

目前一般的制動能量回收策略可按照電制動力和機械制動力的耦合關系分為疊加式（并聯式）和協調式（串聯式），如圖1所示[8]。

圖1 能量回收策略分類Fig.1 Classification of energy recovery strategies

疊加式，也稱并聯式，機械結構和能源回收控制算法簡單可靠，實施方便，但能源回收效率不高。

協調式，也稱串聯式，其控制策略的復雜程度大，控制精度受傳感器工況和環境影響較大，且需要前后輪制動器的制動力可調，結構復雜。

由于方程式賽車沒有ABS系統，無法實現踏板與制動油路的完全解耦，只能夠通過平衡桿來調節前后制動力分配，總制動力無法在踏板行程不變的情況下隨制動強度調節，所以在制動過程中無法實現串聯式的控制策略。并聯式控制策略由于其可靠性，和不需要踏板與制動油路完全獨立的特點，目前更加適用于在大學生方程式賽車。但其仍有回收效率不高，制動平順性差的缺點，故先以并聯式回收策略為基礎，依據3個評價指標對于控制策略進行迭代優化。

1.2 制動受力分析

車輛在制動時，只考慮車輛縱向動力學特性時，整車受力如圖2所示[9]。

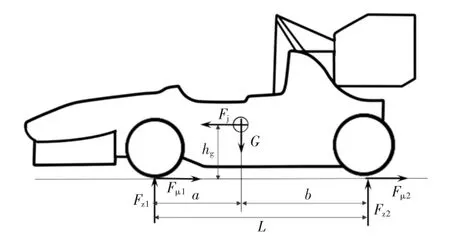
圖2 整車受力圖Fig.2 Force diagram of the vehicle

當制動過程中前后輪同時抱死時，設地面附著系數為φ，分別對前后輪與地面的接觸點力矩平衡方程，整理可得前后輪制動力關系方程：

基于本文研究的電動方程式賽車整車性能參數如表1所示，可以在Matlab中做出I曲線及β曲線，如圖3所示。

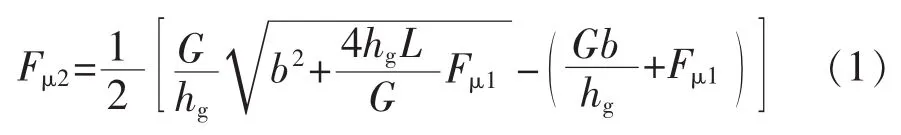
由式（1）可得前后輪同時抱死的理想制動力分配曲線，稱為I曲線，而在方程式賽車上前后輪的制動力分配通常由機械結構進行實現，通常以前輪制動器制動力與汽車總制動器制動力之比來表明分配的比例，稱之為制動器制動力分配系數，以符號β表示。

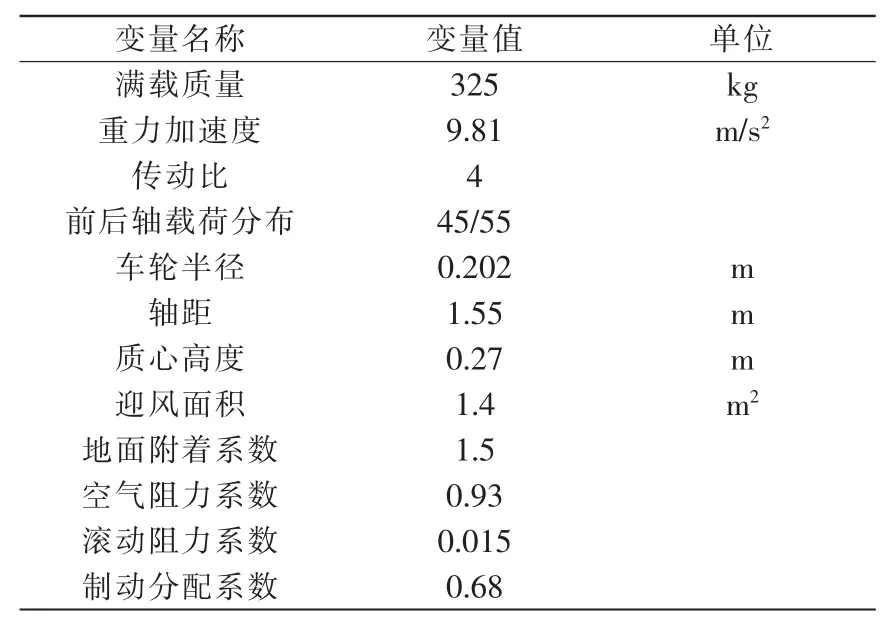
表1 WUTE方程式賽車隊刀鋒E5賽車參數Tab.1 WUTE formula racing team blade E5 racing parameters

1.3 電機制動參數計算

在設計制動能源回收算法時，需要計算電機的最大制動力矩，來保證回收算法的可行性。而電機的制動力矩是由電機的外特性曲線和電池的充放電特性一起決定的，在計算時還需要考慮電機的使用壽命和賽車特點。首先本文研究的賽車采用永磁同步電機，其外特性曲線在轉速較小時，電機輸出額定轉矩，當轉速較大時，電機以恒定額定功率輸出轉矩。

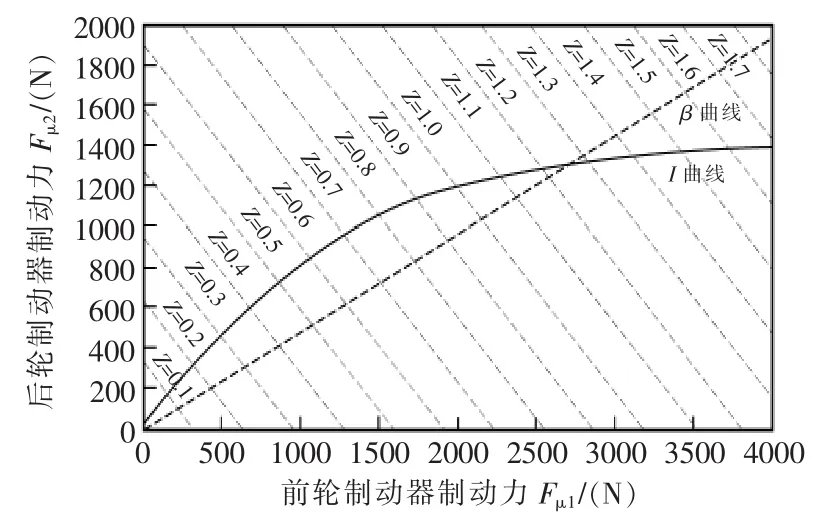
圖3 刀鋒E5的I曲線與β曲線對比Fig.3 Comparison of I curve andβcurve of blade E5

此外電池的充電倍率可以通過影響電機的最大功率來影響輸出轉矩特性，研究對象的電池參數如表2所示，其額定充電功率W可表示為

式中：C為充電倍率；Ah為電池額定容量；V為電池額定電壓。帶入表參數，可得電機最大充電功率為10.88 kW，由于始終以電池極限功率充電造成電池溫度升高，降低電池壽命，而賽規要求充電時不得大于2C，故最終限制電機最大充電功率為8 kW，又為避免在轉速較低時電機以較大功率輸入引發高溫，設置電機最大轉矩為75 N*m，則其制動轉矩外特性曲線如圖4。

1.4 基于規則的并聯控制策略設計

討論可行性時，策略首先要保證的是制動效能和制動方向穩定性，故基于I曲線對原有機械制動力進行修正。由于踏板位置與實際制動力受油壓影響較大，故本策略不以踏板位置作為輸入參數，而通過油壓傳感器來檢測前、后輪油路壓力作為輸入參數，對于制動力分配的控制更為準確。控制策略以并聯式混合制動系統的控制策略為基礎，結合賽車特點進行針對性設計，具體的控制邏輯如下：

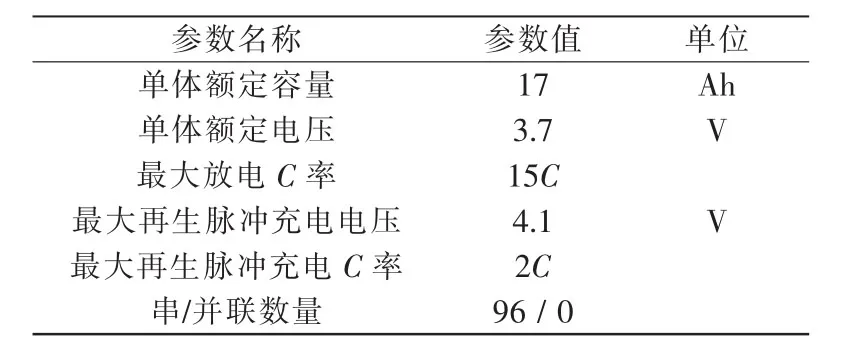
表2 聚合物鋰電池性能參數Tab.2 Performance parameters of polymer lithium batteries

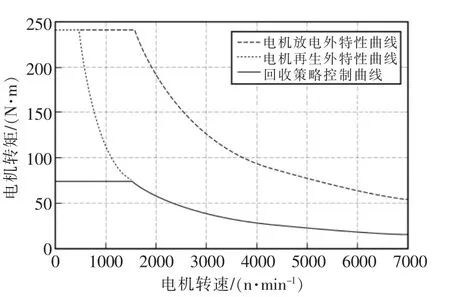
圖4 電機輸出制動轉矩特性曲線Fig.4 Output braking torque characteristic curve of motor

（1）當踏板行程處于前5%時，屬于輕制動強度階段，可以僅使用電機制動，通過踏板機械空程設計實現該階段不輸出機械制動力，電機以制動強度為0.1輸出制動力。由于制動強度不大，故僅以后輪制動依舊不會出現抱死現象。設此時后輪制動力為Fre；

（2）當踏板行程大于5%時，機械制動力開始緩慢增加，通過前輪油壓計算出基于I曲線的理想后輪需求制動力Fr，當Fr小于Fre時，為了保證制動平順性，使后輪制動力保持Fre不變，此時電機制動力等于Fre和后輪機械制動力的差值；

（3）當Fr大于Fre，同時后輪機械制動力小于Fr時，按照I曲線輸出制動力，此時電機制動力等于Fr和后輪機械制動力的差值；

（4）當后輪機械制動力大于Fr時，屬于緊急制動階段，不進行能量回收，此時電機輸出制動力為零。

基于以上控制策略，以下簡稱Case1，其對應的前后制動力關系如圖5所示，制動力分配如圖6所示。

1.5 基于模型預測的控制策略優化

為了優化現有控制策略的回收效率和踏板平順性，引入模型預測控制算法對于已有的控制策略進行優化。模型預測控制是一種基于模型的閉環優化控制策略，其思想核心為利用模型預測未來有限時域內的狀態參數并求解最優控制參數，并通過閉環結構進行滾動優化。該算法可以將復雜系統中的多個控制目標整合計算，并有計算效率高，魯棒性強的特點。故采用模型預測優化控制策略。該控制過程可分為3個部分，模型預測部分，最優求解部分，反饋優化部分。

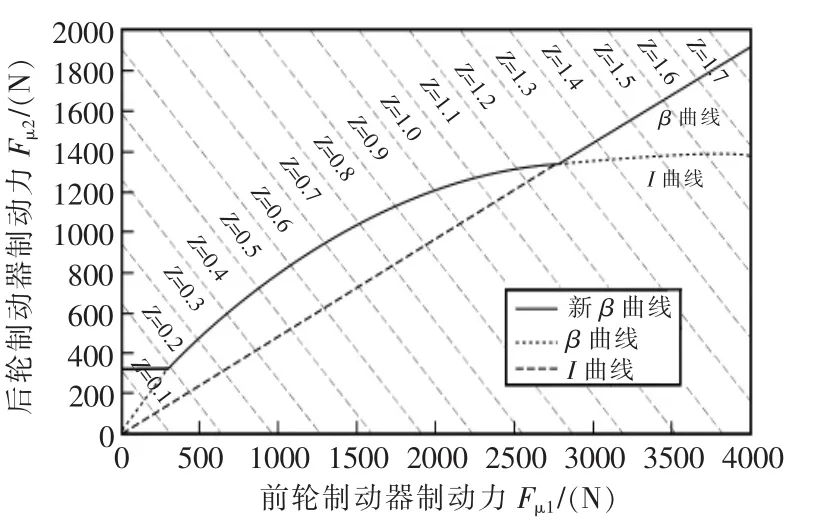
圖5 并聯式控制策略β曲線Fig.5 Parallel control strategyβcurve

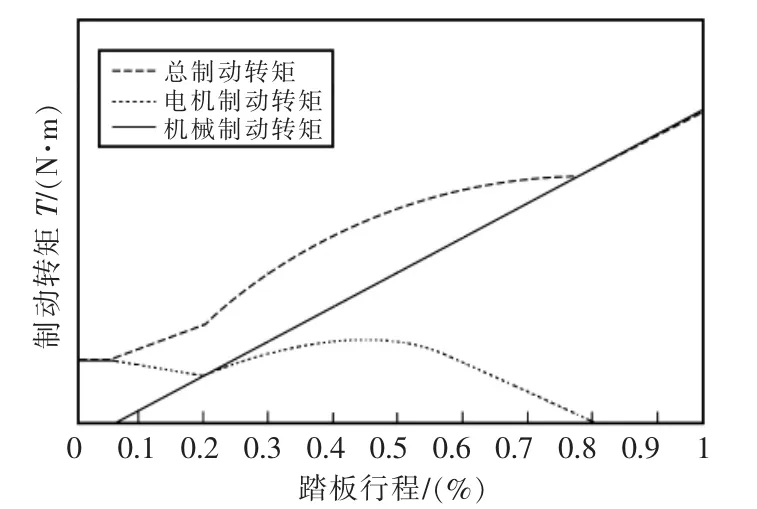
圖6 制動力分配示意圖Fig.6 Schematic diagram of braking force distribution

根據圖2和Case1可得前后車輪的動力學模型；

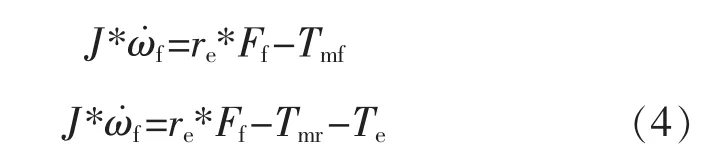
式中：J為輪胎轉動慣量；ω為車輪角速度（rad/s）；re為輪胎有效半徑（m）；Ff和Fr為前后車輪所受縱向力（N）；Tmf和 Tmr為前后輪機械制動轉矩（N·m）；Te為電機制動轉矩（N·m）。將模型離散化后得到系統的狀態方程：

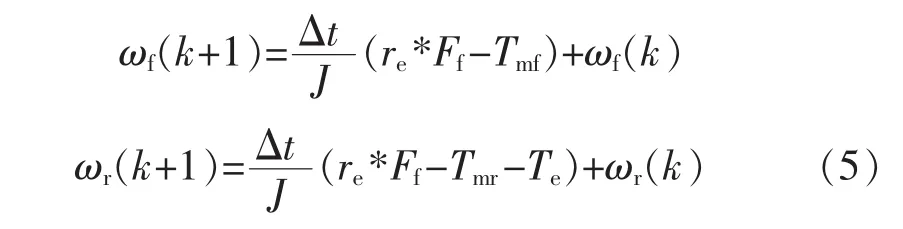
式中：Δt為離散時間間隔；選取前后車輪角速度為狀態變量，電機制動轉矩和前后輪機械轉矩為控制變量。

系統的目標函數依據3個評價方式建立，即基于制動強度，能量回收率和制動平順性分別建立J1、J2、J3三個目標函數：

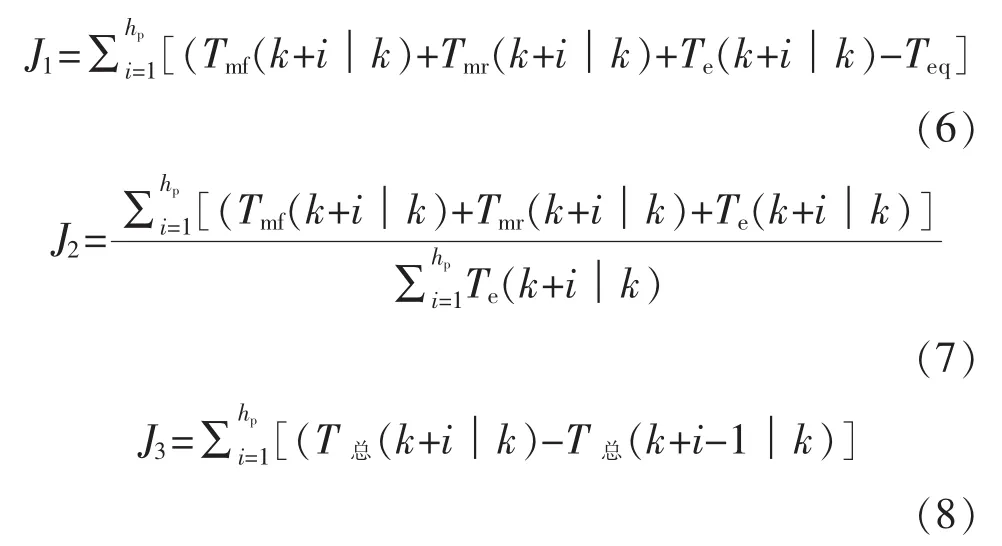
式中：T（k+i│k）為在 k時刻對 k+i時刻的預測值；hp為預測時域；Teq為根據踏板位置得出的需求制動總轉矩；T總為輸出機械轉矩和電機轉矩總和，故總目標函數為

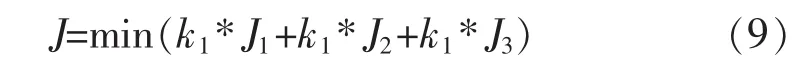
式中：k1、k2、k3為各目標函數的權重系數，根據車輛的運行狀態確定，在求解最優參數時還需設定邊界條件，根據整車機械結構限制和電機參數限制確定的邊界條件如下：

（1）Tmf與Tmr由平衡桿控制， 由于結構原因，二者比值范圍為［0.4，2］；

（2）總機械制動力只與車手施力有關，由油壓傳感器測得，在一個有限時域內按定值計算；

（3）為控制制動穩定性，將前后制動力限制在Case1的I曲線和β曲線之間來保證穩定性；

（4）電機輸出轉矩如圖4曲線確定范圍；

（5）由于電池的充電特性，在SOC大于90時，為了保護電池，不進行能量回收。

根據目標函數和邊界條件可以求解出每一瞬間有限時域內使目標函數最小的最優解，求出的其中前后制動轉矩以制動力分配系數的形式輸出，上述流程如圖7所示。以下簡稱Case2。

2 基于Matlab/Simulink整車模型仿真分析

2.1 基于車輛動力學的整車模型建立

根據車輛動力學理論可知，車輛在道路上行駛時，必須克服來自地面的滾動阻力和坡度阻力、來自空氣的空氣阻力、加速時由于慣性而產生的加速阻力，車輛的驅動力必須克服這些行駛阻力才能使汽車在道路上正常行駛。為便于分析，本文以簡化為線性二自由度的車輛模型進行建模和分析，建立車輛行駛方程式為

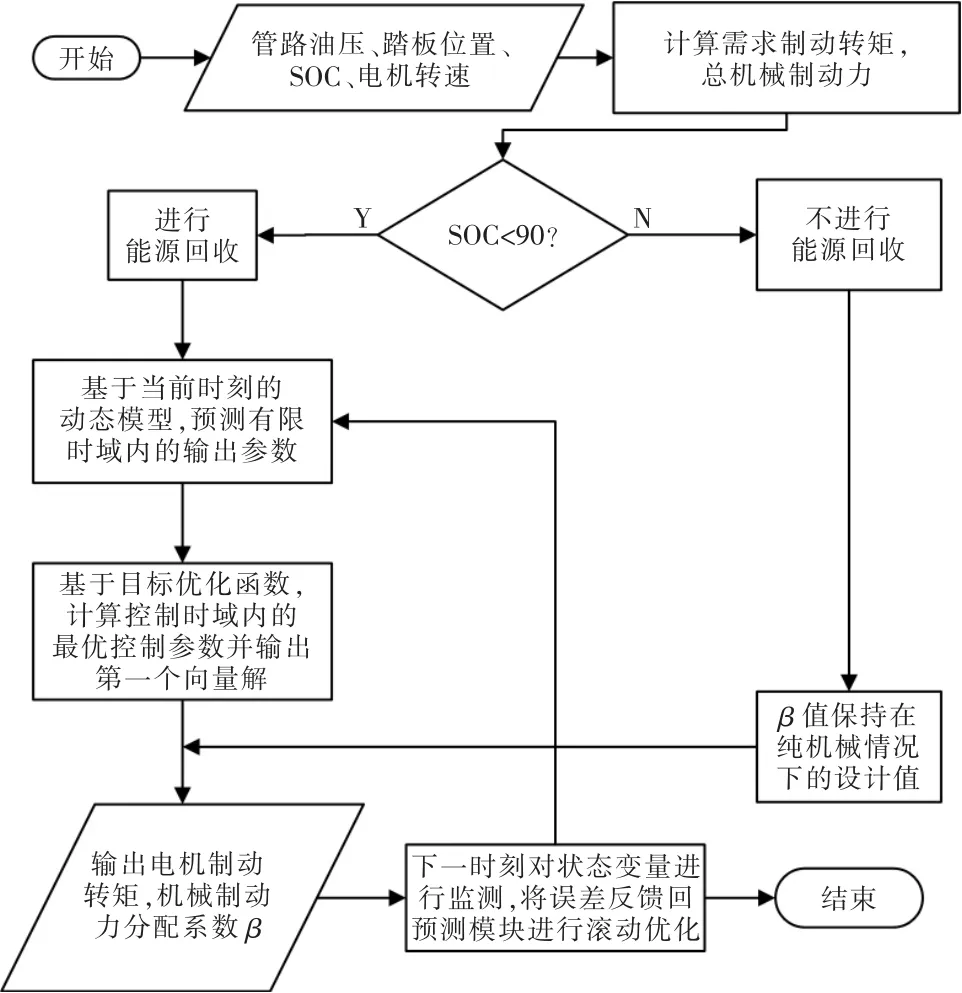
圖7 模型預測控制流程Fig.7 Model predictive control flow chart

式中：Ft為車輛行駛時的驅動力（N）；Ff為車輛行駛時的滾動阻力（N）；Fw為車輛行駛時的空氣阻力（N）；Fi為車輛行駛時的坡度阻力（N）；Fj為車輛行駛時的加速阻力（N）。

依據車輛行駛方程式，利用Simulink的Simscape工具建立整車模型，將整車模型分為車身及底盤子系統，電機驅動子系統和駕駛員子系統，基于刀鋒E5整車參數對3個子系統進行建模。

2.1.1 車身及底盤子系統

車身及底盤子系統如圖8所示，該子系統分為三大模塊，brake模塊為車輛機械制動系統模型，接收駕駛員的制動信號，向兩輪輸出制動轉矩，Vehicle模塊為車身及基于魔術公式的兩輪模型，接收制動轉矩和后輪的電機轉矩，輸出整車的瞬時縱向總力，并利用slip對前后輪的滑移率進行監控，Speed&Distance模塊是用于計算整車的瞬時速度和行駛里程的模塊。

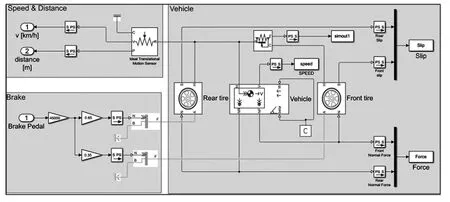
圖8 車身及底盤子系統模型Fig.8 Body and chassis subsystem model

2.1.2 電機驅動子系統

電機驅動子系統如圖9所示。通過接收駕駛員的加速信號和電機的外特性曲線，利用Simscape的PMSM永磁同步電機等模型建立電機控制模塊，輸出瞬時電機減速后的驅動轉矩，將賽車的電機、池及傳動比參數帶入到模型中。

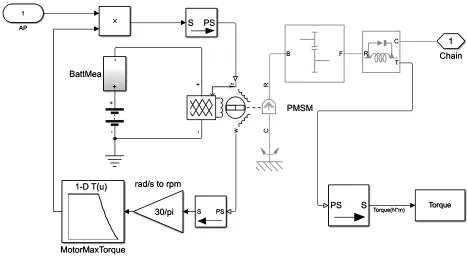
圖9 電機驅動子系統模型Fig.9 Motor drive subsystem model

2.1.3 駕駛員子系統

駕駛員子系統是通過將輸入的目標車速與實際車速對比，通過駕駛員PID反饋調節模型進行控制，輸出制動或加速信號來達到對整車控制的目的，模型如圖10所示。

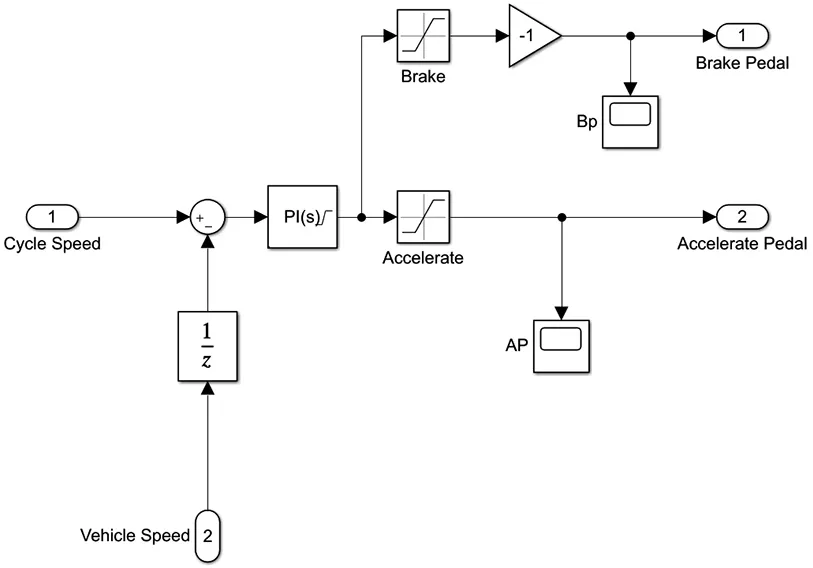
圖10 駕駛員子系統模型Fig.10 Driver subsystem model

2.1.4 整車模型建立

將3個子模型進行連接，利用scope檢測車速，行駛里程，并對目標車速和實際車速進行對比，利用Drive Cycle Source模塊完成對目標車速的輸入，如圖11所示。

2.1.5 整車模型驗證

整車模型建立完成后，需對模型的正確性進行實驗驗證，該整車模型需從物理模塊與駕駛員模塊分別進行驗證。

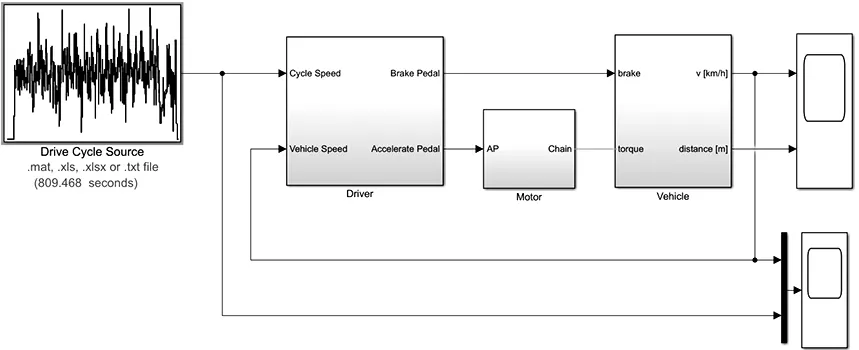
圖11 整車系統模型Fig.11 Vehicle system model

物理模型部分通過進行制動測試工況和直線加速工況仿真實驗對比來驗證正確性。在制動測試工況時，駕駛員先要逐漸加速3～4 s，之后全力制動，要求四輪同時抱死且制動距離不超過5 m。直線加速工況是指駕駛員在賽車零初始車速時加速通過75 m直線路段的工況，以所用時間記為比賽成績。故輸入模擬上述2種工況的駕駛員信號，得出仿真的車速和行駛里程。通過實車實驗，可得制動距離與加速時長，如表3所示。

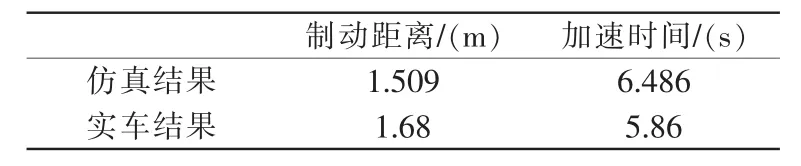
表3 整車模型與實車測試數據對比Tab.3 Comparison of vehicle model and real vehicle test data

駕駛員部分通過耐久工況目標與實際車速對比來驗證。截取耐久工況前100 s目標車速與模型實際車速對比，如圖12所示。

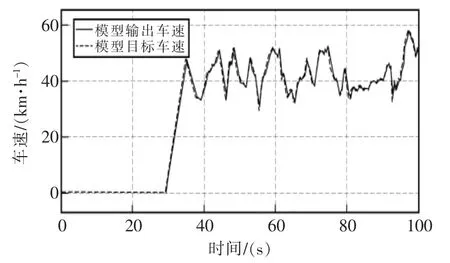
圖12 模型車速對比Fig.12 Model vehicle speed comparison

2.2 制動能量回收系統模型搭建

由于本文設計能源回收控制策略以并聯式為基礎，故可只對整車模型的制動模塊和電機控制模塊進行修改。在駕駛員和整車模型中間添加模型預測（MPC）控制模塊，輸入信號由駕駛員的制動信號判斷目標制動強度，輸入SOC值判斷回收程度，依據Matlab的模型預測和最優求解程序輸出β和電機制動力矩，并將模型的前后車輪角速度反饋回MPC模塊對預測模型進行滾動優化。由于底盤子系統中的制動模塊與其他系統交互較多，故將制動模塊另拆分為獨立的子系統，如圖13、圖14所示。

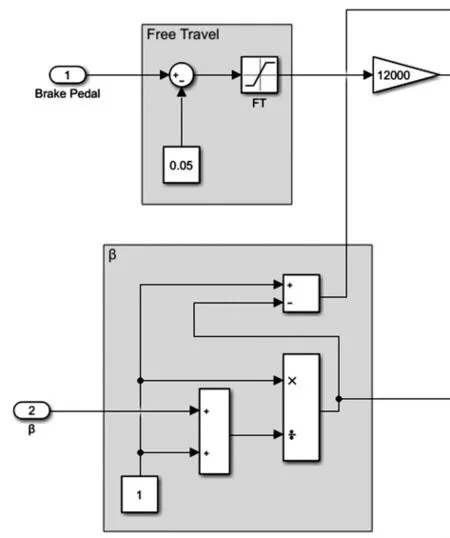
圖13 車身及底盤子系統模型Fig.13 Body and chassis subsystem model

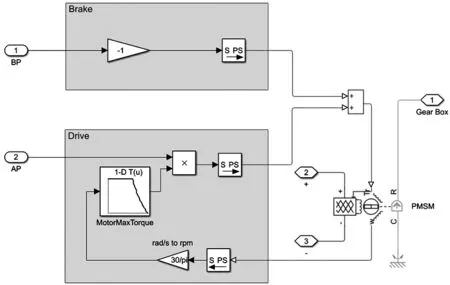
圖14 搭載能量回收的電機控制系統模型Fig.14 Model of motor control system with energy recovery

加入MPC制動能源回收系統的整車模型如圖15所示。

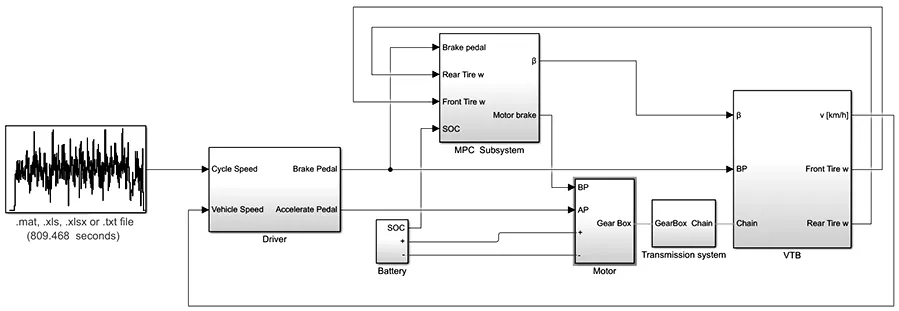
圖15 模型預測控制整車系統模型Fig.15 Model predictive control model for vehicle system

2.3 基于Simulink的控制策略有效性仿真對比

本文所使用的行駛循環工況數據來自2017年中國大學生電動方程式大賽耐久與效率測試賽道。因其耐久賽分為上下兩部分，中間間隔2 min左右，上下兩部分行駛路程相同，為了驗證液力協調式控制策略的有效性，利用賽車參加17年耐久賽前半部分賽車中車速傳感器所采集的車速數據作為目標車速，與不搭載制動能量回收系統的模型，搭載一般并聯式能量回收系統的模型進行比對，通過比對電池的SOC值來驗證回收策略的有效性。其輸入車速曲線如圖16所示。

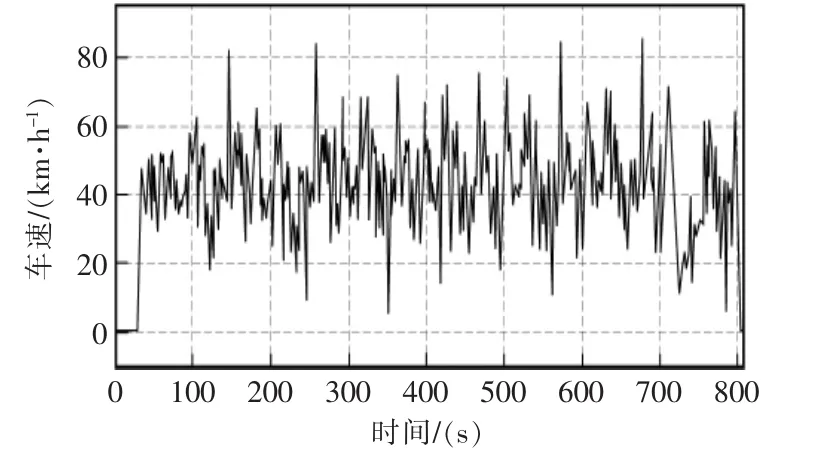
圖16 耐久賽工況目標車速曲線Fig.16 Target speed curve for durable race conditions

通過Simulink仿真，可以得出整車動力學和電量狀態的仿真結果，在電池處加入BatMea模塊用于檢測電池的瞬時電流和SOC值。方法為利用電流傳感器記錄電流值，篩選為充電電流和放電電流兩部分，對于兩部分分別積分，再與賽車電池總容量相加，可得出電池瞬時SOC值曲線，對比基于模型預測的控制策略與普通并聯式和無能量回收的模型的SOC曲線，如圖17、圖18所示。

通過上述曲線可得，采用基于模型預測的回收策略的模型在半程耐久項目之后電池剩余SOC值為62.9%，而采用普通并聯式的SOC值為58.8%，無能源回收系統的模型SOC值為55.7%。可以看出，協調式制動能量回收控制策略比普通并聯式的相對耗電量減少4.1%，比無制動能量回收系統的情況減少7.2%。除此之外還可以用能量回收率ηreg來評價制動能量回收系統的回收效率[10]，令：

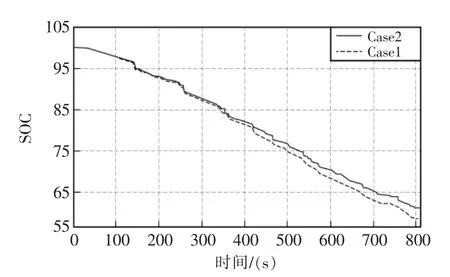
圖17 模型預測算法與并聯式控制策略SOC曲線對比Fig.17 Comparison of SOC curves between model prediction algorithms and parallel control strategies

圖18 模型預測算法與無能量回收策略SOC曲線對比Fig.18 Comparison of SOC curve between model prediction algorithm and energy-free recovery strategy

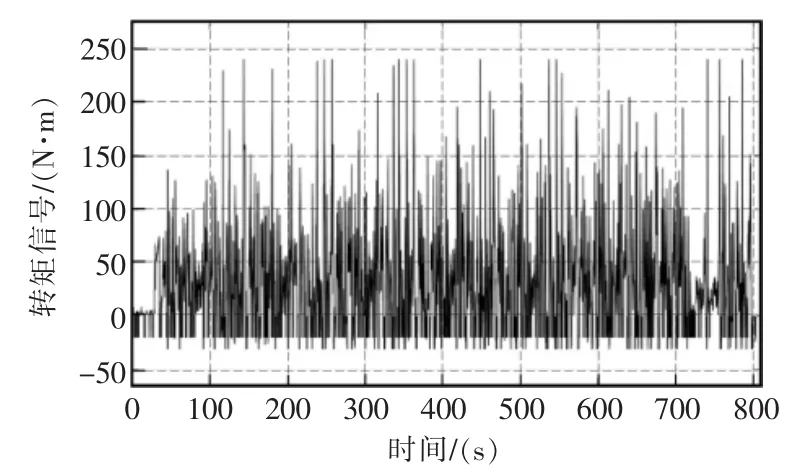
圖19 協調式電機輸出轉矩曲線Fig.19 Output torque curve of harmonized motor

式中：Ereg為測試全程制動回收的總能量，通過將充電電流延時間積分算出；Ebrk為制動過程中的總能耗，為前輪制動能耗 Eμf，后輪制動能耗 Eμr，電機制動能耗Eμm之和，三者的表達式如下。

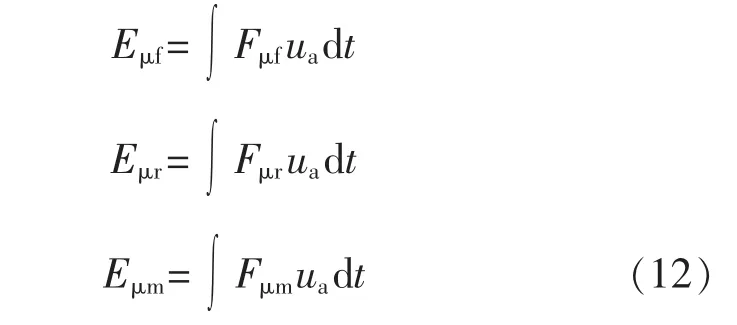
通過在Simulink模型的制動部分和電機控制部分插入相應的計算模塊，可得出前輪制動能耗Eμf，后輪制動能耗 Eμr，電機制動能耗 Eμm在 3 種模型下的結果，結果如表4。

由此可見，基于模型預測的控制策略可以達到30.4%的能量利用率，比普通并聯式控制策略能量利用率提高了9.4%，證明了該控制策略更優越的能源回收效率。

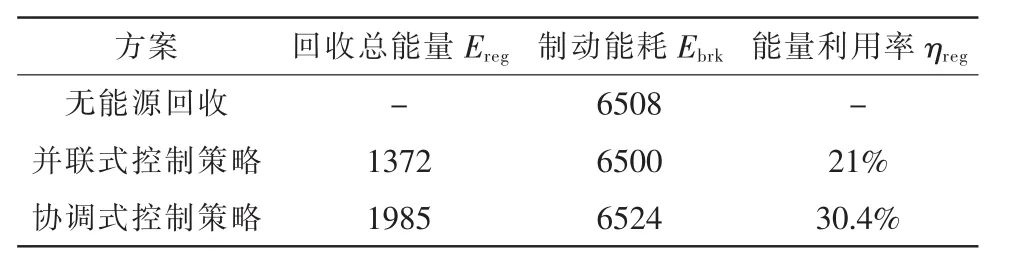
表4 能量利用率仿真數據對比Tab.4 Comparison of simulation data on energy utilization

2.4 基于Simulink的控制策略可行性仿真對比

對于新型的控制策略，我們不僅需要評價策略的回收效率，還需要評價其的制動效能和制動方向穩定性，以確保制動策略的安全性。現以大賽緊急制動時的工況來測試其制動效能。在該工況下，賽車以0 km/h的汽車車速逐漸加速，在經歷5 s的加速時間后緊急制動，檢測賽車的制動距離，和前后輪滑移率，對比基于模型預測的控制算法、普通并聯式控制算法和未搭載能源回收的賽車模型在同一駕駛員數據下對比其車速和制動距離隨時間的曲線，結果如圖20所示。

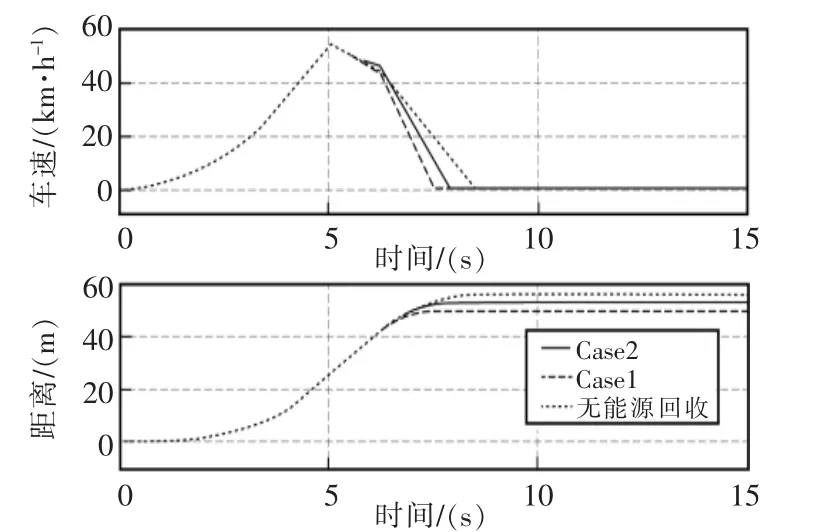
圖20 車身及底盤子系統模型Fig.20 Body and chassis subsystem model

由圖可知，基于模型預測的控制算法、普通并聯式控制算法和未搭載能源回收的賽車3種方案的制動距離分別為27 m，25.8 m和31.5 m，由結果可知搭載了制動能源回收系統的模型由于更全面地利用了地面附著率，有效地縮短了制動距離，提高了制動效能和制動方向可靠性，而經過仿真發現基于模型預測的控制算法的制動距離要比并聯式控制算法的制動距離長，其原因是在制動強度小于地面附著率時，基于模型預測的控制算法會考慮回收率和踏板平順性，將前后制動力分配在I曲線和β曲線之間，而此時并聯式控制算法會按照I曲線制動，總制動力會大于基于模型預測算法的制動力，故基于模型預測算法的制動效能的優化程度會小于并聯式控制算法的優化程度。

3 結語

對比了乘用車和大學生方程式賽車的工況特點，總結了適用于大學生方程式賽車的制動效能，能源回收率，踏板平順性3個評價方式。并基于模型預測控制設計了具有一定針對性的能量回收控制策略。

基于某方程式賽車的整車參數，利用Matlab/Simulink建立了整車動力學模型和制動能源回收控制算法模塊，基于大學生方程式大賽耐久賽的車速數據，對基于模型預測的控制算法和普通并聯式控制算法進行了有效性比較，得出基于模型預測的控制策略可以達到30.4%的能量利用率，比普通并聯式控制策略能量利用率提高了9.4%，證明了該控制策略更優越的能源回收效率。

通過對控制算法的Simulink模型進行單次緊急制動工況仿真，對比了模型預測控制算法和普通并聯式控制算法以及不搭載制動能源回收系統的模型的速度曲線和制動距離曲線，發現搭載了基于模型預測的控制算法的模型制動距離比未搭載能源回收的模型的制動距離減少了4.5 m，有效的優化了制動效能，證明了控制策略的可行性。