基于差分法的高溫作業專用服裝設計
李俊豪

摘要:隔熱防護服對在高溫條件下的工作人員起著至關重要的防護作用,它通過阻擋部分熱量的傳入而保護人體不被灼傷。通過從2018年高教社杯全國大學生數學建模大賽A題數據出發,立足于基礎傳熱學、熱力學相關理論,采用數據擬合、差分、有效假設、數據處理等手段,使用SPSS、MATLAB等編程軟件與數據處理軟件,構建了一維非穩態熱傳導方程的數學模型,得出了相應溫度條件下要求的隨著時間變化隔熱服的溫度分布變化,為隔熱防護服的設計提供合理化建議。
關鍵詞:一維非穩態熱傳導方程式;差分法;MATLAB;SPSS
中圖分類號:TS941.2
文獻標識碼:A
DOI: 10.15913/j.cnki.kjycx.2019.11.047
專業防護服裝是高溫環境工作下人們的重要保護工具。它由三層針織材料構成,與外界環境接觸的稱為I層,依次向里稱為II層、in層、III層與皮膚之間的空氣層稱為IV層。合適的防護服對于工作人員來說不但可以保證安全,也減輕了負擔,因此設計出好的防護服是當務之急。而防護服的性能效果與厚度等眾多影響因素都有著密不可分的關系。
為了設計專用服裝,通常實驗將體內溫度控制在37℃的假人放置在實驗室的高溫環境中,測量假人皮膚外側的溫度。為了降低研發成本、縮短研發周期,本文根據2018年高教社杯全國大學生數學建模大賽所提供數據,基于環境溫度75℃、工作時間90min、人體體溫37℃這樣的起始條件,建立數學模型,計算出理論上90 min內該防護服的溫度分布變化,以期為防護服制造商提供合理化建議。
1 數據來源
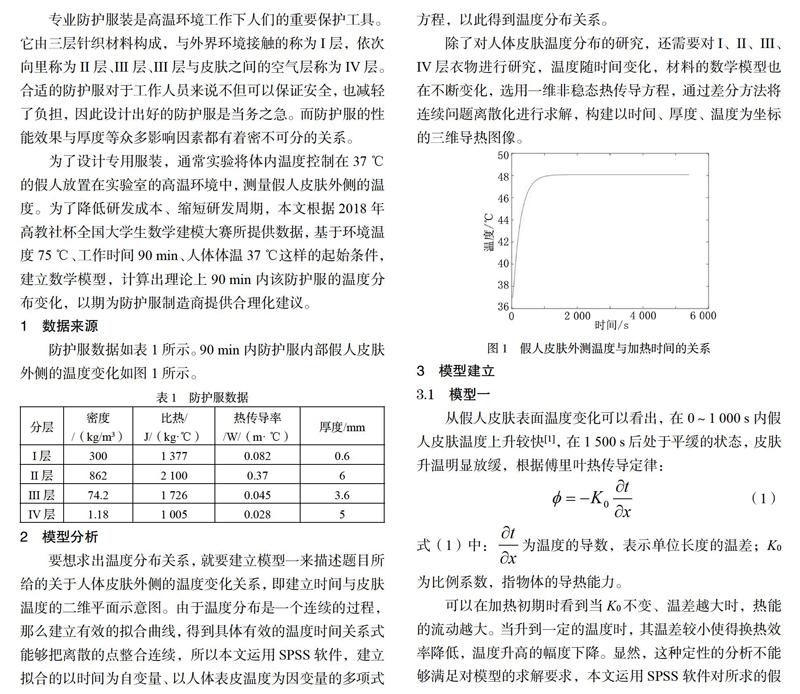
防護服數據如表1所示。90 min內防護服內部假人皮膚外側的溫度變化如圖1所示。
2 模型分析
要想求出溫度分布關系,就要建立模型一來描述題目所給的關于人體皮膚外側的溫度變化關系,即建立時間與皮膚溫度的二維平面示意圖。由于溫度分布是一個連續的過程,那么建立有效的擬合曲線,得到具體有效的溫度時間關系式能夠把離散的點整合連續,所以本文運用SPSS軟件,建立擬合的以時間為自變量、以人體表皮溫度為因變量的多項式方程,以此得到溫度分布關系。
除了對人體皮膚溫度分布的研究,還需要對I、II、III、IV層衣物進行研究,溫度隨時間變化,材料的數學模型也在不斷變化,選用一維非穩態熱傳導方程,通過差分方法將連續問題離散化進行求解,構建以時間、厚度、溫度為坐標的三維導熱圖像。
3 模型建立
3.1 模型一
從假人皮膚表面溫度變化可以看出,在0-1 000s內假人皮膚溫度上升較快[1],在1 500 s后處于平緩的狀態,皮膚升溫明顯放緩,根據傅里葉熱傳導定律:
可以在加熱初期時看到當Ko不變、溫差越大時,熱能的流動越大。當升到一定的溫度時,其溫差較小使得換熱效率降低,溫度升高的幅度下降。顯然,這種定性的分析不能夠滿足對模型的求解要求,本文運用SPSS軟件對所求的假
由此可見,熱阻與導熱系數成反比,而根據導溫系數與導熱率(導溫系數)的關系,其成正比時,導熱系數越大,導溫系數越大[4],因此,不妨大膽得出熱阻θ與導溫系數α成反比,并且根據這種關系可以推導出串聯的多層平壁式結構復合導溫系數:
將串聯導溫系數ao導人差分方程,運用MATLAB軟件進行數據處理可以建立以下圖像,該多層平壁式結構的總溫度與時間的變化圖像如圖2所示。
3.3 模型三
根據所建立的模型二,使用MATLAB軟件進行數據的處理計算,并根據表達方程建立圖像,得到各層材料中溫度隨時間的變化。其中第一層材料中溫度隨時間變化的圖像如圖3所示。
圖3中,x軸為材質厚度,t軸為時間變化,T軸為溫度,圖中清晰可見溫度的變化[1],完全符合傅里葉熱傳導定律,即隨著時間的延長,物體表面溫度升高使物體本身與外界的溫差變小,傳熱效率逐漸降低,且隨著傳熱距離的加長,其溫度變化的物體傳熱的速度變慢,導溫效率明顯下降[5],可以看到熱方程的解具有初始溫度平滑化的能力,這也就表明高溫一定會向低溫進行傳播,在初始狀態有一定區別的情況下會逐漸趨于穩態,改變原有的初始狀態。
4 結論與建議
通過使用MATLAB、SPSS進行模型構建,并使用差分法進行模型求解,本文最終得到了不同層的防護服在特定條件下的溫度變化,同時給出了對于相同問題求解的統一性解決方案,創新性地提出了定量式的研究方法,為廣大防化服制造商找到能夠使用模型預測防化服溫度的模型方案,在數學物理方向中作出了獨特的貢獻。
參考文獻:
[1]俞昌銘.熱傳導及其數值分析[M].北京:清華大學出版社.1981.
[2]陶文銓,楊世銘.傳熱學[M].4版.北京:高等教育出版社.2006.
[3]徐定華,陳遠波,程建新.低溫環境下紡織材料類型設計反問題[J].紡織學報,2011(9):24-28.
[4]劉麗英.人體微氣候熱濕傳遞數值模擬及著裝人體熱舒適感覺模型的建立[D].上海:東華大學,2002.
[5]徐定華,葛美寶,陳瑞林.基于服裝舒適性的紡織材料涉及反問題[J].應用數學與計算數學學報,2012(3):332-341.
[6]余躍.紡織材料熱濕傳遞數學模型及其設計反問題[D].杭州:浙江理工大學,2016.

