基于改進參數的粒子群算法的換熱網絡優化

周 靜，崔國民，彭富裕，肖 媛

（上海理工大學 新能源科學與工程研究所，上海 200093）

換熱網絡在現代工業生產過程起著舉足輕重的作用，特別是在石油化工、能源動力、低溫工程等［1］對能源需求相對較大的領域，為降低產品成本和節約能耗對其進行綜合優化具有重要的意義［2］。20世紀70年代開始，換熱網絡綜合優化逐步發展成為新時期的熱點問題，產生了一系列優化設計換熱網絡的方法。對于換熱網絡中的連續變量，通常采用確定性方法進行優化［3］。但由于換熱網絡優化問題具有嚴重的非線性和非凸特性，導致局部最優解太多，而確定性方法的優化結果不能保證可以找到全局最優解。

近年來，通過模擬自然界生物的群行為構造隨機優化算法的思想迅速發展，使得啟發式方法更加多樣化［3］。粒子群算法［4］作為其典型的方法之一，采用模擬鳥群飛行覓食行為的方法，通過鳥之間的集體協作使群體達到最優。但其在換熱網絡中的應用相對較少。嚴麗娣等［5］利用粒子群算法對換熱網絡進行優化，取得了較好的結果。

本文通過對嚴麗娣等［5］提出的粒子群算法優化換熱網絡的策略進行改進，對算法中參數的取值進行調整，使算法具有更好的全局收斂性能。

1 換熱網絡優化數學模型

1.1 換熱網絡綜合問題的表述

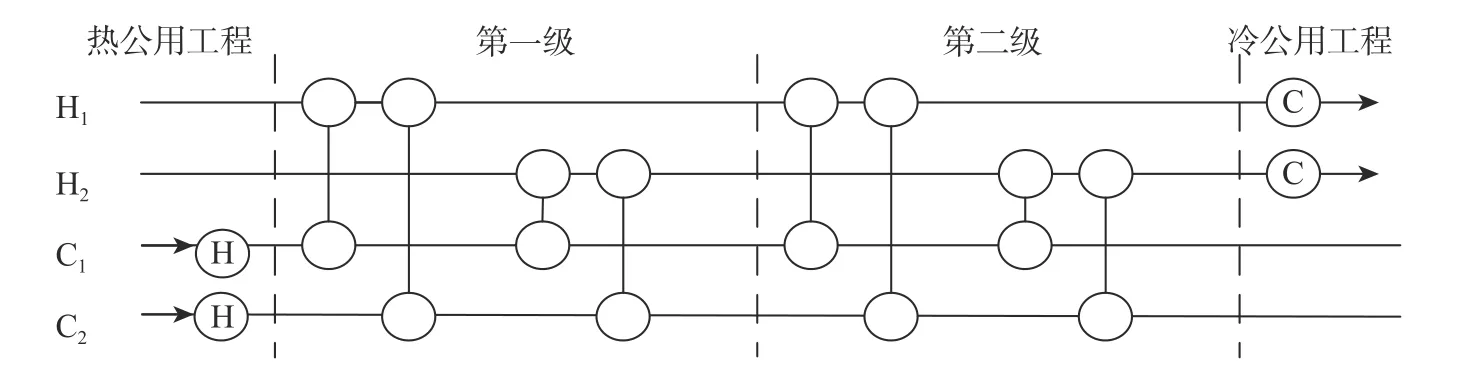
圖1 4股流體換熱網絡分級超結構Fig.1 Stage-wise superstructure of heat exchange network with 4 streams

1.2 優化的目標函數

傳統的換熱網絡綜合優化時是以換熱網絡性能，即年綜合費用F為目標函數，F主要包括面積投資費用和公用工程費用，通常以此作為評價換熱效率的指標［7］。面積投資費用包括換熱器固定投資費用、面積費用；公用工程費用包括冷、熱公用工程費用。

以F最小為優化目標，其數學描述為

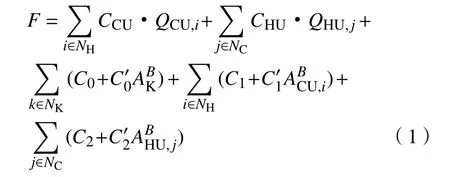
計算單個換熱器時，同時要求換熱的冷、熱流股之間滿足

2 粒子群優化算法實現步驟

粒子群算法的發展始于1995年Kennedy和Eberhart［4］提出的基本粒子群算法。其中基本粒子群算法的參數是固定的，這使得優化函數時精度較差。以圖1中的4股流體為例，闡述粒子群算法在換熱網絡中的實現。該算法的具體步驟為：

（1）設定種群大小和最大迭代次數，種群中每個粒子代表換熱網絡的一個結構，粒子各維度下的值代表每個結構中各換熱器的換熱面積。

（2）設初始換熱器面積取值為 (0,5)，初始種群大小為N，每個粒子含有d個換熱器，則這N組d維優化變量（換熱面積）為xi=(xi1,xi2,···,xid)=rand()× 5,i=1、2、···、N。N組d維粒子速度為vi=(vi1,vi2,···,vid)=rand()。rand()是介于 (0,1)之間的偽隨機數。

（3）種群中各粒子按照式（3）、（4）依次改變換熱器面積及飛行速度，即

（4）若未滿足最大迭代次數，則重復步驟（3），循環計算。在為1 000次后跳出，記錄最優的換熱網絡面積及換熱網絡最小年綜合費用。

3 粒子群算法中控制參數的改進

選取嚴麗娣等［5］論文中的一個考慮固定投資的4sp2算例為例，表1為算例4sp2物流參數，其中：Ti、To分別為流體進口、出口溫度；MCp為流體熱容流率。在其論文中，通過對夏濤等［8］提出的運用粒子群算法求解換熱網絡思路的改進，對換熱網絡進一步優化，得到了最小年綜合費用為124 670$·a-1的優化結果。但其改進的過程沒有具體的實現步驟，本文對粒子群中參數進行改進，使其能夠搜索到更優的解。計算中，換熱器、冷卻器的傳熱系數均為0.8 kW·m-2·℃-1，加熱器的傳熱系數為1.0 kW·m-2·℃-1，加熱器價格公式為8 600 +1 200A0.6$·a-1，其中A為換熱器的面積，其他換熱器價格公式為8 600 + 1 000A0.6$·a-1。加熱公用工程價格和冷卻公用工程價格分別為80、20$·kW-1·a-1。

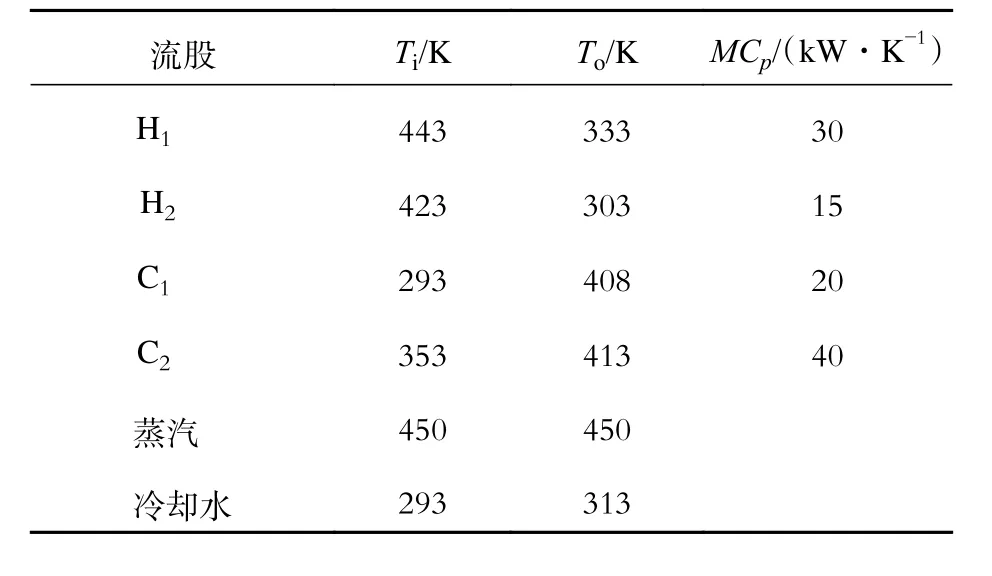
表1 算例4sp2物流參數Tab.1 Material flow parameters of case 4sp2

由于標準粒子群算法中參數固定，優化時往往達不到理想效果，因此對參數進行調整是有必要的。但不同于其他算法，粒子群算法中需要調整的參數較少，主要包括：慣性權重ω；最大飛行速度限制[-vmax，vmax]；學習因子c1、c2；種群大小N；迭代次數k。

在換熱網絡的優化過程中，種群大小和迭代次數對優化結果影響不大，但取值都不宜過小，取適中值（N= 100，k= 1 000）。下面重點分析慣性權重ω、最大飛行速度vmax、學習因子c1和c2。在標準粒子群算法中，ω= 0.5，c1=c2=2.0。將這三個固定取值的參數運用到4sp2的換熱網絡中進行優化，得到的最小年綜合費用為130 283$·a-1。

3.1 慣性權重

雖然粒子群算法應用于換熱網絡的搜索過程是非線性的復雜過程，式（5）中從全局搜索到局部搜索的線性變化并不能真實地反映搜索全局最優過程，但在換熱網絡優化的問題上，動態變化的對算法性能的增強起到較大作用。

3.2 學習因子和最大速度

由于粒子群算法中沒有實際的機制控制粒子速度，所以有必要對速度最大值進行控制。設置速度閾值為。 該參數被證明是非常重要的，因為值太大會導致粒子跳過最優解，太小的話又會導致對搜索空間的不充分搜索［10］。

1999 年 Clerc［11］證明為確保粒子群算法收斂，有必要使用收縮因子。將使用的粒子群算法（PSO）與使用收縮因子的PSO進行比較，粒子速度更新為

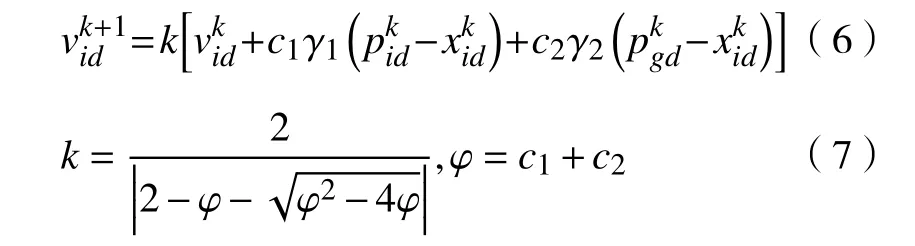
Clerc［11］的結論表明，為使PSO性能最好，有兩種方法：①使用收縮因子，且使vmax=xmax；②使用，取 ω=0.729，c1=c2= 1 .494 45。本文將結合以上結論，取c1=c2=1.494 45，仍采用線性遞減形式，vmax采用換熱網絡優化中不會引起面積爆炸的一個較大值，vmax=1 000。實際上，式（3）、（4）與式（6）、（7）中參數的選取是相通的。

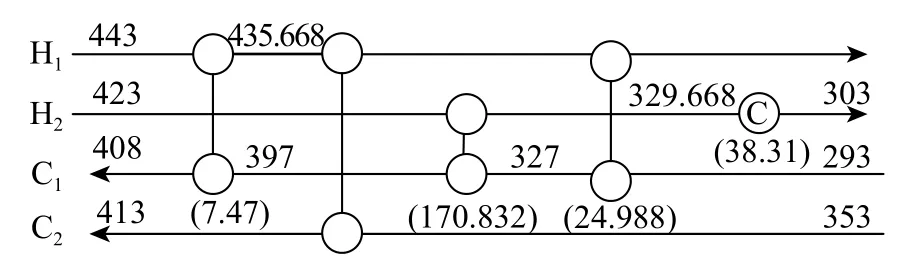
圖2 算例4sp2最優換熱網絡結構Fig.2 Optimum heat exchange network of case 4sp2

將上述的參數選擇逐步運用到4sp2的換熱網絡綜合優化中，得到換熱網絡最小年綜合費用對比如表2所示。由表中可以看出，對標準粒子群算法中的固定參數進行調整是有效的，改進后的粒子群算法具有更好的全局搜索能力。

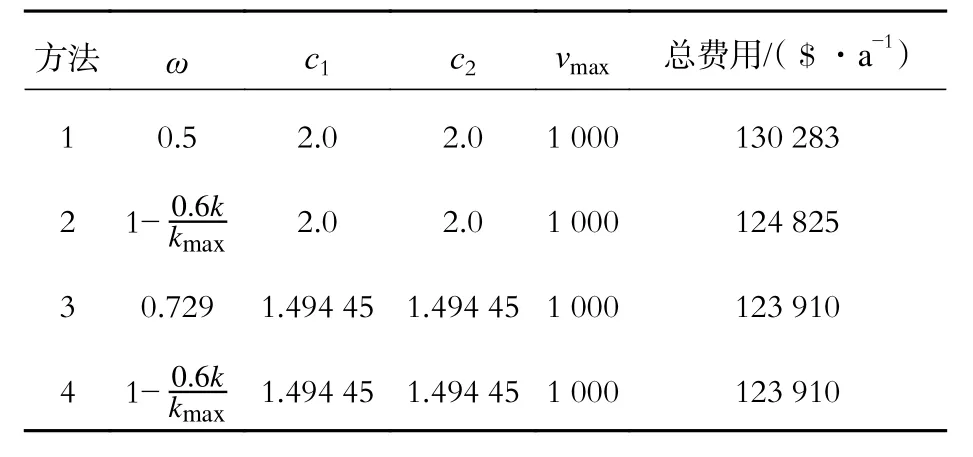
表2 算例4sp2結果比較Tab.2 Comparison of the results from case 4sp2

4 結 論

（1）在將標準粒子群算法應用于無分流換熱網絡模型的基礎上，對其中的參數、、、進 行調整、改進，通過逐步分析將標準粒子群算法中固定的參數調整為合適的值，使該算法對全局和局部探索能力更加平衡。

（2）利用一個4股流體算例驗證參數改進后的計算效果，可知改進后的算法具有更好的全局搜索能力。與標準粒子群算法得到的年綜合費用130 283$·a-1相比，最終改進后的費用為123 910$·a-1，降低了6 373$·a-1。