一種基于空氣密度的調節風機切入的新機制

鄧永華 姜慶云

摘 要：風力發電機的自動控制水平是風機效率和可靠性的重要指標之一。目前的風機一般只將風速作為風機切入的判斷條件。事實上，風機在運行過程中，風速切入主要由空氣密度和風速的三次方的乘積決定。本文根據風能捕獲和空氣密度相關的思想，提出了空氣密度調節的風機切入機制。這種機制在近乎零成本的投入下，可在低風速風場提高發電量約0.5%。

關鍵詞：空氣密度;切入風速;發電量

中圖分類號：TM614 文獻標識碼：A 文章編號：1003-5168（2019）02-0038-03

A New Improving Energy Product Model of Modulating?Wtg Cut-In Wind Speed by Air Density

Abstract： Automatic control represents one of the most important factors responsible for the efficiency and reliability of wind power conversion systems. Thus far， only the wind speed is considered as cut-in control mechanism. In fact， the cut-in requirement is determined by the ρv3， i.e. the air density times the cube of incoming wind speed， so the air density should be considered as the cut-in parameter. Based on this concern， a new model was suggested that the cut-in speed was modulated by the instant air density. This model can improve the energy product about 0.5% without any hardware cost at low speed wind farm.

Keywords： air density;cut-in wind speed;energy product

1 研究背景

風機切入風速的設定是檢驗風機質量的重要參數。現代風機電器系統大多采用變速恒頻運行方式，同時不斷追求最大的風能捕獲（Maximum Power Point Tracking，MPPT）。李晶[1]、姚駿[2]、趙仁德[3]等提出了多種實現最大風能跟蹤的控制方法，但缺乏對切入風速變化本身的關注。早些年，人們都將切入風速設定為相對較高的數值，因為早些年高風速風場居多，低風速階段的發電量較少而不受到運營商的重視。近年來，高風速風場開發飽和，低風速風場得到快速發展，風機的低風速發電性能得到了關注[4]。低風速風機對切入風速非常重視，因為其需要風機在盡量低的風速下正常啟動，保證正常切入，從而減少啟動故障。

風機設計決定了風機的切入性能。同時，風機的切入與運行環境密切相關。之前，人們對風機切入風速的研究較少，一般都取固定值。本文指出，風機切入風速與風場運行環境中的空氣密度密切相關。基于這一原理，結合不同季節空氣密度不同，提出了一種新的風機切入調節機制。這種模式只需修改控制邏輯算法（幾乎零成本投入），即可顯著提升發電量。

2 空氣密度調節的風機切入機制

空氣密度是指單位體積內空氣的質量。空氣密度越大，空氣中所攜帶的能量越多。風能捕獲模型[5]為：

[P=12ρACpλ，βv3] ? ? ? ? ? ? ? ? ? ? ? ?（1）

式（1）中，[P]為可捕獲功率;[ρ]為空氣密度;[A]為風機掃風面積;[Cp]為風機的風能利用系數，其是葉尖速比[λ]和槳距角[β]的函數;[v]為風速。

由式（1）可知，可捕獲功率[P]和空氣密度[ρ]成正比。在相同風速情況下，空氣密度越大的地方和季節，可捕獲功率越高。

風機切入風速的最佳設定是：風機從氣流中捕獲的能量，剛好滿足風機啟動并網條件。對于已經樹立的風機而言，掃風面積A和風能利用系數[Cp]等均為定值，則風機啟動與[Cp·ρv3]相關。在風速變化較小的情況下，可認為[Cp]不變，則風速啟動只與[ρv3]有關。對于空氣密度大的地區和季節，切入風速可以設置得稍微小一些。

假設風機在某空氣密度[ρ0]下風機設計切入風速為[v0]，則在某一時刻當地空氣密度[ρ1]下，根據式（2），切入風速[v1]可以設置為式（3）[6]。

[ρ0v30=ρ1v31] ? ? ? ? ? ? ? ? ? ? ? ? ? ? （2）

[v1=ρ0ρ13×v0] ? ? ? ? ? ? ? ? ? ? ? ? ? ? （3）

根據式（3），已知某一空氣密度下風機切入風速，即可計算實時的切入風速。

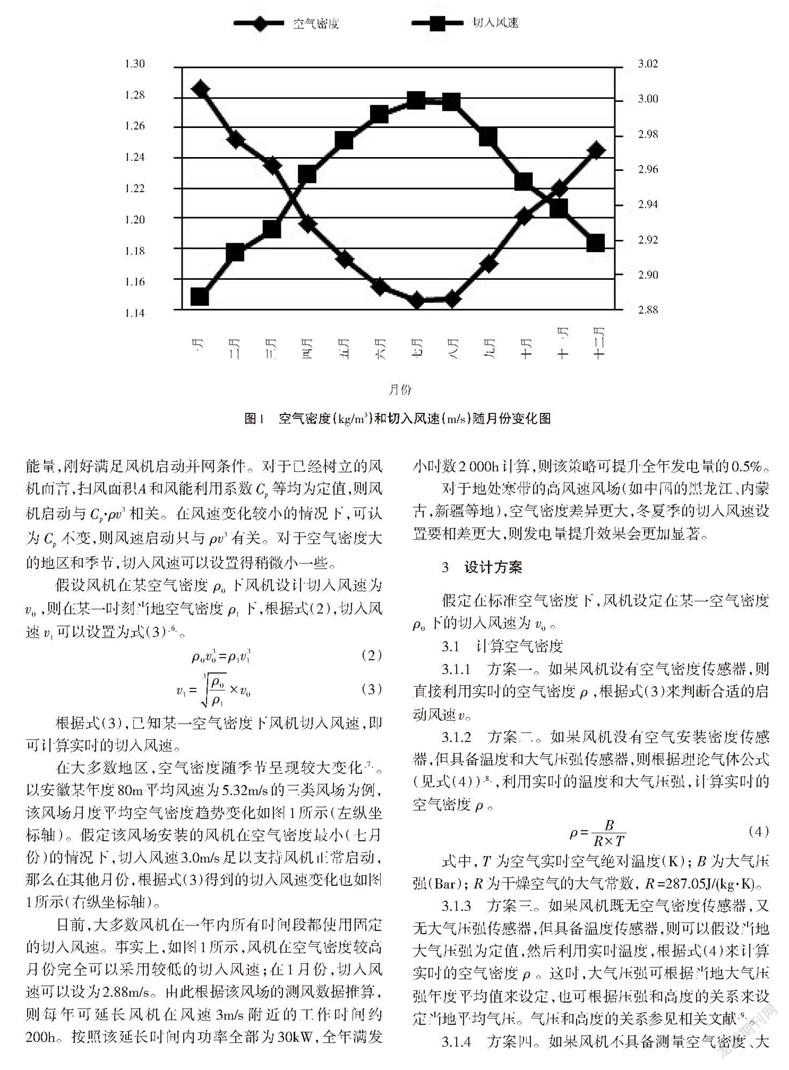
在大多數地區，空氣密度隨季節呈現較大變化[7]。以安徽某年度80m平均風速為5.32m/s的三類風場為例，該風場月度平均空氣密度趨勢變化如圖1所示（左縱坐標軸）。假定該風場安裝的風機在空氣密度最小（七月份）的情況下，切入風速3.0m/s足以支持風機正常啟動，那么在其他月份，根據式（3）得到的切入風速變化也如圖1所示（右縱坐標軸）。

目前，大多數風機在一年內所有時間段都使用固定的切入風速。事實上，如圖1所示，風機在空氣密度較高月份完全可以采用較低的切入風速;在1月份，切入風速可以設為2.88m/s。由此根據該風場的測風數據推算，則每年可延長風機在風速3m/s附近的工作時間約200h。按照該延長時間內功率全部為30kW，全年滿發小時數2 000h計算，則該策略可提升全年發電量的0.5%。

對于地處寒帶的高風速風場（如中國的黑龍江、內蒙古，新疆等地），空氣密度差異更大，冬夏季的切入風速設置要相差更大，則發電量提升效果會更加顯著。

3 設計方案

假定在標準空氣密度下，風機設定在某一空氣密度[ρ0]下的切入風速為[v0]。

3.1 計算空氣密度

3.1.1 方案一。如果風機設有空氣密度傳感器，則直接利用實時的空氣密度[ρ]，根據式（3）來判斷合適的啟動風速v。

3.1.2 方案二。如果風機沒有空氣安裝密度傳感器，但具備溫度和大氣壓強傳感器，則根據理論氣體公式（見式（4））[8]，利用實時的溫度和大氣壓強，計算實時的空氣密度[ρ]。

[ρ=BR×T] ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（4）

式中，[T]為空氣實時空氣絕對溫度（K）;[B]為大氣壓強（Bar）;[R]為干燥空氣的大氣常數，[R]=287.05J/（kg·K）。

3.1.3 方案三。如果風機既無空氣密度傳感器，又無大氣壓強傳感器，但具備溫度傳感器，則可以假設當地大氣壓強為定值，然后利用實時溫度，根據式（4）來計算實時的空氣密度[ρ]。這時，大氣壓強可根據當地大氣壓強年度平均值來設定，也可根據壓強和高度的關系來設定當地平均氣壓。氣壓和高度的關系參見相關文獻[9]。

3.1.4 方案四。如果風機不具備測量空氣密度、大氣壓強和溫度的所有設備，則可以根據當地年度空氣密度變化趨勢（可類似于二次曲線，如圖1所示），擬合出空氣密度變化規律，然后根據月份來對應插值得到近似的空氣密度，或者記錄每月空氣密度數值進行調用。由于這種近似可能存在較大誤差，所以設置參數時需要預留較大的閾值。

目前，大多數廠家風機具備外置溫度傳感器，所以第三種方案具有廣泛的適用性。

3.2 計算實時啟動風速

計算出實時的空氣密度[ρ]后，根據式（3）和給定空氣密度下的啟動風速[v0]，即可計算實時啟動風速[v0]。

4 結論和討論

本文利用風場空氣密度的變化特性，給出一種空氣密度調節風機切入的新模式，并給出了4種設計方案。該模式只需要修改控制算法而不需要任何其他硬件投入，即可實現發電量的有效提升。在一個平均風速為5.32m/s的低風速風場，增加這種機制將帶來0.5%的發電量提升。預期在空氣密度變化更為顯著的寒冷地帶，發電量提升將更加顯著。接下來，筆者將在寒冷地帶做測試，以證實這種機制對發電量提升的貢獻。

風機切入風速可能與多種因素有關，空氣密度只是其中一個易于控制且非常顯著的參數。進一步，筆者可以研究其他因素如湍流強度、入流角、天氣對切入風速的影響，以及風場環境對風機控制的影響，并進一步優化風機控制，達到提升發電量的目的。

參考文獻：

[1]李晶，方勇，宋家驊，等.變速恒頻雙饋風電機組分段分層控制策略的研究[J].電網技術，2005（9）：15-21.

[2]姚駿，廖勇，瞿興鴻，等.直驅永磁同步風力發電機的最佳風能跟蹤控制[J].電網技術，2008（10）：11-15.

[3]趙仁德，王永軍，張加勝.直驅式永磁同步風力發電系統最大功率跟蹤控制[J].中國電機工程學報，2009（27）：106-111.

[4]楊秀媛，梁貴書.風力發電的發展及其市場前景[J].電網技術，2003（7）：78-79.

[5] Tony Burton.風能技術[M].武鑫，譯.北京：科學出版社，2007.

[6]International Electrotechnical Committee. IEC 61400-1： Wind turbines part 1： Design requirements[S]. International Electrotechnical Commission，2005.

[7] CARTA，Antonio J，MENTADO，et al. A continuous bivariate model for wind power density and wind turbine energy output estimations[J]. Energy Conversion & Management， 2007（2）：420-432.

[8]汪志誠.熱力學與統計物理[M].北京：高等教育出版社，2008.

[9] Minzner R A. The 1976 Standard Atmosphere and its relationship to earlier standards[J]. Reviews of Geophysics，1977（3）：375-384.