形狀因子表征MCC顆粒形貌與粉體流動性的關系

李金寶 馬飛燕 修慧娟 趙欣 馮盼 楊雪

摘要：由于微品纖維素（ Microcrystalline cellulose，MCC）顆粒形貌不規整，難以定量表征，因此很難在顆粒形貌與粉體流動性之間建立定量關系。本研究嘗試用形狀因子（圓形度、伸長率、緊實度、同體性）對6種微品纖維素（MCC）顆粒的微觀形貌進行定量表征，探討了差異最顯著的形狀因子圓形度與其他形狀因子之間的相關性，并建立圓形度與MCC粉體流動性之間的數值關系。結果表明，流動件差異大的MCC顆粒形狀因子中圓形度差異最顯著;無論MCC粉體流動性如何，圓形度與其他形狀因子均存在一定程度的正負相關性;網形度分布越集中，流動性越好;圓形度與表征MCC粉體流動性的休止角之間符合一次線性關系。

關鍵詞：微品纖維素;微觀形貌;流動性;形狀因子

中圖分類號：TQ01;TS71

文獻標識碼：A DOI： 10. 11980/j. issn.0254-508X. 2019. 12. 001

微晶纖維素（Microcrystalline cellulose， MCC）作為一種重要的纖維素類功能材料，由于其獨特的理化性質被大量研究[1-2]，目前已廣泛應用于醫藥[3]、食品[4]、化工[5]等工業領域。粉體的流動性是MCC應用在各領域的關鍵性能指標之一，而MCC顆粒的微觀形貌對粉體流動性的影響至關重要[6-7]。由于顆粒復雜的微觀形貌難以定量表征，與流動性之間難以建立量化關系，一般只能定性地認為，顆粒粒徑越大，外形越接近球狀的粉體流動性越好[8-10]。

粒子幾何形態可通過對三維粒子在平面上的二維投影進行圖像分析，然后確定若干形狀因子來表達。粉體幾何形狀與其物理性能緊密相關，且表征顆粒幾何形貌的各形狀因子間存在一定相關性，已有許多研究學者在利用形狀因子表征顆粒微觀形貌方面做了大量有意義的工作[11-14]，但在各形狀因子間的相關性及其與粉體流動性的相關性方面鮮有研究。

本研究采用4個形狀因子（圓形度、伸長率、緊實度、固體性）量化表征6種MCC顆粒的復雜形貌，對比分析流動性差別較大的兩種MCC顆粒的形態特征差異，并探討差異最顯著的形狀因子——圓形度與其他各形狀因子間的相關性及圓形度與MCC粉體流動性之間的量化關系。

1實驗

1.1原料和試劑

原料為6種不同種類MCC（記為樣品A、B、C、D、E、F），其中樣品A、B、C取自日本旭化成株式會社;樣品D、E、F為不同原料或條件下實驗室自制MCC。6種MCC的性能指標如表1所示。

1.2圖像采集與分析

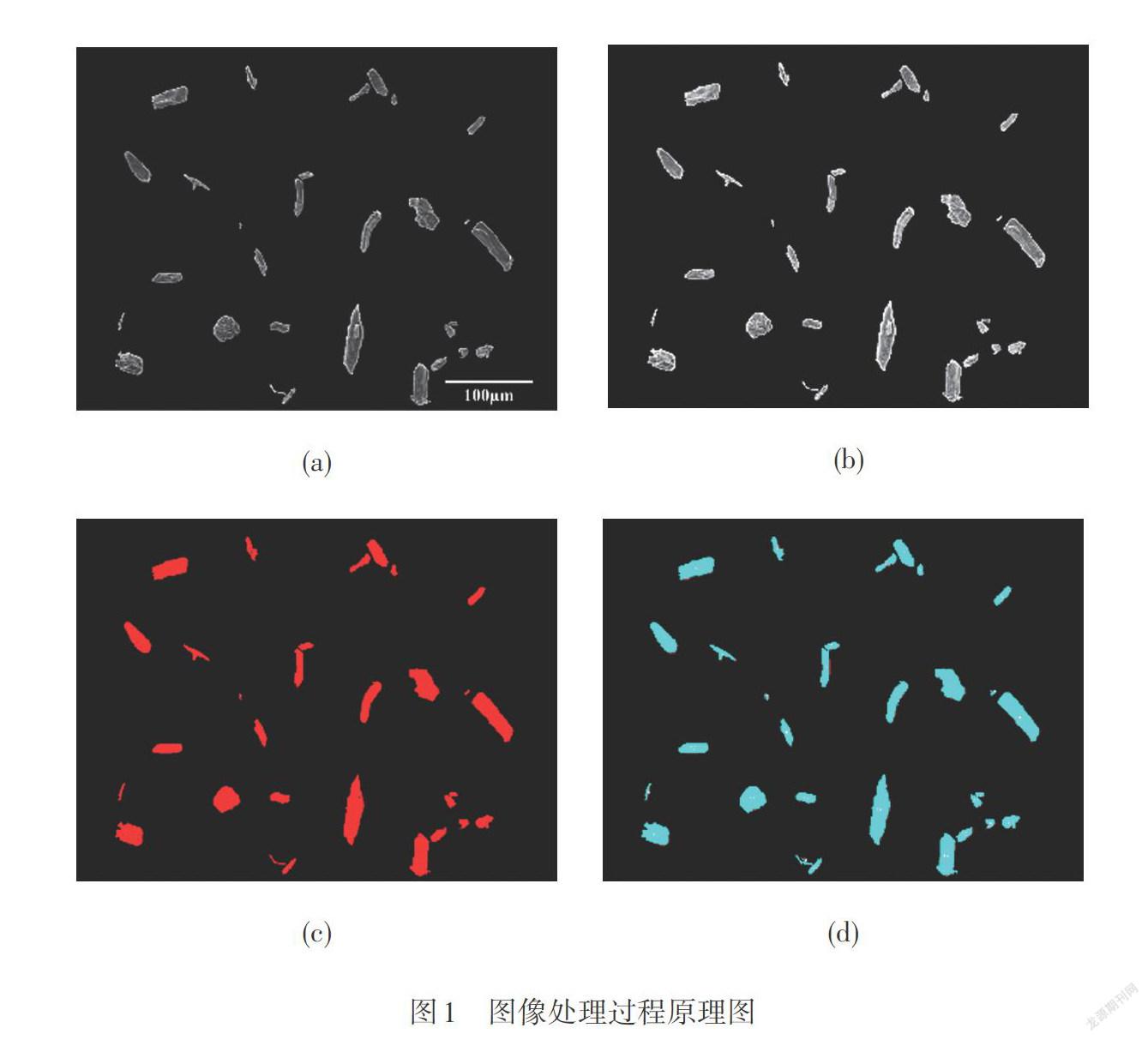
樣品經噴金處理后，采用FEI Q45型環境掃描電子顯微鏡（Thermo Fisher Scientific Inc.公司，美國）在500倍下獲取MCC顆粒形貌的SEM圖（見圖1（a））。然后采用Photoshop軟件對SEM圖進行圖像邊界平滑處理，得到邊界清晰的顆粒圖像輪廓線（見圖1（b））。每個試樣共隨機采集和處理1000個顆粒圖像。

利用Image J分析軟件進行數字圖像分析，首先設置8位圖像灰度值，然后通過調節閾值來精準地選取顆粒，直到閾值化后的圖像（二值圖像）呈高亮顯示為止（見圖1（c））。最后對圖像中顆粒進行統計（見圖1（d）），通過軟件自帶函數計算獲得數字圖像中每個顆粒的輪廓周長、投影面積，以及圓形度、伸長率、緊實度、固體性等形狀因子數據。

1.3形狀因子計算

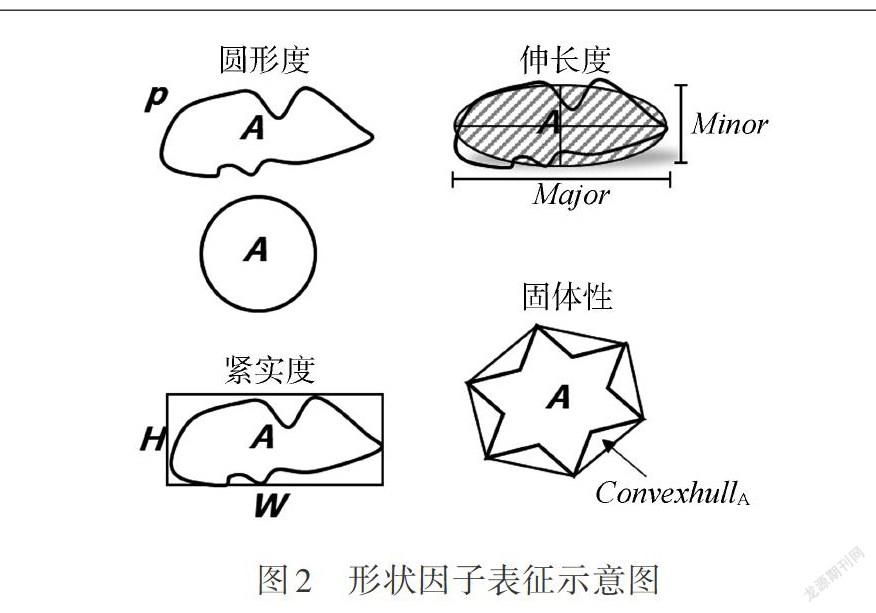
采用圓形度、伸長率、緊實度和固體性共4個形狀因子對顆粒形狀進行表征，圖2為4個形狀因子的表征示意圖，其中A為不規則顆粒的投影面積，P為不規則顆粒的輪廓周長，H為不規則顆粒外切矩形的高度，W為不規則顆粒外切矩形的寬度，具體計算公式見式（1）～式（4）。

圓形度=4πA P2 （1）

式中，A為不規則顆粒的投影面積;P為不規則顆粒的輪廓周長。

伸長率=1-MainorA/MajorA

（2）式中，MajorA為不規則顆粒最佳擬合橢圓的主軸長;MinorA為不規則顆粒最佳擬合橢圓的次軸長。

緊實度=A/W·H

（3）式中，A為不規則顆粒的投影面積;W為不規則顆粒外切矩形的寬度;H為不規則顆粒外切矩形的高度。

固體性=A ConvexhullA

（4）式中，A為不規則顆粒的投影面積;ConvexhullA。為不規則顆粒的包絡曲線內的面積。

1.4粉體流動性表征

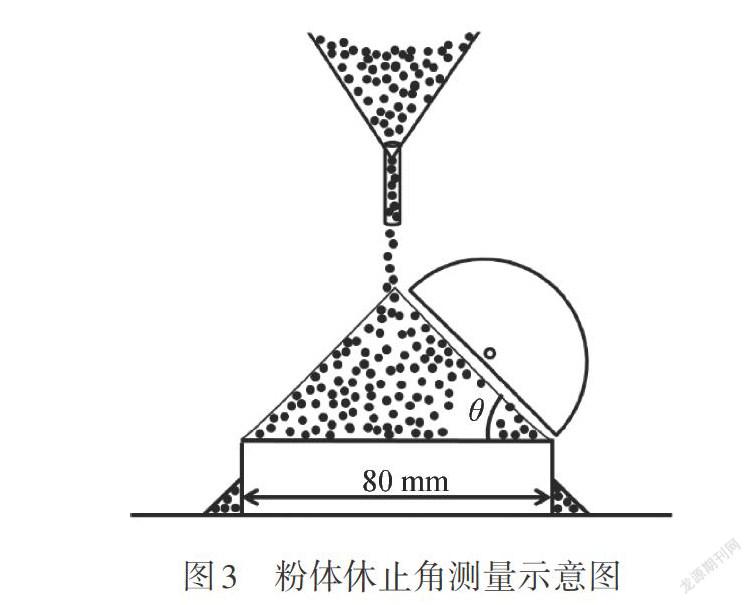
MCC粉體的流動性用休止角法[15]進行表征，利用BT-1OOO型粉體綜合特性測試儀（丹東百特儀器有限公司，中國）通過注入法[16]測定MCC粉體的休止角，測量示意圖如圖3所示。 2結果與討論 2.1不同MCC顆粒形貌特征差異的統計分析

MCC顆粒的微觀幾何形貌對流動性的影響至關重要，因此，本實驗對不同流動性的MCC顆粒形貌特征進行差異性分析。由于樣品數據量大，不能一一體現，從表1中可以看到，樣品A和樣品D的休止角分別為46.9°和56.2°，說明粉體流動性差異較大，因此，筆者選取樣品A和樣品D作為研究對象，使用統計分析軟件SPSS 21.0采用箱型圖[17]量化分析各個形狀因子值的分布狀態及大小，從而分析顆粒的形態特征差異。

箱型圖是一種顯示一組數據分散情況的統計圖，不僅可以反映數據分布的特征，還可以對多組數據分布特征進行比較。圖4為箱型圖的示意圖，箱型圖分析中用到統計學的四分位數（Quartile）的概念，所謂四分位數，就是把組中所有數據由小到大排列并分成4等份，處于3個分割點位置的數字分別就是第一四分位數（Q1）、第二四分位數（Q2）、第三四分位數（Q3），其中Q2為中位數，Q1與Q3的差距稱四分位間距。

樣品A和D的形狀因子箱型圖對比如圖5所示。箱體相對于縱坐標的高度能夠表現出顆粒各形狀因子的整體大小，箱體本身長度即整個四分位間距能夠表現出形狀因子的集中程度，結合樣品A和D的箱型圖統計量（見表2）對比樣品A和樣品D形態發現，流動性較高的樣品A顆粒的圓形度和緊實度與樣品D顆粒相比整體偏高，伸長率恰好相反，且樣品A和D顆粒的固體性整體稍高，差別不大。對比樣品A和D顆粒的各個形狀因子的四分位間距，樣品A顆粒圓形度、伸長率和緊實度的四分位間距分別為0. 231、0. 302和0.166，均小于樣品D顆粒的，說明樣品A網形度分布更加集中，顆粒形狀更加規則。而樣品A和D顆粒固體性的四分位間距相差不大，分散程度接近。分析可得，圓形度、緊實度及固體性整體偏高，且四分位間距均較小即形狀因子分布較集中的粉體流動性較好。

綜合對比樣品A和樣品D兩種流動性區別明顯的MCC顆粒的形態特征，4個形狀因子中圓形度整體大小以及分散程度差異最顯著，伸長率次之，緊實度和固體性差異都較小，因此圓形度是4個形狀因子中表征顆粒形態特征差異最顯著的參數，探究其與其他形狀因子之間的關系以及建立其與流動性之間規律可在一定程度上有助于量化表征MCC顆粒形貌與粉體流動性的關系。

2.2MCC顆粒圓形度與其他形狀因子關系的分析

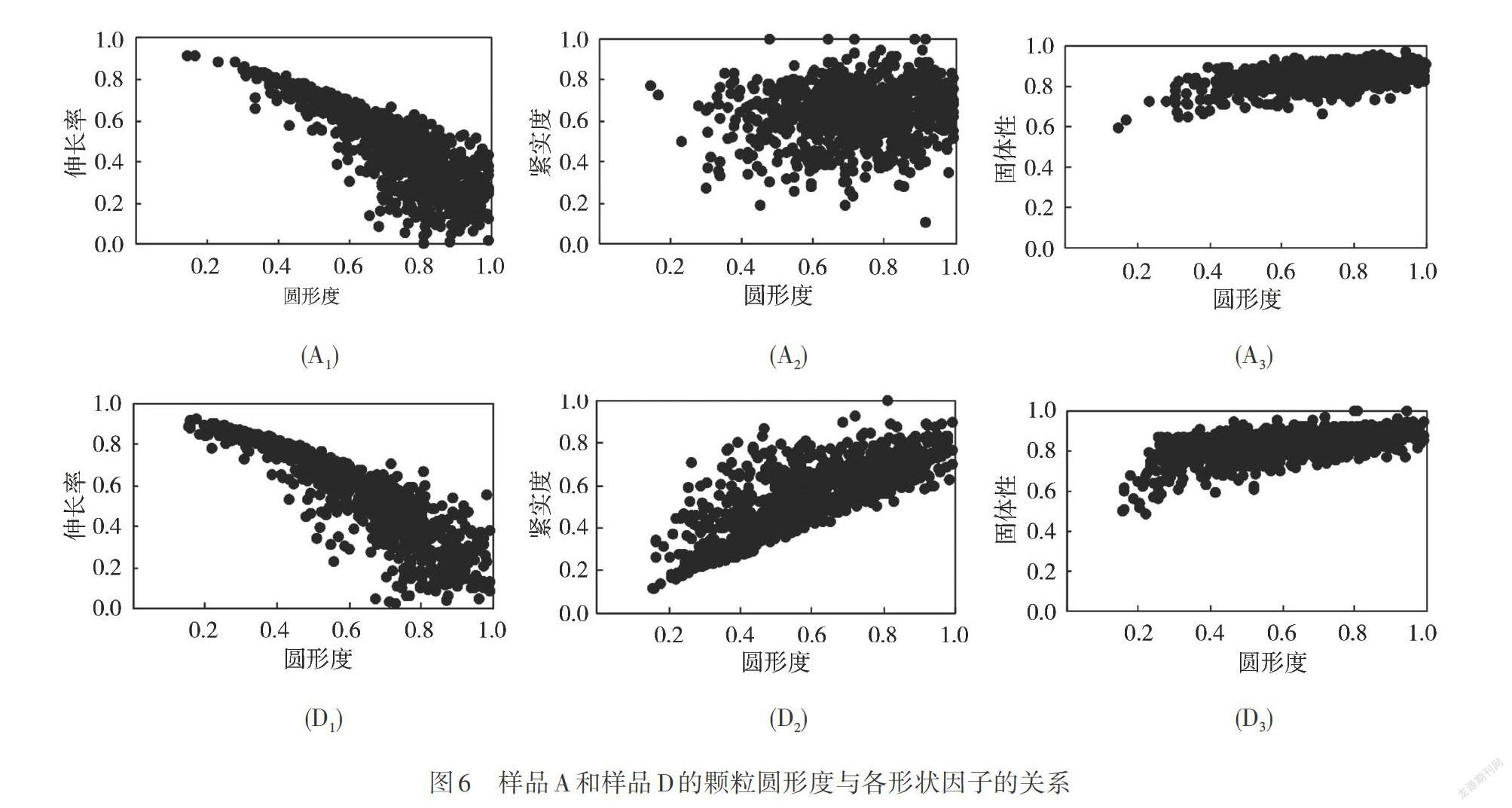
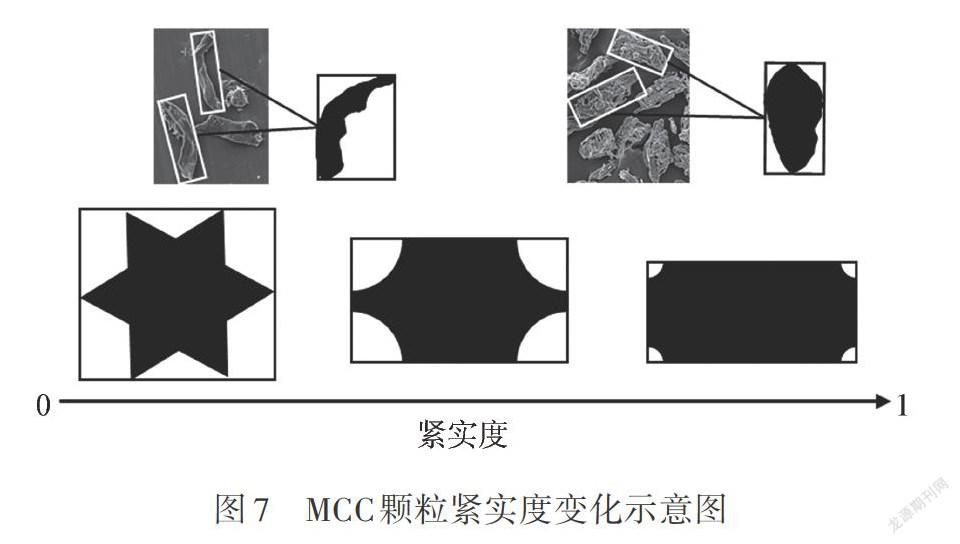
圓形度是顆粒最為基本且表征顆粒形態特征差異最顯著的形狀因子指標，與其他形狀因子可能存在一定相關性。繼續以流動性差別較大的樣品A和樣品D為研究對象，對圓形度與其他各形狀因子之間的關系進行分析。圖6中，A1、A2、A3圖分別為樣品A的顆粒圓形度與其他3個形狀因子的關系圖，D1、D2、D3圖分別為樣品D的圓形度與其他3個形狀因子的關系圖。圖中實驗值由大量的點顯示，通過觀察發現顆粒圓形度與其他3個形狀因子間存在變量關系。從關系圖A1與D1中可以看到，隨著MCC顆粒圓形度的增加，樣品A和D的伸長率均逐漸降低，呈反比例變化趨勢;A2與D2關系圖分別顯示樣品D的緊實度相對于圓形度的增大略有上升，呈正比例變化關系，而樣品A的緊實度隨圓形度增大變化趨勢不明顯，且緊實度普遍偏大，出現這一現象原因可能是由于圓形度較大的顆粒形態更穩定，不易變形，圓形度較小的顆粒形態更偏細長，易產生彎曲，導致顆粒本身投影面積占外切矩形的比例減小，即緊實度降低（見圖7）;A3與D3兩個關系圖顯示樣品A和D的固體性隨著圓形度的增加均略有上升，呈正比例變化趨勢，即隨著圓形度增大，顆粒凸度越大，圓形的凸度值為1。MCC顆粒圓形度與伸長率、緊實度、固體性的關系表明，不規則顆粒各形狀因子不獨立存在，具有一定相關性。

2.3MCC顆粒圓形度與粉體流動性的關系

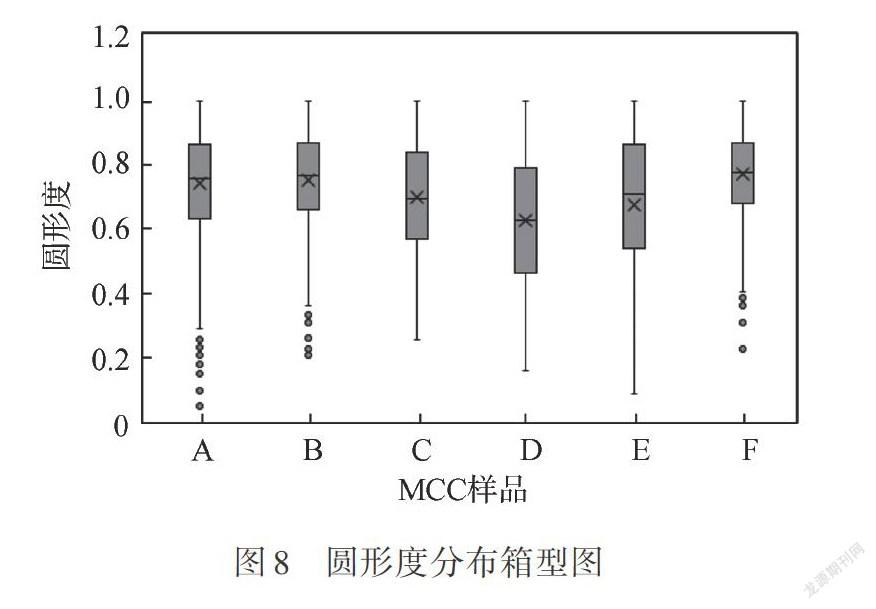
經上述研究可知，圓形度是表征顆粒形態較為重要的形狀因子，與其他形狀因子間有一定的相關性，更與粉體流動性有著密切關系，建立其與流動性之間規律有助于量化表征MCC顆粒形貌與粉體流動性的關系。為了探究圓形度與流動性之間的相關性，首先探究顆粒圓形度分布狀態與流動性之間的關系，將6種MCC顆粒的圓形度分布狀態及相關數值結合流動性采用箱型圖（見圖8）和表3來直觀比較。

箱型圖箱體相對于縱坐標的高度能夠表現出顆粒圓形度的整體大小，對比6種MCC，樣品F的箱體高度相對最高，即圓形度整體偏高，樣品D的箱體高度相對最小，即網形度整體偏小。6種MCC樣品的網形度整體大小排序為：F>B>A>E>C>D。箱體長度即整個四分位間距代表圓形度集中50%（即75%～25%）的數據，能夠表現出圓形度的集中程度，圓形度越集中，即MCC顆粒形狀越規則，結合圖8及表3對比6種MCC樣品，樣品F的圓形度四分位間距為0.188，圓形度分布最集中，相應的顆粒形狀也最規則，樣品D的圓形度四分位間距為0. 331，圓形度分布最分散，即顆粒形狀最不規整。6種MCC樣品的圓形度集中程度排序為：F>B>A>C>E>D。對比發現，MCC顆粒的圓形度整體越大，其圓形度分布也會越集中，顆粒更加規則，從而粉體的流動性更好。

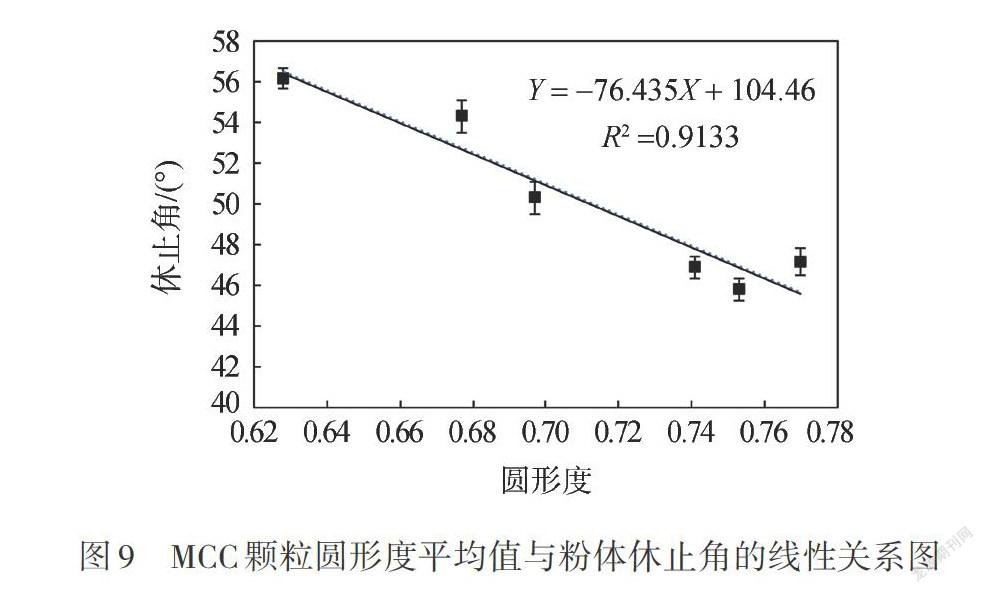
在分析MCC顆粒圓形度分布與粉體流動性之間關系的基礎上定量研究圓形度與粉體流動性之間的相關性，對6種不同MCC顆粒的圓形度平均值和其宏觀粉體休止角（見表3）進行數值擬合，擬合結果如圖9所示。

由圖9可以看出，不同種類MCC的圓形度平均值與粉體休止角之間符合一次線性關系，擬合的可決系數R2值為0.9133，擬合程度較高。因此，可以在一定程度上用圓形度平均值來量化表征MCC顆粒形狀對其粉體流動性的影響，他們二者之間大致存在的函數關系為式（5）。

Y=-76.435X+104.46

（5）

式中，y為MCC粉體的休止角;X為MCC顆粒的圓形度平均值。

即隨著圓形度平均值增大，粉體的休止角減小，流動性變好。原因是當圓形度越大時，MCC顆粒的二維形貌越接近圓形，三維形貌越接近球形，從而使得粉體流動時顆粒間的接觸面積、作用力較小，粉體的流動性越好。

3結論

本研究采用形狀因子（圓形度、伸長率、緊實度、固體性）對6種微晶纖維素（MCC）顆粒的微觀形貌進行定量表征，對比不同MCC顆粒的形貌特征差異，探討差異最顯著的形狀因子與其他形狀因子之間的相關性，并建立其與MCC粉體流動性之間的數值關系。

3.1流動性區別較大的兩類MCC，其顆粒形狀因子中圓形度的差異最顯著。

3.2MCC顆粒圓形度與其他形狀因子存在一定的正負比例相關性。

3.3當MCC顆粒的圓形度分布越集中，則顆粒越規則，粉體流動性越好。

3.4MCC顆粒的圓形度與粉體的休止角存在線性函數關系，函數關系式為Y=-76.435X+104.46，顆粒的圓形度越大時，粉體的流動性越好。

參 考 文 獻

[1]ZHANG Xiangrong， ZHANG Meiyun， Ll Jinhao， et al High Value-added Utilization of Cellulose： Mirocrystalline Cellulose Preparation[J]. China Pulp&Paper， 2014， 33（5）： 24張向榮，張美云，李金寶，等.纖維素高值化利用制備微品纖維素[J].中國造紙，2014， 33（5）：24.

[2]HAN Ying， L1 Fengping， FAN Tingting， et al. Study on Reed MCCPreparation Process by Acid Hydrolysis [J]. China Pulp& Paper，2015， 34（1）：71.韓穎，李鳳萍，樊婷婷，等酸法制備蘆葦微品纖維素工藝的研究[J].中國造紙，2015， 34（1）：71.

[3] CHU Ming， LIU Yanchen， ZHAINC Mingbo， et al.Study on Prepa-ration of Berberine Hydrochloride Sustained-release Tablets [J].Progress in Modern Biomedicine， 2016， 16（23）：4415初明，劉彥辰，張明波，等.鹽酸小檗堿緩釋片的研制[J].現代生物醫學進展，2016， 16（23）：4415.

[4]JIANG Xuhang， L1 Xiaoxuan， WANG Ren， et al.Impact of micro-crystalline cellulose on the quality and texture of bread[J].Scienceand Technology of Food Industry， 2013， 34（3）：90姜旭邦，李曉瑄，王韌，等.微品纖維素對面包品質和全質構的影響[J].食品工業科技，2013， 34（3）：90.

[5] LI Hua， YUAN Chunlong， SHEN Jie. Application of Superfine GrindingTechnology in Process of Grape Seeds [J]. Journal of South ChinaUniversity of Technology（ Natural Science Edition）， 2007（4）： 123.李華，袁春龍，沈潔.超微粉碎技術在葡萄籽加工中的應用[J].華南理工大學學報（自然科學版），2007（4）：123.

[6] ZHANGMeiyun， WANG Jing， Ll Jinhao， et al.Effect of Ball Mill-ing on Morphology， Structure and Properties of Microcrystalline Cel-lulose[J]China Pulp& Paper， 2018， 37（4）：7.張美云，王靜，李金寶，等.球磨對微品纖維素形態結構與性能的影響[J]中國造紙，2018， 37（4）：7.

[7]WU Fuyu.Study on flow properties of powders and characterization techniques[D].Shanghai：East China University of Science and Technology，2014.吳福玉.粉體流動特性及其表征方法研究[D].上海：華東理工大學，2014.

[8]Goh HP，Heng PWS，Liew CV.Comparative evaluation of powder flow parameters with referenee to particle size and shape[J].International Journal of Pharuaceuties，2018，547（1/2）：133.

[9]Mihranyan A，Stromme M.Fractal aspects of powder flow and densification[J].Particle and Particle Systems Characterization，2007，24（3）：223.

[10]WANG Shiho.ZHANG Lei，ZHANG Changli，et al.Characteriza-tion of polyethylene powder flowability and its factor analysis[J]China Synthetie Resin and Plastics，2013，30（6）：48.王世波，張磊，張長禮。等.聚乙烯粉料流動性的表征及影響因素分析[J].合成樹脂及塑料，2013，30（6）：48.

[11]Saad M，Sadoudi A.Rondel E，et al.Morphological characterization of wheat powders，how to characterize the shape of particles[J].Jourmal of Foond Engineering，201l，102（4）：293.

[12]AImeida-Pricto S，Blanco-Mendez J，Otero-Espinar FJ.Microscopic image analysis techniques for the morphological characterization of phamaceutical particles：Influence of the software，and the factor algorithms used in the shape factor estimation[J].European Joumal of Pharmaeeuties and Biopharmaceuties，2007，67（3）：766.

[13]Wiwat M，Suchowilska E，Lajszner W，et al.ldentification of hybrids of spelt and wheat and their parental forms using shape and color deseriptors[J].Computers and Eleetroaics in Agriculture.2012，83：68.

[14]Grulke E A，Yamamoto K，Kumagai K，et al.Size and shape distributions of primary crystallites in titania aggregates[J].Advanced Powder Technology，2017，28（7）：1647.

[15]HAN Peng，CHEN Fang-cheng，TU Jia-sheng.Flowability evalua-tion of silicified microerystalline cellulose[J].Journal of China Pharmaceutical University，2013，44（5）：416.韓鵬，陳方城，涂家生.硅化微晶纖維素粉體流動性評價[J].中國藥科大學學報，2013，44（5）：416.

[16]SUN Huinan，CHEN Xu，XIA Chaoyong.Measurement and Exper-iment Study on Angle of Repose of Paddy[J].Modern Food，2018（2）：63.孫慧男，陳旭，夏朝勇.稻谷休止角的測定與實驗研究[J].現代食品，2018（2）：63.

[17]Li D C，Huang WT，Chen C，et al.Employing box plots to build high-dimensional manufacturing models for new products in TFT-LCD plants[J].Neurocomputing，2014，142：73.CPP

（責任編輯：常青）