考慮多工況和病態(tài)載荷的穩(wěn)健結構拓撲優(yōu)化設計

陳一雄 趙圣佞 陳成 石軍

摘 要：多工況載荷下，結構拓撲優(yōu)化中的病態(tài)載荷問題仍是一個開放的課題。因此，結合變體積約束限技術，構建新的近似拓撲優(yōu)化模型，提出了一種解決結構柔順度拓撲優(yōu)化中病態(tài)載荷問題的優(yōu)化方法。首先，構建多種載荷工況下結構柔順度的雙重凝聚函數(shù)，形成新的連續(xù)體拓撲優(yōu)化模型。其次，基于有理分數(shù)材料懲罰模型和移動漸近線表示式，形成目標函數(shù)和約束函數(shù)的顯式二次近似式。最后，利用光滑化對偶算法，給出具有收斂性的多工況載荷下連續(xù)體結構的柔順度拓撲優(yōu)化算法。給出的算例結果表明，與現(xiàn)有方法相比，該方法能解決多工況載荷下結構拓撲優(yōu)化中的病態(tài)載荷問題，且可獲得更優(yōu)和清晰0/1分布的結構拓撲。

關鍵詞：可行域調(diào)整;柔順度優(yōu)化;結構拓撲優(yōu)化;多載荷工況

中圖分類號：TG156 文獻標識碼：A 文章編號：1003-5168（2019）01-0037-04

Robust Topology Optimization Design of Structures Considering

Multiple Load Cases and Ill-loaded Problem

CHEN Yixiong1，2 ZHAO Shengning1，2 CHEN Cheng1，2 SHI Jun1，2

（1.School of Automotive and Mechanical Engineering，Changsha University of Science and Technology，Changsha Hunan? 410114;2.Key Laboratory of? Lightweight and Reliability Technology for Engineering Vehicle，College of Hunan Province，Changsha Hunan 410114）

Abstract： The ill-load problem of structural compliance topology optimization under multiple load cases still was an opening topic of the structural topology optimization field. Combining with a varied volume limit scheme， a novel approximate model of structural compliance topology optimization under multiple load cases was constructed， and a newmethod called as a duplicate aggregation function method was proposed， which was adopted to solve the ill-load problem of structural compliance topology optimization under multiple load cases. At first， a duplicate aggregation function for structural compliances under multiple load cases was constructed， and a novel approximate topology optimization model was formed. Based on the rational approximation for material properties （RAMP） and the Method of Moving Asymptotes（MMA）， explicitconvex and separable quadratic approximate functions of objective and constraint functions were derived. Then， a compliance topology optimization approach for multiple load cases， possessing convergence， was proposedby adopting a smooth dual algorithm. It was concluded from given examples that the proposed method can solve the ill-load problem of structural compliance topology optimization under multiple load cases， and may obtain a more optimal topology with clear 0/1 distribution than the existed methods.

Keywords： feasible domain adjustment;compliance optimization;structural topology optimization;multiple load cases;ill-loaded cases

在現(xiàn)代工程結構中，常見的一些重要產(chǎn)品結構在復雜載荷工況條件下工作，且載荷工況之間的載荷量級相差很大，甚至在同一載荷工況內(nèi)，不同結構部位間的載荷量級也存在很大差異。例如，主要的承載機械結構可能需要留有安裝傳感器的部位或者一些工作平臺等，故機械結構除了工作強載荷作用外，還在偏離強載荷作用部位的某處存在小載荷作用。如果小載荷或小載荷工況存在，或者小載荷作用的部位不處于強載荷的傳力路徑上，那么在基于傳統(tǒng)優(yōu)化方法的多工況載荷下的結構拓撲優(yōu)化過程中，可能會出現(xiàn)沒有材料支承小載荷的優(yōu)化結構，即所謂的病態(tài)載荷。為了解決病態(tài)載荷問題，隋允康等根據(jù)載荷的量級將載荷分成兩個層次[1]，即分別考慮強載荷和弱載荷進行結構拓撲優(yōu)化設計，最終結果取決于兩個層次的劃分，且不同載荷的量級差異并不能完全反映它們導致的結構柔順度的量值差異。James等提出一種結構柔順度的[η2]范數(shù)凝聚方案[η2>1]解決多工況載荷下結構柔順度拓撲優(yōu)化問題[2]。Luo也利用結構柔順度的[η2]范數(shù)研究了多剛度優(yōu)化設計問題[3]。基于不同工況載荷作用的結構柔順度的量值差異特征，Cai等人考慮從0.1～0.5中取一個小值[η1][4]，形成結構柔順度的[η1]范數(shù)凝聚函數(shù)，以解決兩組載荷工況下的病態(tài)載荷問題。Shi和Cai將該小值[η1]范數(shù)的凝聚方案擴展到雙模材料的病態(tài)載荷工況的結構拓撲優(yōu)化中[5]。該方法的仿真結果顯示，當結構受到超過兩組工況載荷作用且這些工況載荷含有病態(tài)載荷以及其中的兩組大載荷工況的結構柔順度值相近時，基于小值[η1]范數(shù)凝聚方案的結構柔順度拓撲優(yōu)化求解只能獲得一個較差的局部解。對于僅有兩組工況載荷的情況，該方法甚至能解決拓撲優(yōu)化的病態(tài)載荷問題，但難于獲得最優(yōu)解。本文針對含有病態(tài)載荷的多工況載荷環(huán)境下結構柔順度拓撲優(yōu)化問題，提出一種新的優(yōu)化方法，以解決結構柔順度拓撲優(yōu)化的病態(tài)載荷問題，獲得較好的結構拓撲優(yōu)化解。

1 含有病態(tài)載荷的多工況載荷下結構拓撲優(yōu)化模型

對于指定體積約束的多工況載荷下結構柔順度優(yōu)化問題，實質(zhì)要求是使[maxl=1，2，…，LClρ]最小。

針對含有病態(tài)載荷的多工況載荷環(huán)境下結構柔順度拓撲優(yōu)化問題，本文構建式（1）的結構柔順度的雙重凝聚函數(shù)[faggρ]，并將它作為多工況載荷環(huán)境下結構柔順度拓撲優(yōu)化模型的近似目標函數(shù)。

[faggρ=l=1LClρClmρ0η1η2η1+l=1LClρClmρ0η11η2]（1）

式中，L表示載荷工況總數(shù)，[Cl]表示第l組工況載荷作用下的結構柔順度，[lm]為最大初始結構柔順度值[Clmρ0]對應的載荷工況序號，[η1]和[η2]為經(jīng)驗參數(shù)，分別取小于1和大于1的值。因此，本文基于最大結構柔順度最小和預定結構體積要求，構建了多工況載荷環(huán)境下結構柔順度拓撲優(yōu)化模型：

[minfaggρ=l=1LClρClmρ0η1η2η1+l=1LClρClmρ0η21η2s.t.? ?q=1QρavnqV0nq+p=1pραvipV0iq/V0≤V*/V0Kρulρ=Fl，l=1，2，…，Lρminnq≤ρnq≤1，q=1，2，…，Q]（2）

式中，[V*]表示約束的體積值，[V0]為初始結構的體積值，而K表示結構總剛度陣。[Fl]為第l組工況載荷，[ul]為第l組載荷工況下結構的位移響應。取[ρminnq=10-5]，以避免結構總剛度陣奇異。

2 結構柔順度的靈敏度分析和多工況載荷下結構拓撲優(yōu)化近似模型

引入如式（3）、式（4）所示的變體積限技術：

[Vk+1u=Vk-minβ1V0，V*-Vk，Vk≥V*Vk+minβ1V0，V*-Vk，Vk<V*? ?，k=1，2，3]（3）

[Vk+1U=maxVkU-β1V0，V*，V4≥V*minVkU+β1V0，V*，V4<V*? ?，k=4，5，…]（4）

式中，[β1]為經(jīng)驗參數(shù)，取值范圍為[0.005，0.025];[Vk]表示第k迭代步的結構體積;[λk]是前一步（第k步）的拉格朗日乘子。

式（4）中，[Vk+1U]相對于迭代步k是單調(diào)變化的。在進行有限迭代步后，式（2）的可行域完全與優(yōu)化模型（4）的可行域一致。式（2）的收斂性完全由求解算法確定。另外，變體積約束限技術的引入使得近似優(yōu)化模型（2）易于用對偶方法求解，且基于措施的優(yōu)化方法可獲得序列清晰拓撲。

再者，類似于文獻[6，7]，將人工變量[w1]引入到模型（2），至此得到拓撲構型可穩(wěn)健變化的優(yōu)化模型（5）。

[minfk0ρ+c1w1+12d1w21s.t.? ?fk1ρ-w1≤0ρ∈ρk，w1≥0]? ? ? ? ? ? ? ? ? （5）

3 算例

圖1左端固定的懸臂梁尺寸為2m×1m×0.002m，其彈性模量和泊松比分別為200GPa和0.3。作用于結構的三組工況載荷都為集中載荷工況。工況載荷一的集中載荷[F1]為8 000N，沿鉛垂方向向下作用于結構的右端中點。工況載荷二的集中載荷[F2]為10N，沿鉛垂方向向下作用于結構的右端上端點。工況載荷三的集中載荷[F3]為10 000N，沿鉛垂方向向下作用于結構的上邊中點。將初始設計域劃分為等尺寸的5 000個平面應力單元，并指定目標體積比[θ=0.4]。本文取長度過濾尺寸為[rmin=3.0Δmin]（[Δmin]是結構單元邊長的最小尺寸）。初始設計結構的拓撲變量都為1.0。收斂參數(shù)取為[ε1=0.000 1]和[ε2=0.000 1]。雙重凝聚函數(shù)的兩個參數(shù)[η1]和[η2]分別取0.2和10。

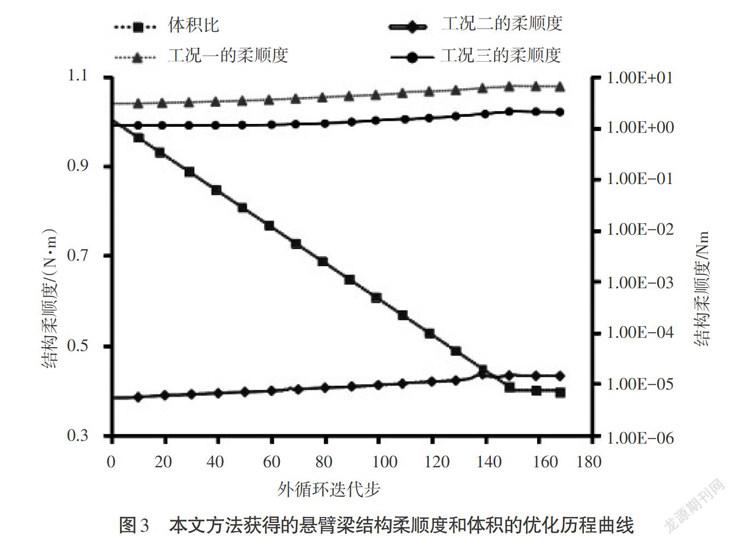
圖2為本文方法獲得的懸臂梁結構拓撲優(yōu)化歷程圖。可以看出，盡管載荷的量級相差非常大，在最后的構型中仍然有材料支撐弱載荷，可獲得較好的拓撲優(yōu)化解。這充分說明本文方法是有效的，能夠解決病態(tài)載荷問題。圖3給出了本文方法獲得的懸臂梁結構的結構體積比和各工況載荷下結構的柔順度的優(yōu)化歷程曲線。不難看出，整個優(yōu)化歷程是穩(wěn)健變化的。

4 結論

本文提出了解決病態(tài)載荷問題的一種新的多工況載荷下連續(xù)體結構的柔順度拓撲優(yōu)化求解方法。從方法的理論公式和給出的算例可以得出以下結論：①提出的結構柔順度拓撲優(yōu)化方法能解決病態(tài)載荷問題，且具有收斂性和好的穩(wěn)健性;②本文方法可獲得更優(yōu)、更清晰0/1分布的優(yōu)化結構拓撲。

參考文獻：

[1]隋允康，彭細榮，葉紅玲.ICM應力全局化方法克服連續(xù)體拓撲優(yōu)化的載荷病態(tài)[J].工程力學，2009（6）：1-9.

[2]James K A，Hansen，Jorn S，et al.Structural Topology Optimization for Multiple Load Cases Using a Dynamic Aggregation Technique[J].Engineering Optimization，2009（12）：1103-1118.

[3]Luo Z，Chen L P，Zhang Y Q，et al.Multi-stiffness Topological Optimization for Continuum Structures with Multiple Loading Cases and a Duplicate Sensitivity Filtering Method[J].Acta Mech Solida Sin.，2005（1）：29-36.

[4]Cai K，Shi J，Zhang A.Stiffness Design of a Continuum Under Ill-load Cases by Fractionalnorm Objective Formulation[J].Optimization and Engineering，2014（4）：927-944.

[5]Cai K，Cao J，Shi J，et al.Optimal Layout of Multiple Bi-modulus Materials[J].Struct. Multidisc. Optim.，2016（53）：801-811.

[6]Groenwold A A，Etman L F P，Wood D W.Approximated Approximations for SAO[J].Structural and Multidisciplinary Optimization，2010（1）：39-56.

[7]Etman L F P，Groenwold A A，Rooda J E. irst-order Sequential Convex Programming Using Approximate Diagonal QP Subproblems[J].Structural and Multidisciplinary Optimization，2012（4）：479-488.