對兩條生活經驗的理性探索
楊亞軍


摘 要:數學源于生活,但由于數學的高度抽象,讓學生對數學心存恐懼.數學建模作為數學核心素養,在學生的眼中往往高不可攀.筆者結合教材中的一道例題,結和學生平時提過的一個問題,以探索兩條生活經驗背后的科學依據,讓學生體會、感受如何把實際問題數學化,利用數學工具去解決,以此來消除學生對數學建模的恐懼感,也讓學生感受那些貌似冰冷、古怪的數學公式、數學結論骨子里的熱情與魅力,激發學生對數學學習的興趣.
關鍵詞:數學建模;數學應用;數學的魅力
生活中,人們積累了許多行之有效的經驗,往往能快捷、有效地解決有關問題.下面,咱們通過兩個具體的例子,一起來體會探索生活經驗背后的科學依據.
經驗1:人們要把一段圓形木料截成長方形,要使截出來的長方形木料面積最大,只需按該圓的內接正方形截即可.這經驗的科學依據是什么?能用我們所學的數學知識給出解釋嗎?
下面我們用圓代替圓形木料,上述經驗可表述為:圓的內接矩形中,正方形的面積最大.以下探索這種說法的科學依據.
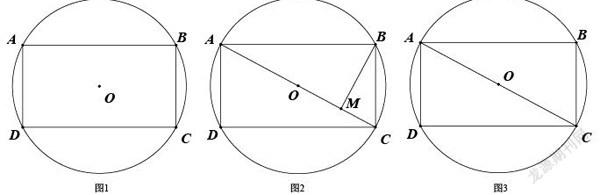
如圖1,設矩形ABCD是的內接矩形,的半徑為(定值).以下探索:當矩形ABCD是正方形時其面積最大.
如圖2,連結AC,過點B作AC的垂線,垂足為點M,則,顯然點B到AC距離的最大值為R,此時點M與點O重合,亦即AB=BC時,矩形ABCD的面積最大.這就是這條生活經驗背后的數學依據.
若是注意到圓和它的內接矩形都是軸對稱圖形,且他們有共同的對稱軸,比如圖4中的直線EF就是它們的一條公共對稱軸.我們亦可把問題轉化為:在半圓中研究矩形ABEF面積取最大值的條件.
經驗2:為了推進某條公路沿線各村經濟的的發展,政府擬在該公路沿線的某處建設一個農產品交易市場.若只考慮沿線各村從村口的公路到該市場的路程總合最小,該市場位置應建在何處?生活經驗告訴我們,該市場應建在這段公路旁所有村子里最靠近“中間”的村子附近.這經驗的科學依據是什么?能用我們所學的數學知識給出解釋嗎?
下面我們用直線代替該條公路,把這個問題放在數軸上研究.如圖5,我們用各村口該公路的里程數表示該村在數軸上的相對位置,設這n個村子村口該公路的里程數分別為,設交易市場所在位置該公路的里程數為x.
通過對這兩條生活經驗的探究,讓我們對這些生活經驗有了更深刻、理性的認識.更為重要的是:讓我們真切地體會到了數學的工具性和數學的應用價值.與此同時,也體驗了如何恰當地引入變量,用數學的符號語言、用數學模型把實際問題理想化、簡單化成一個數學問題,再用數學的有關知識、方法、結論等解決該數學問題,進而解決對應的實際問題.在這樣的實踐探索中,曾經的那些抽象、古怪的數學公式、數學結論、數學方法變成了一個個具體、有生命力的解決問題的工具.具體到下面這些數學結論:(2α),(當且僅當時等號成立),(當且僅當時等號成立),它們在我們研究上述問題時是不是很給力?我們現在對它們的認識和感覺是不是也不一樣了?!
參考文獻
[1]《數學必修4》,嚴士健,王尚志主編,北京師范大學出版社,2017.7(2018.12):125.
[2]張中華,淺議數學核心素養中數學模型能力的培養,《上海中學數學》,2018(11):3-5.
(作者單位:陜西省寶雞中學)

