人口統(tǒng)計(jì)數(shù)據(jù)系統(tǒng)誤差探析
陳海俠
摘要:一定年齡尾數(shù)數(shù)據(jù)的觀測(cè)值與真值相比存在的偏離就稱作人口統(tǒng)計(jì)數(shù)據(jù)系統(tǒng)誤差。此文針對(duì)以往人口統(tǒng)計(jì)的檢驗(yàn)方式展開分析研究,并指出其中的缺陷,且提出新型檢驗(yàn)手段,使用其對(duì)廣義人口函數(shù)的年齡變動(dòng)系統(tǒng)誤差進(jìn)行檢測(cè),能夠判斷傳統(tǒng)檢驗(yàn)手段無法判斷的存在散失以及年齡積聚之類的數(shù)據(jù)信息,此種方法與以往檢驗(yàn)手段相比是有較大優(yōu)勢(shì)的。
關(guān)鍵詞:人口統(tǒng)計(jì);數(shù)據(jù)檢測(cè);系統(tǒng)誤差分析
數(shù)據(jù)屬于人口統(tǒng)計(jì)中非常關(guān)鍵的條件因素。因此,保障其質(zhì)量是非常重要的。必須針對(duì)數(shù)據(jù)質(zhì)量以及誤差進(jìn)行明確認(rèn)識(shí)的基礎(chǔ)上,才可以從數(shù)據(jù)當(dāng)中獲得最準(zhǔn)確結(jié)論。人口數(shù)據(jù)一般都是統(tǒng)計(jì)得到的,所以難免會(huì)有誤差存在,通常能夠分成系統(tǒng)誤差、過失誤差以及隨機(jī)誤差。此文主要對(duì)系統(tǒng)誤差進(jìn)行分析。
一、空間信息與人口信息
人口信息主要指的是和人相關(guān)的人口質(zhì)量、數(shù)據(jù)和人口結(jié)構(gòu)之類的數(shù)據(jù)信息。空間信息指的是將地球表層現(xiàn)象借助數(shù)學(xué)抽象用符號(hào)化語言來表達(dá)處理。人口數(shù)據(jù)具備顯著的時(shí)空特征,必須將人口信息和地理空間信息有效結(jié)合起來,若是行政區(qū)域出現(xiàn)改變,才可以精準(zhǔn)反映在變化之后該區(qū)域人口信息。這樣,同一地區(qū)不同時(shí)間人口數(shù)據(jù)具有可比性,最終才可以把人口數(shù)據(jù)和其余社會(huì)經(jīng)濟(jì)要素的統(tǒng)計(jì)數(shù)據(jù)展開綜合性研究。人口統(tǒng)計(jì)信息一定要添加空間分布信息才可以稱作和現(xiàn)代經(jīng)濟(jì)以及社會(huì)發(fā)展水平適應(yīng)的人口信息。且空間信息能夠在相關(guān)邊界區(qū)域內(nèi)提升任意數(shù)量屬性數(shù)據(jù),比如:人口性別年齡的分布,文化組成,民族組成,職業(yè)組成,行業(yè)組成,婚姻情況以及流動(dòng)人口情況之類內(nèi)容,進(jìn)而對(duì)不同特點(diǎn)的人口分布與變化進(jìn)行靈活制約,使得政府決策,地區(qū)規(guī)劃,城市管理以及企業(yè)市場(chǎng)分析能夠有據(jù)可依。
二、人口數(shù)據(jù)空間方法介紹
人口統(tǒng)計(jì)數(shù)據(jù)和空間特性相互連接,依照研究問題需求,其連接具有全局以及局部性方案。其中全局方案就是將該趨于視為“均質(zhì)”性地區(qū),而如此一來人口統(tǒng)計(jì)數(shù)據(jù)就可以表示為此區(qū)域平均值。局部方案就是在各個(gè)“均質(zhì)”區(qū)域人口內(nèi)部分布都不斷變化,這便表明,我們必須依照統(tǒng)計(jì)數(shù)據(jù)針對(duì)人口實(shí)際的分布狀況展開模擬又或是近似表現(xiàn)出來。全部的這些都必須做好人口統(tǒng)計(jì)數(shù)據(jù)空間分析。統(tǒng)計(jì)數(shù)據(jù)的空間化本質(zhì)在于依據(jù)地理空間信息數(shù)據(jù)結(jié)構(gòu)實(shí)現(xiàn)統(tǒng)計(jì)數(shù)據(jù)再組合以及有效化管理,屬于完成多種統(tǒng)計(jì)數(shù)據(jù)和地理空間數(shù)據(jù)的匹配,從而針對(duì)附著到區(qū)域上的相關(guān)統(tǒng)計(jì)數(shù)據(jù)怎樣變化展開模擬的一個(gè)過程。
三、人口數(shù)據(jù)系統(tǒng)年齡錯(cuò)誤研究
數(shù)據(jù)系統(tǒng)誤差特征在于觀測(cè)值一直朝著同一方向進(jìn)行偏差,其誤差大小以及符號(hào)進(jìn)行重復(fù)觀測(cè)時(shí)大體一致。人口年齡數(shù)據(jù)系統(tǒng)誤差具體表現(xiàn)為特定年齡上(比如:一個(gè)偶數(shù),0和5是其尾數(shù))人口函數(shù)觀測(cè)值超過或者低于其實(shí)際值。這種誤差是廣泛存在所有以年齡作為自變量人口函數(shù)之中的。
人口統(tǒng)計(jì)學(xué)通常借助人口年齡統(tǒng)計(jì)數(shù)據(jù)質(zhì)量評(píng)估手段,此文稱作指數(shù)方式,一般依靠邁耶爾指數(shù),惠普爾指數(shù)以及聯(lián)合國(guó)的綜合指數(shù)。此種指數(shù)法是先要建設(shè)起年齡有均勻變化的一個(gè)人口,將其作為標(biāo)準(zhǔn),針對(duì)研究對(duì)象人口以及標(biāo)準(zhǔn)人口的年齡結(jié)構(gòu)展開對(duì)比,將兩者的離差視作具體的尺度,對(duì)人口年齡數(shù)據(jù)的精準(zhǔn)性進(jìn)行判斷,針對(duì)質(zhì)量較低數(shù)據(jù)來指出什么年齡尾數(shù)人口存在集聚又或是散失。邁耶爾指數(shù)法以及惠普爾指數(shù)法僅適合對(duì)人口年齡結(jié)構(gòu)進(jìn)行檢驗(yàn),對(duì)于廣義人口年齡數(shù)據(jù)適不適合的。而聯(lián)合國(guó)綜合指數(shù)是通過整體對(duì)人口的年齡性別變化的平穩(wěn)性進(jìn)行判斷,然而無法對(duì)某尾數(shù)年齡堆積進(jìn)行判斷,因此在這里是不進(jìn)行討論的。為了使得人口年齡數(shù)據(jù)系統(tǒng)誤差具有直觀印象。具體針對(duì)某省份女性年齡結(jié)構(gòu)展開分析。
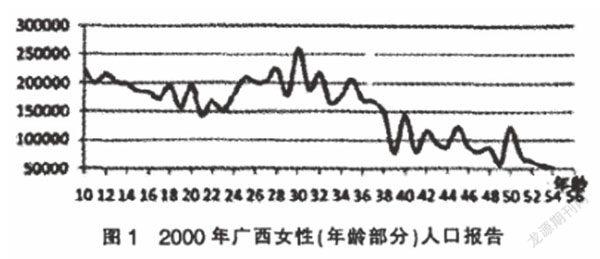
①女性的人口年齡結(jié)構(gòu)(見圖1)
對(duì)圖1進(jìn)行觀察能夠清楚了解到,0、5、8結(jié)尾年齡,其人口要顯著多于其左右的年齡人口。對(duì)于出現(xiàn)于人口集聚在一些特定尾數(shù)年齡的情況我們就稱作人口堆積。
現(xiàn)時(shí)人口年齡結(jié)構(gòu),屬于歷史人口自然變動(dòng)還有社會(huì)變動(dòng)共同導(dǎo)致。如果在歷史上人口變動(dòng)不屬于周期性變化,那么年齡人口數(shù)便不會(huì)每間隔5個(gè)年齡以及10個(gè)年齡存在一個(gè)高峰期。
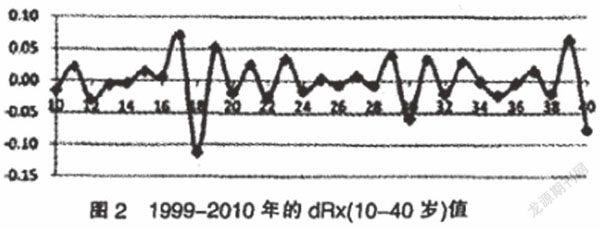
②1999~2010的人口存活率(見圖2)
我們?cè)倭私飧鶕?jù)兩次普查人口進(jìn)行的存活率誤差計(jì)算。
圖2為1999~2010年的兩次人口普查dRx數(shù)值,我們?yōu)榉奖阌^察的更加明確,所以上圖僅對(duì)部分的年齡段進(jìn)行選取。若是兩次人口普查人口年齡數(shù)據(jù)保證準(zhǔn)確的話,那么存活率就是NRx。并且屬于均勻變化。dRx數(shù)值應(yīng)當(dāng)是依據(jù)一定方向進(jìn)行穩(wěn)定變化,就算人口普查與抽樣調(diào)查人口年齡數(shù)據(jù)存在誤差,若是隨機(jī)性的,不存在年齡尾數(shù)指向,則dRx數(shù)值同樣應(yīng)當(dāng)隨機(jī)波動(dòng)。然而對(duì)上圖記性觀察能夠了解到,dRx數(shù)值變化是不穩(wěn)定的,屬于上下波動(dòng)的,而且此類波動(dòng)并不隨機(jī),存在顯著規(guī)律性:如果x為奇數(shù),dRx>0,如果x為偶數(shù),dRx<0。另外一種說法是:如果x為奇數(shù),NRx>0.5(NRx-1+NRx+1),如果x為偶數(shù),NRx<0.5(NRx-1+NRx+1),因此屬于系統(tǒng)誤差。
以上情況表明,從1999~2010的兩次普查數(shù)據(jù)中得到存活率觀測(cè)數(shù)值,奇數(shù)年齡的時(shí)候要高于存活率實(shí)際值,偶數(shù)年齡要低于存活率實(shí)際值。出現(xiàn)此種狀況,能夠設(shè)想在兩次人口調(diào)查之中最少一次調(diào)查中的一些年齡尾數(shù)存在人口的集聚以及散失問題,其中可能會(huì)兩次調(diào)查之中都有人口集聚或者散失,還可能僅為其中的一次,若是僅其中的一次調(diào)查存在質(zhì)量問題,則還應(yīng)當(dāng)了解上一次的調(diào)查質(zhì)量或者是之后調(diào)查質(zhì)量。
因?yàn)槿丝跀?shù)據(jù)的改變程度存在差異,有關(guān)人口的年齡曲線形狀以及方向影響是不同的。通常而言,人口數(shù)據(jù)出現(xiàn)變化的時(shí)候(在某一年齡存在積聚或者散失),首先改變其形狀,再改變其方向,因此,進(jìn)行實(shí)際的數(shù)據(jù)檢驗(yàn)之時(shí),會(huì)出現(xiàn)誤判問題,為了避免出現(xiàn)誤判問題,我們還應(yīng)當(dāng)思考人口數(shù)據(jù)的性質(zhì)又或是與其余數(shù)據(jù)結(jié)合進(jìn)行思考。
四、人口函數(shù)年齡變化的符號(hào)分布檢驗(yàn)
此文提出了對(duì)人口系統(tǒng)誤差進(jìn)行判斷的一種新手段,此手段適合廣義人口函數(shù)年齡變化系統(tǒng)誤差的判斷,我們稱作為符號(hào)分布檢驗(yàn)法。在這里廣義的人口主要包含遷移、生育、婚姻以及死亡之類。對(duì)于將年齡視作自變量的人口、死亡以及生育之類函數(shù)全都稱為人口函數(shù)。
人口函數(shù)的年齡變化符號(hào),假使年齡是自變量x,而人口屬于年齡函數(shù),具體用Y(x)進(jìn)行表示(x取0,1,2,…),而Y(x+1)-Y(x)就屬于Y(x)于x中的一階差分。設(shè)DYx=Y(x)-(Y(x-1)+Y(x+l))/2用其對(duì)x年齡人口和兩邊年齡人口平均值之間差值進(jìn)行表示。如果Yx>0,就說明Y扭)數(shù)值在x中呈現(xiàn)增長(zhǎng)趨勢(shì),這時(shí)曲線提升。如果x=0,就說明Y(x)于x時(shí)數(shù)值超過兩邊年齡的平均值,函數(shù)曲線屬于凸?fàn)睿绻鸇YxS的時(shí)候,以上假定是否定的,相反以上的假定就是肯定。如果假設(shè)肯定,就判定異常屬于隨機(jī)出現(xiàn),對(duì)象人口數(shù)據(jù)并不具備特定年齡尾數(shù)指向。如果假定是否定的,就判定因?yàn)閳?bào)告特定年齡尾數(shù)指向而導(dǎo)致。
五、結(jié)束語
此文方式必須一定基礎(chǔ),假使人口年齡曲線的變化形狀與方向特征符號(hào)于各年齡之中屬于隨機(jī)分布,如果假設(shè)是肯定的,數(shù)據(jù)不具備特定年齡尾數(shù)指向,相反就判定具備尾數(shù)指向。作者進(jìn)行過相關(guān)驗(yàn)證,只要采取以往的指數(shù)法能夠判斷出的積聚與散失人口數(shù)據(jù),應(yīng)用此文手段也是可以判斷出來的。而采取以往的指數(shù)法判斷不出來的,采取此文提到方式能夠判斷出來,所以表明此方法與以往方法相比更加有效。因?yàn)榇宋姆椒ū仨毟怕逝袛嘧鳛榛A(chǔ),進(jìn)行實(shí)際數(shù)據(jù)檢驗(yàn)的時(shí)候,會(huì)有出現(xiàn)誤判的可能性,為了防止誤判現(xiàn)象,還應(yīng)當(dāng)考慮到人口數(shù)據(jù)性質(zhì)以及與其余的數(shù)據(jù)結(jié)合進(jìn)行考慮。
參考文獻(xiàn):
[1]黃容慶,曾學(xué)偉,王建志.人口分析技術(shù)方法[J].北京經(jīng)濟(jì)學(xué)院出版社,2014,17-28.
[2]喬肖淳,孫曉龍.淺析年齡結(jié)構(gòu)檢驗(yàn)指數(shù)應(yīng)用到中國(guó)的局限性[J].人口數(shù)據(jù)分析方法及其應(yīng)用.中國(guó)外文出版社,2014,13-27.
[3]翟真吳,姜振興,劉曉涵.常用的人口統(tǒng)計(jì)公式介紹[J].中國(guó)人口出版社,2014,28-32.

