《平行線性質綜合應用》教學案例

王世晶

本節課的主要內容是平行線性質的綜合應用，既是對上一節課平行線性質的鞏固提升，也是加深對性質的理解和應用。初一學生都具有好奇、好問的探究心理，創設問題情境，能夠迅速激發學生的興奮點，并且使學生把知識的學習當作一種自我需求。

本節課教師作為一個引路人，通過一個圖形進行多種變式設問，引發學生心理上的認識沖突，然后把探究的機會交給學生，充分調動學生的學習積極性、培養他們的創新意識、體現新課程理念下的交流與合作。

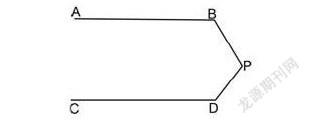
片段一：課前預習題：如下圖，已知AB∥CD，猜想∠BPD與∠B、∠D的關系，說明理由。

要求同學以小組為單位課前討論，盡可能給出不同的解法，上課時每組投影展示并講解比賽。比賽規則是：解法和解答問題正確次數多為獲勝組。因為要比賽，同學們的積極性都比較高，課前都做了充分準備。

上課一開始，同學們就進行了你爭我趕的展示、講解，氣氛非常活躍，教師即時就各組的解答進行點評，每一小組都猜想正確 ，但方法不一，共有以下5種解法。

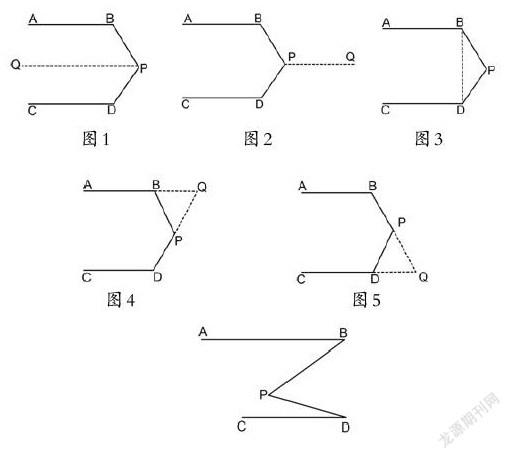
解法1：過P向左邊作平行線PQ，利用“兩直線平行，同旁內角互補”性質可得（如圖1）。

解法2：過P向右邊作平行線PQ，利用“兩直線平行，內錯角相等”性質和“周角定義”可得（如圖2）。

解法3：連接BD，利用“兩直線平行，同旁內角互補”性質和“三角形內角和”可得（如圖3）。

解法4：延長DP交AB的延長線于Q點，利用“兩直線平行，同旁內角互補”性質和“三角形內角和”以及“平角定義”可得（如圖4）。

解法5：與解法4類同，延長BP交CD的延長線于Q點（如圖5）。

片段二：例題：如下圖，已知AB∥CD，猜想∠BPD與∠B、∠D的關系，說明理由。

要求同學仿照預習題的方法盡可能給出多種解答，由于時間關系，要求以搶答形式，且每組只能搶不同的方法。

氣氛再次高漲，答案一個接一個地寫在黑板上，幾乎是標準答案。

片段三：教師乘勝追擊提出了新問題，請同學們比較課前預習題與例題，它們只是圖形發生了改變，條件和問題都相同。

仔細觀察這兩個圖形的結構特征，能否再次改變圖形，編制新題。課堂一下子沉靜了，教師抓住時機引導學生觀察這兩個圖形：它們無非是兩條平行線與三個角，把∠P看成可以上下、左右運動，把兩條平行線看成可以左右平移，那么圖形將如何畫出？請各小組馬上開始討論并展示。

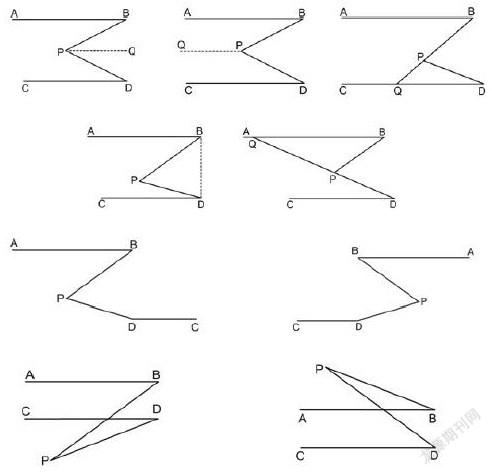
不一會兒，各組爭先恐后地繪出以下各圖。

教師、同學們都滿意地笑了，那么如何解答呢？時間已經不允許了，本題作為今天的作業。

教學后記：學生的學習過程既是一個認知的過程，又是一個探究的過程。在教學中，通過對一個圖形巧妙變式地創設問題，使學生在疑中生奇、疑中生趣，不斷激發學生的學習欲望和主動探究的意識，引導學生以小組為單位進行合作探究，可以創設和諧、寬松的課堂氛圍，讓每位同學都不脫離隊伍，讓每位同學都真正參與活動，強化了學生的主體意識，培養了學生的合作精神，也體現了團結、友愛、互幫互助的集體氛圍。

學習終究是學生的事，學習的效果取決于學生是否愉快地融入集體中，是否真正參與探究活動中，是否積極主動地思考;教師只是一個組織者和引導者，教師的責任更多是為學生提供合作的平臺，為學生創設思考的機會，為學生留有思考的時間;正如新課程理念所倡導的“尊重學生的需要，關注學習過程”。

本節課教師通過探究平行線性質的綜合應用，放手讓學生合作、猜想、探究、類比、歸納，使不同層次的學生都得到應有的收獲。

（責任編輯 ?周子瑩）