基于貝葉斯網絡的鋁型材擠壓過程異常檢測

楊 慧 芳

(廣東工業大學計算機學院 廣東 廣州 510006)

0 引 言

我國鋁型材產業是高能耗產業，鋁擠壓工藝平均能耗約為1 571～5 405 kg標煤每噸[1],是歐洲的1.43倍。而且近幾年的發展十分迅速，有數據顯示，截止至2015年我國鋁加工型材總量已達到26 000 kt/a，居世界第一，另鋁合金擠壓材產量也達到14 000 kt/a[2]。擠壓機作為鋁型材生產過程中的核心設備，發展日趨大型化、復雜化及自動化，在生產過程中一旦發生異常或故障，將會造成極大的停產損失，耗費大量的維護費用，甚至造成嚴重的安全事故。設備故障檢測方面的研究，一直是國內外學者關注的重點。賀惠新[3]對燃氣輪機故障模式的點形式及序列形式的異常行為的檢測方式進行了深入研究；周珂儀[4]研究了復雜結構系統長時間運行產生的一維以及多維時間序列的異常檢測方法；Soner Emec等[5]提出了一種用于制造設備的故障監控框架，以解決面對復雜情況下不可擴展的問題。標桿法[6]和人工免疫算法[7]在設備故障檢測方面也有不錯的效果。針對擠壓機的異常檢測問題近期也得到了廣大學者的關注，并有了研究成果。周理[8]針對大型擠壓機設備的多回路復雜液壓系統提出一種混雜鍵合圖與時間因果圖的故障診斷方法；江海昌[9]為解決檢測擠壓機點異常和模式異常的問題，分別提出了基于GA-SVR的擠壓機能耗點異常檢測模型和基于免疫算法的模式異常檢測模型；曾利云[10]研究了擠壓機能耗數據的特性，提出基于時間序列和聚類的異常檢測方法，通過改進的K-means算法和K-MDOF算法，在點異常和模式異常方面的檢測準確率有所提高。

現有針對擠壓機異常檢測的方法雖然有一定的效果，但面對傳感器故障或者歷史數據缺失嚴重等不確定性的情況，實驗效果達不到預期，準確率較低，而且只能判斷異常是否發生，不能定位異常原因，不能滿足車間生產的實際需求。

貝葉斯網絡作為一種人工智能技術，是不確定知識表達和推理領域最有效的理論之一[11]，已經被運用到很多領域，特別是機械設備故障檢測和預測方面。國內外學者通過分析機械設備的參數信息或者生產過程中的歷史數據[12]為軌道電路[13]、飛機[14]、冷水機組[15]、電力系統[16]、空氣制動系統[17]等建立貝葉斯網絡異常診斷模型，并在實驗中取得了不錯的效果。

擠壓機設備為高能耗裝置，生產過程中能源消耗情況最能真實反映設備狀態。本文提出通過分析擠壓機運行過程中的能耗傳遞機制，建立能耗模型，得到影響擠壓機能耗的關鍵因素。并以此為依據構建貝葉斯網絡結構，不僅克服結構學習算法占用內存的問題[18]，也減去單純依靠專家知識構造網絡的弊端。利用歷史數據中的先驗知識獲得條件概率表，構造完成貝葉斯網絡，再利用貝葉斯網絡推理算法檢測擠壓過程中設備異常狀態并做原因分析。結果表明，本文方法構造的貝葉斯網絡可以有效地檢測擠壓擠異常情況、分析出引起異常的原因，并且大大提高了檢測效率。

1 擠壓機設備能流機制分析

擠壓是使裝入擠壓筒內的坯料，在擠壓筒一端擠壓軸的推力作用下，使金屬從擠壓筒某一端的模孔流出，從而獲得與擠壓模孔形狀、尺寸相同的產品的一種塑性[19]。擠壓原理如圖1所示。

液壓系統的能源裝置是液壓泵，液壓系統共有三次能量轉化：1) 電動機通電，電能被轉化為機械能；2) 通過聯軸裝置，驅動液壓泵運轉將機械能轉換為液壓能，輸出高壓油，液壓泵工作時由于泄露和摩擦力等因素會造成一定的能量損耗；3) 通過控制各種閥門改變擠壓油缸中液壓油的流量，從而進行擠壓工作。期間由于液壓油進入閥門，在閥芯處的過流面積迅速變小，形成壓差，造成能耗損失。鋁型材的成型質量主要與擠壓溫度和加油速度有關，但在幾十秒乃至幾分鐘的擠壓周期內，擠壓溫度不好控制，可以通過控制擠壓速度平穩變化來控制擠壓溫度。

液壓系統的每次擠壓過程使用的總功率可以表示為[20]：

Pw=Pci+ΔPfh+ΔPmh

(1)

式中：Pci表示擠壓油缸的輸入功率，ΔPfh表示液壓系統閥門組的損失能量，ΔPmh表示液壓泵的損失能量，可通過液壓泵輸入功率與輸出功率之差計算得到。液壓泵得到輸入功率用Pmi表示[20]：

Pmi=2·π·nv·Tn

(2)

式中：nv代表液壓泵泵軸的轉速，Tn代表液壓泵的輸入轉矩。

液壓泵的輸出功率用Pmo表示[20]：

Pmo=p·Qm

(3)

式中：p代表液壓泵的泵口壓力，Qm代表液壓泵的實際流量，用公式表示為[20]：

(4)

式中:Vm是液壓泵的移動速度，Dm是液壓泵的直徑。

液壓泵的能量損耗ΔPmh可以表示為：

ΔPmh=Pmi-Pmo=2·π·nv·Tn-p·Qm

(5)

液壓閥門組的能耗損失表示為[20]：

ΔPfh=n·Δpf·ΔQf

(6)

式中:n代表閥門個數，Δpf代表閥口壓差，ΔQf代表閥口流量。

擠壓油缸輸入功率用Pci表示：

Pci=F·V

(7)

式中:F表示擠壓桿受到的力，V表示擠壓桿移動的速度[20]。

(8)

(9)

Q=εQm

(10)

式中:A表示液壓缸的有效面積;ηm表示液壓缸的機械效率;ηv液壓缸的容積效率;D表示活塞直徑;d表示活塞桿直徑;Q表示輸入液壓缸的流量;pa表示主缸壓力；ε表示擠壓油缸的容積效率。

2 擠壓機異常檢測貝葉斯網絡模型

2.1 貝葉斯網絡結構構建

貝葉斯網絡又稱為貝葉斯置信網絡(Bayesian Belief Networks)、信念網[21]，是一種基于網絡結構的有向圖解描述,適用于表達和分析不確定和概率性事物,可從不完全或不確定的知識或信息中作出推理。構建一個完整的貝葉斯網絡主要需要完成兩個任務：結構學習和參數學習。通過結構學習得到貝葉斯網絡結構，通過參數學習得到節點的條件概率表。最后利用貝葉斯網絡推理方法得到需要查詢的變量的后驗概率并更新網絡的概率參數。

在構建貝葉斯網絡時，主要采用基于評估函數和搜索算法的結構學習方法和基于節點依賴關系的結構學習方法[16]。基于評估函數和搜索算法的結構學習的主要缺點是參數間因果關系的建立過程不夠明確，需要經過多次學習-評估的過程才能找到最優的貝葉斯網絡結構，最后的結果很大程度上是由評估算法的好壞決定。在貝葉斯網絡的結構學習的過程中，為提高模型的精準度而造成網絡模型的復雜度不斷變大，復雜度適合的網絡模型往往實驗結果的精準度不夠高。基于節點依賴關系的結構學習的主要缺點需要先計算節點間的條件獨立性，而對于本身決定因素較多的節點，因為需要計算節點間的條件概率得到依賴關系強弱，而產生大量的冗余工作，不僅工作量巨大，還會耗費很多的存儲空間。

為提高貝葉斯網絡構建的效率和優越性，本文將通過第1節得到的能耗公式來構造能耗異常檢測的貝葉斯網絡結構圖B(I,E)，I代表節點，E代表連接邊。構建貝葉斯網的節點如表1所示。

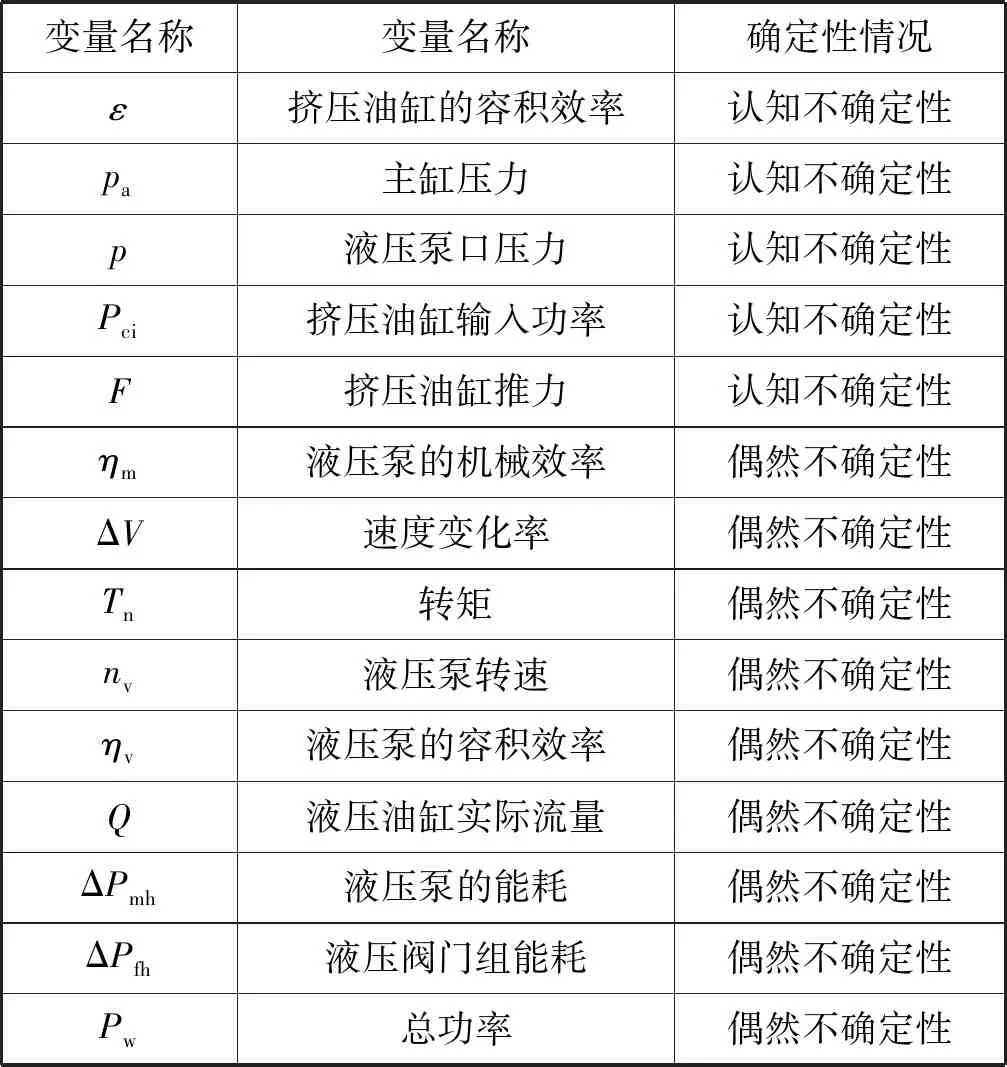
表1 節點表

通過分析能耗公式，得到節點間的相互依賴關系，以式(1)為例，可得Pw的值是ΔPmh、ΔPfh和Pci這三個節點取值之和，即Pw依賴于這三個節點，這三個節點為Pw節點的父節點。以此類推，構建的的網絡結構圖如圖2所示。

圖中認知不確定、分布未知的節點指節點概率分布未知；偶然不確定、分布已知的節點指節點概率分布已知，但存在偶然不確定性；有觀察值的節點指節點值可被人為觀測或有傳感器能采集數據。

2.2 節點的參數學習

貝葉斯網絡的參數學習[22]，即學習得到貝葉斯網絡節點的條件概率表。貝葉斯公式為：

(11)

式中:X1,X2,…,Xn是E的一個互不相容的完備事件組，且P(Xi)>0，Y是E的任意事件。

由式(11)可得要計算節點的條件概率，必須在之前計算得到先驗概率和聯合概率。步驟如下：

(1) 首先對節點進行預處理，根據歷史數據分析所有節點變量的取值集合。

(2) 處理證據變量，可通過分析歷史數據得到節點的概率分布情況，得到概率分布表。對于沒有觀測數據的節點，假設服從均勻分布，這也稱為貝葉斯假設。

(3) 對于非證據變量，要精確計算節點的條件概率幾乎不可能。因此，對于這些節點條件概率的學習，就是計算對于不同證據變量下節點條件概率的后驗分布。參數學習便轉換成貝葉斯網絡推理問題。

本文采用Gibbs抽樣算法[21]進行網絡的近似推理。假設抽樣m次，抽樣算法步驟如下：

(1) 首先根據要推理的結果，確定一個證據變量E=e，然后隨機生成與證據一致的樣本為起始樣本D1。

(2) 復制上一個樣本數據得到新的樣本數據，設定非證據變量的抽樣順序，根據抽樣順序，對非證據變量進行抽樣。

(3) 根據抽樣結果對當前樣本數據進行更新，若有k個非證據變量，則要依次抽樣k次，得到最終樣本。

(4) 重復進行步驟2-步驟3)，生成m個樣本，設m個樣本中，滿足查詢變量A=a(a為查詢變量的取值)的個數是n個，則可按下式近似計算查詢變量后驗概率。

(12)

2.3 貝葉斯網絡推理

貝葉斯網絡推理是指利用貝葉斯網絡的結構及其條件概率表，在給定證據變量后計算部分變量或者所有變量的邊緣概率或者最大概率狀態等問題。貝葉斯網絡的推理包括正向推理和逆向推理。正向推理是根據觀測到的節點的變化，修正貝葉斯網絡中其他節點的參數值，即在貝葉斯網絡推理過程中，網絡節點的信度參數會跟隨推理結果進行更新，通過貝葉斯網絡的自學習能力保證網絡的可信度；逆向推理是通過調整節點的參數，觀察其他節點參數的變化，從而分析得到各節點的狀態。貝葉斯網絡推理問題包括后驗概率問題、最大可能解釋問題(MPE)和最大后驗假設問題(MAP)。本文通過貝葉斯網絡模型要解決異常檢測與原因定位，即通過網絡推理解決后驗概率問題和最大可能解釋問題。計算在給定證據變量后，查詢變量異常狀態的概率。在判定設備異常情況下，計算節點在不同狀態下組合導致異常發生的概率，分析實際情況與更改狀態后概率值變化度，找出與實際情況下后驗概率的變化度最大的節點狀態組合，該狀態組合與實際情況下的差別狀態即是異常原因所在。

設R={Pa,ηm,ηv,nv,Tn,p,F,ΔV,Q,ΔPfh,ΔPmh,Pci,ε}，根據貝葉斯公式，判斷異常狀態的后驗概率公式如下：

P(Pw=0|R)=

(13)

根據鏈式規則:

P(X1X2…Xn)=P(X1)P(X2|X1)P(X3|X1,X2)…

P(Xn|X1X2…Xn-1)

(14)

將異常檢測網絡模型中的節點代入式(12),得到的聯合分布的公式如下：

P(R,Pw)=P(Pw|ΔPmh,ΔPfh,Pci)P(Pci|F,ΔV)P(Q|ε)

P(p)P(ΔPmh|nv,Tn,p)P(F|,pa,ηm)P(ΔV|Q,ηv)

P(ε)P(ηv)P(ΔPfh)P(pa)P(ηm)P(nv)P(Tn)

(15)

3 案例分析

本文以佛山某鋁型材企業擠壓車間SY-3600Ton型擠壓機為例，該車間每月生產鋁型材3 000噸，其中合格率在89%左右，經常由于不易察覺的異常出現導致鋁型材質量不合格，造成嚴重損失。本次實驗選擇了2018年2月-2018年3月的能耗數據庫中600個能耗數據樣本，并將其均勻分成3組，分別為A組、B組和C組。目前已知A組、B組和C組中的發生異常次數分別為15次、10次和12次，現對這些樣本數據進行能耗異常檢測。

為了評估本方法檢測異常的效果，現定義三個評估標準：一是誤檢率，即本方法檢測出現異常但實際并非異常情況的個數與總異常次數之比；二是漏檢率，即實際出現異常但本方法沒有檢測出來的異常次數與總異常次數之比；三是正確率，即本方法正確檢測到的異常次數與總異常次數之比。實驗操作步驟如下：

(1) 數據預處理：根據先驗知識和以往得到的歷史數據以及現場調研，得到在擠壓機運轉周期內，周期時間約為208 s,擠壓時間約為163 s，空機時間、空載前進時間、快速后退時間分別為12、20、12 s。不同狀態下擠壓力有所變化，因此對數據離散化后，節點有三個取值，1表示壓力為零,2表示空載前進或者快速后退階段(壓力在9～12 MPa)，3表示擠壓前進階段(壓力在16～20 MPa)。其余節點為兩個取值，其中1表示所采集的數據不處于正常范圍，2表示數值處于正常范圍區間。最后得到的節點數據統計表如表2所示。通過分析歷史數據得到觀測節點的概率分布和非觀測節點的假設先驗分布表，如表3和表4所示。

表2 節點數據統計結果

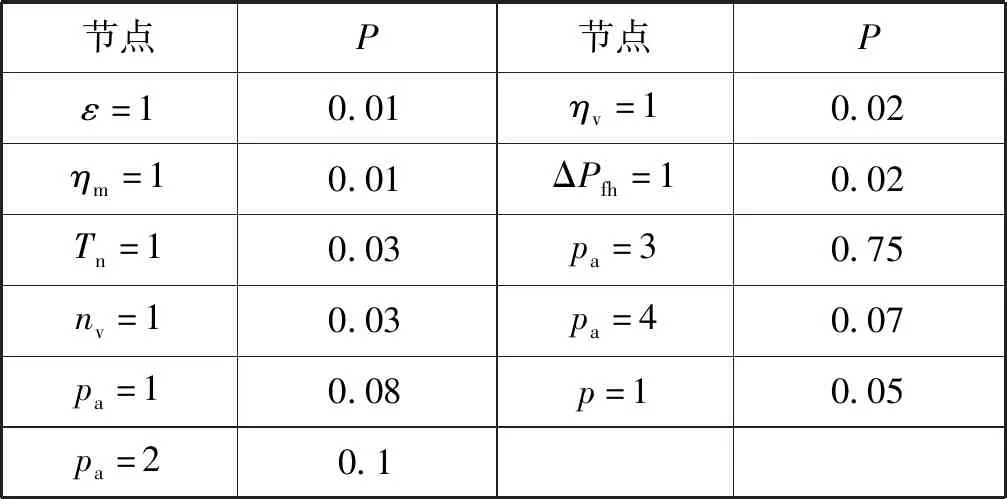
表3 邊緣概率結果

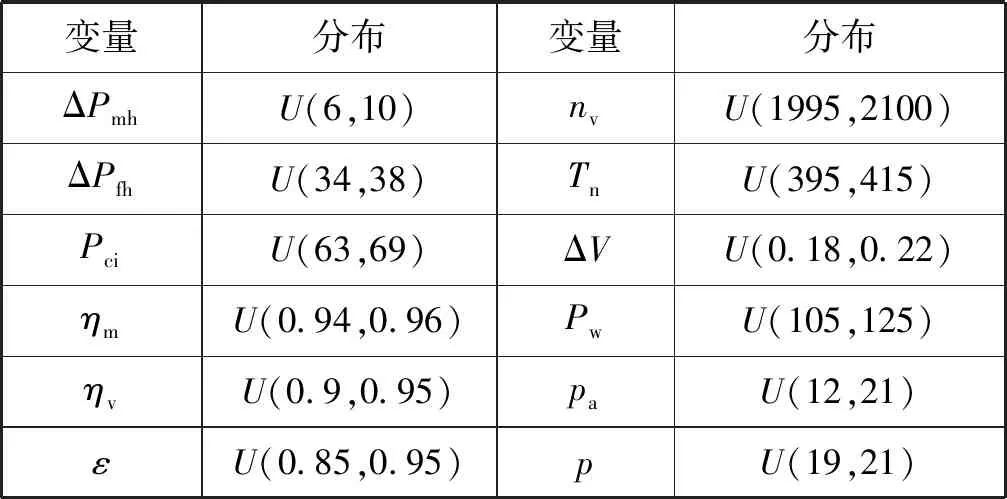
表4 節點的先驗分布

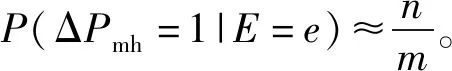
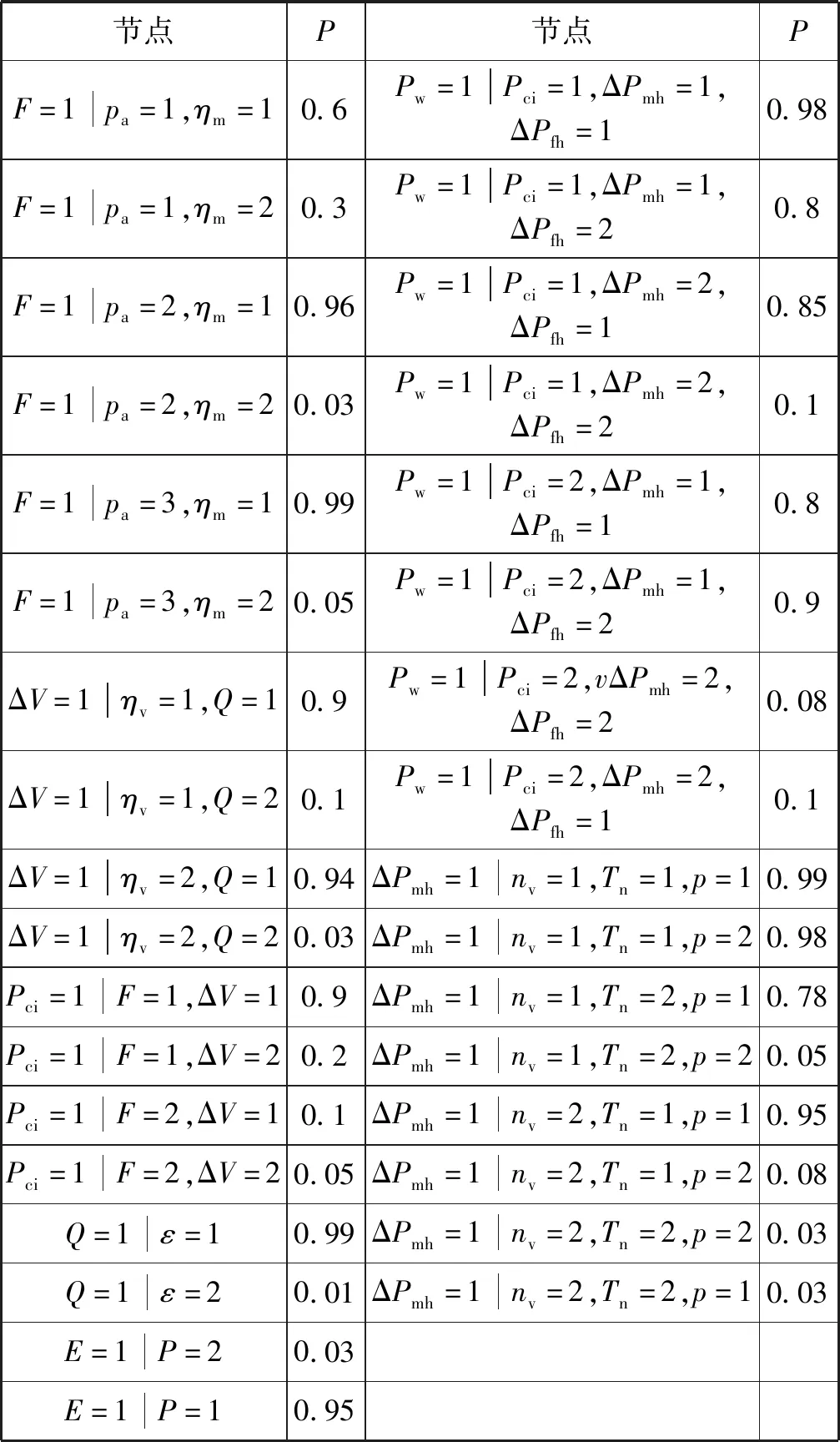
表5 節點條件概率結果

(3) 異常檢測與原因推理：本文選擇連接樹精確推理方法計算查詢變量的后驗概率，利用貝葉斯工具箱的推理算法計算結果。在計算模型中對擠壓機系統的異常情況的推理，假定目前可以通過觀測得到的證據變量擠壓油缸容積效率(ε)、主缸壓力(pa)、液壓泵的機械效率(ηm)的狀態都為異常狀態，其他傳感器數據丟失，未被記錄，則保持狀態不改變，推理擠壓機功率處于異常狀態的后驗概率為0.502 3，判定為發生異常。若判定異常發生，則采用控制變量法進行對比試驗，逐個改變當前輸入證據變量中某個變量的狀態，計算節點不同狀態下異常發生的概率。實驗結果如表6所示。

表6 實驗結果及對比實驗結果

(4) 重復試驗，分析A組、B組、C組的數據，計算本方法的正確率，如表7所示。

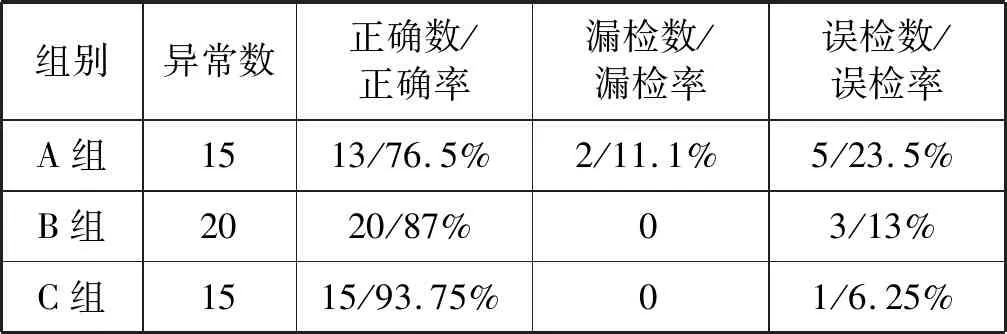
表7 貝葉斯網絡異常檢測算法結果

表6中的輸入d1、d2、d3分別代表擠壓油缸容積效率(ε)、主缸壓力(pa)、液壓泵的機械效率(ηm)。可以看出：(1)ε、pa、ηm的狀態都為異常狀態時，設備異常的概率為0.502 3；(2)ε、pa、ηm的狀態分別為異常狀態、異常狀態、非異常狀態時，設備異常的概率為0.500 1；(3)ε、pa、ηm的狀態分別為異常狀態、空載前進或快速后退階段、異常狀態時，設備異常的概率為0.485 8；(4)ε、pa、ηm的狀態分別為異常狀態、擠壓前進、異常狀態時，設備異常的概率為0.490 5；(5)ε、pa、ηm的狀態分別為非異常狀態、異常狀態、異常狀態時，設備異常的概率為0.501 9。由此可得，ε、pa、ηm的狀態分別為異常狀態、空載前進或快速后退階段、異常狀態時，后驗概率值與當前實際證據變量下得到的后驗概率之間的差值最大，即主缸壓力異常是設備異常主要原因。

4 結 語

(1) 針對影響擠壓機因素復雜且原因存在不確定性的問題，通過分析擠壓機能流機制構建的能耗模型而構建的貝葉斯網絡，較好地結合了專家知識與物理模型，避免了純粹依靠專家信息造成的信息錯誤率較高的問題，提高了貝葉斯網絡的可靠性。

(2) 針對傳統構建貝葉斯網絡的結構學習和參數學習兩大步驟，充分利用專業領域的知識，建立能耗模型，簡化結構學習步驟，極大地縮短了網絡構建周期。

(3) 結合專家知識與歷史數據得到貝葉斯網絡的條件概率表，通過仿真實驗得到貝葉斯網絡模型在異常檢測方面的效率在數據越來越豐富的情況下，會逐步上升并趨于穩定，基本可以檢測所有的異常點，漏檢率趨于0。印證了貝葉斯網絡的自學習能力使得它能較好處理實際應用場景中不完整數據集，且本文提出的通過擠壓機能耗模型構建貝葉斯網絡的方法有實際應用意義。