一種基于快速隨機(jī)投影的矩陣填充方法
馮雅莉 孫為軍
(廣東工業(yè)大學(xué) 廣東 廣州 510006)
0 引 言
近年來(lái),矩陣的使用越來(lái)越廣泛和越來(lái)越受重視,而矩陣分析方法的重要性也顯得越來(lái)越突出,例如矩陣分解、非負(fù)矩陣分解、低秩矩陣近似、矩陣填充等。而本文主要是關(guān)注其中的矩陣填充問(wèn)題,在實(shí)際問(wèn)題中,矩陣填充問(wèn)題主要表現(xiàn)在圖像和視頻處理、推薦系統(tǒng)、文本分析和機(jī)器學(xué)習(xí)[1-2]等方面。為了方便對(duì)數(shù)據(jù)進(jìn)行處理,一般我們會(huì)把數(shù)據(jù)轉(zhuǎn)化成矩陣的表示形式,但這些數(shù)據(jù)轉(zhuǎn)為矩陣后,經(jīng)常會(huì)面臨缺失,損毀和噪聲污染等問(wèn)題,所以如何恢復(fù)數(shù)據(jù)和對(duì)數(shù)據(jù)進(jìn)行去噪是我們需要解決和研究的問(wèn)題,而矩陣填充技術(shù)就是解決這類問(wèn)題的其中一種有效的方法。矩陣填充技術(shù)在圖像修復(fù)[3]、核磁共振圖像分割[4]、EEG信號(hào)處理、推薦系統(tǒng)[5]等領(lǐng)域中被廣泛應(yīng)用。
在近二十年里,矩陣填充技術(shù)越來(lái)越受關(guān)注。它的主要目的是通過(guò)矩陣中已知的元素來(lái)恢復(fù)未知的元素,通常利用矩陣中行與行或者列與列之間的線性關(guān)系對(duì)未知元素進(jìn)行估計(jì)和恢復(fù),所以需要被填充的矩陣是低秩的,這是矩陣填充的重要前提之一。近年來(lái),在矩陣填充領(lǐng)域中涌現(xiàn)了許多有效的算法,例如近鄰梯度下降算法[6](proximal gradient descent,PGD)、分塊坐標(biāo)下降算法[7]、矩陣空間Bregman迭代算法[8]、交替方向乘子法[9](alternating direction method of multipliers,ADMM),還有一些隨機(jī)優(yōu)化方法,例如隨機(jī)近鄰梯度下降算法(stochastic proximal gradient descent,SPGD)。
在解決實(shí)際的矩陣填充的問(wèn)題中,對(duì)矩陣進(jìn)行降維能夠大大減少矩陣填充在計(jì)算中的成本,常用的方法有主成分分析(principal component analysis,PCA)和奇異值分解(singular value decomposition,SVD)。大多矩陣填充方法都是利用傳統(tǒng)的SVD方法對(duì)原始矩陣進(jìn)行降維的,但是傳統(tǒng)的SVD的操作計(jì)算成本很高,所以不適用于大規(guī)模大尺寸的矩陣中。本文針對(duì)這個(gè)問(wèn)題,提出了一種快速的隨機(jī)投影方法,同時(shí)利用人工仿真數(shù)據(jù)和實(shí)際圖片像素?cái)?shù)據(jù)進(jìn)行了多個(gè)實(shí)驗(yàn),驗(yàn)證了本算法的可行性。
1 基礎(chǔ)知識(shí)
對(duì)于秩為r的矩陣X∈Rm×n,它的奇異值分解為:X=UΣVT,其中U∈Rm×r和V∈Rn×r滿足UTU=VTV=I。(I為r階單位矩陣),Σ=diag(σ1,σ2,…,σr)且其對(duì)角線上的元素滿足σ1≥σ2≥…≥σr>0,σi表示X的第i個(gè)奇異值。
X的Frobenious范數(shù)滿足:
式中:〈X,X〉表示X與X的內(nèi)積,trace(·)表示矩陣的跡算子。
2 快速矩陣填充方法
2.1 矩陣填充模型
秩是矩陣的一個(gè)重要的全局信息[9],它能體現(xiàn)出矩陣的信息冗余度,而矩陣能夠被充分地填充的前提條件是矩陣的信息是冗余的,其冗余度越低,填充難度就越高。所以矩陣填充的問(wèn)題一般是最小化矩陣的秩的問(wèn)題,其模型如下:
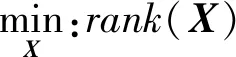
(1)
s.t.XΩ=MΩ
式中:X,M∈Rm×n,M可觀察的元素的索引存放在Ω集合中,而索引不在Ω集合中的元素均為未知的。由于函數(shù)rank(X)是非凸的,在實(shí)際優(yōu)化中求解非常困難。文獻(xiàn)[10]提出對(duì)rank(X)的最小化問(wèn)題可以轉(zhuǎn)化成對(duì)X的核范數(shù)最小化問(wèn)題,模型如下:
(2)
s.t.XΩ=MΩ

在過(guò)去使用核范數(shù)優(yōu)化模型的矩陣填充方法很多,例如奇異值閾值算法(Singular Value Thresholding,SVT)[11], 加速近端梯度算法(Accelerated Proximal Gradient,APG)[12],增廣拉格朗日乘子法(Augmented Lagrange Multipliers,ALM)。
本文引入一個(gè)新的變量Z,并把式(2)改寫成:
(3)
rank(Z)≤rank(X)

2.2 隨機(jī)快速矩陣填充方法
解式(3),一般采用SVD的方法,但是采用傳統(tǒng)的SVD的方法,計(jì)算的時(shí)間和計(jì)算復(fù)雜度都非常大和高,這不利于對(duì)大尺寸的矩陣進(jìn)行填充和處理,所以本文提出了一種快速的隨機(jī)投影方法。
假設(shè)一個(gè)矩陣X∈Rm×n,Ω和ΩC分別表示X矩陣中的已知和未知元素的索引集合。為了解式(3),我們可以采用交替最小二乘法對(duì)Z進(jìn)行更新。
本文方法分為以下幾個(gè)部分:
第一部分是對(duì)數(shù)據(jù)進(jìn)行預(yù)處理,初始化帶未知元素的矩陣X,把矩陣X的未知元素用獨(dú)立同分布的均值為0方差為1的高斯隨機(jī)分布賦值,如下所示:
第二部分,如果對(duì)X進(jìn)行傳統(tǒng)的SVD操作,則計(jì)算復(fù)雜度為Ο(min(m2n,mn2)),隨著矩陣的尺寸增大,計(jì)算的復(fù)雜度呈指數(shù)增長(zhǎng),所以需要對(duì)矩陣X進(jìn)行降維,方法如下:
C=X×H
(4)
式中:H∈Rn×r,且H是由獨(dú)立同分布的高斯隨機(jī)分布組成,至于r是如何選擇的可以參考文獻(xiàn)[13]。
第三部分,就是求出X的近似左奇異值矩陣:
U=C×V×Σ-1
(5)
式中:V是利用對(duì)CTC求特征向量獲得,Σ是通過(guò)對(duì)CTC求特征值開(kāi)平方根獲得。
第四部分,對(duì)X進(jìn)行矩陣填充,或者是低秩近似。因?yàn)閁在正常情況下是C的一個(gè)正交矩陣,所以UUT=I,而C是X的一個(gè)近似矩陣,所以我們以如下方式更新X:
X≈U×UT×X
(6)
第五部分是更新停止的條件的設(shè)定,本文采用均方差(mean squared error,MSE)來(lái)作為停止條件之一,定義如下:
(7)
當(dāng)MSE小于或者等于我們?cè)O(shè)定的閾值時(shí),或者迭代次數(shù)達(dá)到了我們?cè)O(shè)定的最大迭代次數(shù)時(shí),迭代停止。
本文的隨機(jī)投影算法的詳細(xì)步驟如算法1所示。
算法1基于隨機(jī)投影的矩陣填充算法
輸入:帶有未知元素的X矩陣(X∈Rm×n),估計(jì)的秩r,閾值t,最大迭代次數(shù)M
輸出:填充后的矩陣X
初始化:X中的未知元素都用獨(dú)立同分布的均值為0方差為1的高斯隨機(jī)分布賦值
循環(huán): 迭代次數(shù)n=1:M
步驟1C=X×H,其中H∈Rn×r
i.i.d.N(0,1)
步驟2 [V,d]=eig(CTC),其中V是C的右奇異矩陣,d是CTC的特征值組
步驟3U=C×V×Σ-1,其中
Σ=diag(diag(d).^0.5)
步驟4X=U×UT×X
當(dāng)MSE≤t或者n=M時(shí),迭代結(jié)束。
2.3 復(fù)雜度分析
算法1中,步驟1的計(jì)算復(fù)雜度為Ο(mnr),步驟2計(jì)算復(fù)雜度為Ο(nr+r2),步驟3 的計(jì)算復(fù)雜度為Ο(2nr2),步驟4的計(jì)算復(fù)雜度為Ο(m2r+m2n),所以本文算法迭代一次的計(jì)算復(fù)雜度大約為Ο((n+r)m2+mnr+2nr2+nr+r2)。
3 實(shí)驗(yàn)分析
將本文算法與SVT[11]、APG[12]和ALM[14]三個(gè)經(jīng)典的算法進(jìn)行比較,由于精確增廣拉格朗日乘子法(Exact Augmented Lagrange Multipliers,EALM)的計(jì)算成本較高,所以本文僅對(duì)ALM算法中的非精確增廣拉格朗日乘子法(Inexact Augmented Lagrange Multipliers,IALM)作比較。實(shí)驗(yàn)中,我們假設(shè)需要填充的矩陣M∈Rm×n,其秩為r=(r1,r2),實(shí)驗(yàn)的收斂條件為[15]:
(8)
或者是迭代次數(shù)達(dá)到設(shè)置的最大迭代次數(shù)。式中Vi表示我們需要迭代更新的第i個(gè)變量,ε表示收斂或者迭代停止的閾值,一般設(shè)定為10-5,本文中的最大迭代次數(shù)設(shè)置為100。
3.1 仿真數(shù)據(jù)實(shí)驗(yàn)
本節(jié)包含兩個(gè)部分:第一部分是需要被恢復(fù)的矩陣的秩不同的情況下,四個(gè)算法的恢復(fù)情況;第二部分是在不同采樣率下四個(gè)算法的恢復(fù)情況。對(duì)矩陣恢復(fù)有重要影響的兩個(gè)參數(shù)為恢復(fù)矩陣的秩和采樣率。我們用均方差(MSE)和運(yùn)行時(shí)間來(lái)作為對(duì)矩陣恢復(fù)效果的衡量標(biāo)準(zhǔn)。
第一部分,假設(shè)矩陣M∈R100×100,在其秩從2遞增至20間設(shè)計(jì)了10組實(shí)驗(yàn),采樣率p=0.5。實(shí)驗(yàn)結(jié)果如圖1所示。由圖1(a)可知,當(dāng)矩陣的秩在2~20之間時(shí),F(xiàn)RPMC方法的對(duì)矩陣的恢復(fù)的效果僅次于ALM算法,但圖1(b)中,F(xiàn)RPMC的恢復(fù)的速度比ALM快了一倍。在仿真實(shí)驗(yàn)中雖然APG和IALM的運(yùn)行速度相對(duì)比較快,但是它們矩陣恢復(fù)的相對(duì)誤差較高,即恢復(fù)的精度相對(duì)較低。
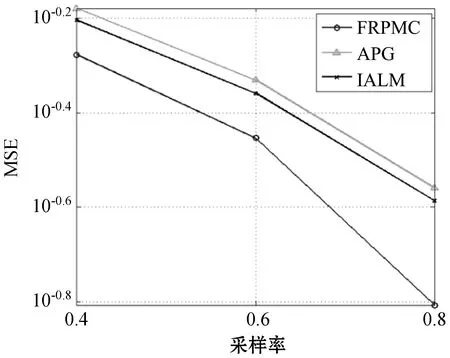
第二部分,假設(shè)矩陣M∈R100×100,矩陣的秩為5,在采樣率分別為0.4、0.6、0.8的條件下,用FRPMC、APG、IALM分別對(duì)矩陣進(jìn)行恢復(fù),結(jié)果如圖2所示。由圖2(a)可知,F(xiàn)RPMC方法的精度相對(duì)另外的兩種算法要高,而且隨著采樣率的增加,恢復(fù)的精度越高,恢復(fù)效果越好,即FRPMC在高采樣率的情況下,恢復(fù)效果比較顯著。

(a)

(b)圖1 不同算法在矩陣的秩不同的情況下矩陣恢復(fù)的結(jié)果
(a)
3.2 真實(shí)數(shù)據(jù)實(shí)驗(yàn)
本節(jié)主要利用對(duì)實(shí)際的缺失的黑白圖片的恢復(fù)來(lái)說(shuō)明FRPMC能夠?qū)崿F(xiàn)圖像恢復(fù)的功能。因?yàn)楹诎讏D片的像素相當(dāng)于一個(gè)二維的矩陣。實(shí)驗(yàn)將FRPMC算法與SVT、APG、EALM、IALM進(jìn)行比較,并用峰值信噪比(Peak Signal-to-Noise Ratio,PSNR)[17]作為衡量圖像恢復(fù)的效果的完整性的標(biāo)準(zhǔn),定義如下:
(9)

圖3中的6幅圖是分別在不同隨機(jī)采樣下生成的,采樣率從左至右分別是0.3、0.4、0.5、0.6、0.7、0.8。圖4的6幅圖則是圖3中相對(duì)應(yīng)的用FRPMC算法恢復(fù)后的圖像。圖4(a)是采樣率為0.3的情況下恢復(fù)后的圖像,從圖中可以清晰地看到房子的輪廓窗、房子在水中的倒影,說(shuō)明FPRMC方法能夠有效恢復(fù)帶有丟失數(shù)據(jù)的圖像。

(a) (b) (c) (d) (e) (f)圖4 經(jīng)過(guò)FRPMC處理后與圖3相對(duì)應(yīng)的恢復(fù)后的圖像
接下來(lái),隨機(jī)抽取來(lái)自Berkeley Segmentation數(shù)據(jù)集中的50幅圖來(lái)進(jìn)行實(shí)驗(yàn)。首先把這50幅彩圖進(jìn)行灰度化,使其變成黑白圖片,再進(jìn)行實(shí)驗(yàn)。
對(duì)這50幅處理后的黑白圖片進(jìn)行隨機(jī)采樣,采樣率分別是0.3、0.4、0.5、0.6、0.7、0.8,分別用FRPMC、SVT、APG和IALM四種方法進(jìn)行實(shí)驗(yàn)。實(shí)驗(yàn)假設(shè)最大迭代次數(shù)為100。實(shí)驗(yàn)結(jié)果如表1和表2所示。
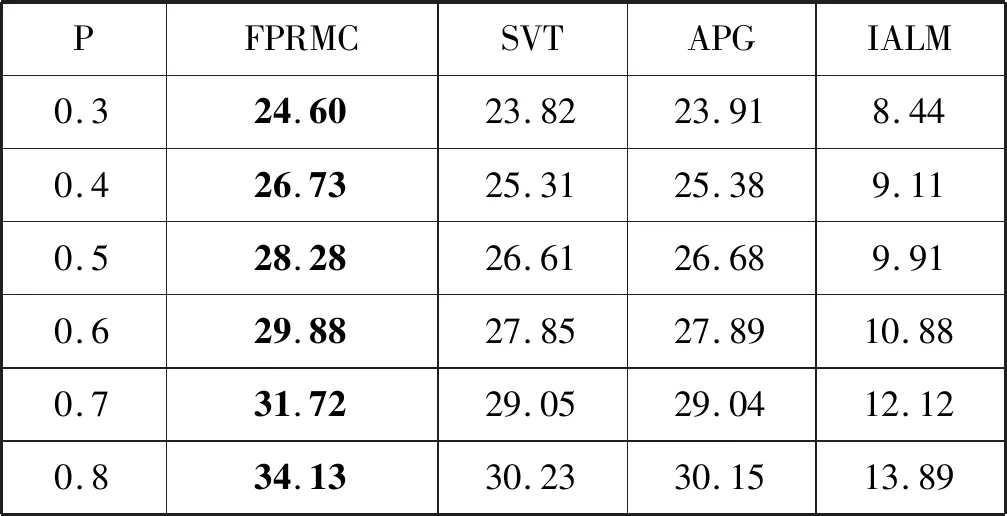
表1 在不同采樣率下四個(gè)算法的PSNR值
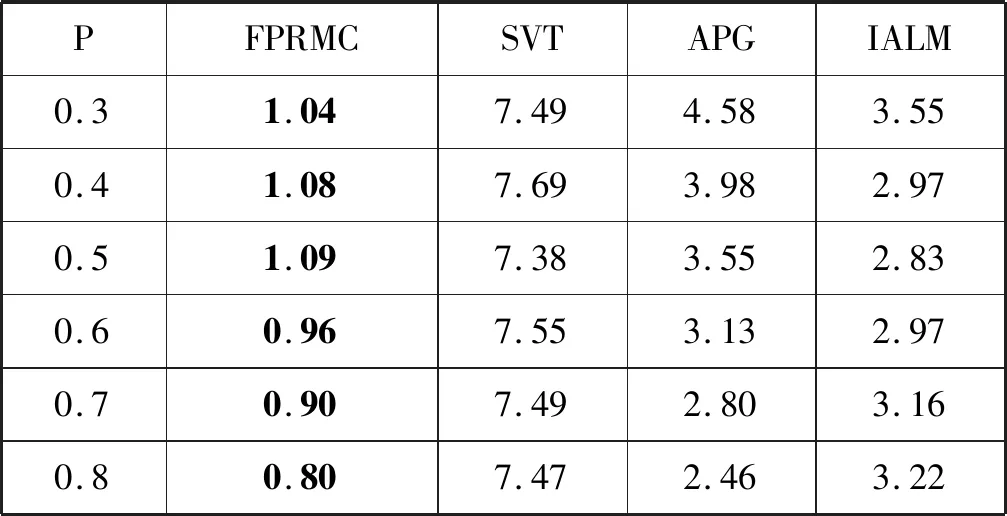
表2 在不同采樣率下四個(gè)算法的運(yùn)行時(shí)間
由表1可知,在圖像的尺寸為512×512的情況下,即FPRMC算法對(duì)黑白圖像恢復(fù)的PSNR是最高的,即效果最好的。由表2可知,F(xiàn)RPMC算法在實(shí)際圖像恢復(fù)中的速度也是最快的。
圖5為在采樣率為0.7的實(shí)驗(yàn)中隨機(jī)選取的5幅圖的實(shí)驗(yàn)情況。表3是圖5中對(duì)應(yīng)的5幅圖的恢復(fù)結(jié)果,分別是PSNR值和各個(gè)算法對(duì)應(yīng)的運(yùn)行時(shí)間。

(a) 原始圖片 (b) 加噪后圖片(P=0.7) (c) FRPMC算法 (d) SVT算法 (e) APG算法 (f) IALM算法圖5 隨機(jī)選取5幅圖的實(shí)驗(yàn)情況
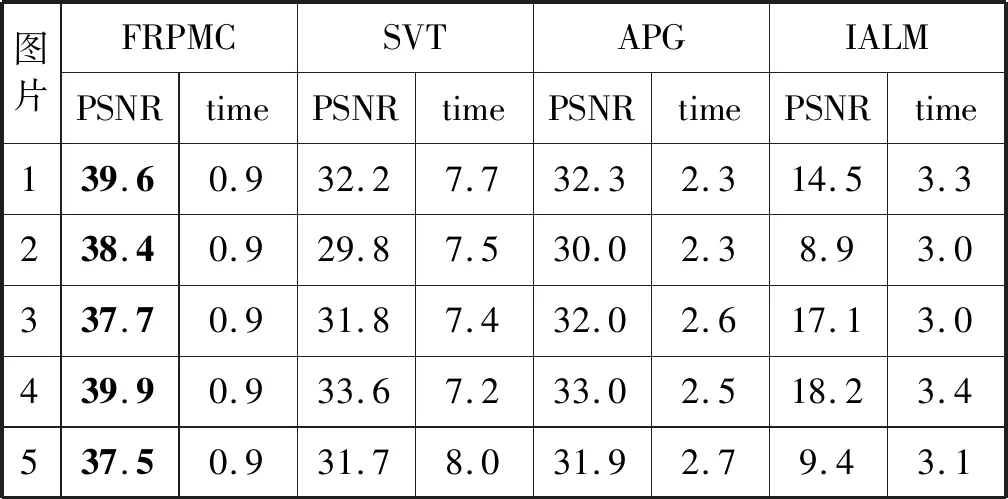
表3 圖5中5幅圖相對(duì)應(yīng)的PSNR值和對(duì)應(yīng)算法的運(yùn)行時(shí)間
4 結(jié) 語(yǔ)
傳統(tǒng)的矩陣填充方法很難避免標(biāo)準(zhǔn)的SVD的計(jì)算操作,而隨著矩陣維度的增加,SVD操作的計(jì)算復(fù)雜度呈指數(shù)增加,不適用于大規(guī)模、高維和高階的矩陣的處理。如何設(shè)計(jì)可擴(kuò)展的快速的算法是矩陣填充算法研究的核心。為了解決這個(gè)問(wèn)題,本文提出了一種快速的隨機(jī)投影方法,相對(duì)比于一般傳統(tǒng)的算法。FRPMC算法主要是利用隨機(jī)投影的方法對(duì)經(jīng)過(guò)隨機(jī)初試化的矩陣(帶有缺失值)進(jìn)行降維,然后再對(duì)其進(jìn)行特征值和特征向量的計(jì)算,利用SVD的計(jì)算模型來(lái)設(shè)計(jì)了一個(gè)矩陣的低秩近似的模型,對(duì)矩陣進(jìn)行恢復(fù),大大減少了計(jì)算的成本。
在今后的矩陣填充算法研究中,還將關(guān)注以下幾個(gè)方面:(1) 在確保精度的情況下,提高矩陣填充的速度;(2) 設(shè)計(jì)適合不同應(yīng)用場(chǎng)景的矩陣填充的模型;(3) 將矩陣填充擴(kuò)展到高維數(shù)組中,例如張量填充問(wèn)題上;(4) 研究可以利用已知元素來(lái)確定或者估計(jì)矩陣的秩的方法。

