(常熟理工學院數學與統計學院,江蘇 常熟 215500)(常熟外國語學校,江蘇 常熟 215500)

2018年青少年數學國際城市邀請賽和2001年普特南數學競賽中有兩道求面積的競賽題，都涉及到分點線三角形[1-2].三角形頂點與對邊分點的連線稱為三角形的分點線，由三角形3條分點線圍成的三角形稱為分點線三角形.筆者在題目給定的條件下解出了答案，接著考慮削弱條件后，看看能有什么結論，并把問題推廣到一般情況.

圖1

例1一個三角形被分割成4個小三角形與3個四邊形，如圖1所示，每個小三角形的面積都為1 cm2.請問四邊形CA0C0A1的面積為多少cm2?

(2018年青少年數學國際城市邀請賽隊際賽第8題)

解聯結AA0，C1C0.由S△AB0C1=S△A0B0C0，得S△AC1A0=S△AC0A0，從而

C1C0∥AA0，

同理可得

B1B0∥CC0，A1A0∥BB0,

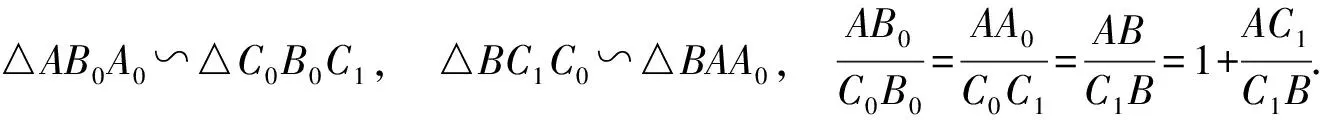
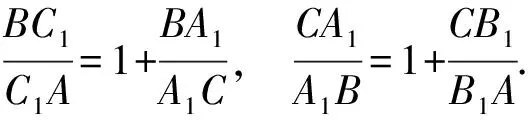
設點A1,B1,C1分別內分線段BC,CA,AB所成的比為正數a,b,c,則上面3個式子變為

消去b,c得

a2+a-1=0，

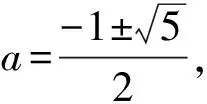
故3個四邊形面積都相等.設四邊形CA0C0A1的面積為xcm2，則

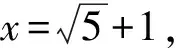
解答本題后再進一步思考，如果在條件中除去小△A0B0C0，而其余3個小三角形的面積相等，又會有怎樣的結果呢？

例2如圖1所示,在△ABC中，設點A1,B1,C1分別內分線段BC,CA,AB所成的比為正數a,b,c，△ABC的面積為Scm2，AA1,BB1,CC1圍成△A0B0C0，當△AB1C1，△BA1C1，△CB1A1的面積相等時，求△A0B0C0的面積.

解△ABA1被直線C1B0C所截，由梅涅勞斯定理得

由3個小三角形等積，得連等式

這兩個連等式是關于字母a,b,c的輪換對稱式，因此猜想連等式成立時，有a=b=c.

下面用反證法證明這一結論：假設a≥b≥c(兩個等號不同時成立，下同)，由a,b,c為正數知

綜上所知，當3個小三角形等積時，a=b=c.

又S△A0B0C0=S-S△ABC0-S△BCA0-S△CAB0，經過運算得

圖2

例3如圖2所示，已知△ABC的面積為1，點E,F,G分別在邊BC,CA,AB上，AE平分線段BF于點R，BF平分線段CG于點S，CG平分線段AE于點T，求△RST的面積.

(第62屆普特南數學競賽A-4題)

λ1λ2+λ1+1=λ2λ3+λ2+1=λ3λ1+λ3+1=2,

本題通過設三角形各邊上的點得到邊所分成的比，再利用已知的中點條件代入，求出這些比值，從而計算出所求三角形的面積.可以考慮如果R分BF，S分CG，T分AE所成的比是任意比，并且各不相同，那么如何算出△RST的面積呢？下面來探究這個問題.

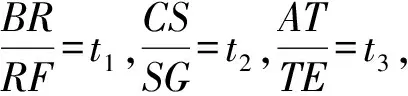
解與前面例3的過程相同，在△BCF中，由梅涅勞斯定理可得t1=λ1(1+λ2)，同理可得

t2=λ2(1+λ3)，t3=λ3(1+λ1).

解方程組

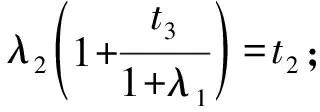
(4)

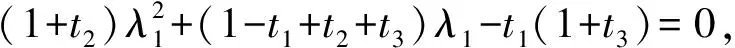
當上式的根號前取負號時，λ1為負數，不符合題意故舍去.同理可得

將解方程得到的λ1,λ2,λ3的值代入上式，即可求得△RST的面積.