數據與模型驅動的水泥生料分解率軟測量模型

喬景慧 柴天佑

復雜工業過程運行優化控制[1?2]需要準確檢測與生產過程中產品質量、產量、效率、能耗等指標相關的難以直接測量的過程參數[3?4],如水泥熟料生產過程中的生料分解率(Raw meal decomposition ratio,RMDR)、回轉窯燒成帶溫度、燒成帶長度、回轉窯內物料停留時間、廢氣氮氧化物及氧含量、熟料游離氧化鈣含量[5?6].這些過程參數的實時檢測一直是水泥熟料生產過程亟待解決的難題.產品質量指標生料分解率決定臺時產能、熟料熱耗、回轉窯負荷率及預熱器C5 下料管堵塞概率[7].實際中,生料分解率由人工取樣每隔1 小時檢測一次,這樣影響生產的正常運行.因此,水泥生料分解過程生料分解率的研究是至關重要的.

實際中,為了獲得生料分解率軟測量值,需要采集離線及在線輔助變量數據.因此,需要對這些輔助變量進行異常值檢測,常用的檢測方法有基于距離的異常值檢測[8].然而它沒有考慮局部密度的變化,僅適用于全局異常值檢測,不適用于局部異常值檢測.目前,基于密度的異常值檢測方法得到廣泛應用,如文獻[9?10],但是對于未知樣本計算概率密度是很困難的.因此,采用不計算概率密度而直接進行密度比評估的Kullback-Leibler(KL)散度密度比的異常值檢測方法[11].

對于水泥生料分解過程的研究,文獻[12]提出了遞歸限定記憶主元分析與最小二乘支持向量機結合的生料分解率軟測量模型.采用魯棒3σ檢測采樣數據的異常值,選擇高斯核函數與線性核函數.但是,當生料成分穩定時,沒有采用機理模型計算生料分解率.文獻[13]建立了基于二維數據投影映射的生料分解率動態軟測量模型,同時進行了實驗室仿真驗證.文獻[14]提出了層級建模方法,建立了適用于大型回轉窯的混合的二維和三維計算流體動態模型.文獻[15]建立了一個基于數據驅動的分解率仿真實驗模型,通過調整分解爐給煤量控制生料分解率.文獻[16]為了分解爐優化設計,通過分析歷史數據和經驗數據建立了多個線性回歸模型.

1 生料分解過程工藝描述及質量指標

1.1 生料分解過程工藝描述

生料分解過程工藝流程如圖1 所示.生產過程包括5 級預熱器、1 臺分解爐和1 臺回轉窯.生料在5 級預熱器預熱后進入分解爐,分解率達到85%～94%.分解后的生料由第5 級預熱器進入回轉窯,生料在經過預熱器和分解爐后被逆向前進的熱氣流加熱,來自煤粉倉的煤粉與三次風混合一起噴入分解爐.圖1 中變量及符號如表1 所示.

表1 圖1 中各變量及符號的含義Table 1 The meaning of variables and symbols in Fig.1

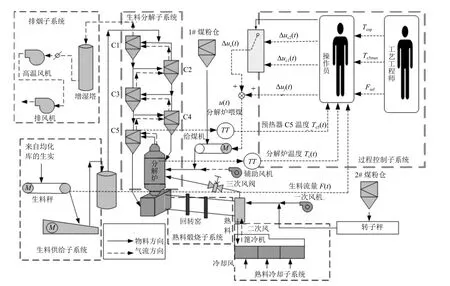
圖1 生料分解過程工藝流程及控制現狀Fig.1 Process flow diagram and current control for raw meal calcination process

實際生產中,沒有在線分析儀表檢測生料分解率.因此,生料分解率只能由人工離線檢測,即每隔1 小時在回轉窯窯尾取樣一次,采用二氧化碳體積法測定生料分解率[17],檢測周期為2 小時,嚴重滯后.由于生料分解率影響臺時產能、熟料熱耗及回轉窯負荷率.因此,必須建立生料分解率的在線模型.

1.2 生料分解過程質量指標

在工業生產中,衡量分解爐工作效率及安全的重要指標是生料分解率,它是指生料經過分解爐和預熱器C5 后,分解成氧化物的碳酸鹽占總碳酸鹽的百分比.生料分解率決定生料分解過程的產能指標—臺時產能、熟料熱耗和回轉窯負荷率,決定生料分解過程的安全—預熱器C5 下料管堵塞概率.

1)生料分解率與臺時產能的關系

臺時產能是單位時間(小時)內生產熟料的質量(噸),如式(1)所示.

其中,G代表設備熟料小時產能(t/h),γ表示生料分解率(表示為小數形式),D和L分別代表回轉窯酮體直徑和回轉窯長度(m).

臺時產能G與生料分解率γ的關系曲線如圖2所示.式(1)和圖2 表明,臺時產能G與生料分解率γ成正比,即臺時產能G隨著生料分解率γ的增加而增大.

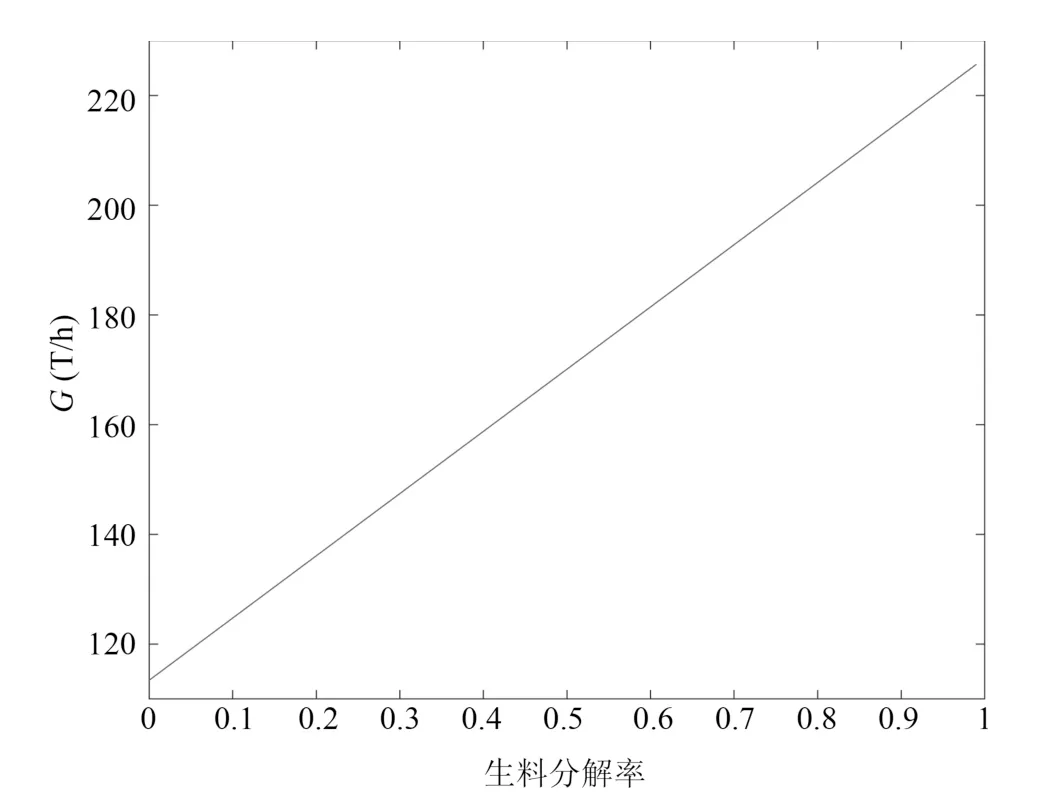
圖2 臺時產能與生料分解率關系曲線Fig.2 The relationship curve between the production hourly and raw meal decomposition ratio

2)生料分解率影響熟料熱耗

在實際生產中,生料分解率γ偏高時,會使預熱器C5 下料管堵塞,甚至使生產停產;生料分解率γ過低,會使生料預熱效果差,根據式(2)將增加下一工序(即回轉窯內燒結)的熱負荷即熟料熱耗,熟料熱耗q與生料分解率γ的關系曲線如圖3 所示.

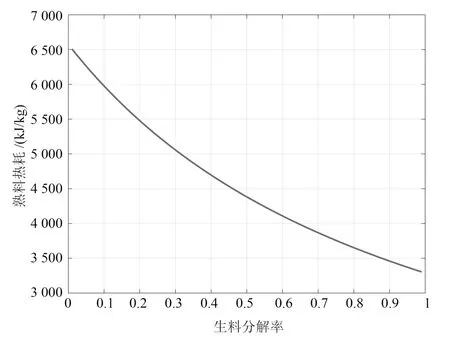
圖3 熟料熱耗與生料分解率關系曲線Fig.3 The relationship curve between clinker heat consumption and raw meal decomposition ratio

其中,Q為燃料熱值(kJ/kg),M代表每小時入回轉窯燃料消耗量(t/h),R是入回轉窯燃料比(用小數表示),q表示熟料熱耗(kJ/kg 熟料),γ為生料分解率(表示為小數形式),D和L分別代表回轉窯酮體直徑和回轉窯長度(m).

圖3 表明,在煤粉燃料熱值Q、每小時入回轉窯燃料消耗量M為定值時,回轉窯內熟料熱耗q與生料分解率γ成反比.因此,當生料分解率低于實際值,回轉窯內熟料熱耗q將增加.但是,實際中隨著生料成分及入窯分解率的變化,入回轉窯和分解爐的煤粉質量是發生變化的,根據式(2),可以得出熟料熱耗q與回轉窯耗煤量M和生料分解率γ之間的關系曲線,如圖4 所示.

圖4 表明,在煤粉燃料熱值Q為定值時,回轉窯內熟料熱耗q與每小時入回轉窯燃料消耗量M成正比,與生料分解率γ成反比.

3)生料分解率影響回轉窯負荷率

實際生產中,生料分解率γ還影響回轉窯負荷率?.為了穩定整個生產熱工工況,要求回轉窯內物料負荷率盡量保持不變,一般要求負荷率?=5%～13%,如式(3)～(5)所示.

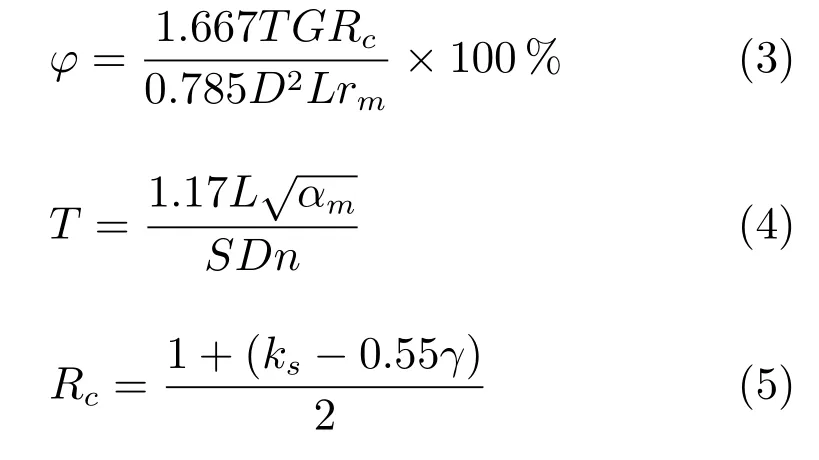
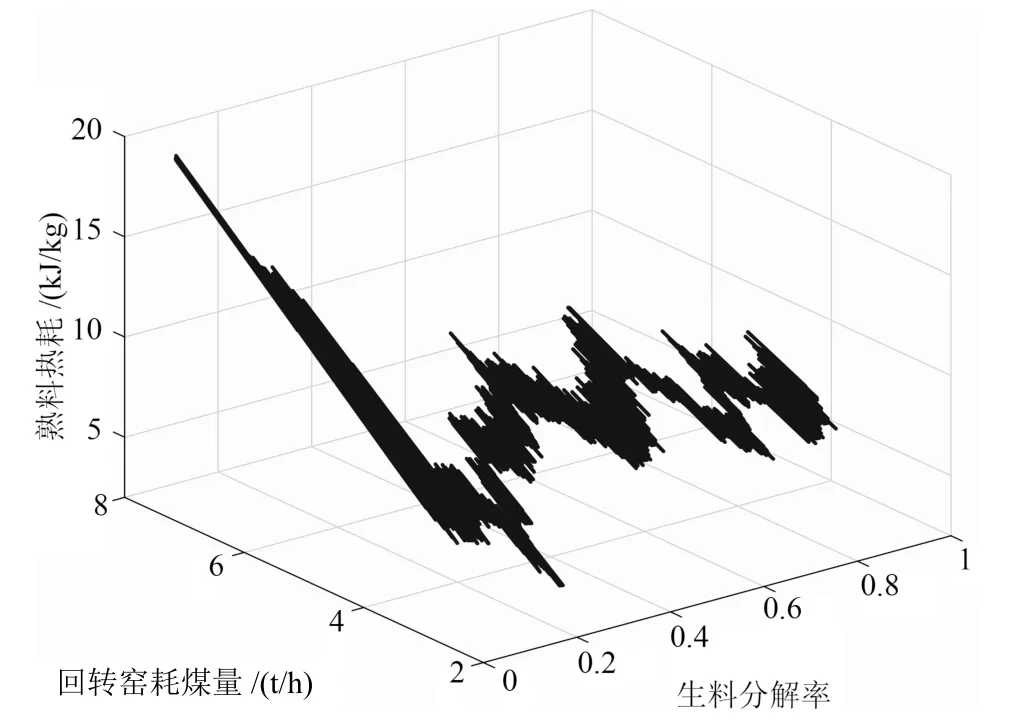
圖4 熟料熱耗與生料分解率和回轉窯耗煤量關系曲線Fig.4 The relationship curve among the clinker heat consumption and raw meal decomposition ratio and feed coal of rotary kiln

其中,?表示負荷率(%),G為設備熟料小時產能(t/h),Rc為煅燒1 kg 熟料所需回轉窯內物料量,T為物料在回轉窯內停留時間(min),γ為生料分解率(表示為小數形式),D和L分別代表回轉窯酮體直徑和回轉窯長度(m).rm代表回轉窯內物料平均堆積密度(kg/m3),S和αm分別代表回轉窯斜度和物料自然休止角(度),n是回轉窯轉速(r/min),ks為實際物料消耗量.

根據式(3)～(5),回轉窯內物料負荷率?與生料分解率γ和回轉窯轉速n之間的關系如圖5 所示.圖5 表明,回轉窯負荷率?與回轉窯轉速n成反比,隨生料分解率γ的增大而增大.

圖5 回轉窯負荷率與生料分解率和回轉窯轉速關系曲線Fig.5 The relationship curve among the load rate and raw meal decomposition ratio and rotary kiln speed

根據式(1)～(5),生料分解率γ影響回轉窯臺時產能G,熟料熱耗q和負荷率?.因此,必須精確確定生料分解率.

1.3 生料分解率實際檢測

在工業生產中,衡量分解爐工作效率的重要指標是生料分解率,它是指生料經過分解爐和預熱器C5 后,分解成氧化物的碳酸鹽占總碳酸鹽的百分比.這樣提高入回轉窯的生料分解率是減輕回轉窯內熱負荷和提高產量的關鍵.但是生料分解率控制過高,會產生預熱器C5 下料管堵塞現象,使生產停產;反之,生料分解率控制過低,沒有充分發揮分解爐的作用,會使得生料預熱效果差且加大回轉窯的熱負荷,降低產能.因此,分解率指標廣泛地應用于實際生產過程中.

實際生產中,實驗室檢測人員每間隔1 小時在窯尾取樣一次,通常采用表觀分解率γ衡量生料分解率,如式(6)所示.

其中,L1和L2分別代表出均化庫生料CO2的百分含量和預熱器C5 下料管入回轉窯生料CO2的百分含量(%).

根據式(1)和式(6),調度員計算臺時產量G隨出均化庫生料CO2的百分含量L1和預熱器C5 下料管入回轉窯生料CO2的百分含量L2之間的關系曲線,如圖6 所示.由圖6 可知,臺時產能G與出均化庫生料CO2的百分含量L1成正比,而與預熱器C5 下料管入回轉窯生料CO2的百分含量L2成反比.

圖6 臺時產能與出均化庫生料CO2的百分含量和預熱器C5 下料管入回轉窯生料CO2的百分含量關系曲線Fig.6 The relationship curve among the production hourly and percentage of CO2from homogenization and the percentage of CO2in raw material from the preheater C5 tube

2 數據與模型驅動的水泥生料分解率軟測量模型

2.1 生料分解率軟測量模型輔助變量選擇

生料分解率影響臺時產能G、熟料熱耗q和回轉窯負荷率?,同時決定預熱器C5 下料管堵塞的概率.但是實際生產中,人工每隔1 小時檢測一次生料分解率.為了實時獲得生料分解率軟測量模型,必須選擇正確的輔助變量,采用文獻[12]中表1 的變量作為輔助變量.

2.2 生料分解率軟測量模型結構

為了解決生料分解率離線化驗周期長,增加臺時產能G,穩定回轉窯內負荷率?及降低熟料熱耗q,本文提出了基于數據與模型驅動的生料分解率軟測量模型,如圖7 所示.

圖7 中,x1,x2,···,xd和α1,α2,···,αb分別為層級S 核函數的輸入變量及隱含層與輸出層的權值,圖7 中其他符號的含義如表2 所示.

如圖7 所示,數據與模型驅動的生料分解率軟測量模型由基于KL 散度密度比的異常值檢測、基于機理模型的生料分解率模型、基于層級S 核函數的生料分解率模型、生料分解率離線檢測模型和基于模糊模型的協調因子組成,各部分功能如下所示.

表2 圖7 中各變量的含義Table 2 The meaning of variables in Fig.7

1)基于KL 散度密度比的異常值檢測

圖7 數據與模型驅動的水泥生料分解率軟測量模型Fig.7 The cement raw meal decomposition ratio model based on data and model

將采集的生料中氧化鈣含量、三氧化二鐵含量、二氧化硅含量及三氧化二鋁含量及分解爐溫度等,詳細輔助變量參見文獻[12]的表1,采用估計概率密度比ω(x)并使用線性參數模型近似ω(x)的方法,進行異常值檢測.

2)基于機理模型的生料分解率模型

當生料中的成分穩定時,在分解溫度范圍內,可以由式(16)得出生料分解率γm.

3)基于層級S 核函數的生料分解率模型

實際生產中,每一批生料的成分及配料后生料成分是變化的.同時,生料分解率會隨著生料中氧化鈣含量、三氧化二鐵含量、二氧化硅含量及三氧化二鋁含量成非線性變化的.采用模仿人類腦細胞的S 型核函數作為輸入輸出函數,建立基于層級S 核函數的生料分解率模型,計算生料分解率fθ(x).

4)生料分解率離線檢測模型

實際生產中,實驗室檢測人員每隔1 小時在窯尾取樣一次,檢測出均化庫生料及預熱器C5 下料管入回轉窯生料CO2百分含量,根據式(6)離線計算生料分解率γa.

5)基于模糊模型的協調因子

生料分解過程中,生料成分有的在正常范圍內,有的成分不在正常范圍內.因此,采用基于模糊模型的協調因子對γm加權,計算加權后的生料分解率.

2.3 數據與模型驅動的水泥生料分解率軟測量模型

2.3.1 基于KL 散度密度比的異常值檢測

生料中氧化鈣含量、三氧化二鐵含量、二氧化硅含量及三氧化二鋁含量變化時,會影響生料的實際分解率[18].根據圖3,當實際分解率減小或增大時,熟料在回轉窯內的熱耗相應地增大或降低.因此,必須根據生料成分及時預測生料的分解率.為了有效的檢測采樣值的異常數據,使用基于KL 散度密度比的方法檢測異常數據.

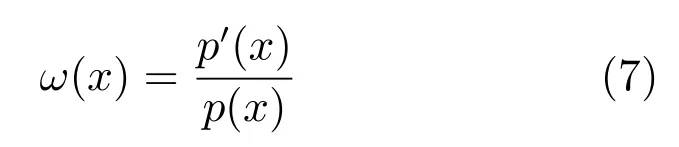
其中,對于正常樣本ω(x)的值接近1,對于異常樣本ω(x)的值與1 相差較大的值.但是,對于計算得到的密度比ω(x),如果測試樣本的概率密度p(x)值較小時,式(7)中概率密度p＇(x)的誤差會相應地增大.因此,采用估計概率密度比ω(x)并使用線性參數模型近似ω(x)[19],如式(8)所示.

其中,αT=(α1,α2,···,αk)代表參數向量,ψ(x)=(ψ1(x),ψ2(x),···,ψk(x))T是非負的基函數向量.因此,通過調整參數α使ωα(x)p(x)趨近于p＇(x).對于?p＇(x)≥0,p(x)≥0,定義廣義KL 散度函數如式(9)所示.

使用ωα(x)p(x)代替式(9)中的p(x),得

其中

因此,式(10)簡化為

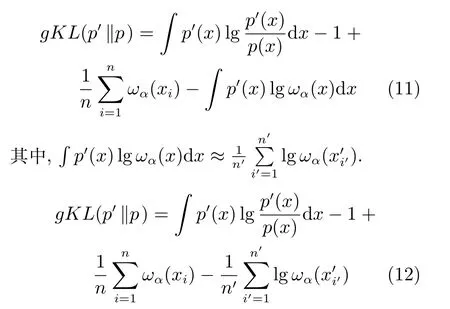
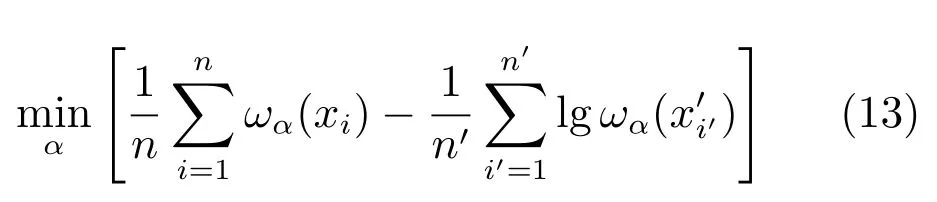
式(8)中的密度比選擇高斯核函數,如式(14)所示.

2.3.2 基于機理模型的生料分解率模型

在生料分解過程中,生料在分解爐內發生分解反應,如式(15)所示[20],分解爐溫度與生料分解率之間的動態數學模型如式(16)所示[18].

其中,?Q 表示碳酸鈣分解過程吸收熱量.

其中,k0=6.078×107,E=2.05×105(J/mol),式(16)中參數的含義如表3 所示.

表3 式(16)中參數的含義Table 3 The meaning of variables in(16)

生料分解率與分解爐溫度之間的曲線如圖8 所示.

圖8 生料分解率與分解爐溫度關系曲線Fig.8 The relationship curve between the raw meal decomposition ratio and calciner temperature

圖8 表明,生料分解率與分解爐溫度具有較強的非線性,生料在分解爐內正常分解溫度為850～890?C.因此,在生料中的成分穩定時,在分解溫度范圍內,可以由式(16)得出生料分解率.但是,生料中的成分是變化的,可以采用基于層級S 核函數驅動的生料分解率模型.

2.3.3 基于層級S 核函數的生料分解率模型

當生料的成分氧化鈣含量、三氧化二鐵含量、二氧化硅含量及三氧化二鋁含量均在正常值范圍內波動時,采用基于機理模型的生料分解率建模.但是,每一批原料中生料的成分及配料后生料成分是變化的.同時,生料分解率會隨著生料中氧化鈣含量、三氧化二鐵含量、二氧化硅含量及三氧化二鋁含量成非線性變化的.生料分解率與生料成分之間的關系曲線如圖9 所示.

圖9 生料分解率與生料成分關系曲線Fig.9 The relationship curve between the raw meal decomposition ratio and raw meal components

為了解決生料成分波動對生料分解率的影響,采用模仿人類腦細胞的S 型核函數作為輸入輸出函數[21],建立基于層級S 核函數的生料分解率模型,模型輸出如式(17)所示.

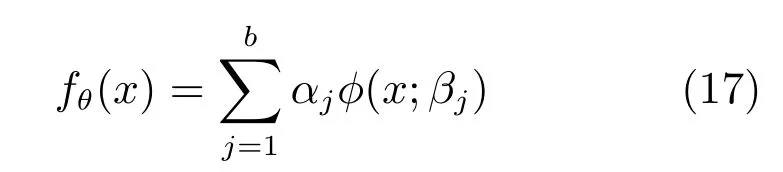
其中,αj代表模型參數,fθ(x)是關于的非線性函數,α=(α1,α2,···,αb)T,φ(x;β)為S 型核函數,如式(18)所示.

式(18)可簡化為

采用文獻[21]隨機梯度下降法訓練層級模型,定義性能函數如式(20)所示.

其中,θ=(αT,wT,ζ)T∈R3,γa為生料分解率實際檢測值,分別計算J(θ)對αj,wj和ζj的偏導數,即?J(i),如式(21)所示.

隨機梯度算法中,取式(24)負梯度方向為搜索方向.則隨機梯度下降法的迭代式如式(25)所示.

式(25)中,在第k次的迭代初始點θ(k)和搜索方向d(k)已經確定的情況下,式(20)是關于步長μ >0的一維函數,即

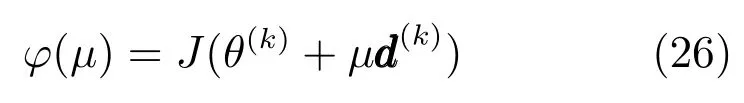
最優步長μk利用式(27)求得

2.3.4 基于模糊模型的協調因子λ

由圖9 可知,生料中氧化鈣含量、三氧化二鐵含量、二氧化硅含量及三氧化二鋁含量與生料分解率成非線性關系.當生料中的四種成分都在正常波動范圍內時,采用基于機理的生料分解率模型;否則,采用基于層級S 核函數的生料分解率模型.但是,實際中生料中有的成分在正常波動范圍,有的成分不在正常范圍內,生料中各成分與生料分解率之間的關系如式(28)所示[18].

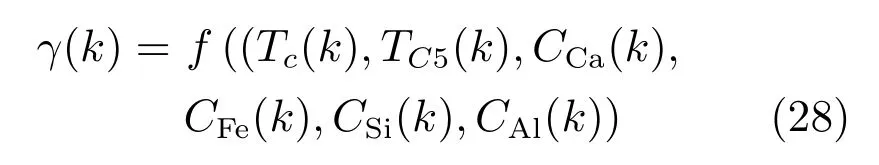
式中,γ(k)表示生料分解率,Tc(k)和Tc5(k)分別代表分解爐溫度和預熱器C5 出口溫度,CCa(k),CFe(k),CSi(k)和CAl(k)分別表示生料中氧化鈣含量、三氧化二鐵含量、二氧化硅含量及三氧化二鋁含量.

當分解爐溫度Tc(k)和預熱器C5 出口溫度Tc5(k)不變時,生料中四種成分(CCa(k),CFe(k),CSi(k)和CAl(k))分別與生料分解率存在如圖10所示的運行關系.

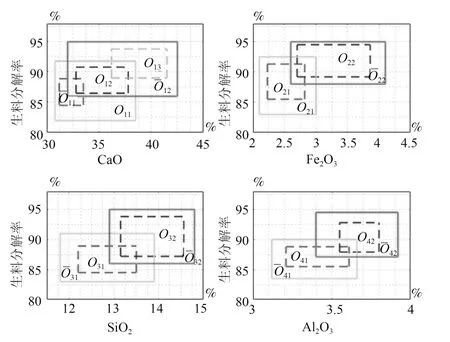
圖10 生料成分與生料分解率關系曲線Fig.10 The relationship curve between the raw meal decomposition ratio and raw meal components

圖10 中,Oij(i=1,···,4;j=1,2,3)表示目標運行區間,(i=1,···,4;j=1,2)表示最大運行區間;令Zγ,i=[γa(0)?γi,γa(1)?γi,···,γa(N)?γi]是生料分解率實際檢測值γa(k)(k=0,···,N)與Oij(i=1,···,4;j=1,2,3)穩態運行點γi的偏差組成的向量.根據文獻[22]基于多模型的生料分解率輸出值為γm,則模型輸出γm與γi的偏差為vi(k),即vi(k)=γm ?γi,則有Zv,i=[v(0),v(1)i,···,v(N)],則目標運行區間Oij(i=1,···,4;j=1,2,3)的范圍為

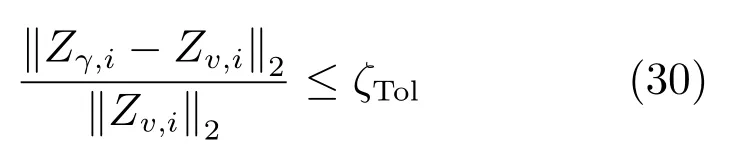
這樣,目標運行區間Oij(i=1,···,4;j=1,2,3)和最大運行區間(i=1,···4;j=1,2)的每一個點可以表示為

結合圖10,目標運行區間的相鄰兩個運行區間的關系如式(33)所示.

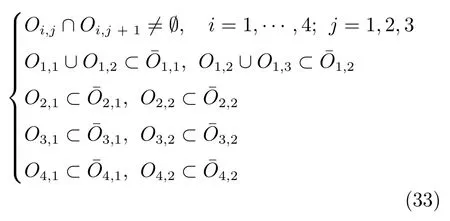
式(33)及圖10 表明,當生料中某一成分為一個固定值(如CCa(k)=31.5%)時,生料分解率處于目標運行區間O11和O12,其中O12為正常工況,采用機理模型計算生料分解率;處于O11工況時,采用基于層級S 核函數的生料分解率模型計算生料分解率.因此,采用基于模糊模型的協調因子計算生料分解率,如圖11 所示.令生料中四種成分CCa(k),CFe(k),CSi(k)和CAl(k)的設定值分別為CCaSP(k),CFeSP(k),CSiSP(k)和CAlSP(k),其中e1(k)=CCa(k)?CCaSP(k),e2(k)=CFe(k)?CFeSP(k),e3(k)=CSi(k)?CSiSP(k)和e4(k)=CAl(k)?CAlSP(k).

1)e1(k),e2(k),e3(k),e4(k)和λ(k)的模糊化

由圖11 可知,e1(k),e2(k),e3(k)和e4(k)的量化因子分別為和k4λ(k)的比例因子則E1(k),E2(k),E3(k),E4(k)和λ(k)分別為

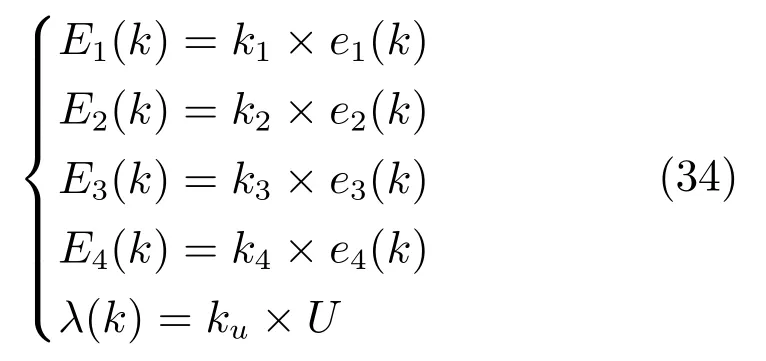
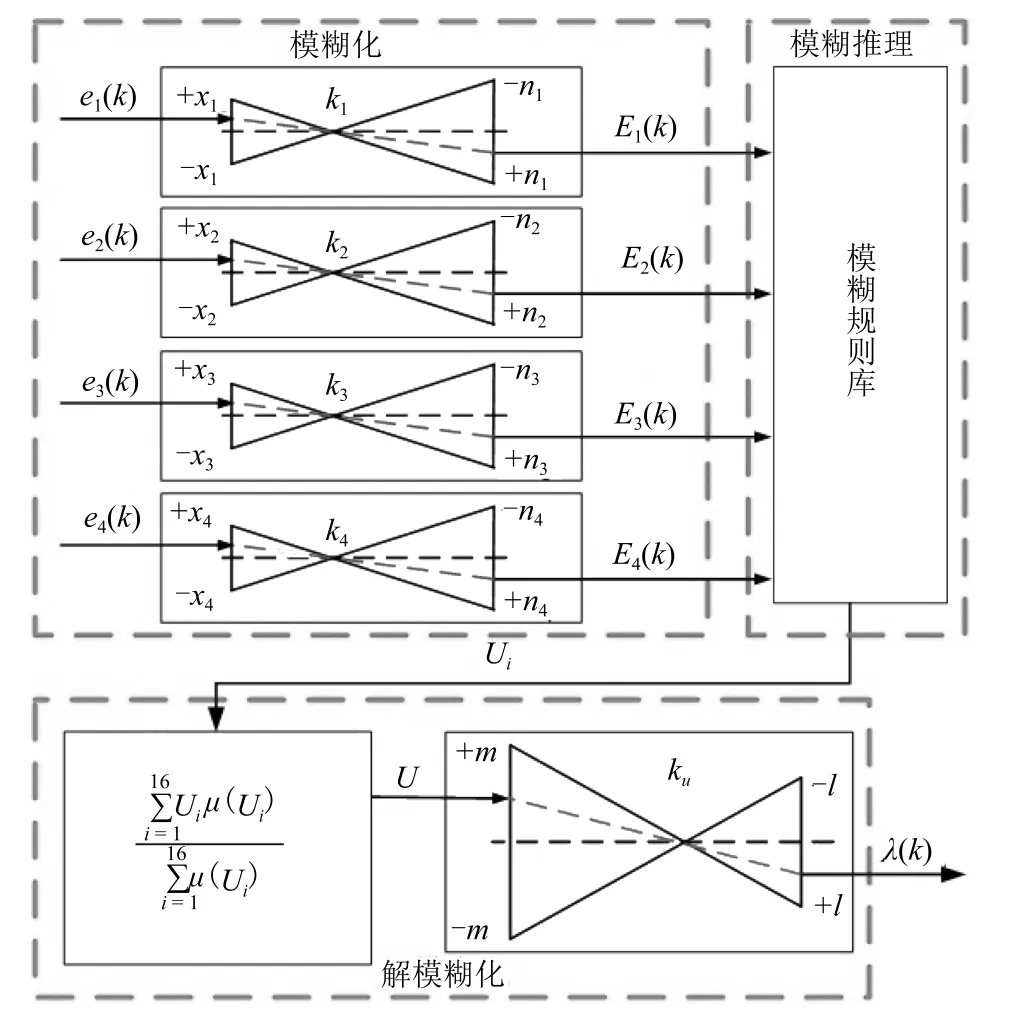
圖11 基于模糊模型的協調因子結構Fig.11 The structure of coordination factor based on fuzzy model

其中,E1(k),E2(k),E3(k)和E4(k)在各自論域上的模糊子集個數為5,分別為負大(NB),負小(NS),零(ZE),正小(PS)和正大(PB).

2)模糊推理

采用文獻[23]方法建立模糊規則,如式(35)所示.

其中,p=4,q=5,i=1,2,3,···,16,選擇E1(k),E2(k),E3(k),E4(k)和U的隸屬函數為對稱三角形隸屬函數,如圖12 所示.輸入E1(k),E2(k),E3(k)和E4(k)共有規則數量如式(36)所示.

其中,Ni=5,采用圖13 所示的模糊推理過程.

采用重心法解模糊化得到協調因子.由圖12 可知,對于任何E1(k),E2(k),E3(k)和E4(k)所對應的模糊子集的最大個數為16.因此,只需要計算這16 個模糊子集所對應的輸出模糊集的隸屬度μ(Ui)(i=1,2,···,16),如式(37)所示.

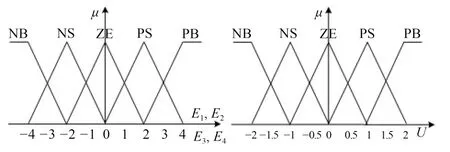
圖12 誤差E1, E2, E3和E4及輸出U 的隸屬函數Fig.12 The membership functions of E1, E2, E3and U

圖13 模糊推理過程Fig.13 The fuzzy inference process

式中,μ(Ui)代表第i條規則輸出量模糊集的隸屬度,Ui是第i條規則結論部分隸屬函數的中心.

根據圖11 及式(37),協調因子λ(k)如式(38)所示.

3 仿真驗證

為了驗證本文提出的水泥生料分解過程生料分解率軟測量模型的有效性,首先在實驗室進行了基于數據與模型驅動的水泥生料分解率軟測量模型仿真實驗,在第4 節中進行了工業應用驗證.

基于KL 散度密度比的異常值檢測模塊中,在線檢測數據有分解爐溫度、預熱器C5 出口溫度、回轉窯窯尾溫度、C5 下料管溫度等;離線檢測數據有生料中氧化鈣含量、三氧化二鐵含量、二氧化硅含量及三氧化二鋁含量等.式(8)中的ψ(x)選擇高斯核函數,核函數的寬度h=135,式(14)是凸優化函數,使用隨機梯度下降法計算最優解.在線檢測數據以分解爐溫度為例,采集1 700 組數據測試結果如圖14 所示,離線檢測數據以生料中三氧化二鋁含量為例,采集450 組數據測試結果如圖15 和圖16 所示.

圖14 表明,分解爐溫度在865?C 時,密度比為0.8,偏離密度比1,此值為異常值.

圖15 為采集的450 組正常數據和測試數據頻率直方圖,測試樣本中氧化鋁含量為3.75 時有4 組數據為異常數據;圖16 表明,當生料中三氧化二鋁含量為3.75 時,密度比估計值為0.81,偏離密度比估計值1.所以結合圖15 和圖16,3.75 為異常值.

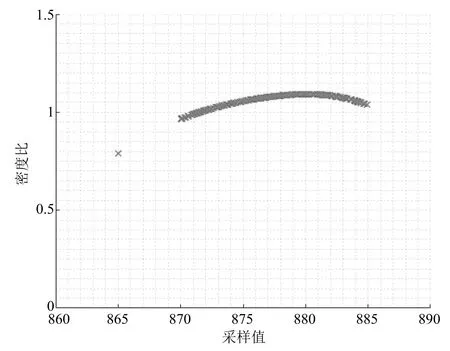
圖14 基于KL 散度密度比的分解爐溫度異常值檢測Fig.14 Abnormal value detection based on Kullback-Leibler divergence density ratio for calciner temperature

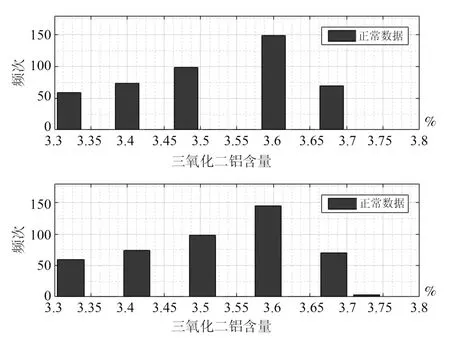
圖15 三氧化二鋁含量正常數據和測試數據Fig.15 Normal data and test data for Al2O3content

基于模糊模型的協調因子模塊,生料中4 種成分的設定值分別為:CCaSP(k)=36,CFeSP(k)=3.4,CSiSP(k)=13.5 及CAlSP(k)=3.55,模糊模型輸入因子n1=10,n2=5,n3=8 及n4=5,輸出因子m=10,l=1.

基于以上參數,生料分解率模型輸出值與離線檢測值如圖17 所示.采用均方根誤差(Root mean squared error,RMSE)衡量模型輸出值λ和離線檢測值λa之間的誤差,如式(39)所示.

其中,n代表采樣數,表4 為本文所提方法與LSSVM 和RFMPCA-LS-SVM 之間的對比.

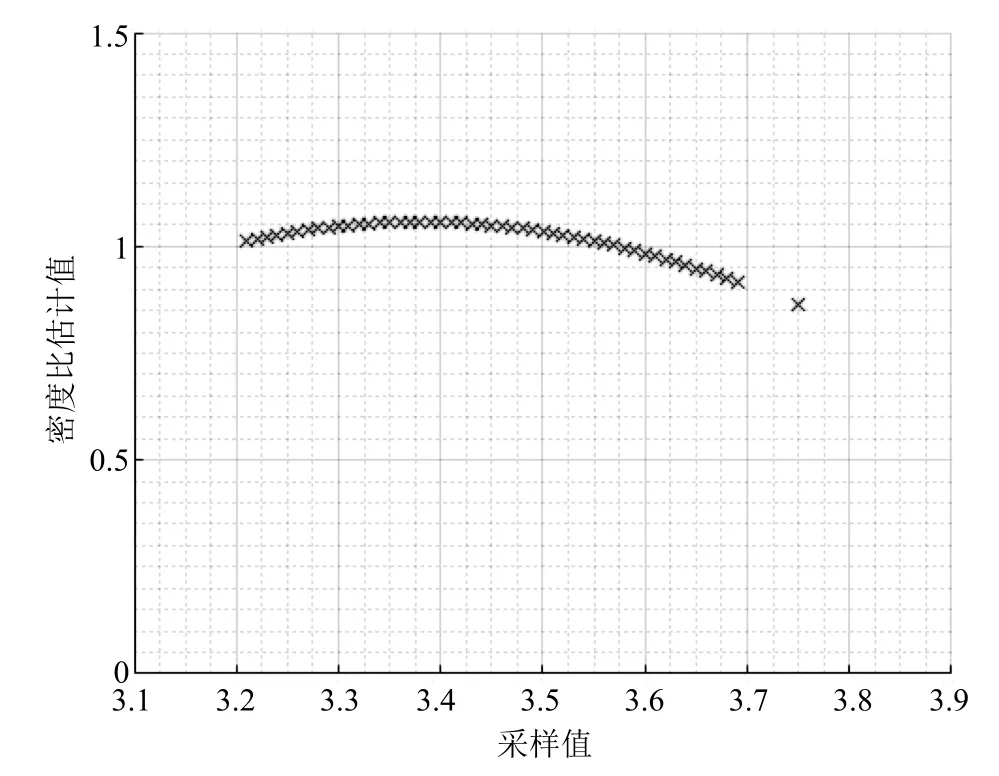
圖16 基于KL 散度密度比的三氧化二鋁含量異常值檢測Fig.16 Abnormal value detection based on Kullback-Leibler divergence density ratio for Al2O3content

圖17 生料分解率模型輸出值與離線檢測值曲線Fig.17 The curve of model output value and offline detection value for raw meal decomposition ratio

表4 本文所提方法與LS-SVM 和RFMPCA-LS-SVM 的RMSE 對比Table 4 The RMSE comparison among the method proposed and LS-SVM and RFMPCA-LS-SVM

表4 中,使用LS-SVM、RFMPCA-LS-SVM 和本文所提方法產生的RMSE 分別為1.1325、1.0235和1.0198.使用LS-SVM 方法誤差較大的原因是模型計算時沒有對采樣數據進行異常值處理,而RFMPCA-LS-SVM 方法使用了魯棒3σ進行異常值檢測,本文所提方法使用基于KL 散度密度比的異常值檢測方法,仿真實驗結果表明,本文所提方法優于LS-SVM 和RFMPCA-LS-SVM 方法.

圖18 生料分解過程Fig.18 The raw meal calcination process

4 工業應用

本文所提出的數據與模型驅動的水泥生料分解率軟測量模型已經成功應用于某水泥廠生料分解過程中.此算法的硬件平臺是西門子S7-400,軟件平臺是Step7 V5.4 與WinCC V6.2.

4.1 硬件平臺

生料分解過程如圖18 所示,其主控畫面如圖19所示.硬件平臺由PLC 控制系統、優化設定計算機、程師站和操作員站、電器及儀表、網絡和通訊系統組成,如圖20 所示.

在圖20 中,PLC 控制系統包括3 臺西門子S7-400 控制器構成的主站、輸入及輸出模塊、電源模塊及CP443-1 通訊模塊,各個主站通過Profibus-DP連接ET200M 從站.中控室設置優化設定計算機、工程師站和3 臺操作員站.

4.2 算法實現

生料分解過程中控室安裝3 臺操作員站和1 臺工程師站,其中工程師站除了裝有Step7 和WinCC軟件外,還安裝Visual C# 軟件,生料分解率軟測量模型算法在Visual C# 中編程,通過OPC 通訊實現,算法的流程圖如圖21 所示.

4.3 參數選擇

根據第2 節的數據與模型驅動的水泥生料分解率軟測量模型,模型參數如下所示.

1)基于KL 散度密度比的異常值檢測模塊:式(15)中的核函數的寬度h=135.

圖19 生料分解過程主控畫面Fig.19 The main picture of raw meal calcination process

圖20 系統硬件平臺Fig.20 The architecture of system hardware platform

2)基于模糊模型的協調因子模塊:參數選擇如表5 所示.

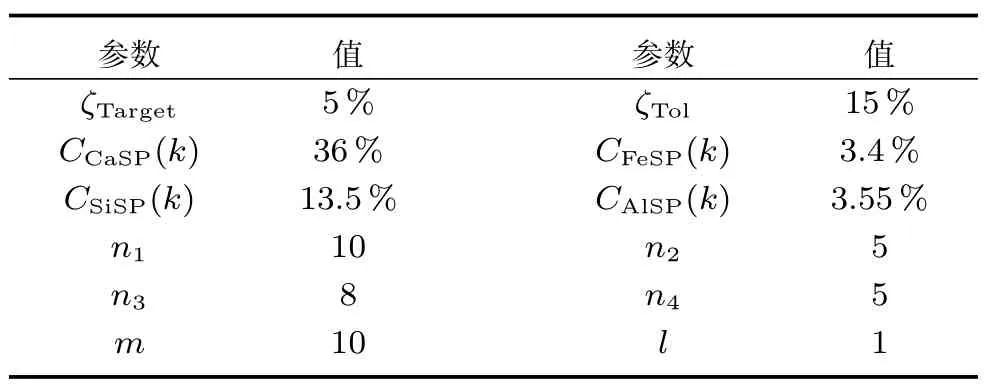
表5 基于模糊模型的協調因子參數選擇Table 5 Parameters selection based on fuzzy model

4.4 應用結果

將數據與模型驅動的水泥生料分解率軟測量模型應用于某水泥生料分解過程,在2018 年10 月28日從11:06 AM 至15:06 PM 時運行曲線如圖22～24 所示,曲線的橫坐標為時間軸,縱坐標為各變量的數值軸.

圖22 為基于模糊模型的協調因子運行曲線,在2018 年10 月28 日11:06 AM 至11:42 AM 時,生料中四種成分變化在正常工況范圍內,如表6 所示.此時,協調因子λ=0,基于機理的生料分解率模型被采用.在12:18 PM 至12:43 PM 時,隨著生料中CaO 含量由36.5% 增大到37.8%,協調因子λ由0.1 增大到0.4,采用基于機理和層級S 核函數的生料分解率模型.在13:30 PM 至13:42 PM 時,生料中Al2O3含量由3.7% 降低到3.3%,協調因子λ由0.4 降低到?0.2.

圖21 算法實現控制流程圖Fig.21 The flow chart of algorithm realization

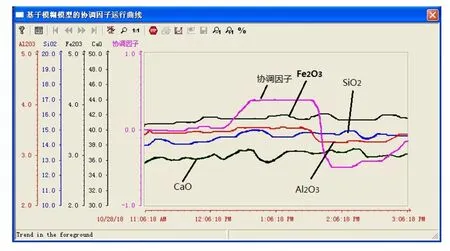
圖22 基于模糊模型的協調因子運行曲線Fig.22 The curve of coordination factor based on fuzzy model

圖23 生料分解率運行曲線Fig.23 The run curve of raw meal decomposition ratio

圖24 預熱器C5 下料管堵塞概率與生料分解率和預熱器C5 出口溫度之間的關系曲線Fig.24 The curve among blocking probability of preheater C5 tube and raw meal decomposition ratio and outlet temperature of preheater C5

表6 生料中4 種成分變化范圍Table 6 Range of four components in raw meal

圖23 為生料分解率運行曲線,結合圖22,在2018 年10 月28 日11:06 AM 至11:42 AM,生料分解率γ由90.2% 增大到95.8%.在12:02 PM至12:43 PM 時,生料分解率γ由95.8% 降低到92.1%.此時,從圖24 可知,預熱器C5 下料管堵塞概率達到10%.因此,結合圖22～24,需要根據生料中成分變化,及時調節入分解爐煤粉量,使生料分解率達到最佳值,進而提高臺時產能,降低煤耗.

4.5 結論

本文提出了數據與模型驅動的水泥生料分解率軟測量模型.解決了建模過程采樣數據異常值檢測及生料分解率實時在線檢測的難題,該模型能夠根據當前工況的變化確定模糊協調因子,進而得出機理與層級S 核函數加權的生料分解率軟測量模型,降低了預熱器C5 下料管堵塞概率.所提出的方法已經成功應用于某水泥廠水泥生料分解過程.下一步著重研究基于知識和數據驅動的水泥生料分解率軟測量建模.