基于高斯分布的密度誤差對航天器軌道的影響分析?

劉衛,劉四清,龔建村,王榮蘭

(1.中國科學院國家空間科學中心,北京100190；2.中國科學院微小衛星創新研究院,上海201210；3.中國科學院大學,北京100049)

1 引言

自1961年美國子午儀-4A衛星在軌爆炸以來，可觀測空間碎片數量出現大規模增長[1]。1978年1月，入軌僅3個月載有核反應堆的宇宙954衛星再入時，在加拿大上空失控，沿約1000km的區域釋放了約30kg核輻射物[2]。1996年7月，法國櫻桃衛星被1986年11月阿里安火箭爆炸的碎片撞擊損壞[3]；2009年在用衛星美國銥星33和俄羅斯宇宙2251發生碰撞，產生可追蹤碎片超過2000塊[4，5]；1989年3月的太陽大爆發造成了大量太空編目目標的丟失，2012年7月美國空間監視網 (SSN)更是創下目標丟失列表紀錄[6，7]，原因也正是太陽活動峰年的熱層大氣模式誤差。近年來空間目標頻繁發生在軌碰撞，隕落進入地球大氣燒毀，甚至砸至地面，對人類的空間資產和地面安全造成威脅。熱層密度預測值的不確定性造成的空間碎片的軌道衰減，對碰撞發生時間和位置的預測有很大影響[1]。碰撞預警計算中漏警、虛警時有發生，隕落預報中誤差較大等這些問題都是熱層大氣密度預測誤差直接或間接造成的。20世紀50年代末，第一顆人造衛星上天后觀測到大氣阻力對衛星軌道運動的影響。基于衛星軌道衰變數據，Jacchia等人在20世紀60～70年代開發出第一代通用經驗大氣模型，如HarrisPriester、Jacchia模型[8]。經過數十年發展，目前已有Jacchia、DTM和MSIS等系列熱層大氣密度模式，這些模式平均而言，均存在15%～20%的誤差，空間環境擾動期間誤差甚至超過100%[9，10]，無法滿足空間態勢感知等高精度的軍事需求。

Travis等人利用CHAMP和GRACE精密星歷(POE)估算大氣密度，評估大擾動期間的密度變化，發現使用POE推導密度與加速度計反演密度預測的軌道之間的誤差很小。因此Travis認為加速度計觀測到的熱層密度高頻變化項，對軌道分析應用都不重要[11]。大氣阻力可以從近地軌道衛星的軌道信息中推斷出來，為測量質量密度提供了一種直接的手段。CHEN等人基于半長軸的阻力攝動方程，使用CHAMP衛星反演密度，發現應用反演密度可以減少軌道預測誤差[12]。Rodney等人通過2003～2007年期間CHAMP衛星加速度計數據，驗證密度模型延時誤差的影響，并分析延遲對軌道預測結果的影響[13]。

在熱層大氣模型性能評測中，通常給出相對誤差標準差，如15%～20%，而忽略誤差均值問題。那么熱層大氣密度模式誤差的統計特性上是否為零均值，非零均值如何影響航天器軌道預報，標準差又是如何影響軌道預報的呢。典型熱層模式誤差及對軌道預報影響的相關文獻多見報道，但未見文獻給出上述問題答案。本文通過熱層模式誤差特性的統計和軌道預報數值試驗，將給出上述問題的答案。期待為熱層模式的軌道預報應用改進、建模指引方向。

2 模式誤差特性

從熱層大氣建模的角度來看，熱層模式不應存在系統性偏差，也就是相對誤差均值不為零的情況。由于空間環境變化極其復雜，累積的熱層密度探測資料在時間空間上存在不連續、分辨率低等情況，目前熱層大氣的部分變化機制仍不確定。目前的熱層大氣模式在不同空間環境下表現出差異化的系統偏差。

2.1 模式長期特性

熱層模式的長期特性是指大時間尺度 (太陽活動周)上表現出來的偏差、標準差等性質。

為定量評估動態改進前后模式性能，我們定義模式偏離實測的百分比，即相對誤差ε:

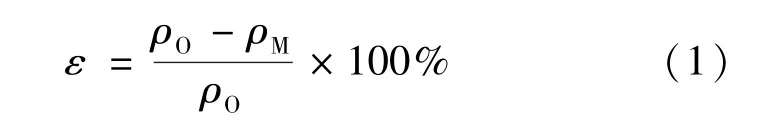
式中，ρO，ρM分別是密度實測值和模式值。

PARDINI等人通過分析四顆衛星半長軸衰減，評估了JR-71、 MSIS-90、 MSISE00、 GOST-2004、JB2006和JB2008六種大氣模式，指出由于建模時采用高度無關的固定值阻力系數，此六種大氣模式均高估500km以下大氣密度約7%～20%[14]。平均偏差最小的模式依次是 JB08、MSISE00和GOST-2004。同時給出了第23太陽活動周峰年各模式在不同高度的平均偏差，見表1。

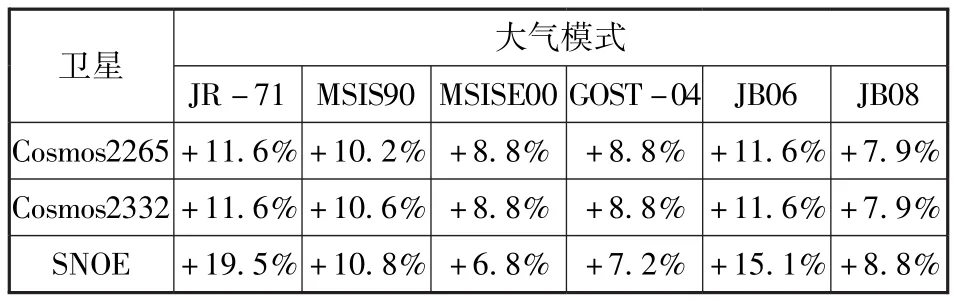
表1 各模式不同高度的平均偏差Tab.1 The mean bias of different models

劉衛等人基于CHAMP衛星2001年5月15日至2008年12月31日期間加速度計反演熱層大氣密度數據為基準，對JB2008和MSISE00兩模式誤差進行統計分析[15]，給出了 JB2008和MSISE00兩種模式在不同類型的空間環境下，相對誤差均值、標準差的特性，如表2所示。

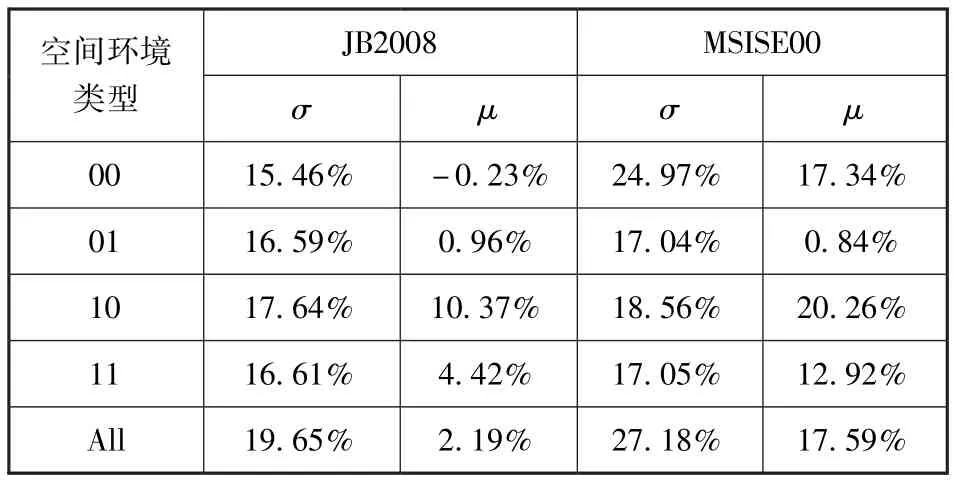
表2 兩大氣模式相對誤差均值與標準差@400kmTab.2 The mean relative error and standard deviation at 400km altitude

由上述統計分析表明，長期而言典型模式誤差均值仍不為零，并且在不同空間環境、高度表現也不同。

2.2 事件期間的模式特性

空間環境事件期間的模式特性是指小時間尺度 (幾天)上，發生空間環境擾動事件時，熱層大氣模式表現出的誤差特性，包括誤差均值和標準差。圖1是基于CHAMP加速度計反演熱層密度，以日為區間單位統計給出的MSISE00模式的相對誤差均值和標準差隨太陽活動指數F10.7和地磁活動指數Ap的變化情況。圖中可見MSISE00模式相對誤差均值μ和標準差σ，隨空間環境變化，幾次磁暴均存在μ和σ陡增，μ達到100%，σ甚至可以達到300%。

圖2給出2003年10月31日磁暴事件期間JB2008和MSISE00模式相對誤差分布。圖2可見，JB2008相對MSISE00模式誤差分布更集中，數據統計兩模式在該磁暴事件期間的相對誤差均值分別為48%和75%。

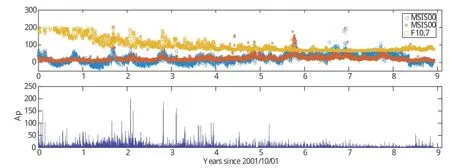
圖1 MSISE00模式相對誤差均值和標準差隨空間環境的變化Fig.1 Variation of mean and standard deviation of MSISE00 model error with space environment

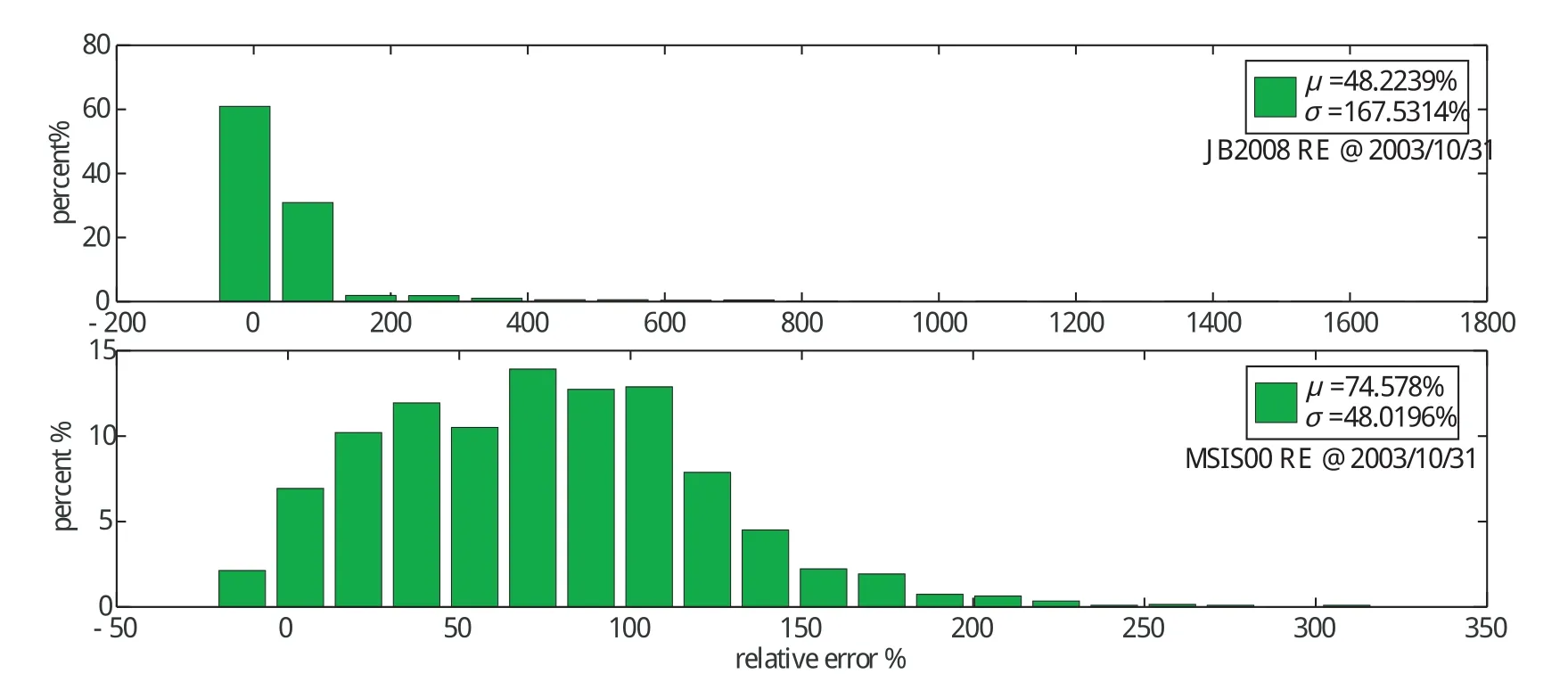
圖2 2003年10月31日磁暴事件期間JB2008和MSISE00模式相對誤差分布圖Fig.2 Relativeerror distribution of JB2008 and MSISE00 models during the 2003/10/31 event

由上述統計可見，無論是熱層模式的長期特性還是空間環境事件期間的模式特性，熱層大氣模式誤差均值和標準差都不為零，空間環境事件期間表現更加明顯。

3 軌道預報影響統計

3.1 軌道預報

CHAMP衛星的快速科學軌道 (Rapid Science Orbit，RSO)數據具有較好的連續性，且軌道位置精度優于10cm[12]。我們以CHAMP衛星采樣間隔30s的RSO星歷數據為參考軌道，對軌道預報結果進行比較分析，軌道預報中的主要模型和參量:

(1)99×99階地球引力場模型GGM05C；

(2)30×30階TOPEX 4.0海潮模型；

(3)CHAMP加速度計反演大氣密度；

(4)坐標、時間及天文常數系統采用IERS(2010)標準；

(5)日、月引力攝動；

(6)太陽光壓，固體潮攝動。

3.2 高斯分布誤差

符合高斯分布誤差產生同樣是模式誤差如何影響軌道分析的關鍵。我們的高斯分布誤差產生是基于兩個均勻分布隨機變量的組合獲取的，具體理論如下。如果x1，x2… 是具有聯合概率分布p(x1，x2…)dx1dx2…的隨機偏離，并且如果y1，y2…每個都是所有x的函數，則y的聯合概率分布為:

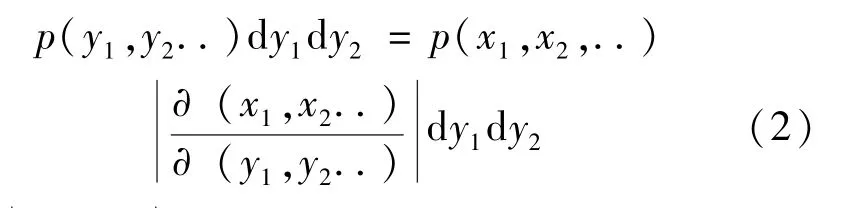
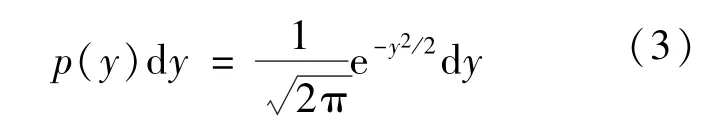
考慮 (0，1)內兩個一致偏離x1，x2與兩個變量y1，y2之間的變換:

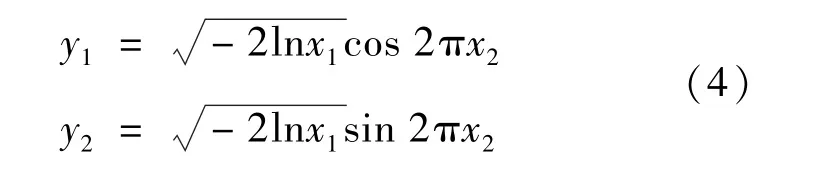
等價地可寫成:

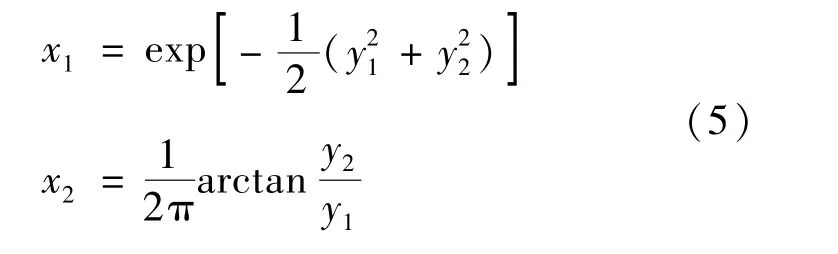
雅克比行列式可以如下計算[16]:

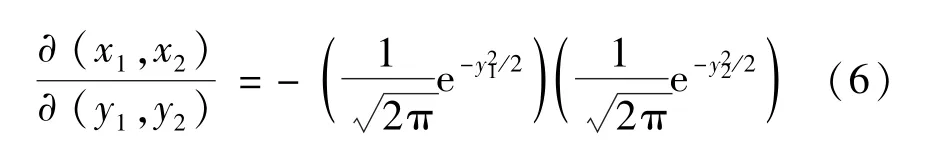
上式是y1函數與y2函數的乘積，都獨立服從正態分布。這是符合 (0，1)高斯分布的隨機變量y，那么任意(μ，σ)高斯分布的隨機變量y′可如下獲取:

圖3是實際仿真計算中產生的高斯分布隨機誤差，圖3中 (a)、(b)、(c)設定的均值和標準差分別是:30%、100%；30%、50%；10%、80%；實際產生的誤差均值和標準差分別是:29.08%、98.68%；29.54%、49.34%；10.74%、78.94%，符合要求。

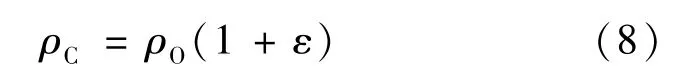
式中，ρC，ρO分別是計算中使用的密度值和密度實測值。高斯分布隨機誤差由上述公式產生后，按照式 (8)計算熱層密度，進行軌道預報并統計預報誤差情況。

4 結果分析

前節模式特性分析可見，空間環境事件期間熱層大氣模式存在較大的誤差均值和標準差。因此空間環境擾動期的航天器軌道預報是航天工程應用的痛點問題。我們以3h值ap≥236為條件篩選出2001～2010年期間，具有CHAMP軌道數據的16個磁暴事件，見表3。施加符合不同均值和標準差的高斯分布熱層密度誤差，分析軌道預報誤差。發現16個磁暴事件中，在相同誤差參數下，軌道預報特性相似，下面選取幾個典型事例進行展示分析。

4.1 相同均值的比較

以2003年10月29日磁暴事件為例，在軌道預報中，分別施加誤差均值μ=0%，-10%，-30%，10%，30%，每種誤差均值下又結合不同的誤差標準差σ=0%，10%，30%，50%，80%，100%進行軌道預報誤差統計。圖4展示的是相對誤差均值相同，不同標準差下軌道預報誤差。圖中相同均值下，軌道預報誤差對標準差的變化不敏感，隨標準差的增大有所增加。整體上軌道預報誤差隨誤差均值絕對值增加而迅速增大，均值的正負決定預報偏差的方向。

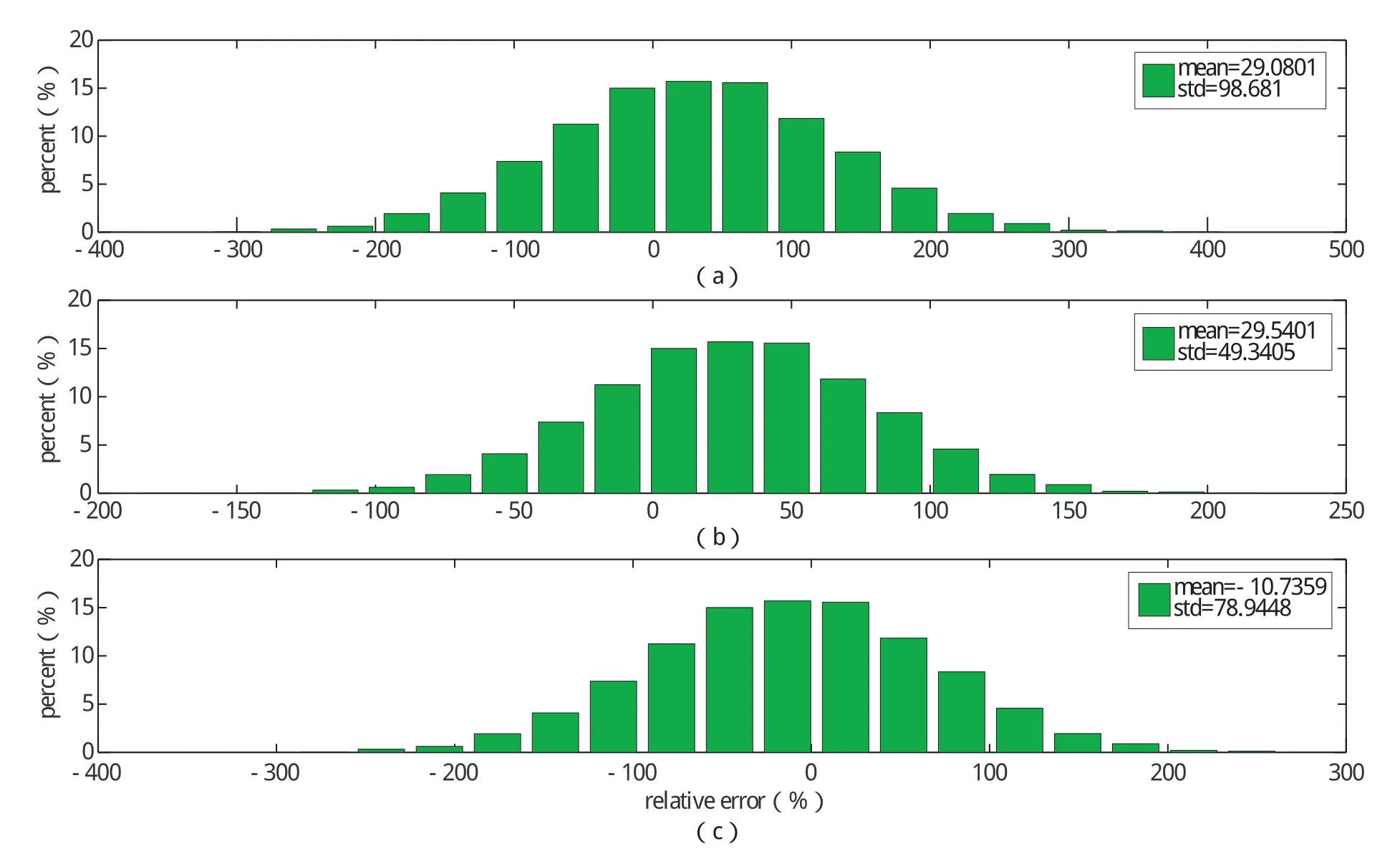
圖3 實際產生的高斯隨機誤差分布圖Fig.3 Actual Gauss random error distribution

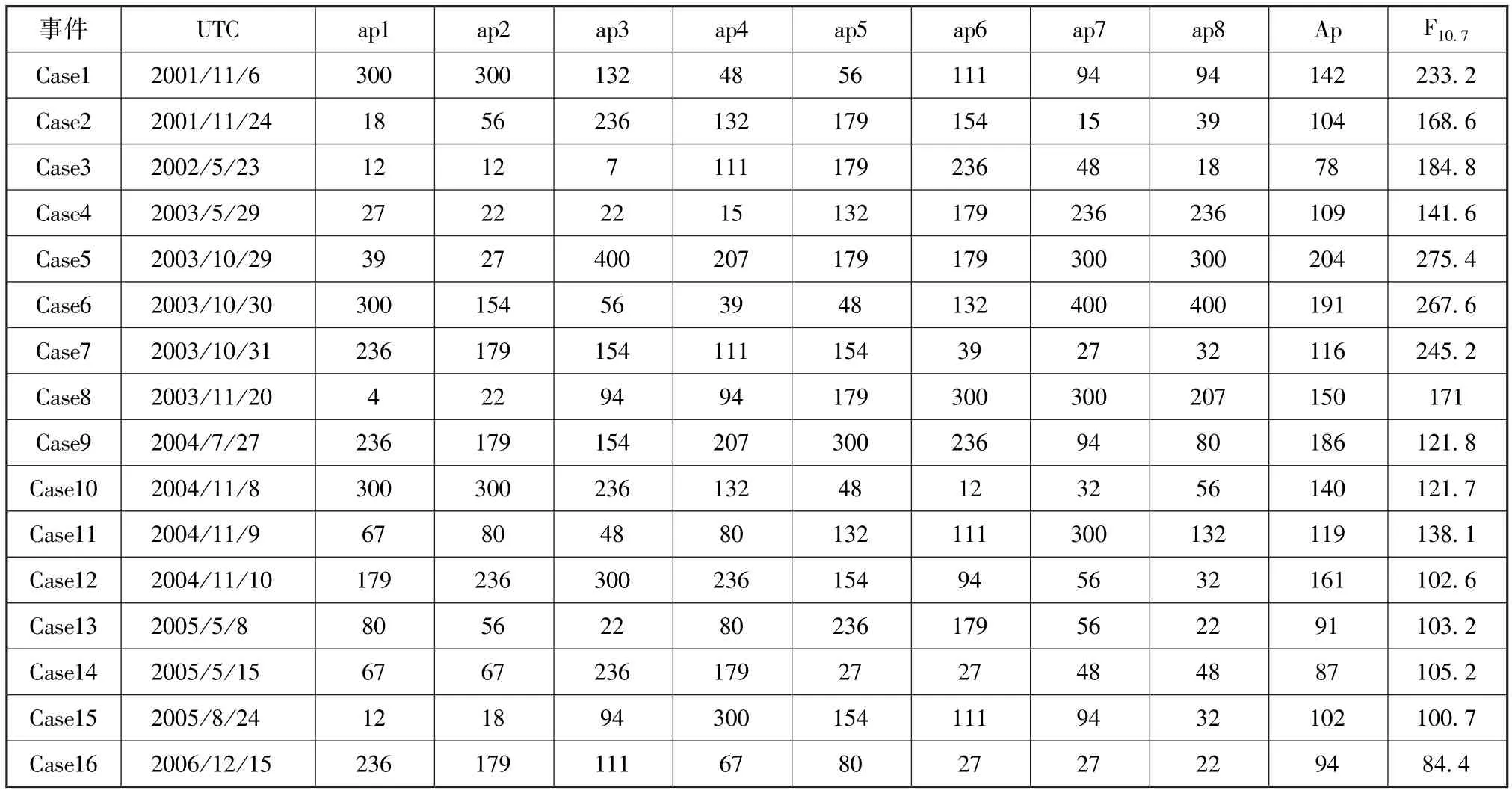
表3 篩選的空間環境事件信息Tab.3 The selected space environmental event information

圖4 不同相對誤差標準差下軌道預報誤差 (均值0%，-10%，-30%)Fig.4 Orbit prediction errors(mean values 0%，-10%，-30%，10% and 30%)under different relative error standard deviations

4.2 相同標準差比較

以2003年10月30日磁暴事件為例，在軌道預報中，分別施加誤差標準差σ=10%，30%，50%，80%，100%，每種相對誤差標準差又結合不同的均值μ=0%，-10%，-30%，10%，30%進行軌道預報誤差統計。圖5、圖6展示的是相對誤差標準差相同，不同均值下軌道預報誤差。與上節結果一致，軌道預報誤差主要取決于誤差均值絕對值，對標準差的變化不敏感。誤差均值的正負決定預報偏差的方向，同時證明軌道預報結果對熱層小尺度的變化不敏感，熱層密度誤差可以通過平均進行補償。

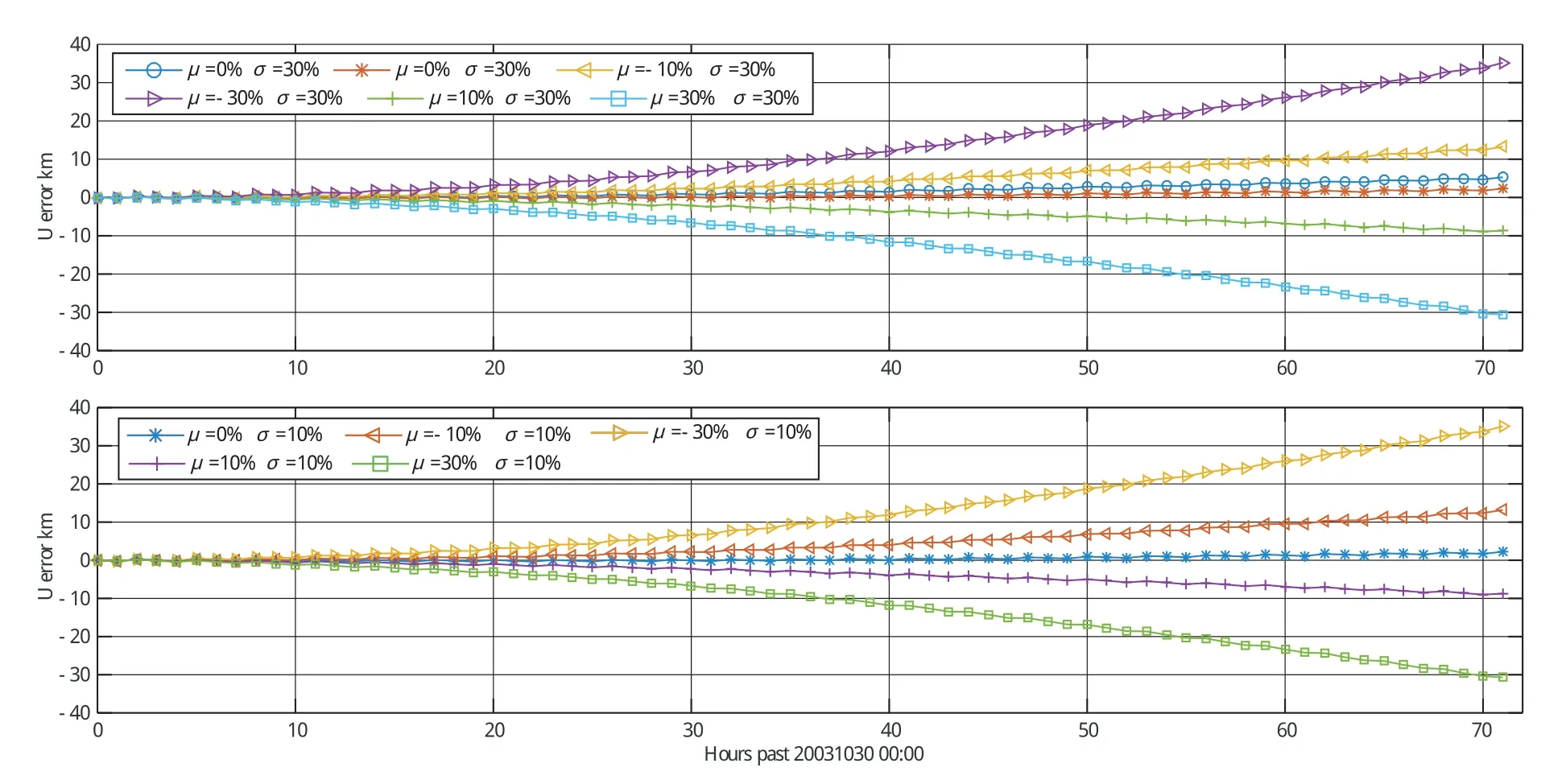
圖5 不同相對誤差均值下軌道預報誤差 (標準差10%和30%)Fig.5 Orbit prediction errors(standard deviations 10% and 30%)under different relative error mean values

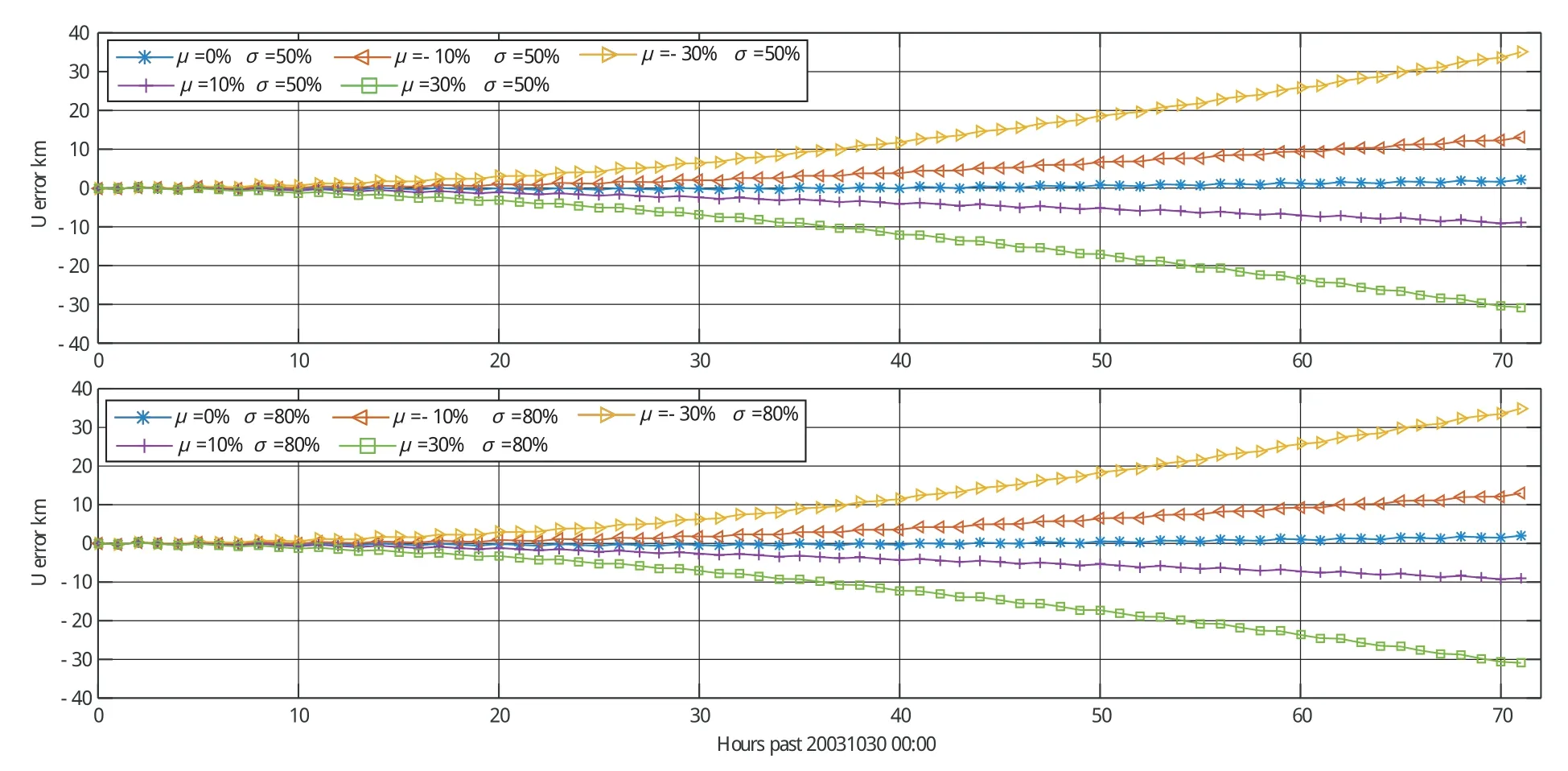
圖6 不同相對誤差均值下軌道預報誤差 (標準差50%和80%)Fig.6 Orbit prediction errors(standard deviations 50% and 80%)under different relative error mean values

5 結論

本文介紹基于高斯分布的密度誤差對航天器軌道的影響分析的必要性，統計典型熱層模式誤差的長期特性和空間環境事件期間模式誤差特性，給出航天器軌道預報中引入高斯分布熱層密度相對誤差的方法，并進行驗證。篩選出2001～2010年期間，具有CHAMP軌道數據的16個磁暴事件，施加不同均值和標準差的高斯分布熱層密度誤差，分析軌道預報誤差。得到的主要結論如下:

(1)熱層大氣模式存在非零均值誤差，且該誤差隨空間環境而變化；

(2)典型熱層模式誤差均值和標準差，在空間環境擾動期最大可超過100%；

(3)軌道預報誤差主要取決于熱層模式誤差均值的絕對值，對誤差標準差不敏感，誤差均值的正負決定預報偏差的方向；

(4)軌道預報結果對熱層小尺度的變化不敏感，熱層密度誤差可以通過平均進行補償。

期望本文對熱層大氣模式改進、建模具有方向指引意義。