工業(yè)機(jī)器人工作空間求解及逆運(yùn)動(dòng)學(xué)唯一解的確定*

劉曰濤，沈?qū)毭瘢瑮?林，楊正嬌

(山東理工大學(xué) 機(jī)械工程學(xué)院，山東 淄博 255000)

0 引言

機(jī)器人的工作空間定義為，不同關(guān)節(jié)運(yùn)動(dòng)所達(dá)到的末端執(zhí)行器的所有位置的集合，該集合稱(chēng)為可達(dá)工作空間[1]。機(jī)器人的工作空間是研究設(shè)計(jì)機(jī)器人以及機(jī)器人應(yīng)用過(guò)程中需要考慮的一個(gè)重要的問(wèn)題。

目前用于研究機(jī)器人工作空間的算法主要有：幾何繪圖法、解析法以及數(shù)值法[2-10]，以上三種算法各有其優(yōu)勢(shì)。但是通過(guò)對(duì)現(xiàn)有機(jī)器人工作空間的求解算法對(duì)比研究發(fā)現(xiàn)，現(xiàn)有的關(guān)于機(jī)器人工作空間的算法大多太過(guò)于復(fù)雜，雖具有一定的研究意義，但實(shí)用性不強(qiáng)。本文基于MATLAB依據(jù)機(jī)器人工作空間的最基本算法對(duì)機(jī)器人結(jié)構(gòu)進(jìn)行簡(jiǎn)化，得出機(jī)器人工作空間的曲線(xiàn)圖，與繪圖法得出的機(jī)器人工作空間一致，由此證明了本算法的可行性。

同時(shí)本文還對(duì)機(jī)器人逆運(yùn)動(dòng)學(xué)進(jìn)行了計(jì)算和分析，并確定了機(jī)器人逆運(yùn)動(dòng)學(xué)唯一解。機(jī)器人逆運(yùn)動(dòng)學(xué)就是通過(guò)已知機(jī)器人末端的位置及姿態(tài)，計(jì)算所對(duì)應(yīng)的全部關(guān)節(jié)的變量，機(jī)器人逆運(yùn)動(dòng)學(xué)是機(jī)器人運(yùn)動(dòng)規(guī)劃和軌跡控制的基礎(chǔ)[11]。對(duì)于機(jī)器人逆運(yùn)動(dòng)學(xué)解的計(jì)算方法有很多，包括Paul提出的反變換法[12],Lee和Ziegler的幾何法[13]，Pieper的方法[14]等。機(jī)器人正向運(yùn)動(dòng)學(xué)是給定各個(gè)關(guān)節(jié)變量之后，機(jī)器人末端位置和姿態(tài)是唯一確定的，而逆運(yùn)動(dòng)學(xué)一般具有多重解或無(wú)解，因此當(dāng)出現(xiàn)多重解的情況下對(duì)于唯一解的確定就尤為重要。

本文采用的是比較普遍的反變換法求解，之后再通過(guò)篩選和條件限制確定唯一解。

1 機(jī)器人工作空間的計(jì)算

1.1 工作空間計(jì)算過(guò)程

本文以普通的6軸串聯(lián)機(jī)器人為研究對(duì)象，機(jī)器人各個(gè)關(guān)節(jié)對(duì)其末端的位置和姿態(tài)的作用不同，前3個(gè)軸主要是實(shí)現(xiàn)末端的位置要求，被稱(chēng)為位置結(jié)構(gòu)；后3個(gè)軸主要是實(shí)現(xiàn)末端姿態(tài)的要求，被稱(chēng)為姿態(tài)結(jié)構(gòu)；機(jī)器人的工作空間的大小主要受位置結(jié)構(gòu)的影響[15]。機(jī)器人工作空間設(shè)計(jì)時(shí)也是以第1、第2、第3軸及其所對(duì)應(yīng)的臂長(zhǎng)進(jìn)行設(shè)計(jì)。對(duì)機(jī)器人工作空間計(jì)算時(shí)只需考慮機(jī)器人的前3個(gè)軸即可，為了提高機(jī)器人工作空間的直觀性，甚至可以只計(jì)算機(jī)器人的第2、第3軸及其所對(duì)應(yīng)的臂長(zhǎng)，這樣可以大大減小機(jī)器人工作空間的計(jì)算量提升機(jī)器人工作空間的求解速度。

本文所研究的6自由度工業(yè)機(jī)器人結(jié)構(gòu)簡(jiǎn)圖如圖1所示。

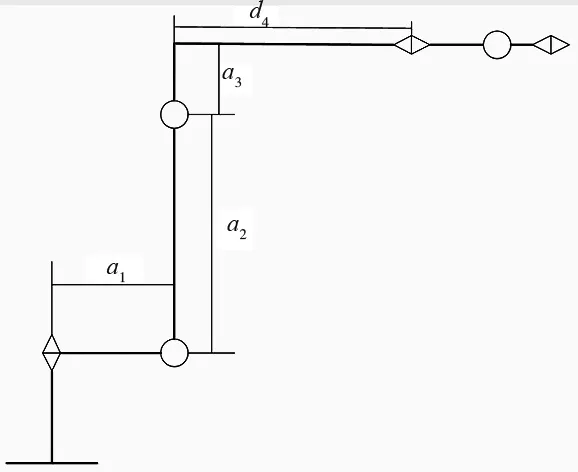
圖1 機(jī)器人結(jié)構(gòu)簡(jiǎn)圖

根據(jù)D-H算法給每一個(gè)關(guān)節(jié)賦予一個(gè)坐標(biāo)建立參數(shù)表，如表1所示。

表1 D-H參數(shù)表

依據(jù)表1建立機(jī)器人D-H算法的齊次變換矩陣為：

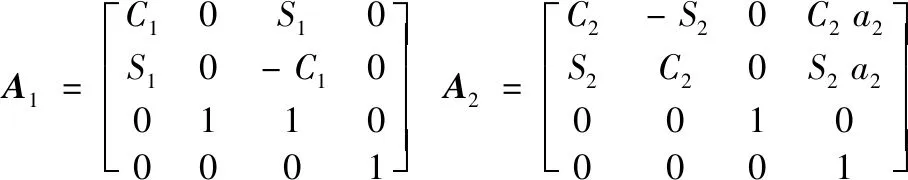
(1)

(2)

式中，Ci代表cosθi，Si代表sinθi。

式(1)、式(2)是以坐標(biāo)系前置根據(jù)機(jī)器人參數(shù)建立的6自由度工業(yè)機(jī)器人數(shù)學(xué)模型，本文工作空間的計(jì)算主要是依靠坐標(biāo)系后置所建立的數(shù)學(xué)模型進(jìn)行計(jì)算分析。

由于本文求解的機(jī)器人工作空間是其剖截面圖，即不考慮第一軸；在對(duì)機(jī)器人可達(dá)工作空間進(jìn)行分析時(shí)不考慮第4、5、6軸姿態(tài)的條件，所以最終只考慮第2軸和第3軸及其所對(duì)應(yīng)的大臂及小臂4個(gè)條件因素。

3T2=A2×A3=

(3)

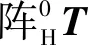
Px=a3(C2C3﹣S2S3)﹢a2C2

(4)

Py=a3(S2C3﹢C2S3)﹢a2S2

(5)

Pz=0

(6)

因?yàn)楸疚闹豢紤]了2軸和3軸，所以得出的是機(jī)器人工作空間的剖截面，故Pz=0。

根據(jù)機(jī)器人的結(jié)構(gòu)特點(diǎn)和運(yùn)動(dòng)特性，存在如下條件約束：

(1)各驅(qū)動(dòng)副轉(zhuǎn)角范圍。由于受到機(jī)器人機(jī)械臂上各零部件的影響和限制，機(jī)器人的大部分關(guān)節(jié)都有自己的轉(zhuǎn)動(dòng)范圍，很難實(shí)現(xiàn)全周轉(zhuǎn)動(dòng)。通過(guò)了解現(xiàn)有的6自由度機(jī)器人確定第2第3軸的轉(zhuǎn)角范圍如表2所示。

(2)臂長(zhǎng)。機(jī)器人的臂長(zhǎng)越長(zhǎng)其工作空間越大，但是為了適應(yīng)不同的工作環(huán)境，需要設(shè)計(jì)不同臂長(zhǎng)的機(jī)器人。

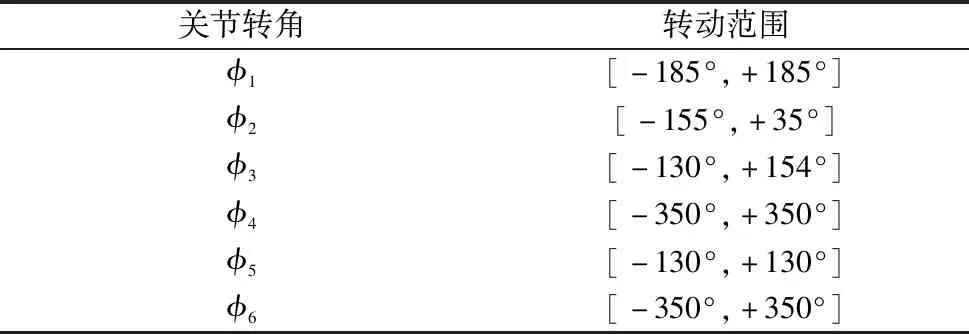
表2 機(jī)器人第2、3軸的轉(zhuǎn)角范圍

1.2 工作空間仿真與分析

用上述方法求(Px，Py)關(guān)于關(guān)節(jié)轉(zhuǎn)角在φ2、φ3轉(zhuǎn)動(dòng)范圍內(nèi)所有點(diǎn)的集合，得到的仿真結(jié)果如圖2所示。

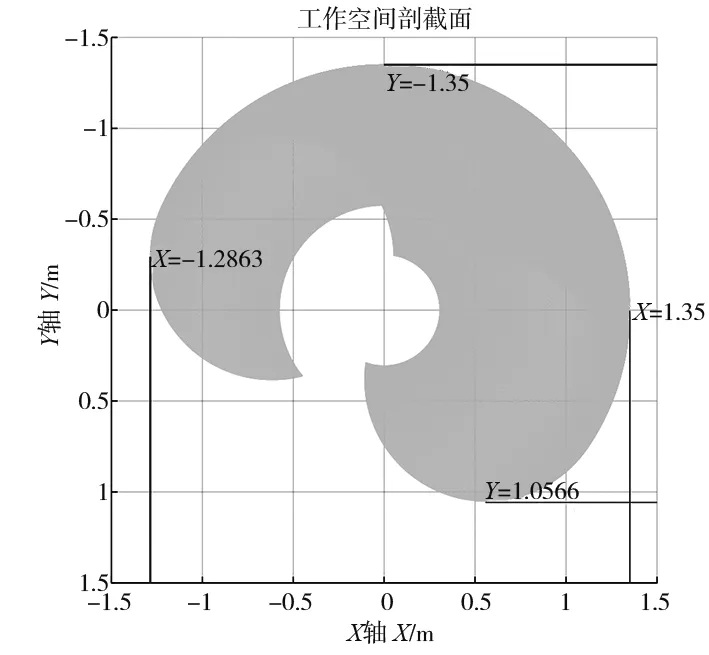
圖2 基于MATLAB生成的機(jī)器人工作空間圖

圖2是用本算法基于MATLAB生成的機(jī)器人工作空間圖，圖3是KUKA官方給出的機(jī)器人工作空間圖。為了使本算法生成的工作空間圖更具參考性和實(shí)用性，其參數(shù)和圖3所示的機(jī)器人工作空間參數(shù)相同，是實(shí)驗(yàn)室現(xiàn)有的一臺(tái)KUKA KR16型號(hào)機(jī)器人的參數(shù)。通過(guò)MATLAB生成的機(jī)器人工作空間圖在X軸方向的尺寸為2636.3mm，在Y軸方向的尺寸為2406.6mm；而庫(kù)卡官方給出的機(jī)器人工作空間圖在X軸方向的尺寸為2638mm，在Y軸方向的尺寸為2412mm，兩者在X軸方向上相差1.7mm，在Y軸方向上相差5.4mm，因?yàn)樵趯?duì)工作空間具體計(jì)算時(shí)，具體的參數(shù)和KUKA內(nèi)部的參數(shù)存在一定的誤差，并且KUKA官方承認(rèn)所給的工作空間參考圖外觀尺寸并不是一個(gè)精確尺寸，由此可以確定通過(guò)此方法得出的機(jī)器人工作空間圖和繪圖法得出的機(jī)器人工作空間的剖截面圖基本相同。同時(shí)證明了本算法對(duì)于機(jī)器人工作空間的計(jì)算以及描述具有重要參考意義。

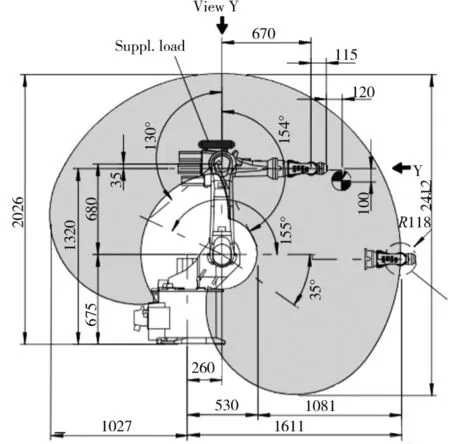
圖3 KUKA給出的機(jī)器人工作空間圖

2 機(jī)器人逆運(yùn)動(dòng)學(xué)解

2.1 機(jī)器人逆運(yùn)動(dòng)學(xué)解的計(jì)算

機(jī)器人逆運(yùn)動(dòng)學(xué)解對(duì)于機(jī)器人的重要性不言而喻，只有能夠計(jì)算出機(jī)器人逆運(yùn)動(dòng)學(xué)解才能確定機(jī)器人每個(gè)軸對(duì)應(yīng)的角度，進(jìn)而使機(jī)器人到達(dá)期望的位置及姿態(tài)。對(duì)于機(jī)器人逆運(yùn)動(dòng)學(xué)解已經(jīng)有比較成熟的算法，對(duì)于多個(gè)逆運(yùn)動(dòng)學(xué)解中唯一解的確定很少有文獻(xiàn)給出明確的方法，本文提供一種對(duì)于6自由度工業(yè)機(jī)器人唯一解確定的方法。

首先，需要確定機(jī)器人的結(jié)構(gòu)，根據(jù)機(jī)器人的結(jié)構(gòu)按照D-H算法建立數(shù)學(xué)模型。為了便于后期的分析對(duì)比，同時(shí)也使得所建立的模型更加接近實(shí)際，本文按照實(shí)驗(yàn)室里一臺(tái)現(xiàn)有的KUKA KR60-3型號(hào)的機(jī)器人建立數(shù)學(xué)模型。

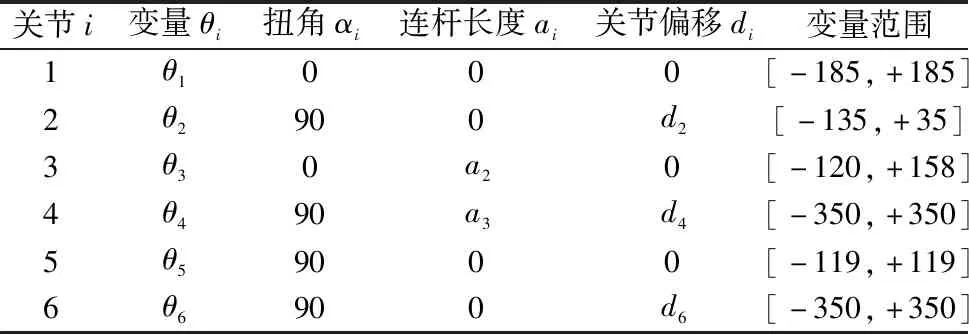
表3 機(jī)器人參數(shù)

本文數(shù)學(xué)模型的建立和式(1)數(shù)學(xué)模型的建立不同，為了對(duì)機(jī)器人逆運(yùn)動(dòng)學(xué)解的計(jì)算更加簡(jiǎn)便而采用了坐標(biāo)系前置，于是有：

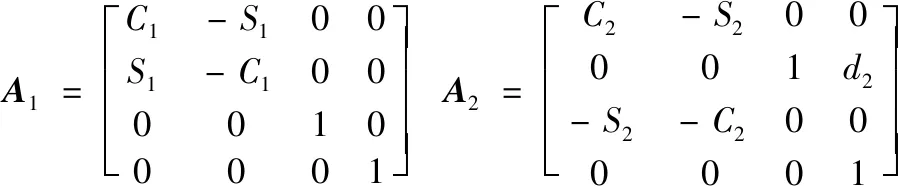
(12)

A=A1×A2×A3×A4×A5×A6

(13)

(14)

對(duì)于機(jī)器人逆運(yùn)動(dòng)學(xué)求解，根據(jù)式(13)進(jìn)行計(jì)算，因?yàn)槭?13)左側(cè)矩陣各元素已知，即式(14)矩陣A中所有元素是已知的，而右側(cè)的6個(gè)矩陣未知，Paul等人在進(jìn)行反變換計(jì)算時(shí)是用未知的逆變換依次左乘式(13)的矩陣方程，把關(guān)節(jié)變量分離出來(lái)，然后求解未知變量[11]。

對(duì)于具體的機(jī)器人逆運(yùn)動(dòng)學(xué)解的過(guò)程這里不再詳細(xì)描述，只介紹一下求逆解的步驟及結(jié)果：

(1)求解第一軸的反解。

用A1的逆矩陣左乘式(13)，經(jīng)過(guò)整理以及三角代換后可得出θ1。

(15)

由于公式里存在正負(fù)號(hào)，所以一軸有兩個(gè)解。

(2)求解第3軸的反解。

直接求解θ2因?yàn)閰?shù)不夠無(wú)法直接求出，所以先求解θ3(求解θ3的參數(shù)是足夠的，可以直接求出)，之后求解θ23即θ2+θ3的和，然后減θ3，最后得出θ2的具體解。

(16)

其中，

(17)

同樣三軸也有兩個(gè)解。

(3)求解第二軸的反解。

如上所述，這里首先求解θ23，然后減θ3，最后得出θ2的具體解。

θ23=θ2+θ3=atan2[-(a3+a2c3)pz+(c1px+s1py)
(a2s3-d4),(-d4+a2s3)pz+(c1px+s1py)(a2c3+a3)]

(18)

θ2=θ23-θ3

(19)

因?yàn)棣?和θ3各有兩個(gè)解，有4種可能的組合，所以可以得到θ2的4種可能的解。

(4)求解第4軸的反解，在5軸角度不為0的前提下可解出4軸的唯一解(當(dāng)五軸為0時(shí)即為奇異形位)。

通過(guò)上面對(duì)式(13)的依次左乘，θ4可以通過(guò)被左乘整理后的式(13)左右兩側(cè)參數(shù)的對(duì)應(yīng)直接求出。

θ4=atan2(-axs1+ayc1,-axc1c23-ayc1c23+azs23)

(20)

(5)求解5軸的反解

θ5=atan2(s5,c5)

(21)

(6)求解6軸的反解

θ6=atan2(s6,c6)

(22)

在求解第4、5、6軸的反解時(shí)，第5軸在取得唯一解的同時(shí)也可取當(dāng)前解的負(fù)數(shù)解，而同時(shí)第4軸和第6軸在當(dāng)前解的前提下可以加180°，可取得相同姿態(tài)，所以一共有8個(gè)解。同時(shí)如果第4軸和第6軸的轉(zhuǎn)動(dòng)范圍可達(dá)到將近±360°，則在最終姿態(tài)解上會(huì)更多，但是這并不意味著6自由度工業(yè)機(jī)器人的解已經(jīng)超過(guò)了8個(gè)，而是多余的解是在我們限定的周期以外。

此時(shí)一個(gè)6軸工業(yè)機(jī)器人的6個(gè)軸的解已經(jīng)全部計(jì)算完成，并且已經(jīng)確定共有8個(gè)解，下一步需要對(duì)這8個(gè)解進(jìn)行篩選以確定唯一解。

2.2 唯一解的確定

確定了機(jī)器人所有解以后，通過(guò)確定空間內(nèi)兩個(gè)不同點(diǎn)，即機(jī)器人從位置1到達(dá)位置2。本文可以對(duì)比大部分機(jī)器人在執(zhí)行所有的程序之前為什么必須確定Home點(diǎn)，因?yàn)镠ome點(diǎn)是所有程序開(kāi)始執(zhí)行的第一個(gè)位置，也就確定了最原始位置的唯一解。為了對(duì)原理理解的更加簡(jiǎn)單清晰，這里假設(shè)Home點(diǎn)即為位置1，由此確定了位置1的唯一解。

對(duì)位置2求反解，前面已經(jīng)確定位置2會(huì)有8個(gè)解，但是這8個(gè)解中首先可以排除4個(gè)解，即第一軸中在確定一個(gè)解以后，第二個(gè)解是首先確定的解加180°(只有當(dāng)關(guān)節(jié)偏移為0時(shí)才是180°)。剩余的4個(gè)解可以繼續(xù)排除2個(gè)，即通過(guò)第2軸和第3軸轉(zhuǎn)動(dòng)范圍進(jìn)行排除，因?yàn)闄C(jī)器人受機(jī)械的限制不可能每個(gè)軸都可以旋轉(zhuǎn)360°，由此可以排除第2、3軸中轉(zhuǎn)動(dòng)角度較大的解。

最終只剩下兩個(gè)解，而這兩個(gè)解是第5軸取正負(fù)所取得第4軸和第6軸同原解相差180°的兩組不同的解，由于之前確定了位置一的唯一解，由此判斷在運(yùn)動(dòng)過(guò)程中使得第6軸轉(zhuǎn)動(dòng)最小的解即為最優(yōu)解，由此確定了6自由度工業(yè)機(jī)器人逆運(yùn)動(dòng)學(xué)的唯一解(選擇第6軸轉(zhuǎn)動(dòng)最小是因?yàn)榭紤]結(jié)合實(shí)際情況，當(dāng)機(jī)器人末端到達(dá)下一個(gè)位置姿態(tài)時(shí)，使得機(jī)器人末端的動(dòng)作盡量的小)。

以上所有分析均為機(jī)器人工作位置二不在奇異形位，第4和第6軸未超出其轉(zhuǎn)動(dòng)范圍的前提下。當(dāng)?shù)?軸和第6軸有一個(gè)軸超出其轉(zhuǎn)動(dòng)范圍時(shí)，可以選擇使第5軸取原解的負(fù)數(shù)，同時(shí)判斷第4軸和第6軸是正向超出其轉(zhuǎn)動(dòng)范圍還是負(fù)向超出其轉(zhuǎn)動(dòng)范圍，由此選擇在原來(lái)的基礎(chǔ)上加或者減180°。

本文按照實(shí)驗(yàn)室現(xiàn)有的一臺(tái)KUKA KR60-3型號(hào)的機(jī)器人參數(shù)建立模型，以便于能夠和現(xiàn)實(shí)情況進(jìn)行對(duì)比，即a1=350mm、a2=850mm、a3=145mm、d2=0(指的是二軸的關(guān)節(jié)偏移和三軸的關(guān)節(jié)偏移總和為0)、d4=820mm。本算法通過(guò)MATLAB仿真和KUKA實(shí)際運(yùn)動(dòng)走相同的一段路徑，通過(guò)KUKA研發(fā)的一款名為mxAutomation軟件對(duì)KUKA所經(jīng)過(guò)的路徑的點(diǎn)進(jìn)行記錄，之后同樣通過(guò)MATLAB生成路徑曲線(xiàn)。

圖5是通過(guò)本算法對(duì)機(jī)器人行走的一段路徑的仿真曲線(xiàn)和通過(guò)記錄KUKA行走的一段路徑的點(diǎn)之后仿真出的路徑曲線(xiàn)，兩者起點(diǎn)和終點(diǎn)坐標(biāo)完全相同。

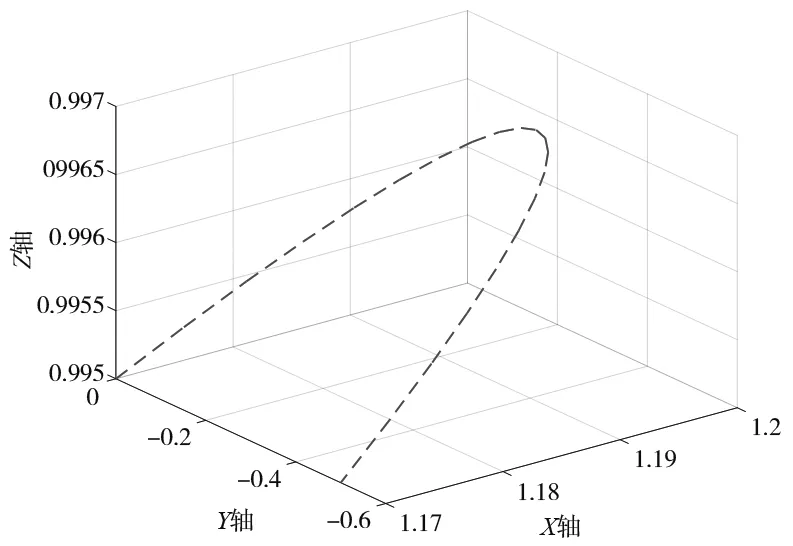
(a) 沿Y軸方向MATLAB仿真圖

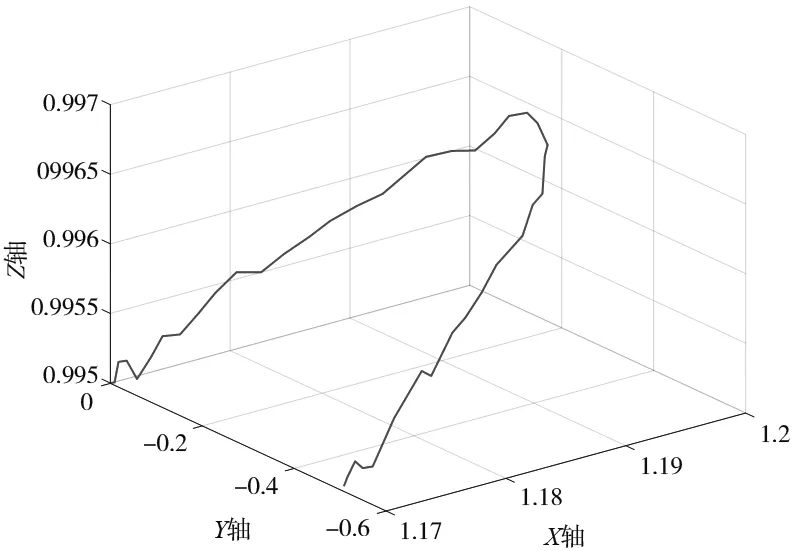
(b) 沿Y軸方向KUKA實(shí)際路徑圖

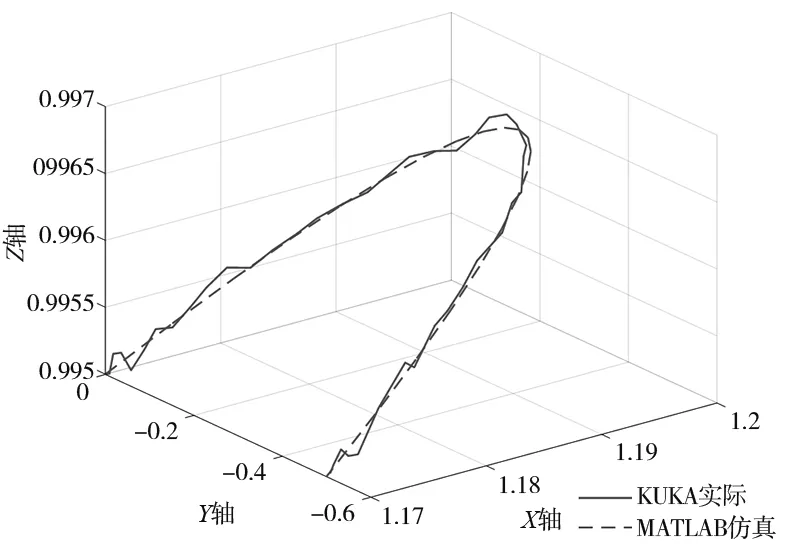
(c) Y軸方向下仿真與實(shí)際路徑對(duì)比圖

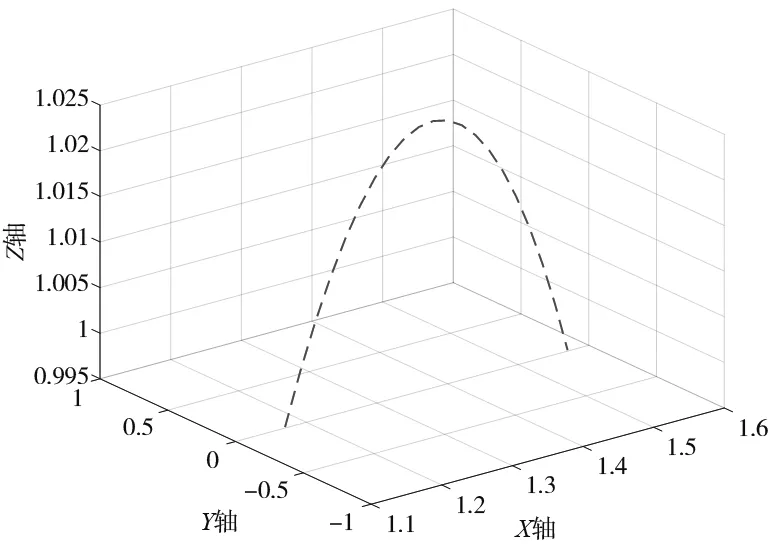
(d) 沿X軸方向MATLAB仿真圖

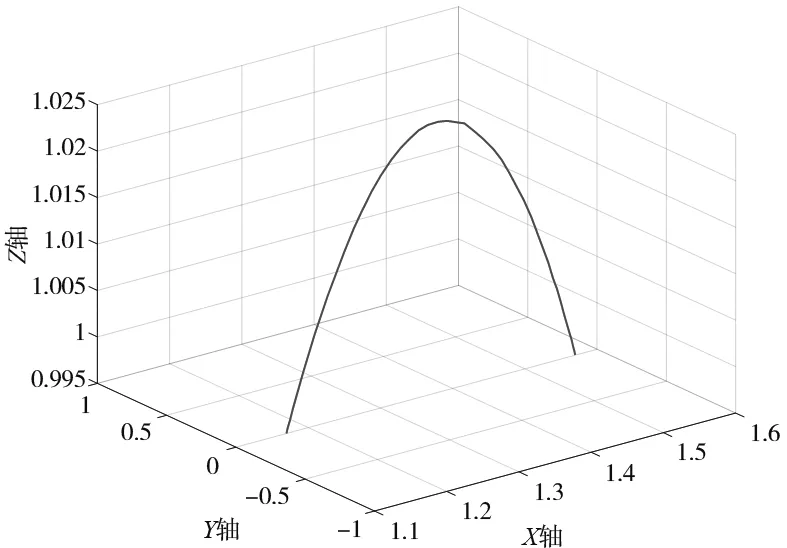
(e) 沿X軸方向KUKA實(shí)際路徑圖

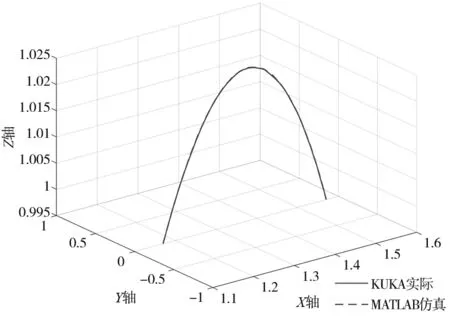
(f) Y軸方向下仿真與實(shí)際路徑對(duì)比圖

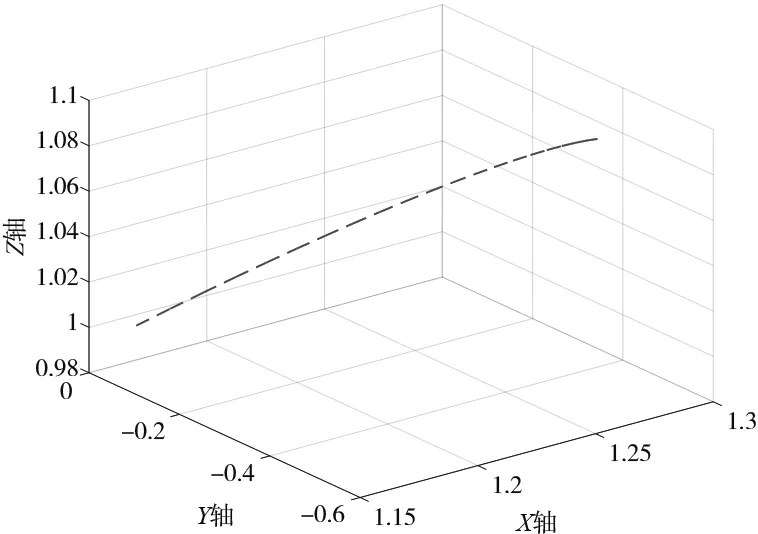
(g) 沿斜線(xiàn)方向MATLAB仿真圖

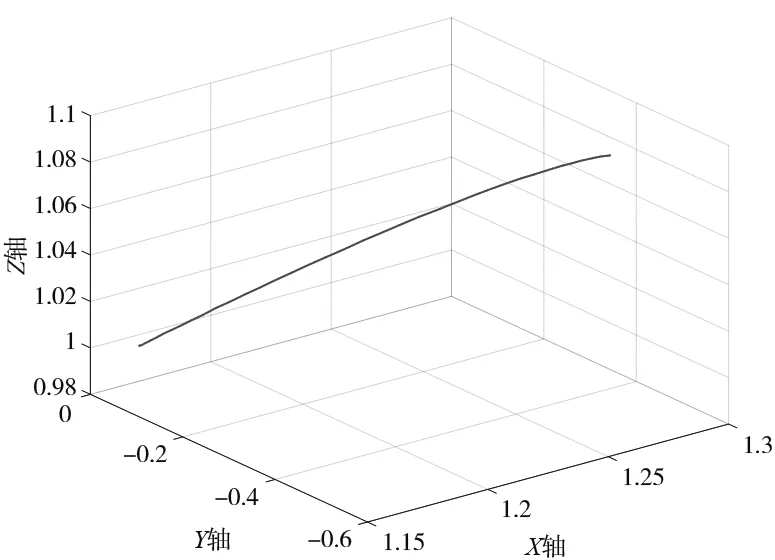
(h) 沿斜線(xiàn)方向KUKA實(shí)際路徑圖

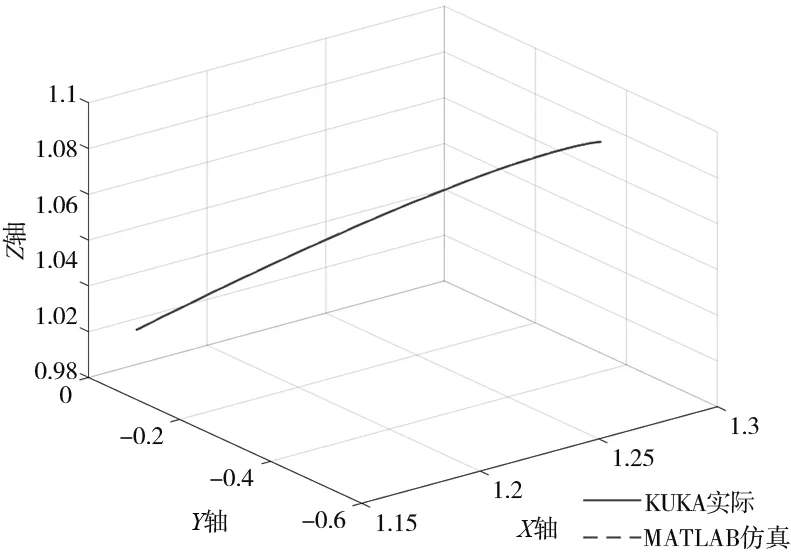
(i) 沿斜線(xiàn)方向仿真與實(shí)際路徑對(duì)比圖 圖4 MATLAB仿真路徑及KUKA仿真路徑

圖4中的9幅圖分別進(jìn)行分析比較：

(1) 圖4a、圖4b是沿Y軸方向坐標(biāo)為(1.17,0,0.995)、(1.17,-0.5,0.995)。圖4a是本算法通過(guò)MATLAB仿真生成的路徑圖；圖4b是MATLAB記錄的KUKA實(shí)際路徑的仿真圖；圖4c是將兩者的路徑放到一起后進(jìn)行的對(duì)比。由圖4b可以看出KUKA機(jī)器人在沿Y軸移動(dòng)的時(shí)候存在一定的抖動(dòng)，路徑并沒(méi)有MATLAB仿真出的理論路徑圓滑，同時(shí)也可以由圖4c看出，兩者基本重合。

(2) 圖4d、圖4e是沿X軸方向，坐標(biāo)為(1.17,0,0.995)、(1.57,0,0.995)。圖4d是本算法通過(guò)MATLAB仿真生成的路徑圖；圖4e是MATLAB記錄的KUKA實(shí)際路徑的仿真圖；圖4f是把兩者的路徑放到一起進(jìn)行對(duì)比。由圖4f可以看出對(duì)比，可以看出兩者幾乎沒(méi)有區(qū)別。

(3) 圖4g、圖4h是沿一條斜線(xiàn)坐標(biāo)為(1.17,0,0.995)、(1.27,-0.5,1.095)。圖4g是本算法通過(guò)MATLAB仿真生成的路徑圖；圖4h是MATLAB記錄的KUKA實(shí)際路徑的仿真圖；同樣圖4i也是將兩者路徑放到一起進(jìn)行對(duì)比，可以看出兩者基本完全重合。

三種情況下姿態(tài)均保持不變，本算法是在笛卡爾坐標(biāo)系下點(diǎn)到點(diǎn)的運(yùn)動(dòng)計(jì)算，KUKA也是在其工具坐標(biāo)下執(zhí)行的PTP(點(diǎn)到點(diǎn))的命令。通過(guò)對(duì)比可以確定兩者路徑相同，在執(zhí)行點(diǎn)到點(diǎn)的命令時(shí)都不是一條直線(xiàn)而是一段弧線(xiàn)。由此可以確定本算法對(duì)于機(jī)器人唯一解的確定具有重要的參考價(jià)值。

3 結(jié)論

普通6自由度工業(yè)機(jī)器人工作空間計(jì)算看似計(jì)算非常復(fù)雜，實(shí)際通過(guò)模型簡(jiǎn)化基于MATLAB進(jìn)行計(jì)算，可以生成和繪圖法相同的工作空間剖截面圖，為機(jī)器人工作空間的計(jì)算以及選型時(shí)需要反復(fù)的確定機(jī)器人工作空間帶來(lái)較大的便利。

通過(guò)對(duì)機(jī)器人運(yùn)動(dòng)學(xué)反解的計(jì)算得出最終的8種解，并對(duì)得出的8種解結(jié)合KUKA機(jī)器人程序的編寫(xiě)以及運(yùn)動(dòng)進(jìn)行分析和篩選，最終確定了機(jī)器人逆運(yùn)動(dòng)學(xué)解的唯一解，并且通過(guò)和KUKA機(jī)器人在相同參數(shù)下運(yùn)動(dòng)情況的對(duì)比，證明了本算法的可行性。