基于氣穴模型的動壓軸承動態油膜剛度計算方法*

(1.上海工程技術大學機械與汽車工程學院 上海 201620；2.上海交通大學機械系統與振動國家重點實驗室，振動噪聲研究所，船艦設備噪聲與振動控制技術國防重點學科實驗室 上海 200240)

液體動壓軸承常用于高轉速及高精度旋轉機械，其可靠性會直接影響到整個機器的精度、使用壽命、經濟性等。動壓軸承一直是轉子動力學和軸承潤滑研究領域的熱點問題，若軸承在設計、安裝、維護等方面有失誤，會出現振動噪聲等,甚至造成重大損失。高轉速下系統的穩定性已成為轉子動力學分析的重要課題，其中的關鍵問題之一是軸承動態剛度的準確計算。

確定油膜的剛度就需要求解油膜力，而求解油膜力就需要求解油膜的壓力分布，理論計算上通常采用不同形式的雷諾方程進行求解，很多學者專家在過去的幾十年間進行了諸多研究。1965年，LUND[1]運用數值計算方法求解雷諾方程，得到了剛度系數，建立了 “軸承-轉子系統”模型，從理論上解釋了系統渦動失穩的形成原因。通常情況下，雷諾方程作為潤滑方程用于計算動壓軸承的剛度[3-5]，但對于雷諾方程求解不可避免地存在一系列的假設，與實際存在一定的偏差。雷諾方程很難準確反映轉子高速轉動過程中引起的周向慣性效應、動態擠壓效應等的影響，油膜剛度計算精度受到影響，因此有必要直接以Navier-Stokes(N-S)方程為基礎，精確研究主軸轉速、位移擾動等對軸心軌跡、油膜剛度等的影響規律。文獻[6]應用基于N-S方程的計算流體動力學軟件FLUENT進行了動壓軸承油膜力的計算研究工作，證實了用流體計算軟件求解動壓軸承油膜力的可行性；文獻[7]進一步引入了動網格模型，計算了基于CFD 動網格模型的液體動靜壓軸承油膜剛度；文獻[8]研究計算了動特性系數，但計算油膜力時沒有考慮氣穴效應；文獻[9]應用FLUENT計算了氣穴影響下的橢圓軸承油膜壓力場，證明考慮氣穴影響對橢圓軸承的模擬結果較不考慮氣穴影響更為合理。本文作者以圓柱徑向動軸承為例，在ADINA軟件中建立流固耦合模型，考慮氣穴效應，直接以Navier-Stokes 方程為基礎，采用ALE法，有效避免了油膜的網格畸變的問題，計算了油膜瞬態壓力場，進而得到軸心軌跡，動態油膜剛度，結合試驗驗證了該計算方法的有效性和可行性，為動態油膜剛度的計算提供了一種方法。

1 剛度計算方法

剛度計算方法是在ADINA軟件基礎上，對軸頸施加正弦位移小擾動，求解N-S方程得到每一個迭代步的軸頸位置變動前后流體的瞬態壓力場和不同方向的瞬態油膜力；結合差分計算模型，計算軸承油膜動態剛度的一種方法。

1.1 剛度的差分計算模型

軸頸在平衡位置受外載荷作用，施加位移小擾動，油膜力會發生變化。在小擾動條件下，軸承油膜剛度可采用差分法求解[7]，如式(1)所示。

(1)

式中:ΔFdij為油膜力的變化；kxx和kyy是直接剛度；kxy和kyx為交叉剛度； Δx和Δy為擾動位移。

采用差分模型計算軸承的剛度需要考慮位移對不同方向油膜力的影響。由式(1)可知，計算油膜剛度系數，需要：①在軸的重力作用下，從初始時刻(軸與軸承同心)狀態下，開始計算瞬態油膜壓力場，該求解是基于氣穴效應的瞬態流固耦合模型，獲得軸心平衡位置，畫出軸心軌跡；②在軸心平衡位置施加軸頸位移擾動，求解瞬態油膜力，得到每一迭代步位移變動前后瞬態油膜力。

1.2 瞬態油膜力控制方程

1.2.1 流體控制方程

在CFD軟件中，油膜流動的基本動力潤滑理論是N-S方程(Navier-Stokes Equations)，不考慮流體的黏溫效應，動力潤滑方程包括連續性方程和動量方程[10-12]:

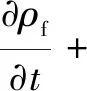
(2)

(3)

式中：t是時間；ρf是流體密度；τf是流體區域的應力張量；v是速度矢量；ff是流體部分的體力矢量。

τf=(-p+λ·v)I+2μe

(4)

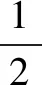
用任意的拉格朗日-歐拉(ALE)公式求解上述方程，從而求得流體區域的變形。

1.2.2 固體域控制方程

對固體域施加位移擾動時，固體域的控制方程可用式(5)描述。

(5)

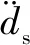
1.2.3 流固耦合方程

在流固耦合界面上，流體和固體將同時滿足位移和力平衡的條件。位移協調方程和力平衡方程分別如式(6)和(7)所示。

df=ds

(6)

n·τf=n·τs

(7)

式中：df和ds是流體和固體在流體-結構界面上的節點的位移;τf和τs是流體和固體在流體-結構界面上的節點的應力；n是方向向量。

以上參數僅在流固耦合面上。流固耦合方程采用直接法求解，耦合面上滿足力和位移平衡條件，當力和位移的相對殘差小于0.01時即認為該迭代步收斂。

1.2.4 氣穴模型

不采用氣穴模型時，軟件模擬時油膜壓力分布中存在較大負壓，會導致油膜力計算偏差較大[9]。文中流體計算采用了相變模型。流體和氣體相變通過求流體域壓力函數的導數來實現。SUN和BREWE[13]曾說明這種相變模型能夠真實反映薄油膜動態情況下氣相的變化情況。計算中，潤滑油看成不可壓縮的流體，氣相看成可以輕微壓縮的流體。氣相的體積分數f通過氣體的體積與總體積的比來確定。m定義為任意情況下流體-氣體的體積比，由下式得到：

m=ml+f(mv-ml)

(8)

式中：下標l表示流體，v表示氣體。

當流體壓力p大于定義的蒸發壓力plv時，氣相分數f=0；當流體壓力p小于定義的冷凝壓力pvl時，氣相分數f=1。用如下函數近似定義氣相體積分數的變化(式中α=0.1)：

(9)

(10)

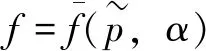
(11)

冷凝壓力(pvl)的取值通過敏感性分析后確定。假設軸為剛體，計算冷凝壓力為-20、-60、-80 kPa時軸心位置；在取該壓力值時，軸心位置的偏差小于1%。文中計算，蒸發壓力(plv)和冷凝壓力(pvl)分別取0和-60 kPa。

2 典型軸承的油膜剛度計算

2.1 軸承結構和建模

按試驗臺中徑向圓柱動壓軸承(如圖1所示)尺寸建模，主軸軸頸直徑是40 mm，軸承的直徑是40.08 mm，軸承軸瓦的長度是32 mm。該軸承承受主軸重量為150 N，在ADINA中完成軸和油膜的流固耦合模型[14]，采用六面體網格劃分模型，油膜周向劃分320份,軸向劃分30份，厚度方向分5層，共48 000個單元；軸的周向劃分320份,軸向劃分10份，徑向劃分12份。軸和油膜網格模型如圖2所示。假設流體不可壓縮，等溫、黏度不變，層流。采用式(8)—(11)所表示的氣穴模型，油膜與軸接觸面施加切向速度，油膜與軸瓦接觸的表面定義為固定壁面，軸上施加重力150 N，軸與流體的接觸面定義為流固耦合面，采用瞬態分析。

圖1 徑向軸承結構

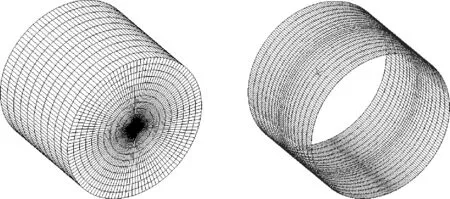
圖2 三維模型網格圖

2.2 軸心軌跡

求解時，初始位置軸與軸襯同心，油膜各個方向厚度相同，然后在軸的重力作用和軸頸轉速共同作用下移動，油膜厚度發生改變，油膜產生油膜力，軸心位置不斷改變。在Δλ/ΔY≤2%時(如圖3所示)，認為軸到達平衡位置。圖3中，ΔY為任意周期內點A、B坐標的平均值的絕對值(水平橫線)。Δλ為點A或點B坐標到該橫線距離中的較小值。轉速為2 500 r/min時軸心軌跡如圖4所示，1.2 s時達到平衡位置。

圖3 軸心位置判斷方法

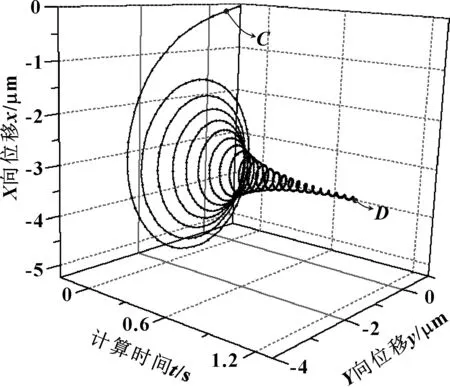
圖4 軸心軌跡

2.3 瞬態壓力場

油膜的壓力分布隨軸心軌跡的變化而變化，初始時刻，油膜厚度各個方向相同，無油膜壓力，在0.001 s時(圖4中點C)油膜壓力場如圖5(a)所示, 油膜壓力分布最大值為0.3 MPa，隨著油膜壓力場的變化，軸心上浮慢慢穩定下來，油膜壓力分布最大值略有降低，迭代至1.2 s時(圖4中點D)，油膜壓力分布最大值為0.27 MPa，如圖5(b)所示。

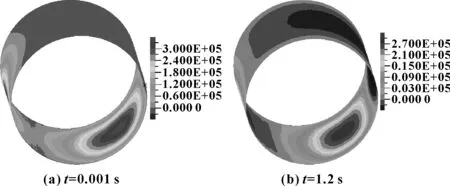
圖5 不同時刻油膜壓力分布

2.4 動態剛度

通過計算軸心軌跡，確定軸心平衡位置，然后再對軸施加正弦擾動，得到各個迭代步的瞬態油膜力，通過式(1)，來確定動態油膜剛度。以軸頸轉速為2 500 r/min為例，計算油膜4個動態剛度kxx、kxy、kyx、kyy，其數值的數量級多為6、7、8，如圖6—9所示。計算時每間隔4.88×10-4s讀取對應位移與力的數值，總共讀取2 048對數據，以對應試驗時的2 048個采樣點，各剛度值的數量級個數統計如圖10所示。

圖6 動態油膜剛度kxx

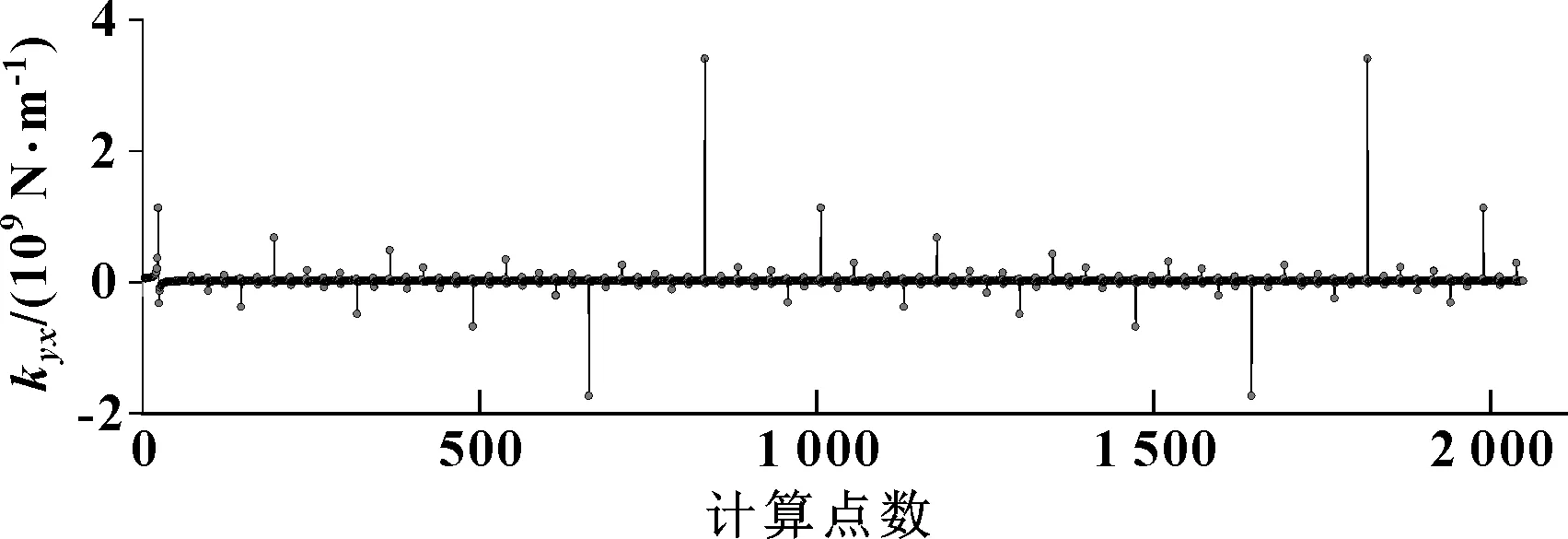
圖7 動態油膜剛度kyx

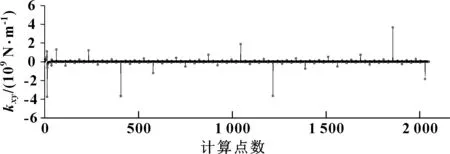
圖8 動態油膜剛度kxy

圖9 動態油膜剛度kyy

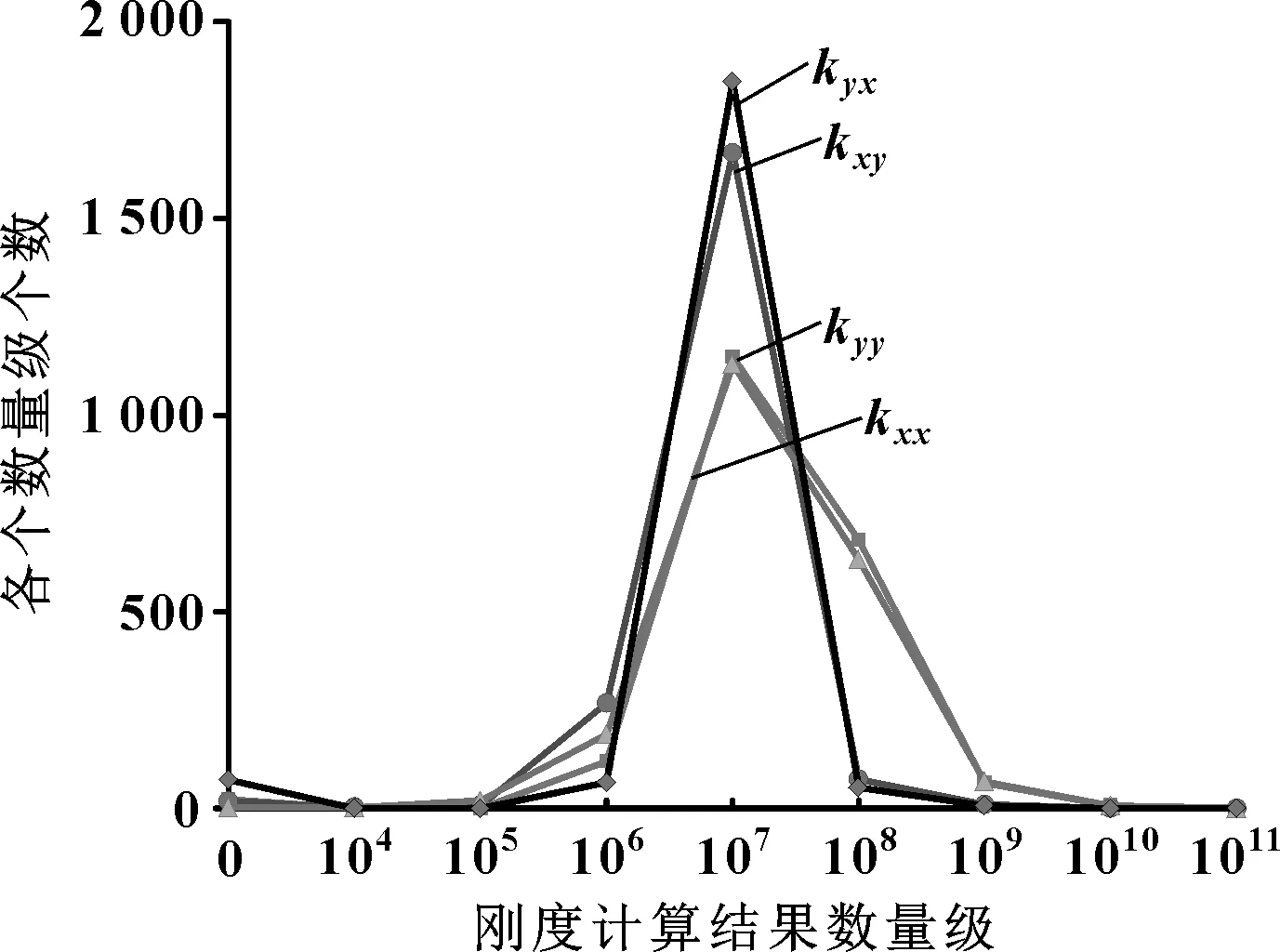
圖10 剛度的數量級個數

3 試驗研究

試驗臺示意圖、結構圖如圖11、12所示，試驗和數值計算主要是研究軸承2的油膜剛度，傳感器安裝于軸承上，傳感器輸出的信號相對于軸瓦是離散數值，對離散點進行擬合得到軸瓦上動態油膜壓力分布情況[15]。

圖11 試驗臺示意圖

圖12 試驗系統布置圖

試驗測得下半瓦傳感器的一階頻譜幅值比上半瓦的一階頻譜幅值要大7倍，也就是下半瓦上測得的壓力值要比上半瓦的大，這與數值模擬的結果相符。測量剛度時，采用電渦流位移傳感器在主軸運轉中記錄下振動位移情況，第一時刻，記錄下油膜力和振動位移；第二時刻，記錄下油膜力和振動位移，這些參數就可以計算動態油膜剛度。轉速為2 500 r/min，信號是在時間1 s內進行了個2 048個點的采樣，計算得到動態剛度系數如圖13所示。kxx、kxy、kyx、kyy數值的數量級多為6、7、8，總體與數值計算結果相符。由于數值計算時假設潤滑油不可壓縮、油溫不變，忽略了主軸不平衡等因素，而試驗時可能存在轉子質量動不平衡、軸承加工誤差等問題，會影響油膜動剛度系數的準確性，因此仿真結果和試驗之間局部各數據點并非完全一致，但仿真結果與以上實測動態剛度數值相比較發現油膜動態剛度的變化趨勢是一致的，兩者基本吻合，說明基于氣穴模型的數值仿真計算方法是可行和有效的，為動態油膜剛度的計算提供了一種方法。

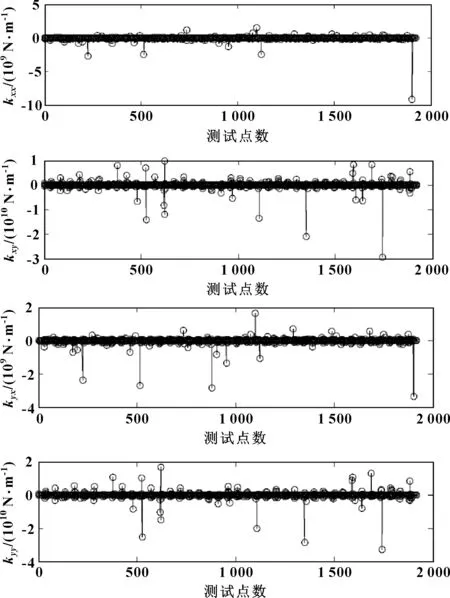
圖13 動態油膜剛度系數

4 結論

(1)采用瞬態分析，基于流固耦合方法和氣穴模型，軸在重力和油膜力的作用下從軸與軸襯同心開始計算，逐漸穩定在平衡位置，再現了軸心動態平衡過程，計算過程更加符合工程實際。

(2)數值仿真油膜動態剛度與實測動態剛度數值的變化趨勢是一致的，兩者基本吻合，說明基于ADINA軟件的數值仿真計算方法是可行和有效的，為動態油膜剛度的計算提供了一種方法。

(3)計算得到的油膜力和油膜厚度的動態發展過程、軸心軌跡和動態剛度在軸承設計中考慮瞬態階段的安全性方面提供了理論上的依據。