除霜器噪聲特性的仿真研究

邵士前，樊劉楊，豆騰堯，閆偉

(山東大學能源與動力工程學院,山東濟南 250061)

0 引言

商用客車作為一種遠程交通工具，對乘客的乘坐舒適性要求較高，客車噪聲是影響乘客舒適性的重要因素，需要對客車的噪聲進行有效控制。客車噪聲主要有車內噪聲和車外噪聲，車內噪聲又分為固體聲和空氣聲，其中固體聲是車內固體振動產生的噪聲，空氣聲是車內空氣波動產生的噪聲；車外噪聲主要由車身、輪胎與外界空氣接觸產生。近年來，隨著發動機技術的突飛猛進，發動機噪聲降低的幅度較大。對發動機之外的部件進行噪聲控制是降低汽車噪聲另一條重要途徑[1]。除霜器作為客車必不可少的部件，是車內噪聲的主要來源之一，對其噪聲進行有效的控制可以提高乘客的舒適性。在噪聲仿真方面，楊博[2]應用穩態雷諾平均那維爾-斯托克斯方法較準確地定位了汽車外部噪聲的主要來源。張群峰等[3]對比了分離渦仿真和非線性聲學方法仿真腔體啟動噪聲的效果，找出兩者產生差別的原因。徐志超[4]運用混合計算方法，推測發動機進氣啟動噪聲產生的原因。劉厚林等[5]應用大渦仿真方法找出引起離心泵隔舌處壓力脈動的主要原因。鄧曉龍等[6]應用大渦仿真方法模擬推導汽車暖風通道的噪聲特性。

1 研究對象

某款除霜器結構如圖1所示，其主要部件為散熱器和風扇。散熱器下部是網狀進風口，上部有3個出風口，2個大出風口直徑7.5 cm，一個小出風口直徑3 cm。除霜器設計高、中、低3擋。風扇最大轉速為2000 r/min，理論通風量為1200 m3/h。除霜器風扇采用鼠籠式風扇，共有2個風扇，每個風扇有28片扇葉。散熱器采用翅片式散熱器。

聲音是由空氣的脈動產生。空氣在脈動過程中，壓力由P0變化為P0+ΔP，ΔP為聲壓[7]。流體噪聲是流體經過物體表面時產生的噪聲。流體噪聲的噪聲源分為單極子聲源、偶極子聲源和四極子聲源[8]3種。單極子噪聲由1個點振源產生，偶極子噪聲是物體表面共振作用產生的噪聲。四極子噪聲主要由風扇產生，是風扇在旋轉時引起空氣渦流破碎而產生的噪聲[9]。該除霜器產生的噪聲主要是四極子噪聲。

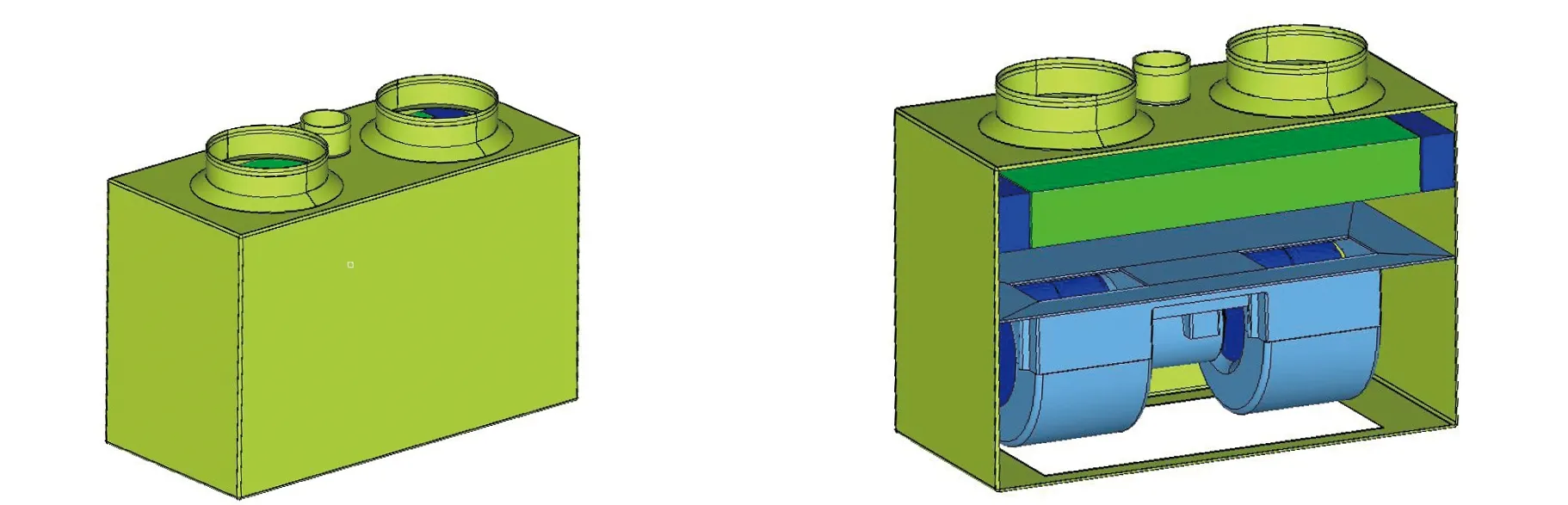
a)整體外形 b)內部結構圖1 除霜器結構圖

Lighthill首次提出流體噪聲產生機理，由流體學基本運動方程和連續性方程推導出流體噪聲產生的Lighthill機理公式為[10]

(1)

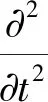
2 建模

2.1 網格模型

對該款除霜器模型做幾何處理，簡化表面結構。在hypermesh中生成面網格。面網格模型選用三角形網格，共計131萬個面網格。將生成的面網格導入STAR CCM+中生成體網格，網格模型選用多面體網格生成器和棱柱層網格生成器，共生成684萬個體網格。對風扇區域進行加密處理，以便更好地捕捉細節。棱柱層厚度為2 mm，層數為5層，棱柱層延伸為1.5，并生成計算域。除霜器網格劃分模型如圖2所示。

a)整體外形 b)內部結構圖2 除霜器網格劃分模型

2.2 物理模型

對除霜器周圍的流體區域選擇理想氣體作為物理模型，采用非定常仿真，采用氣動聲學模型中的Ffowcs Williams-Hawkings 非穩態模型和飛行中的 FW-H 模型[11]。渦流模型采用分離渦[12]仿真進行結果對比。分離渦仿真結合RANS方法在近壁面湍流處理的優勢和LES處理遠離壁面的大渦湍流的優勢[13]。對固體區域建立三維恒密度分離固體能量的隱式不定常模型[14]。對散熱器區域采用多孔介質模型，其黏性阻力系數為80 kg/(m3·s)，慣性阻力系數為25.0 kg/m4，孔隙率為0.9，湍流黏度比為10。

Ffowcs等[15]于1969年在廣義函數理論的基礎上推導出FW-H方程，該方程表示流體在由靜止到任意運動的過程中噪聲的產生方式。FW-H 模型是在流體力學N-S方程的基礎上按照非齊次波動方程的規律重新規劃整理得到的，能夠準確計算流體在由靜止到任意運動時產生的噪聲，是氣動噪聲學的基礎理論之一。本文中采用飛行中的FW-H模型。假設控制面方程為

f(xi,t)=0,▽f=ni，

式中:ni為控制面上單元的外法線上的矢量方向,Vn表示的是控制面上單元的速度。

FW-H模型最常用的公式為:

(2)

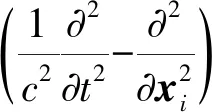
2.3 邊界條件

圖3 除霜器計算域

在除霜器周圍建立1個方形的計算域仿真真實空間，如圖3所示。在計算域中建立新的笛卡爾坐標系。計算域進口設置為壓力進口，出口設置為壓力出口。對于風扇采用MRF模型。在風扇周圍設置旋轉區域。旋轉區域與空氣之間以界面形式連接，對風扇采用靜網格而不是動網格，可以大大減少計算量，節約計算時間。各邊界采用多面體網格形式，為了更好地捕捉細節，邊界層層數設為5。各部分的具體屬性如表1所示。

表1 邊界條件

3 仿真結果分析

3.1 穩態仿真

對除霜器流場先進行穩態仿真分析，通過在進出口建立質量流量報告獲得進出口面上的質量流量。當進出口質量流量誤差小于0.5%時，認為仿真已經收斂。在穩態分析中，風扇轉速分別選用了1500、1750、2000 r/min，得到3種轉速下進出口質量流量及誤差如表2所示。

表2 不同轉速下的進出口質量流量

從表2可以看出，3種轉速下進出口質量流量誤差均在0.5%以內，可以認為穩態仿真已經收斂。取2000 r/min轉速條件下的仿真結果分析除霜器流場，截面x=-20 mm上的速度場如圖4所示(圖中單位為m/s)。

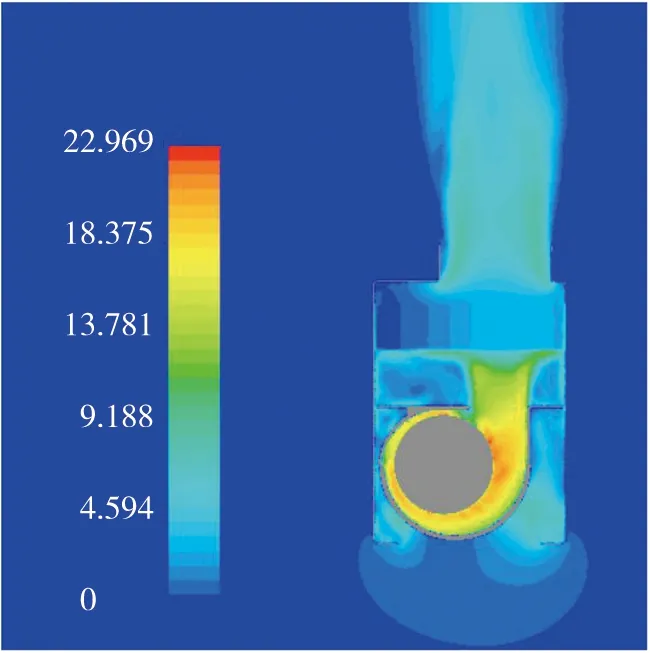
圖4 x=-20 mm截面速度場

從圖4可以看出，除霜器在工作過程中，風扇表面氣流速度較大，最大達到15.6 m/s。出口處由于截面積突然減小，空氣流速急劇增加。散熱器處由于具有多孔結構，造成節流效果，空氣流速有所降低。

圖5所示為穩態仿真中得到的風扇表面空氣壓力場(圖中單位為Pa)，圖6為除霜器外殼的空氣壓力云圖(圖中單位為Pa)。從圖5可以看出，風扇表面空氣壓力在中心處比較小，在風扇翅片表面處壓力比較大，風扇在迎風面上的壓力遠大于背風面，這是噪聲產生的主要原因之一。從圖6可以看出，在風機出風口處，空氣直接吹到外殼壁面上，外殼出風口處由于截面積減小，導致上壁面空氣壓力比較大，也是噪聲產生的原因之一。

圖5 風扇表面壓力分布云圖 圖6 除霜器外殼壓力云圖

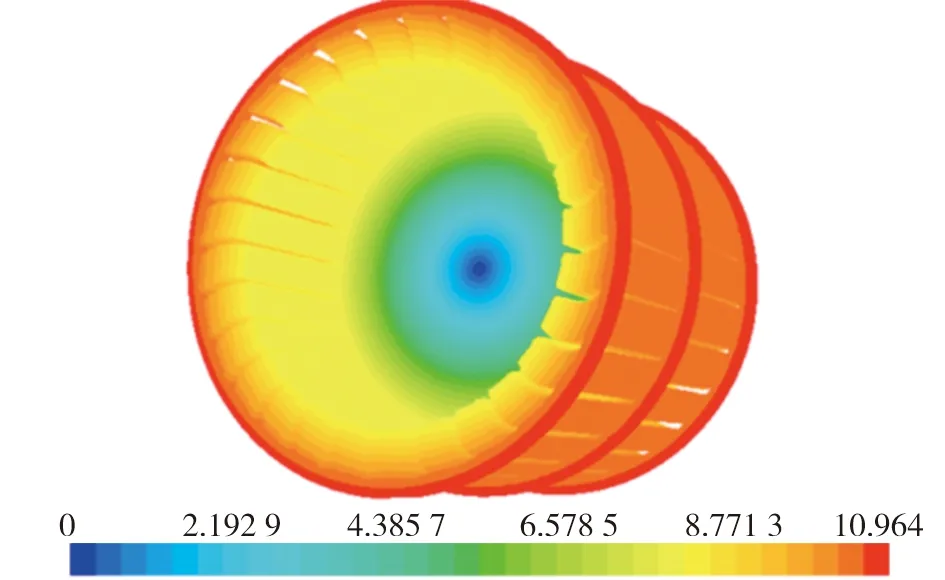
圖7 風扇表面速度矢量云圖

圖7所示為風扇轉速為2000 r/min時風扇表面的空氣速度矢量圖(圖中單位為m/s)。從圖7可以看出，風扇表面的空氣速度從中間向外依次增加，最大速度出現在最外層葉片表面，為10.964 m/s。風扇半徑為52.5 mm，經計算可得理論風扇邊緣最大速度應為10.99 m/s。仿真結果與理論值誤差小于0.1%。

3.2 瞬態仿真

在穩態仿真的基礎上，將模型時間改為不定常類型，湍流模型分別應用分離渦模型和大渦模型，風扇轉速選用最高轉速2000 r/min。在Ffowcs Williams-Hawkings 非穩態模型，應用飛行中的 FW-H 模型，時間步長設為8.33×10-5s，每5步迭代1次，總時長設為1.2 s。使用飛行中的 FW-H 模型時將不滲透面設為風機，風扇表面以及除霜器外殼作為噪聲源，在除霜器出口1 m處設置一個接收點，用來接收聲壓。穩定后進口質量流量為0.499 5 kg/s，出口質量流量為0.498 7 kg/s，誤差為0.16%，小于0.5%，說明計算結果收斂。

圖8是通過監測點得到的出口1 m處的壓力變化曲線，對噪聲聲壓信號在時域內采用等效連續聲壓級進行分析。傅里葉變換可以將1個時域信號轉換成在不同頻率下對應的振幅及相位，其頻譜就是時域信號在頻域下的表現。

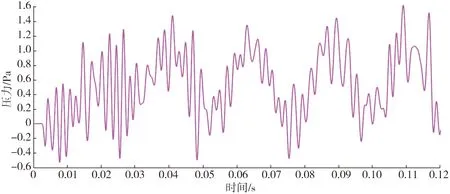
圖8 出口1 m處的壓力變化曲線

對圖8中的聲壓信號進行快速傅里葉變換得到頻域內客觀聲壓級曲線，如圖9所示。快速傅里葉變換是離散傅里葉變換的一種快速算法。離散傅里葉變換的基本公式如式3[16]所示，數據序列x(n)長度設為M，則定義x(n)的N個點DFT(離散傅里葉變換)為:

(3)

式中N為離散傅里葉變換區間長度，要求N≥M。

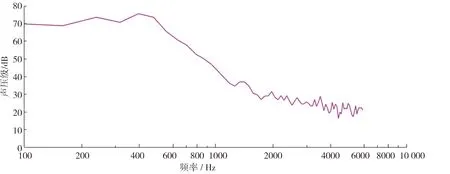
圖9 出口1 m處聲壓級曲線

人對聲音的感知與聲壓變化有關，同時與聲音的頻率也有關系。A計權聲壓是根據人體對聲音的感知，通過對每個頻率上的聲壓進行加權，得到一個更加符合人體感知的聲壓曲線。在頻域內對A計權聲壓級[17]

(4)

式中：A1000為1000 Hz對應的聲壓級；f為計算頻率，Hz；f1=20.6 Hz;f2=107.7 Hz;f3=737.9 Hz;f4=12 194 Hz。經計算可得總的A計權聲壓級為73.34 dB。

將圖8經過快速傅里葉變化可得A計權聲壓頻譜圖，如圖10所示。從圖10可以看出，A計權聲壓在線性計權聲壓的基礎上低頻噪聲的部分衰減極大，忽略了低頻噪聲的危害。為了更好地看出噪聲分布的頻率范圍，繪制1/3倍頻的A計權聲壓級，如圖11所示。

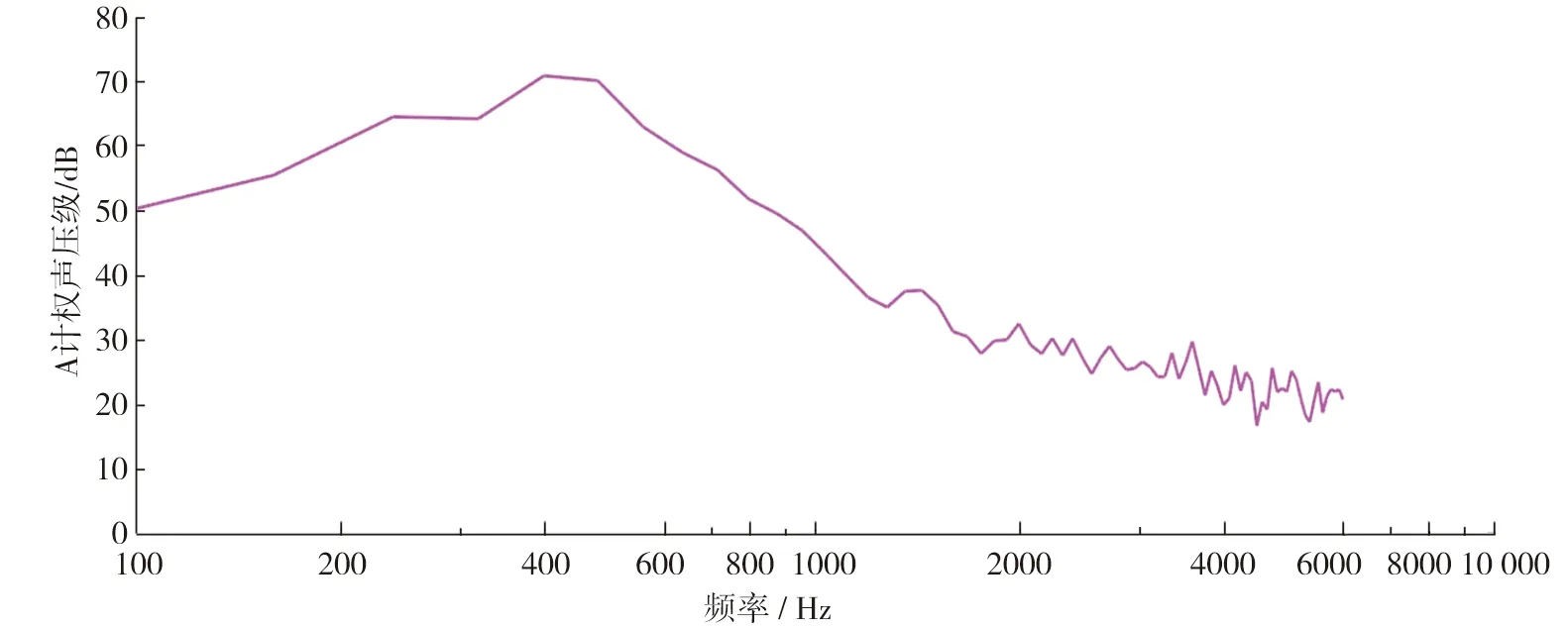
圖10 A計權聲壓級

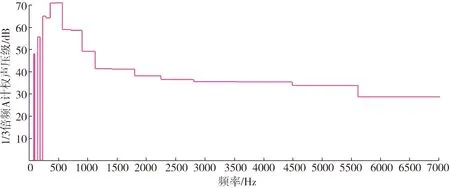
圖11 1/3倍頻A計權聲壓級

從圖11中可以看出，低頻噪聲的聲壓級較大，高頻噪聲的聲壓級較低。較高的聲壓級集中在200～900 Hz，最高聲壓級接近70 dB，出現在500 Hz附近。

3.3 試驗驗證

試驗采用丹麥公司B&K生產的PULSE(聲學)材料測試系統，應用配套PULSE 21.0對測試得到的聲壓進行分析。圖12是試驗中得到的聲壓頻譜隨時間變化得到的map圖，測試時間為60 s，測試點在除霜器出口1 m處。

圖12 60 s聲壓頻譜隨時間變化map圖

圖13是試驗得到的A計權聲壓級圖，圖14為仿真得到的A計權聲壓級圖。由圖13可以看出試驗總的A計權聲壓級73.4 dB，由圖14可以得到總聲壓級為73.34 dB，誤差為0.08%，仿真結果符合真實情況。

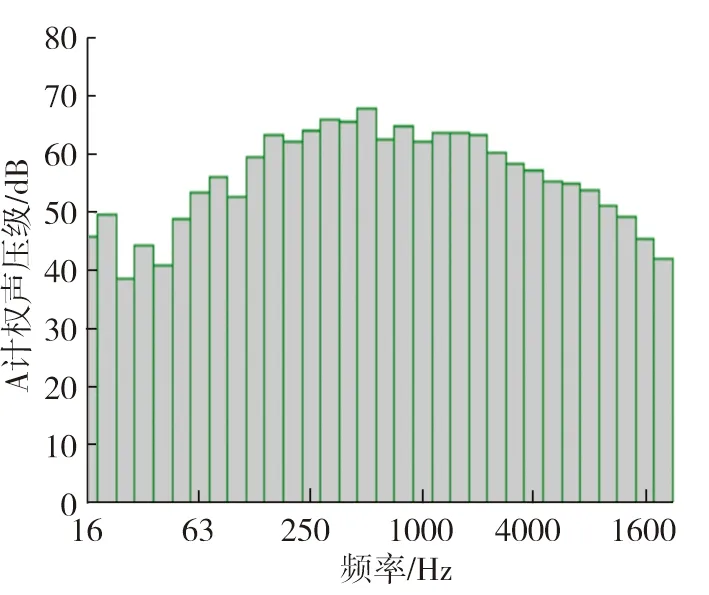
圖13 試驗A計權聲壓級圖

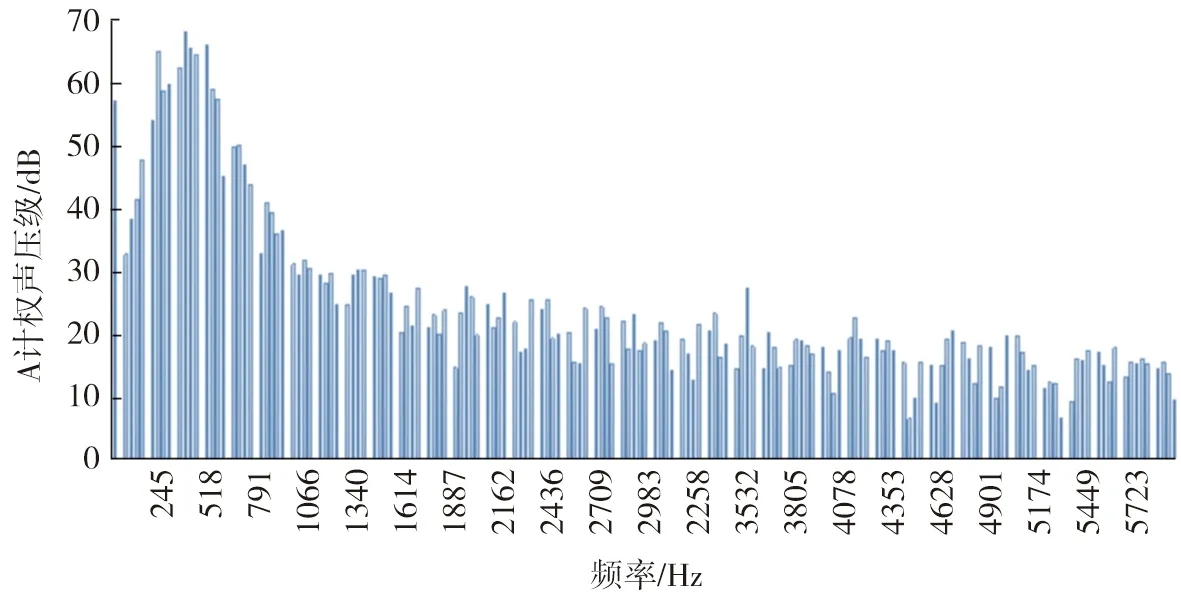
圖14 仿真A計權聲壓級圖

圖13～14經處理得到1/3倍頻A計權聲壓圖，如圖15、16所示。

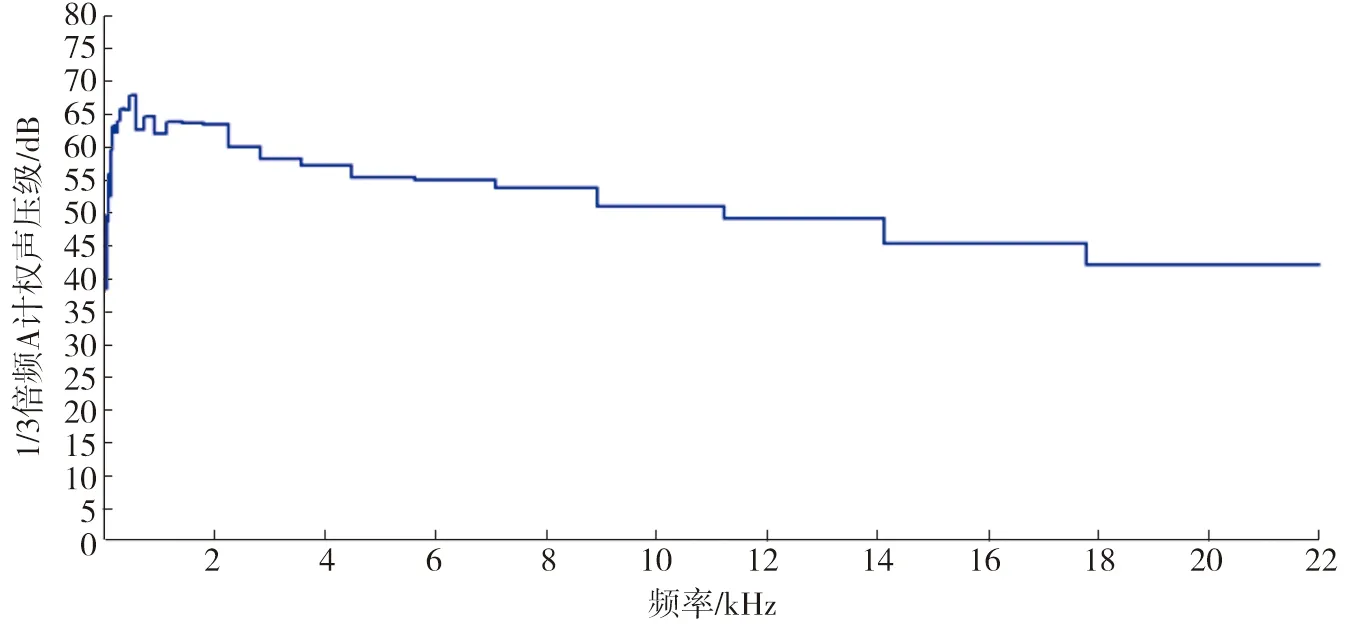
圖15 試驗1/3倍頻A計權聲壓級圖

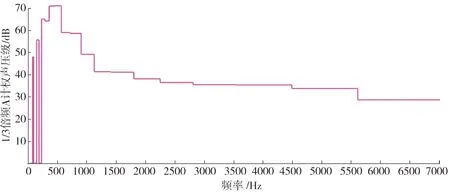
圖16 仿真1/3倍頻A計權聲壓級圖

從圖16可以看出，在頻率150～1000 Hz出現高聲壓級，這與仿真得到的高聲壓級分布范圍大致相同。最大聲壓級接近68 dB，仿真結果最大聲壓級為70 dB，誤差為2.9%。從圖16中可看出高分貝所在頻率為150～1000 Hz。綜上所述，仿真結果與試驗結果誤差在5%以內，仿真方法得到驗證。

4 結論

對某款除霜器的噪聲進行仿真計算，分析該噪聲產生的原因及噪聲源位置。利用網格劃分軟件對除霜器進行劃分，再利用STAR CCM+軟件對除霜器進行物理建模，通過計算得到該款除霜器在轉速2000 r/min時的聲壓，并通過快速傅里葉變換得到其A計權聲壓級圖，通過試驗得到該款除霜器在轉速2000 r/min時的噪聲數據。

通過對比試驗數據與仿真數據中的A計權聲壓級圖以及1/3倍頻聲壓級圖，可以看出，仿真結果中高分貝頻率為150～1000 Hz，為中低頻率，試驗結果與其趨勢大致相同，誤差小于5%。試驗得到的總的聲壓級為73.4 dB，仿真得到的聲壓級為73.34 dB，誤差為0.08%，驗證了該仿真方法的可行性。

通過以上分析可知，該款除霜器噪聲是風扇噪聲與除霜器外殼振動噪聲共同組成，下一步可以通過增大除霜器外殼厚度降低振動以及優化風扇翅片等措施來降低除霜器噪聲。