黃河近百年徑流演變特征分析

胡慧杰，崔 凱，曹 茜，李姝蕾，常肖杰，沈麗娜

（1.河南黃河水文勘測設計院，河南鄭州450004；2.黃河勘測規劃設計研究院有限公司，河南鄭州450003；3.河南省許昌水文水資源勘測局，河南許昌461000）

受氣候變化的影響和人類活動的干預,流域水循環規律逐漸發生變化,徑流演變規律也隨之改變。河川徑流量是流域水資源科學開發利用、合理調度配置的基礎［1］,因此研究徑流演變特性對流域水資源的高效利用、合理規劃具有重要意義。

黃河是我國的第二大河,承擔著流域供水、灌溉、防洪、防凌、生態等多方面任務。黃河水情的不利形勢將對沿黃地區的工農業生產、生態環境造成極大影響,研究黃河徑流的演變過程,分析其演化特性,有助于深刻認識水資源變化規律,科學控制水資源開發利用過程。近幾年很多學者對上游唐乃亥站徑流有較深入研究［2］,而對黃河下游花園口水文站徑流研究不多。花園口水文站是國家級水文站,地處黃河中下游的節點部位［3］,發揮著為黃河下游防洪調度與水資源管理提供重要水文信息的作用。花園口水文站以上的匯流面積占黃河流域總面積的97%,來水量占黃河總水量的96.6%,因此花園口水文站來水量大小基本反映黃河水量的豐、枯狀況,分析花園口水文站近百年（1919—2016年)的徑流演變可以反映黃河流域的徑流演變特性,從而為黃河水資源配置調度及管理規劃提供重要的參考依據。

1 數據來源

花園口水文站1938年建站,1949年1月起有連續的觀測資料,建站之前的徑流數據根據陜縣站1919年以來的徑流量插補延長［4］,最終得到花園口水文站1919—2016年各水文年（7月至次年6月)的天然徑流量。本文采用經過還原的天然徑流時間序列分析黃河徑流的演變規律。

2 數據分析

徑流時間序列是水文時間序列的一種,一般包含確定成分和隨機成分。為深刻反映黃河流域徑流變化規律,本文運用水文時間序列分析方法,對徑流數據的突變點及突變前后的趨勢性進行分析。

2.1 統計特征分析

水文學常用的統計特征值包括平均值、極值、極差、均方差、變差系數、偏態系數、年際極值比等［5］。其中,變差系數和極值比反映的是徑流的相對變化程度,這兩個特征值越大表明徑流的年際變化越劇烈,徑流資源的利用難度越大,對水資源管理的要求越高［6］,反之,則表示徑流的年際變化較為平緩,有利于水資源的開發利用。

花園口1919—2016年各水文年度的徑流量變化見圖1,其中：1964—1965年度的天然徑流量最大,為938.7億m3；2002—2003年度的天然徑流量最小,為257.4億m3。徑流量最大值為最小值的3倍多,極差為681.3億m3,說明黃河來水年際間相差較大。

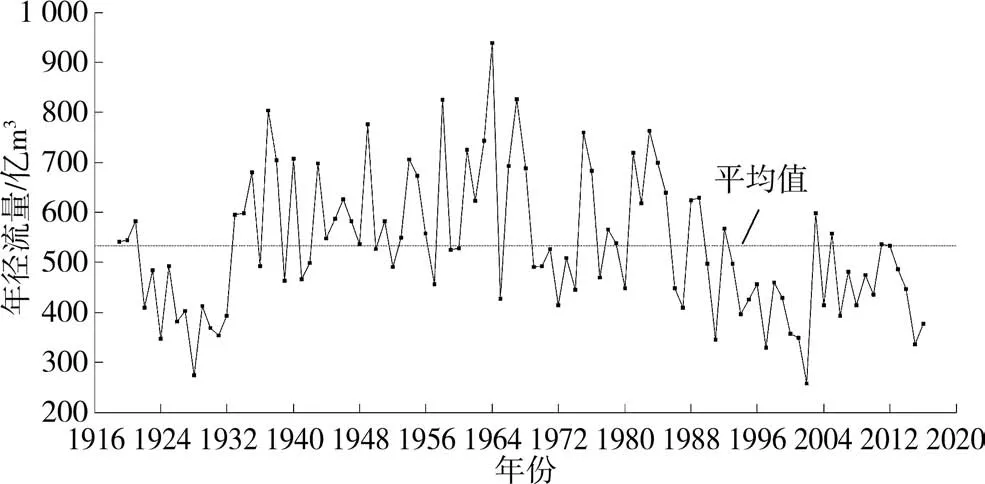
圖1 花園口水文站年天然徑流量變化過程

1919—2016年多年平均徑流量為532.5億m3,標準差為135.4億m3,變差系數為0.25。第一個黃河流域規劃于1955年通過,此后開展了黃土高原水土流失治理,建設了一大批淤地壩；流域第一座大型年調節水庫龍羊峽水庫1986年建成并投入使用；1999年開始實施全河統一水量調度。按以上重要年份將徑流時間序列分為不同的時段,各時段的特征值見表1。其中,1956—2016年的標準差較大,其序列值較為分散,即1956年以來徑流量年際變化較為劇烈,徑流資源的利用難度較大。

1956—1986年徑流量平均值為606.1億m3,變差系數為0.23,相對1956—2016年的變化較為集中。1987—2016年徑流量均值為450.6億m3,變差系數為0.20,偏態系數、極差相對1956—1986年均較小。可見,1987年以來黃河徑流相對集中,極差為373.0億m3,而1999年以來黃河來水較少并出現負偏現象。

表1 各時段徑流時間序列特征值

從特征值分布來看,1956—1986年徑流量平均值最大,1999—2016年徑流量平均值最小,表明1956—1986年黃河來水相對較多。1999—2016年徑流量標準差及變差系數最小,其次是1987—2016年,即近30 a的黃河來水變化相對較為平緩。1956—2016年徑流量偏態系數最大,正偏幅度最大；各時段中只有1999—2016年偏態系數為負,出現負偏。1919—2016年與1956—2016年兩時段的極差最大,極差最小的時段為 1999—2016年,其次為1987—2016年,可見近30 a黃河流域的來水變化幅度相對較小。

2.2 突變分析

突變分析即對數據序列的變異進行診斷,突變主要包括均值突變、方差突變、趨勢突變、概率突變、譜突變、模型參數突變等幾種類型［7］。水文時間序列的突變主要指均值突變或趨勢突變,即時間序列從一個均值狀態或者趨勢突然跳躍到另一個均值狀態或趨勢的突變［8］。突變分析常用的方法主要包括有序聚類分析法、Mann-Kendall突變檢驗法、滑動t檢驗法等。

2.2.1 有序聚類分析法

有序聚類分析法是通過統計分析提取序列突變點的有效方法,主要思想是利用離差平方和判斷突變點,認為同類之間的離差平方和最小,而類與類之間的離差平方和最大［9］。采用該方法可以分析水文時間序列中徑流量或降水量的突變點。

設有水文時間序列xt（x1,x2,…,xk-1),突變點為τ,則突變前后的離差平方和分別為

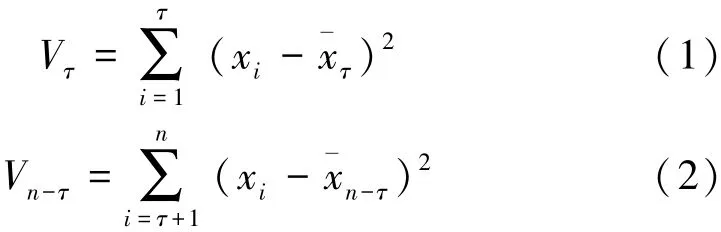
式中：ˉxτ、ˉxn-τ分別為τ前后兩部分的均值。

總離差平方和為

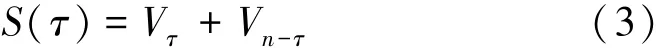
取S（τ) 的極小值,則當S＝minSn（τ) （2≤τ≤n-1)時,分割點兩側的離差平方和最小,即τ為最優二分割（突變點)。

運用有序聚類分析法對花園口水文站的年徑流量時間序列進行突變點分析,計算與τ對應的Sn（τ),點繪Sn（τ)變化曲線（見圖 2)。 由圖 2可知,Sn（τ)最小值出現在1990—1991年度,該年度為最可能的突變點。1933—1934年度Sn（τ)局部最小,故該年度也可能是突變點。因此,花園口水文站年徑流量可能在1990—1991年、1933—1934年發生了突變。

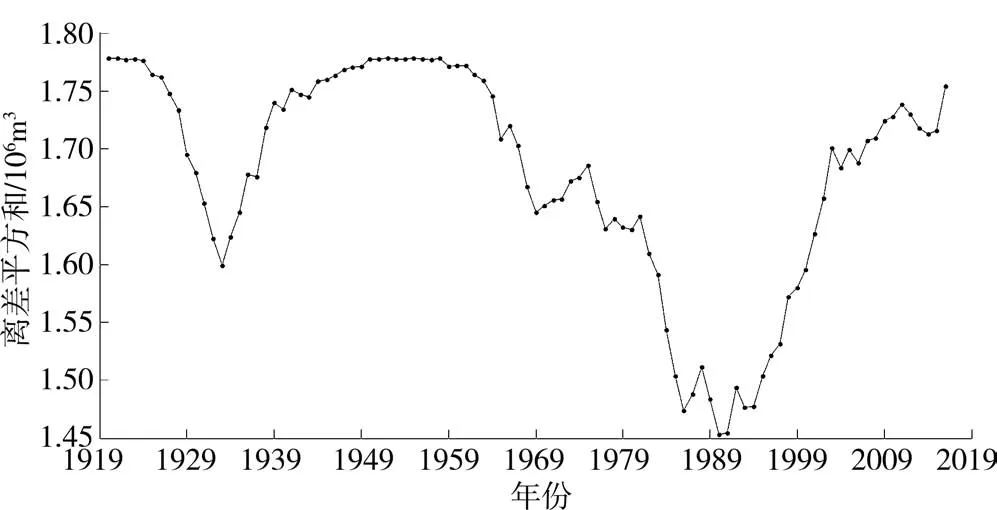
圖2 花園口水文站年徑流有序聚類S變化曲線

2.2.2 Mann-Kendall突變檢驗法

Mann-Kendall突變檢驗法廣泛應用于非參數檢驗,是時間序列分析常用方法之一［10］。該方法由Mann和Kendall于1954年提出,近年來被廣泛應用于分析徑流、氣溫、降水和水質等要素時間序列的突變情況。Mann-Kendall突變檢驗法不要求被分析樣本遵從一定分布,也不受其他異常值的干擾,適用于氣象、水文等非正態分布數據,計算十分簡便。應用Mann-Kendall突變檢驗法進行序列突變檢驗時,對時間序列xt（t＝1,2,…,n),構造一秩序列［11］：

其中

定義統計量：

其中

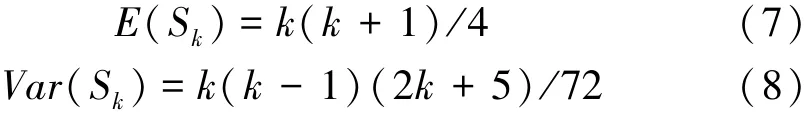
式中：E（Sk)和Var（Sk)分別為累計數Sk的均值和方差。

將時間序列xt（t＝1,2,…,n)按降序排列,再按式（8)計算,同時使

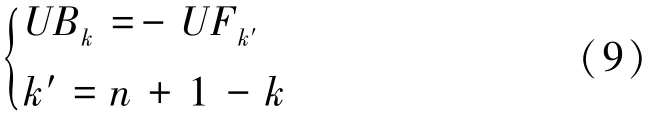
當k＝1時,UF1為0,服從標準正態分布。

運用Mann-Kendall突變檢驗法檢驗時間序列的突變性時,將UFk和UBk兩條統計量序列曲線和顯著性水平為0.05的正態分布值U0.05＝±1.96兩條臨界線繪制在同一張圖上。如果UFk和UBk兩條曲線在兩條臨界線U0.05＝±1.96之間相交,則說明該序列有突變,交點對應的時刻便是突變開始的時間。按照上述方法,得出花園口水文站年徑流量在1922—1923年度、1993—1994年度可能發生了突變（見圖3)。

圖3 花園口水文站年徑流量Mann-Kendall突變檢驗曲線

2.2.3 滑動t檢驗法

滑動t檢驗法是根據檢驗樣本均值存在的差異是否顯著的方法來檢驗突變的,其基本思想是把時間序列中兩段子序列的均值是否存在顯著差異,看成來自總體的均值有無顯著差異來進行檢驗。如果兩段子序列的均值之間的差異超過了一定的顯著性水平,就可認為有突變發生。

設滑動點前后兩個序列總體的分布函數分別為F1（x)和F2（x),從中分別抽取容量為n1和n2的兩個樣本,檢驗原假設,若F1（x)＝ F2（x),則該抽樣分布函數為

其中

式中：ˉx1、ˉx2分別為前后兩個樣本的均值；、分別為兩個樣本的方差；Sw為兩個樣本方差的線性組合。

T服從t（n1+n2-2)分布,與顯著性水平 α＝0.05時在 t分布表中查得的臨界值 t1-α／2對比,若 ｜T ｜＞t1-α／2,拒絕原假設,則兩子序列存在顯著性差異；反之,兩子序列不存在顯著性差異［12］。本文子序列長度n1和n2取8,選取α＝0.01顯著性水平檢驗變異程度。運用滑動t檢驗法對花園口水文站的年徑流量進行突變分析,檢驗樣本均值存在的差異是否顯著,結果見圖4。由圖4可知,花園口水文站年徑流量在1929—1939年、1968年、1985年、1988—1991年、2002年發生變異,其中1930—1934年、1989—1991年為0.10顯著性水平下的變異點。

2.2.4 突變點檢驗結果及成因分析

對以上3種檢驗法得到的突變點進行匯總,見表2。

表2 年徑流量突變點檢驗結果

由表2可以看出,花園口水文站年徑流量在水文年1933—1934年度、1989—1990年度發生了突變。因此,將花園口的徑流時間序列分為1919—1933年、1934—1989年、1990—2016年3個階段。

徑流形成過程是多重因素相互作用的復雜自然現象。資料顯示,黃河流域1933年發生特大洪水,受災面積超過1萬km2,而1972—1989年黃河連年斷流。20世紀30年代,流域用水規模不大,自然因素起主導作用,1933年突變的主要因素為全球大尺度的降水、氣溫變化；80—90年代用水量激增,流域尺度的小循環使得徑流時間序列發生突變,1989年的突變現象主要為人為因素導致的用水量增加和流域下墊面改變。

2.3 趨勢分析

趨勢分析即分析水文時間序列變化總體的傾向［13］,分析結果一般有增大、減小、不變3種。本文采用線性趨勢回歸檢驗法、Mann-Kendall趨勢檢驗法、Spearman秩次相關檢驗法對花園口水文站徑流量變化趨勢進行分析。

2.3.1 線性趨勢回歸檢驗法

對于檢驗自變量與因變量之間是否存在線性關系,序列xt（t＝1,2,…,n)的線性趨勢成分Yt與時序t的線性回歸方程為

其中a和b的估計式為

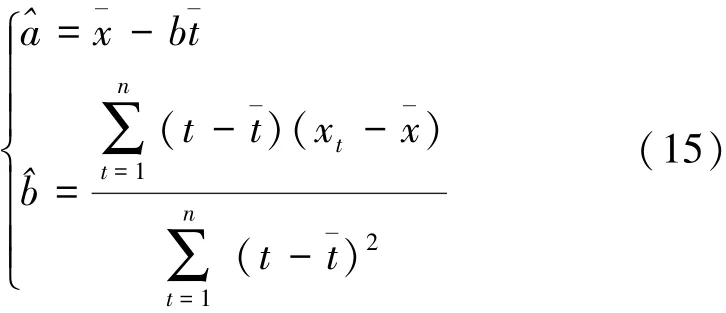
式中：Yt為因變量；a為常數；b為回歸系數；＾a和＾b分別為a和b的估計值；t為時序；ξt為殘差項；ˉx、ˉt分別為xt和t的均值。

構造統計量：

式中：d為服從t分布的函數；為的方差為殘差項平方和與自由度的比值。

式（16)服從自由度為（n-2)的t分布［14］。 假設原序列無趨勢性,按照式（16)～式（19)計算d,選擇顯著水平α＝0.05,在t分布表中查出臨界值與計算的d值比較,當時,拒絕原假設,序列趨勢性顯著。按照上述方法對突變點劃分的3個階段進行線性趨勢回歸檢驗,結果見表3。

表3 年徑流量線性趨勢回歸檢驗結果

由表3可知,數據序列總體變化趨勢較為顯著,通過0.01的顯著性檢驗,其中：1919—1933年變化趨勢相對顯著,通過0.05的顯著性檢驗；1934—1989年、1990—2016年變化趨勢平穩。

2.3.2 Mann-Kendall趨勢檢驗法

運用Mann-Kendall趨勢檢驗法進行趨勢分析時,同樣不要求被分析樣本遵從一定分布,該方法是關于觀測值序列的秩次和時序的秩次相關檢驗,原假設H0為時間序列xt（t＝1,2,…,n)n個獨立的隨機變量同分布的樣本,Mann-Kendall檢驗法中的統計變量S計算公式為

其中

式中：Ri和Rj分別為xj和xi的秩次；n為序列長度。

當n＞8,假設實測數據服從獨立且同分布,統計量S服從正態分布,其均值和方差滿足：

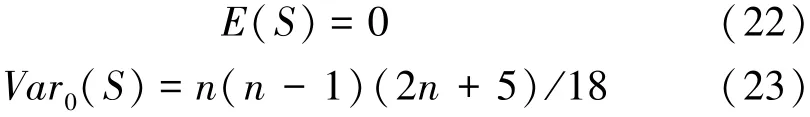
標準正態分布統計量計算式為

在趨勢檢驗中,選擇顯著性水平α＝0.10,當｜Z｜＜時,接受原假設,即趨勢不顯著；反之,則趨勢顯著。統計變量Z＞0時,序列存在上升趨勢；Z＜0時,序列存在下降趨勢。另選取顯著性水平α＝0.05及α＝0.01檢驗趨勢顯著程度。根據上述方法分析花園口水文站年徑流量變化趨勢,結果見表4。

表4 年徑流量Mann-Kendall趨勢檢驗結果

從表4可以看出,數據序列總體趨勢顯著,通過0.05的顯著性檢驗,統計值小于零,總體呈現下降趨勢,其中：1919—1933年變化趨勢相對顯著,通過0.10的顯著性檢驗,表現為下降趨勢；1934—1989年、1990—2016年變化趨勢平穩。

2.3.3 Spearman秩次相關檢驗法

Spearman秩次相關檢驗法是通過分析時間序列xt與其時序t的相關性來檢驗其趨勢性的方法［15］。xt用其秩次Rt（Rt為將xt從大到小排序所對應的序號)代表,秩次相關系數計算式為

式中：dt為變量從大到小排序的序號與變量對應的時序之間的差值,dt＝Rt-t。

秩次Rt與時序t越接近,則dt的值就越小,秩次相關系數r就越大,趨勢性就越顯著。相關系數是否異于0,用t檢驗法,統計量計算式為

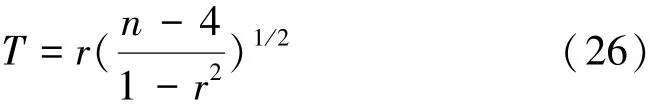
式（26)服從自由度為（n-2)的t分布。假設序列無趨勢,將計算出的T與在t分布表中查得的顯著性水平α＝0.05對應的臨界值則拒絕原假設,序列趨勢顯著；反之,序列趨勢不顯著,另選取顯著性水平α＝0.01檢驗趨勢顯著程度。根據上述方法分析花園口水文站年徑流量變化趨勢,結果見表5。

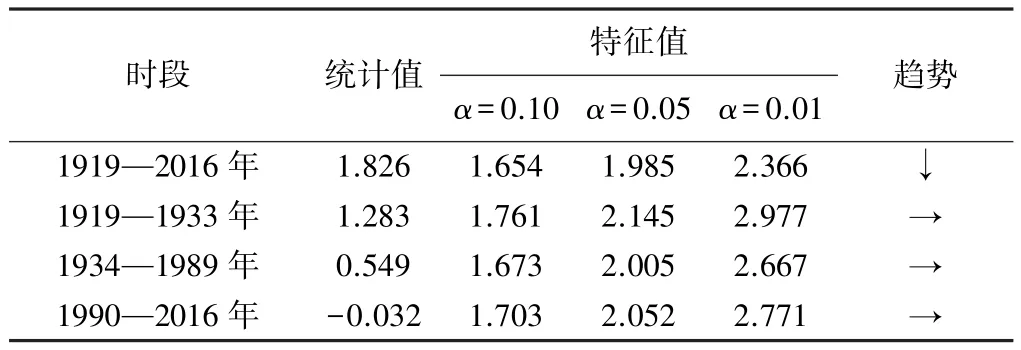
表5 年徑流量Spearman秩次檢驗結果

從表5可以看出,數據序列總體趨勢顯著,通過0.10的顯著性檢驗。根據對突變點劃分的3個階段分析,趨勢表現平穩,均未通過0.10的顯著性檢驗。

2.3.4 趨勢綜合分析

對以上趨勢檢驗分析方法得到的結果進行綜合,假如某種方法檢驗趨勢顯著,則記為“1”,否則記為“-1”,將各種檢驗方法的加和作為徑流時間序列的綜合趨勢（見表6)。

表6 年徑流量各方法檢驗結果

從表6可以看出：總體趨勢較為顯著；1919—1933年減小趨勢顯著,兩種方法的結果均通過0.10的顯著性檢驗；1934—1989年、1990—2016年的趨勢較為平穩。綜合以上分析,花園口年徑流量的突變形式為跳躍突變,1934—1989年的平均年徑流量比1919—1933年增長122億m3,而1990—2016年的平均年徑流量顯著下降,比1934—1989年約減小163億m3（見圖5)。

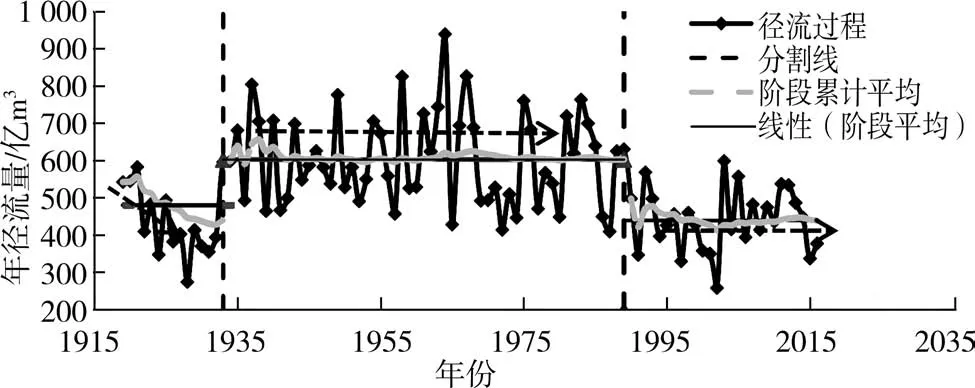
圖5 花園口水文站年徑流量變異前后綜合趨勢檢驗

3 結 論

（1)綜合有序聚類分析法、Mann-Kendall突變檢驗法、滑動t檢驗法分析結果,花園口徑流時間序列在1933—1934年、1989—1990年發生了突變,突變原因前者主要為自然因素（氣溫、降水)大尺度的變化,后者主要為人為因素（用水增加、下墊面改變)流域尺度的變化。

（2)綜合線性趨勢回歸檢驗法、Mann-Kendall趨勢檢驗法、Spearman秩次相關檢驗法分析結果,花園口徑流時間序列在1919—1933年下降趨勢顯著（通過了0.10的顯著性檢驗)；1934—1989年、1990—2016年徑流量變化相對穩定。徑流時間序列的突變類型為跳躍突變,按突變點劃分的3個階段年徑流量平均值相差較大。

黃河流域面積較大,河川徑流的演變比較復雜,在以后的研究中,應結合上中游其他重要水文站,分析黃河不同河段的徑流演變特性。