離散元團聚體法模擬顆粒破碎的參數影響研究

張亞楠，徐 琨，周 偉，馬 剛，賴國偉

(1.武漢大學 水資源與水電工程科學國家重點實驗室，武漢 430072；2.武漢大學 水工巖石力學教育部重點實驗室，武漢 430072；3.長江勘測規劃設計研究院，武漢 430010)

顆粒材料在自然界普遍存在，如砂土、碎石、道砟、堆石體等，因其壓實性良好、抗震性能好、取材便捷等優點，被廣泛用于巖土工程中。由于天然顆粒存在微裂紋等缺陷和材料自身的脆性，承受外界應力時，容易發生破碎[1]。研究表明顆粒破碎對顆粒集合體的力學響應有顯著的影響[2,3]。

顆粒破碎的數值模擬方法為研究裂紋的起裂、發展、貫穿以及從細觀層面研究顆粒破碎機制等方面提供了有效的途徑[4]。目前有多種數值模擬方法可以實現顆粒破碎的模擬，如離散元法(Discrete Element Method,DEM)、連續-離散耦合方法(Combined FDEM)[5-7]等。其中，基于DEM采用顆粒黏結模型(Bonded-particle model，BPM)生成可破碎團聚體是模擬顆粒破碎的一種常用方法，簡稱為團聚體法。

在使用團聚體法開展的顆粒破碎研究方面，Hazzard等[8]通過模擬研究巖性材料破碎過程，發現局部阻尼可以用來模擬顆粒材料對應力波的衰減作用。Thornton等[9]研究了不同堆積狀態的團聚體壓碎過程中黏結鍵演化規律及破碎后碎片特征。Potyondy等[10]系統的提出團聚體法并很好地模擬了巖石破碎過程，探究了子顆粒尺寸、材料強度等參數對材料宏觀力學參數的影響。Lim等[11-12]研究表明團聚體子顆粒數目少于500個會影響顆粒破碎模擬效果；并發現局部阻尼系數對單顆粒峰值破碎強度影響不明顯。Cil等[13]研究了顆粒破碎過程中顆粒裂紋的發生與擴展過程。Wang等[14]則通過物理實驗和道砟顆粒的壓碎數值試驗，分析了結晶尺寸、加載速率等對其宏觀力學參數的影響。

綜上，采用團聚體法模擬顆粒破碎時細觀參數的選取十分重要，但目前針對細觀參數選取對顆粒破碎影響的研究仍不完善，仍需開展進一步研究。為此，本文開展研究分析不同顆粒材料特性對單顆粒破碎的影響及其機理，揭示細觀參數對單顆粒破碎的影響機制，以期為團聚體法參數選取上提供一定參考。

1 單顆粒壓碎數值試驗模擬

1.1 單顆粒壓縮模型制備

本文采用離散元軟件PFC3D通過團聚體法生成可破碎單顆粒(下文統一稱為團聚體)進行單顆粒壓碎的數值試驗。由于本文是為了分析不同細觀參數對單顆粒破碎的影響及其機理，所以排除顆粒形狀的影響，選擇了圓球顆粒作為研究對象。許多學者的研究表明[7-13]，以平行黏結模型PBM(Parelleal-bonded model)可以很好的模擬出巖石材料的多種力學響應特性，因此本文子顆粒之間選取PBM作為團聚體的細觀黏結模型。Potyondy等[9]的研究詳細闡釋了PBM的本構模型，故在此不再贅述。為了模擬天然顆粒材料內部結構的缺陷，如微裂隙、微孔洞等和其分布的隨機性，子顆粒間黏結強度設定Cil等[13]使用的方法，即設定其服從Gauss分布。

單顆粒壓縮數值試驗的加載示意圖見圖1。顆粒放置在上下均為剛性的加載板之間。壓縮時，底部加載板設置為全約束，頂部加載板采用位移控制式加載，模擬準靜態單軸壓縮。

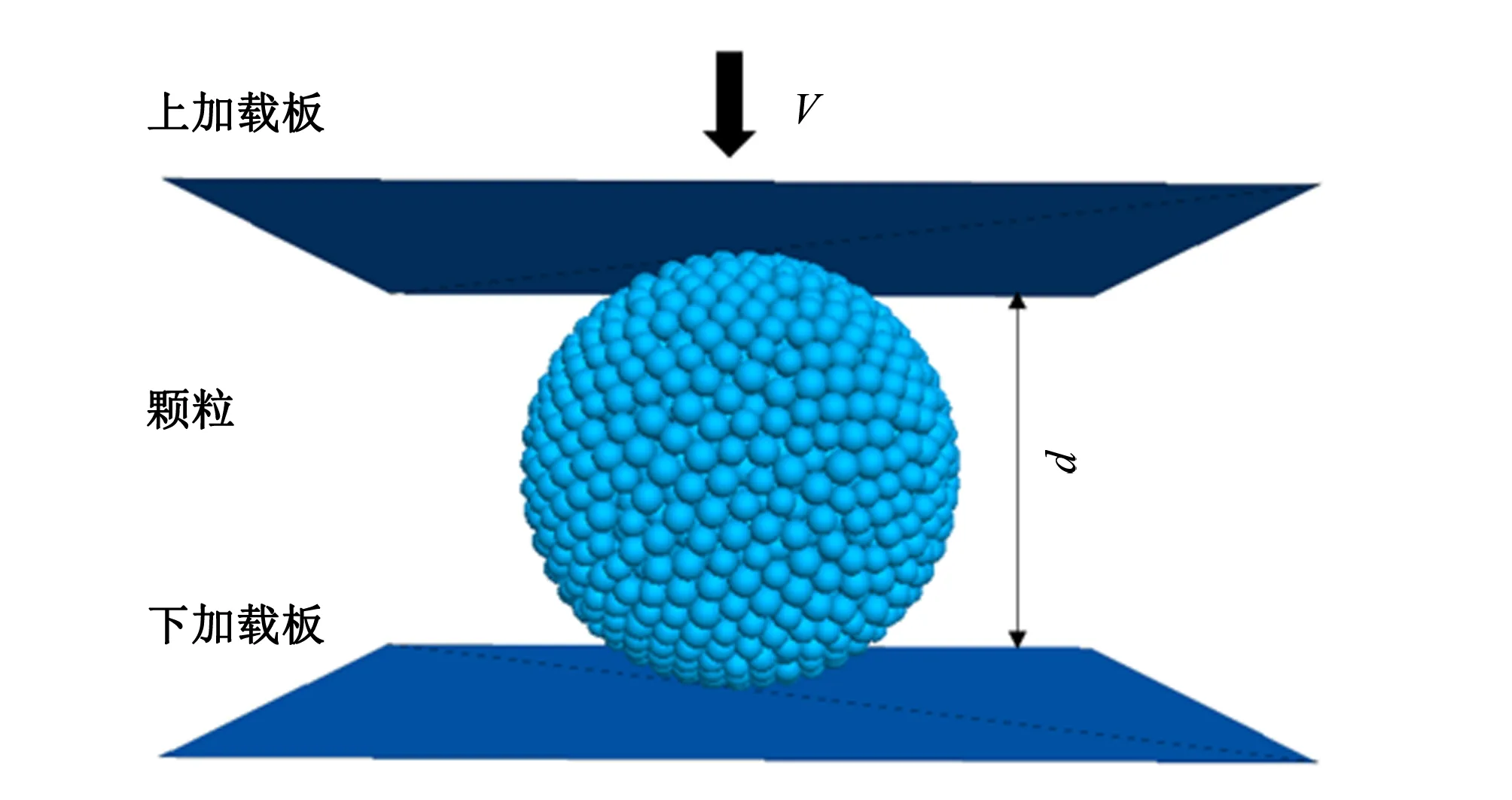
圖1 單顆粒壓縮試驗示意圖Fig.1 Compression test diagram for single particle

1.2 細觀參數取值

團聚體的直徑10 mm，由粒徑在0.3 mm至0.36 mm區間均勻分布的子顆粒黏結而成。生成團聚體過程中，隨機種子數來模擬天然顆粒材料內部空間結構的各異性。參考室內單顆粒壓碎物理試驗[15，17]和離散元數值模擬[8，10]，經過反復試算，本文率定的細觀參數取值如表1所示。試驗中采用符號“SR-1”用來表示第一個單顆粒壓碎數值試驗，其他依次類推。

為實現模擬準靜態加載條件，數值模擬試驗首先進行了一系列加載速度敏感性分析。考慮到滿足準靜態加載條件和較高的計算效率，本次模擬研究最終選定加載速度為0.02 m/s。

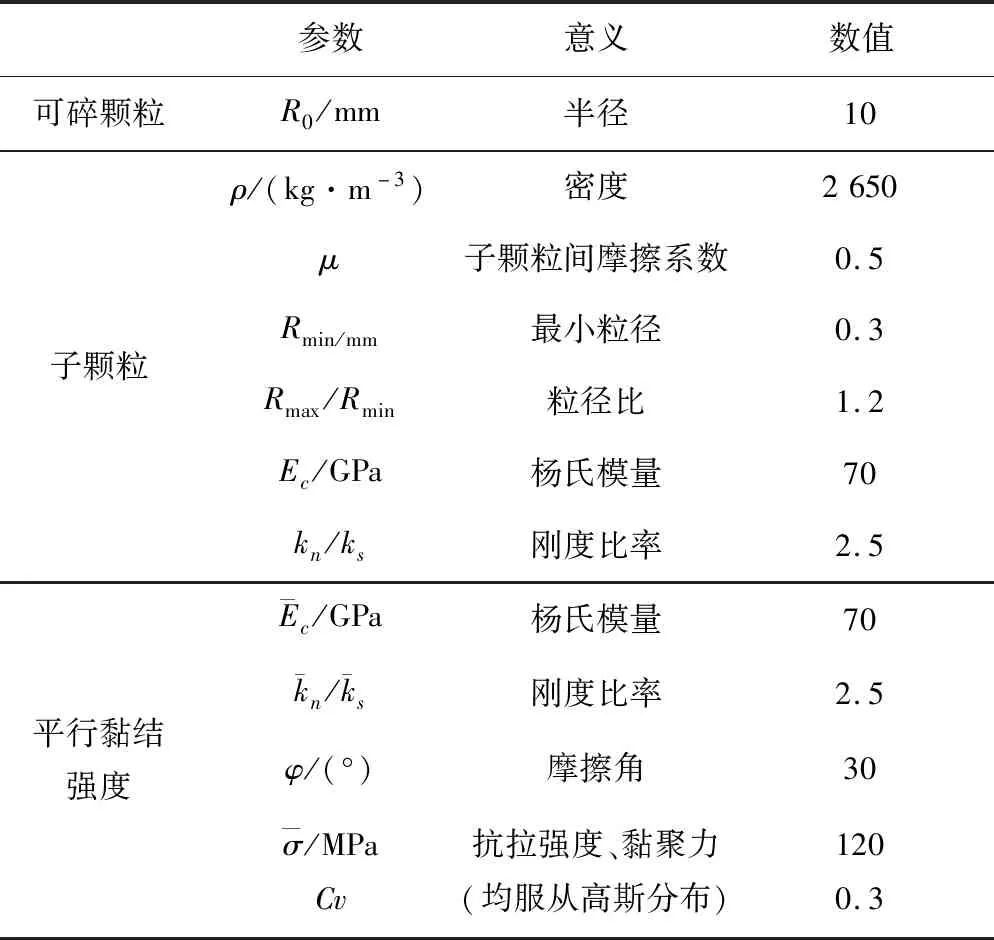
表1 單顆粒壓碎數值試驗參數Tab.1 Input parameters used in the numerical single particle crushing tests

試驗SR-1的力-位移曲線和黏結鍵斷裂累計曲線如圖2所示。數值試驗的力-位移曲線表現出脆性材料破碎的特性，砂子、巖石和玻璃等室內單顆粒壓碎的物理試驗結果[15-17]也定性驗證了數值模擬試驗的力-位移曲線，以上結果表明了本研究中單顆粒壓碎數值模擬試驗的有效性。

圖2 試驗SR-1力位移曲線和黏結鍵斷裂累計曲線圖Fig.2 The force-displacement curve and the evolution of the cumulative broken-bond number of test SR-1

1.3 破碎強度統計分析

單顆粒壓縮試驗作為一種測定顆粒材料抗拉強度的間接方法被廣泛接受。假定測試顆粒的試驗粒徑為d，破碎壓力為F，則測定的抗拉強度σ，即顆粒破碎強度為[18]：

σ=F/d2

(1)

McDowell等[18]通過物理試驗和理論分析驗證脆性材料的抗拉強度分布可以用Weibull分布來描述：

(2)

式中：Ps是對于有限數量壓縮試驗顆粒的累積幸存概率；σ0為顆粒幸存概率為37%時的特征破碎強度；m為Weibull模量，其大小描述了統計的樣本的離散性。

顆粒的生存概率Ps可由下式計算：

(3)

式中：n為壓縮試驗顆粒數；i為顆粒破碎強度按照升序排列所對應的排序號。

若是相同粒徑的顆粒，則d=d0，代入式(2)得：

(4)

對公式(4)兩邊取對數可得：

(5)

由表1模擬參數，生成40個團聚體進行單顆粒壓碎數值試驗，最終得到顆粒峰值破碎強度的數值試驗結果如圖3所示，其中Weibull分布最優擬合線根據式(5)擬合得到。由圖可知，數值模擬結果再現了Huang等[17]和Lobo-Guerrero[20]等室內單顆粒壓碎物理試驗中顆粒破碎強度的Weibull分布特性，進一步驗證了本文數值模擬試驗的有效性。

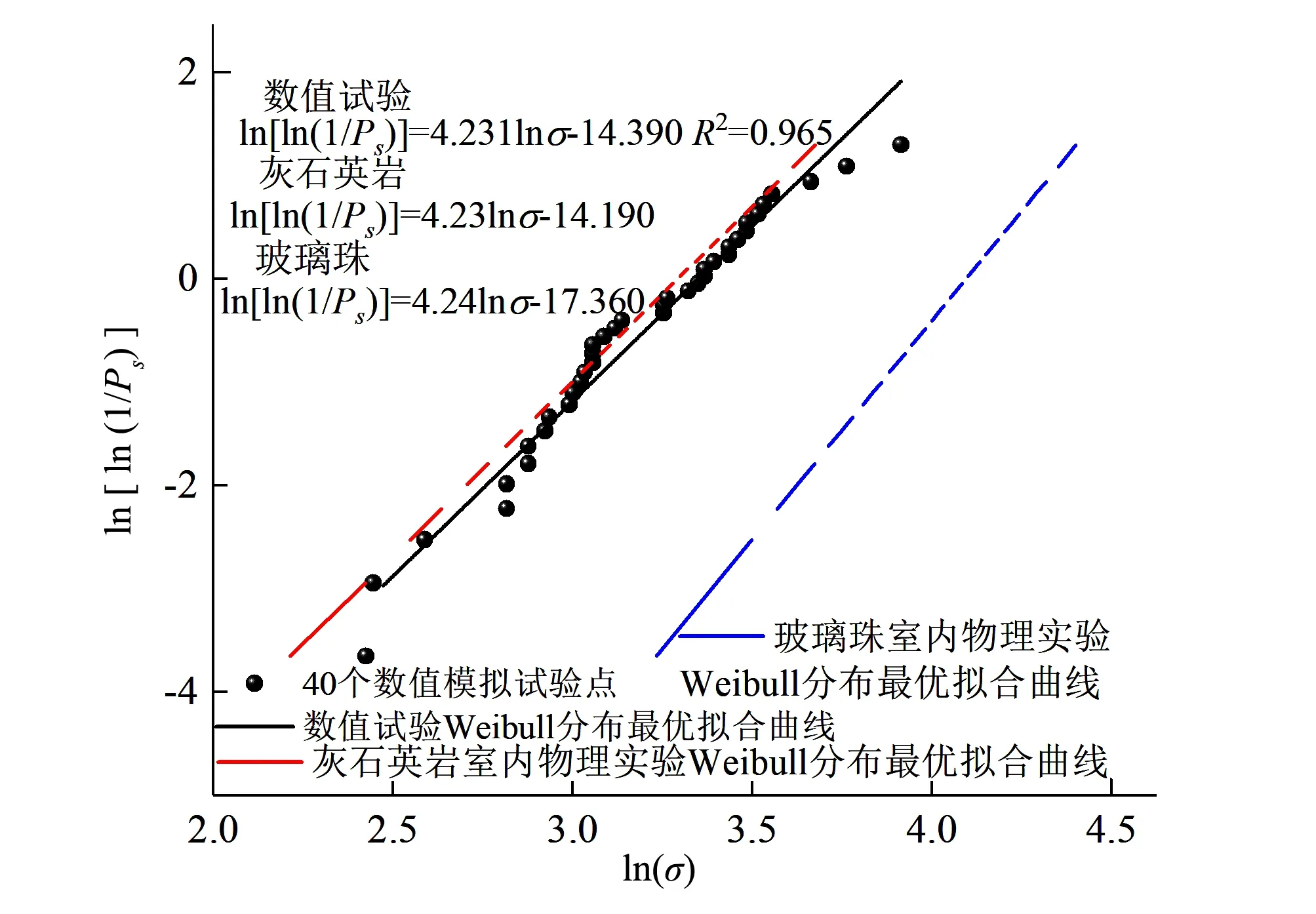
圖3 顆粒破碎強度的數值試驗結果及Weibull擬合線Fig.3 Numerical simulation results for particles with crushing strength and Weibull fitted line

2 細觀參數對單顆粒破碎影響研究

2.1 最小子顆粒尺寸敏感性分析

子顆粒尺寸會改變團聚體中子顆粒的數目，進而影響團聚體的結構，并對團聚體的峰值破碎強度產生影響。Wang等[13]研究表明隨著最小子顆粒尺寸的增加，團聚體的峰值破碎強度會隨之增加。為探究最小子顆粒尺寸對團聚體峰值破碎強度的影響，本節數值試驗中保持表1中其他參數不變，通過調整最小子顆粒粒徑從團聚體直徑(Rmin/R0)的1/25(0.2 mm)至2/25(0.4 mm)，間隔1/100(0.05 mm)，共五組，每組進行10次平行試驗開展研究，最終得到的團聚體峰值破碎強度隨最小子顆粒尺寸變化的關系如圖2所示。由圖可知，各組團聚體峰值破碎強度差異和破碎強度值均呈現出隨最小子顆粒尺寸的增大而增加的趨勢。團聚體子顆粒數目隨最小顆粒尺寸的減少而急劇增加。

考慮到團聚體破碎是由一定數量黏結鍵斷裂導致的，而子顆粒平均配位數則能反映子顆粒上黏結鍵的情況，配位數越大則表明子顆粒間的黏結鍵越多，相同黏結強度情況下團聚體越不易被破壞。提取各組團聚體的子顆粒平均配位數隨最小子顆粒粒徑變化的關系如圖4所示。由圖4可知，子顆粒平均配位數隨最小子顆粒粒徑的增加而增大，與團聚體峰值破碎強度表現出的規律一致。以上研究表明，最小子顆粒粒徑變化引起的團聚體峰值破碎強度的改變是由于子顆粒平均配位數改變引起的。

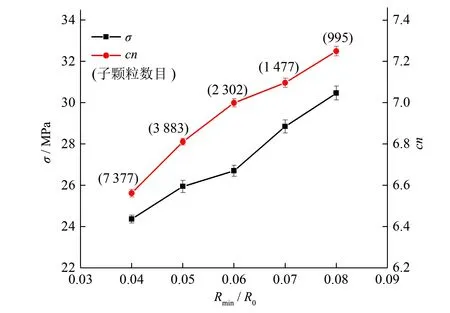
圖4 峰值破碎強度及平均配位數與最小子顆粒尺寸關系Fig.4 Relationship between the particle crushing strength and average coordination number with the minimum radius of sub-particles

2.2 子顆粒黏結強度敏感性分析

子顆粒黏結強度可以表征顆粒材料強度，為探究顆粒材料強度對團聚體峰值破碎強度的影響，本節數值試驗中保持其他參數不變，選取5組子顆粒黏結強度開展研究，即從100 MPa到140 MPa，間隔為10 MPa。團聚體峰值強度隨子顆粒間黏結強度的關系如圖5所示。由圖5可知，材料強度對團聚體的宏觀力學特性影響顯著，顆粒峰值破碎強度隨子顆粒間黏結強度的增加呈線性增長趨勢。子顆粒間黏結強度越高，子顆粒之間黏結鍵越不易發生破壞，宏觀層面上單顆粒達到破碎狀態所需的作用力也越大，因此，隨著子顆粒間黏結強度的增大，團聚體峰值破碎強度也隨之增大。

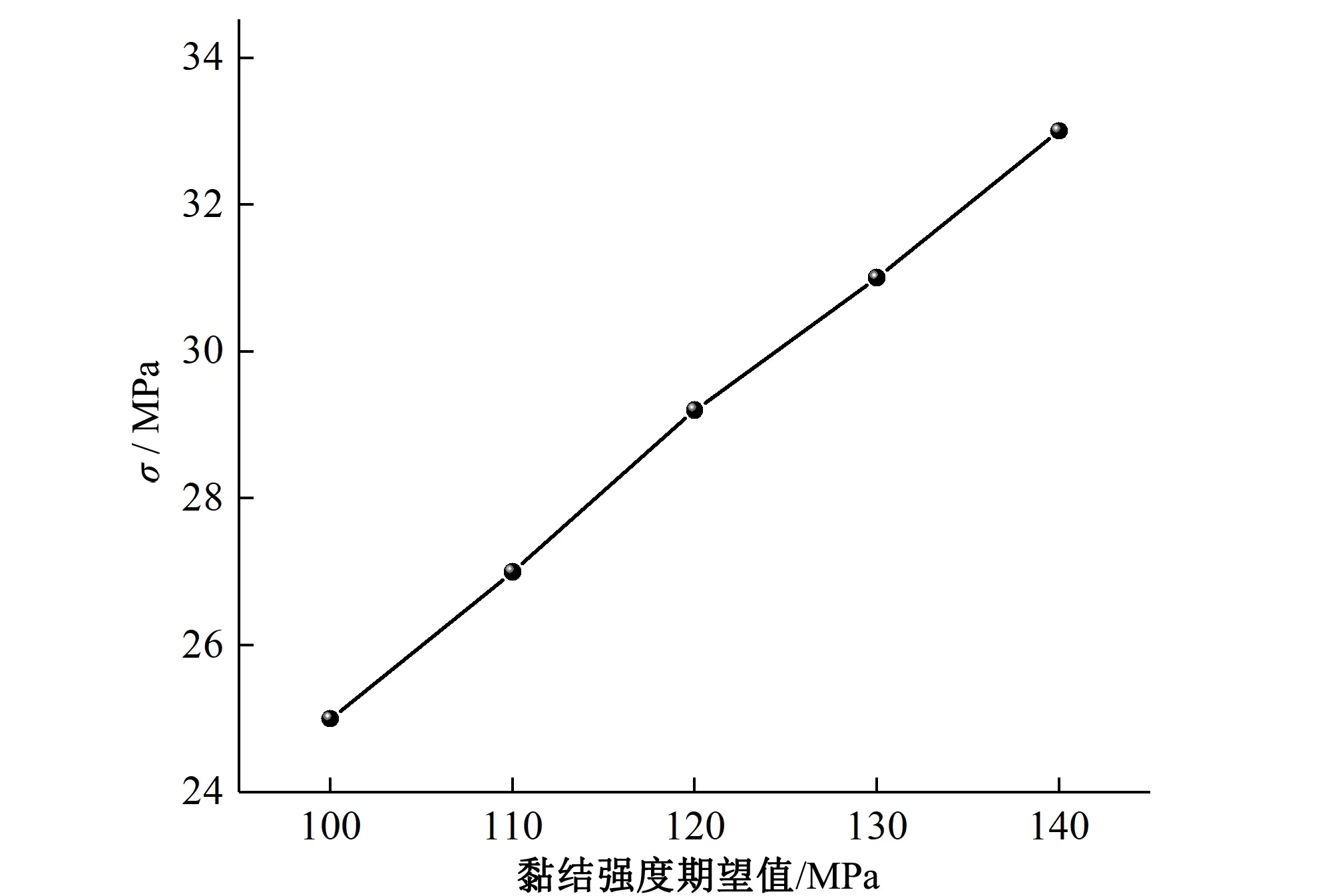
圖5 顆粒峰值破碎強度與黏結強度的關系Fig.5 Relationship between the particle crushing strength and bond strength

2.3 子顆粒間摩擦系數敏感性分析

為探究子顆粒摩擦系數的選取對團聚體峰值破碎強度的影響，本節數值試驗中保持表1中其他參數不變，選取子顆粒間摩擦系數(μ)0.1至0.8，間隔0.1，共8組，每組進行10次平行試驗開展研究。

不同摩擦系數時，團聚體的力-位移曲線如圖6所示。由圖6可知，隨著摩擦系數的增大，力-位移曲線峰前整體有所抬升，且達到峰值時的加載位移隨之增加，但力-位移曲線整體表現出相似形態。

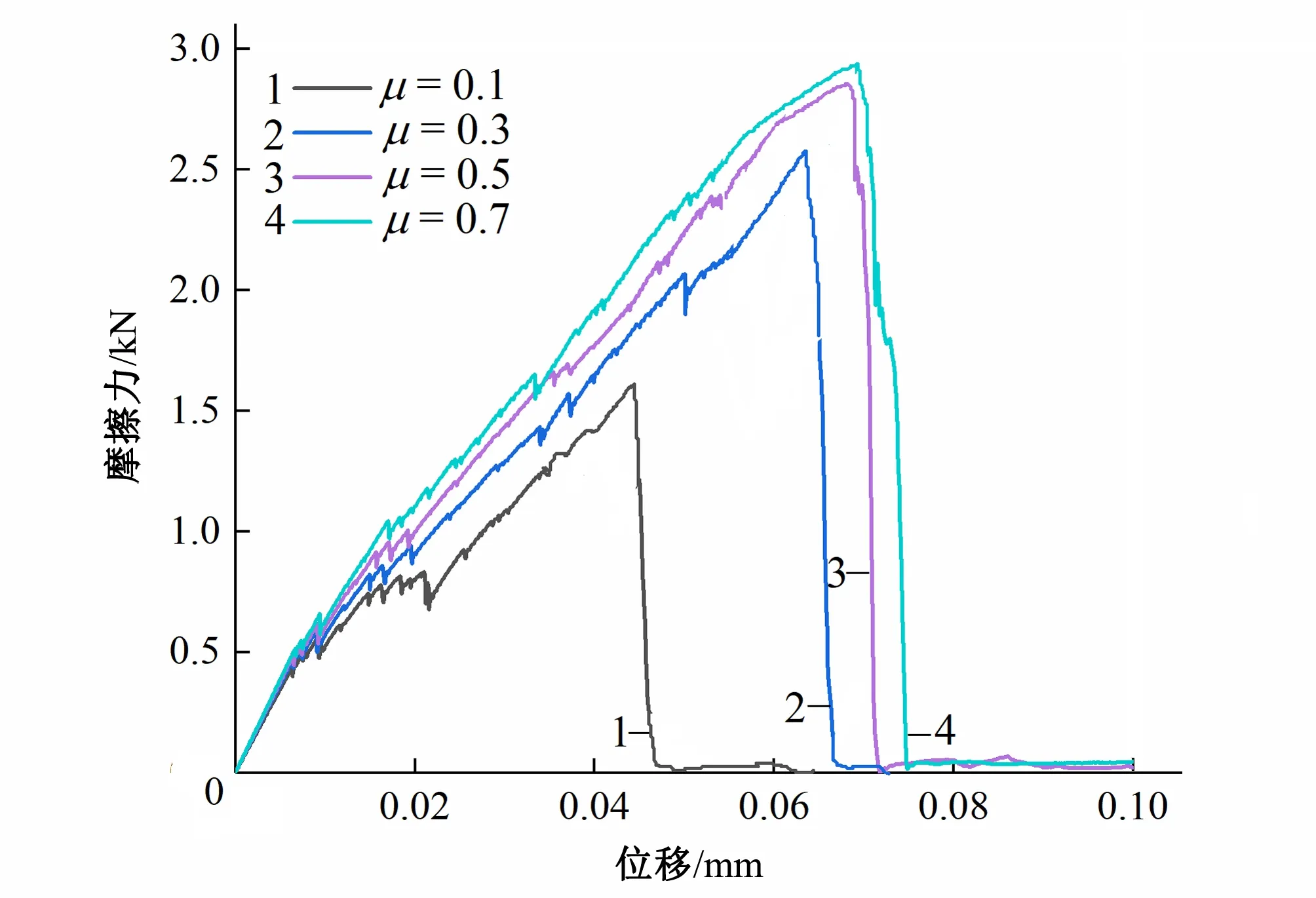
圖6 不同子顆粒摩擦系數的力-位移曲線Fig.6 The force-displacement curve of different friction coefficient between sub-particles

團聚體峰值破碎強度與子顆粒間摩擦系數的關系如圖7所示。由圖7可知，子顆粒間摩擦系數取值較小時，組內團聚體峰值破碎強度差異較大，隨其增加，團聚體峰值破碎強度呈現先急劇增大，然后增速減緩，最后趨于穩定的現象。這是由于子顆粒間摩擦系數增加時，子顆粒間抗滑阻力增大，子顆粒間的黏結鍵越難發生剪切破壞，增強了團聚體整體的承載能力，從而有團聚體峰值破碎強度呈現隨之增大的趨勢。由于顆粒間的黏結鍵也會發生拉伸破壞，黏結鍵發生不同破壞數目占總黏結鍵比率隨子顆粒間摩擦系數變化的曲線如圖7所示，由圖可知，當子顆粒間摩擦系數增大到一定值時，黏結鍵破壞形式中拉伸破壞占主導，因此有團聚體峰值破碎強度在后期增長速率減小，逐漸穩定的現象。

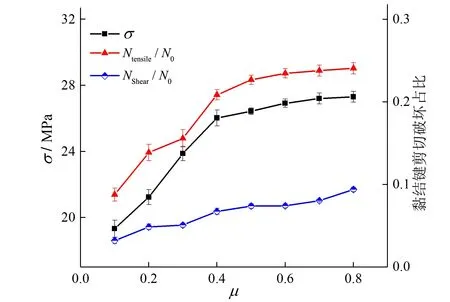
圖7 顆粒峰值破碎強度及黏結鍵剪切、拉伸破壞占比與子顆粒摩擦系數的關系Fig.7 Relationship between the particle crushing strength,the ratio of tensile broken bonds with changing friction coefficient of sub-particles

2.4 局部阻尼系數敏感性分析

顆粒材料在力的作用下形成裂紋時會因能量的快速釋放而產生瞬態彈性波[21]。Hazzard等[8]研究認為顆粒黏結鍵斷裂能夠很好地模擬這種現象，同時局部阻尼可以用來表征顆粒材料對波的衰減作用。Lim等[10]在研究中認為局部阻尼系數可能對顆粒破碎后的碎片尺寸分布有較大的影響，但未進行深入研究。為此本節數值試驗中保持表1中其他參數不變，選取0.1至0.9，間隔0.2，共5組局部阻尼系數(δ)，每組進行30次平行試驗研究局部阻尼系數的改變對單顆粒碎片尺寸分布的影響。各組的峰值破碎強度及其最優Weibull分布擬合線如圖8所示。

圖8 不同局部阻尼系數顆粒破碎強度的Weibull統計圖Fig.8 Weibull survival probability plot for particle with different local damping coefficients

圖9所示為擬合得到的Weibull模量和顆粒特征破碎強度隨局部阻尼系數的變化關系。由圖9可知，局部阻尼系數對Weibull模量有一定的影響，隨其增加而呈增大的趨勢，表明高局部阻尼系數時，團聚體的峰值破碎強度離散程度較小。顆粒特征破碎強度則呈現隨著局部阻尼系數增加而增大，增長趨勢逐漸減緩。

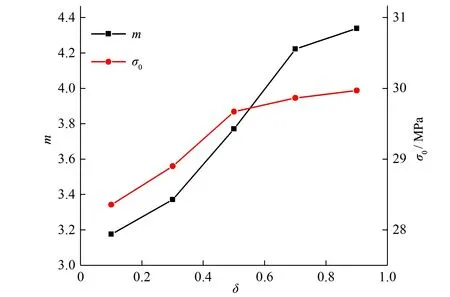
圖9 不同局部阻尼系數的Weibull模量和特征破碎強度Fig.9 Weibull modules and characteristic stresses of particles with different local damping coefficients

圖10所示為局部阻尼系數分別為0.1和0.9的團聚體破碎過程中黏結鍵破壞的空間分布圖(圖中透明藍色表示團聚體，深藍色薄片標志黏結鍵發生剪切破壞，綠色薄片標志黏結鍵發生拉伸破壞)由圖可知，低局部阻尼系數時，團聚體由于黏結鍵斷裂形成的應力波會引起其周圍的黏結鍵產生較大的應力波動，從而導致更多的黏結鍵破壞，最終造成團聚體較早破碎；而高局部阻尼系數時，團聚體中黏結鍵斷裂產生的應力波傳播范圍小，波動也有所降低，相鄰的黏結鍵狀態相互影響程度被削弱。因此低阻尼系數團聚體破壞較早且峰值破碎強度略低。

圖10 不同局部阻尼系數顆粒破碎過程Fig.10 Fracture process of particles with different local damping coefficients

為研究局部阻尼系數對單顆粒破碎后碎片尺寸分布的影響，分別提取出各組中每個顆粒破碎后的碎片尺寸，按各顆粒碎片尺寸的大小排序得到前兩個碎片質量百分比分布如圖11所示。由圖可知，各組單顆粒的碎片尺寸分布的規律基本相似。隨著局部阻尼系數的增加，試驗組中出現較大尺寸的最大碎片的比例有降低趨勢；相反的，試驗組中出現較大尺寸的第二大碎片的比例有升高趨勢，以及圖中的最大碎片與第二大碎片的分布有收攏趨勢。從整體來看，低阻尼系數下，各組顆粒破碎后的最大碎片尺寸差異明顯；隨著局部阻尼系數增加，顆粒破碎后各試樣組大碎片的尺寸分布差異逐漸變小。

圖11 不同局部阻尼系數碎片尺寸排位前二的質量分布圖Fig.11 First two fragments mass distributions with different local damping coefficients sorted by the largest fragment mass

試驗后團聚體黏結鍵斷裂位置的空間分布如圖12所示。由圖12，結合圖10可知，加載過程中，往往是團聚體與加載板相接觸部位最先發生黏結鍵斷裂，黏結鍵斷裂產生的應力波誘發附近的黏結鍵發生破壞。低局部阻尼系數時，黏結鍵斷裂產生的應力波削減程度小，周邊黏結鍵受應力波影響較大，易發生破壞，從而造成接觸部位附近的黏結鍵失效較多，團聚體易在接觸部位發生破壞，最終團聚體破碎后碎片尺寸差異較大；而高局部阻尼系數時，黏結鍵斷裂產生的應力波被極大的削弱，黏結鍵斷裂產生的應力波不足以使周邊黏結鍵發生斷裂，破壞大多沿加載徑向發生，從而產生徑向劈裂，最終團聚體破碎后形成的大尺寸碎片的尺寸差異較小。

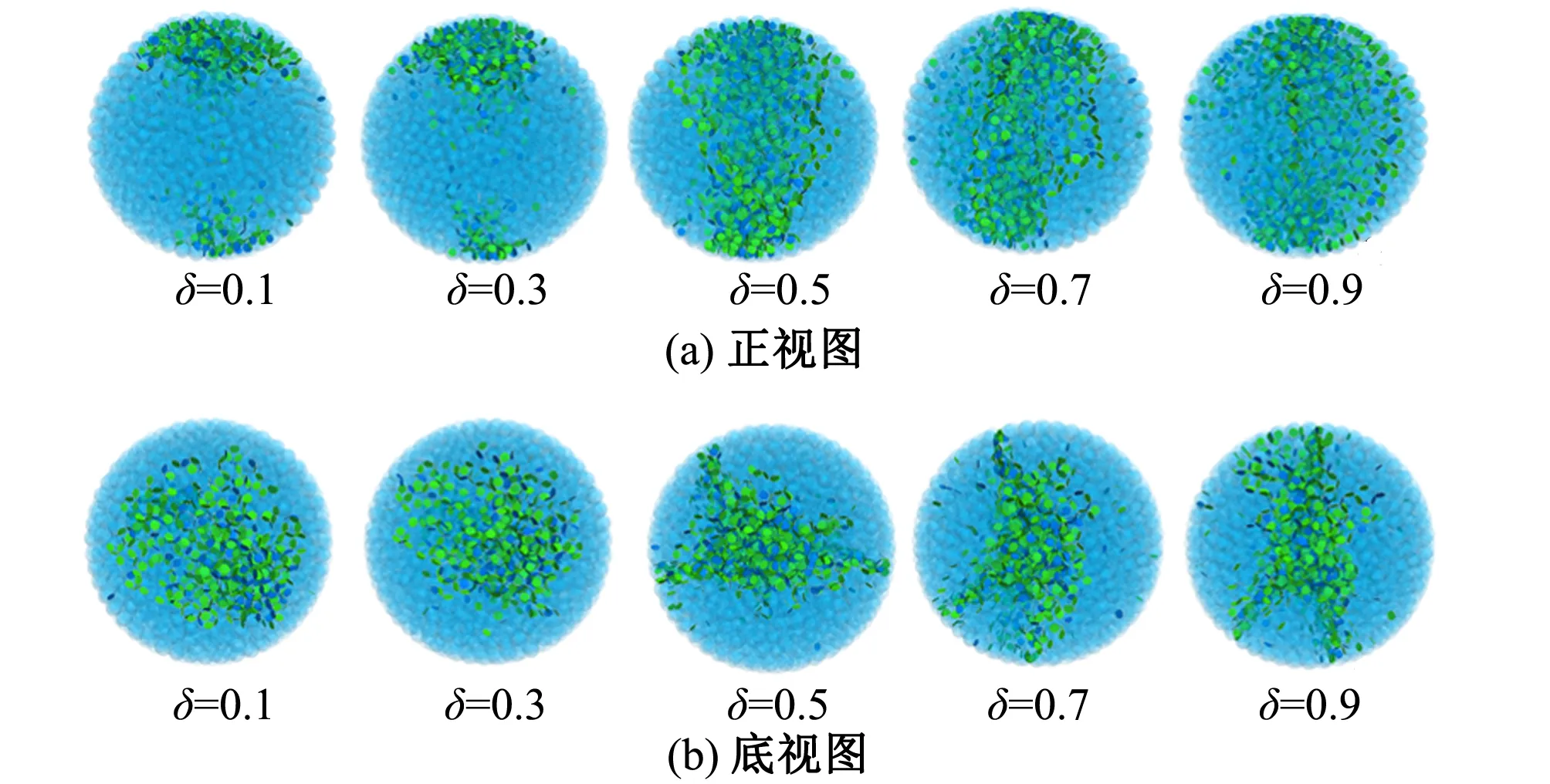
圖12 不同局部阻尼系數下顆粒黏結鍵斷裂的空間分布圖Fig.12 Spatial distribution of broken particle bonds with different local damping coefficients

綜上所述，局部阻尼系數對單顆粒統計特征破碎強度和其離散性影響較小，但會對顆粒材料斷裂后應力重分布存在影響，其值大小可以體現不同顆粒材料對開裂后形成應力波的衰減作用，對顆粒材料破碎后的碎片形態和破碎機制影響較大。

3 結 論

本文采用團聚體法模擬單顆粒破碎過程，通過一系列單顆粒壓碎數值試驗對影響材料特性的細觀參數開展敏感性分析，詳細研究了最小子顆粒尺寸、子顆粒間黏結強度、子顆粒間摩擦系數以及局部阻尼系數對顆粒破碎宏觀力學性能的影響和細觀機制，得出如下結論：

(1)最小子顆粒尺寸越大，則團聚體平均配位數增加，從而子顆粒間的黏結更為緊密，最終表現出單顆粒峰值破碎強度的增加。

(2)子顆粒間黏結強度對單顆粒峰值破碎強度的影響顯著，隨其增加呈線性增長趨勢。

(3)子顆粒間摩擦系數增加會抑制顆粒發生剪切破壞，從而提高顆粒的承載力；后隨其增大，拉伸破壞占主導，故單顆粒峰值破碎強度呈先急劇增大，后增速減緩，最后趨于穩定。

(4)局部阻尼系數可以削弱黏結鍵破壞產生的應力波的傳遞，對顆粒破碎機理和碎片尺寸分布有著顯著的影響。局部阻尼系數較小時，顆粒易在接觸部位發生破壞，最終顆粒破碎后碎片尺寸差異較大；局部阻尼系數較大時，顆粒大多產生徑向劈裂，破碎后形成的碎片尺寸差異較小。

(5)單顆粒峰值破碎強度隨上述細觀參數數值的增加均呈現增長趨勢，其中子顆粒間黏結強度即顆粒材料強度改變對其影響最為顯著；其次是最小子顆粒尺寸改變顆粒的內部結構而產生影響；再者是子顆粒間摩擦系數增強顆粒材料內部咬合力而提高顆粒承載力；局部阻尼系數對其影響最小，但其能表征材料抑制應力波傳遞，故對顆粒破碎機理和碎片尺寸分布影響顯著。