緊致交錯網格優化差分系數二維聲波方程數值模擬

汪 勇 王 鵬 蔡文杰 桂志先

(油氣資源與勘探技術教育部重點實驗室(長江大學)，湖北武漢 430100)

0 引言

地震波場數值模擬是應用數值方法模擬地震波在地下介質中的傳播過程，得到在地面或地下各觀測點地震記錄的一種方法，是地球物理勘探和地震學的重要基礎。隨著有限差分數值模擬技術的發展，針對實際應用中提高有限差分計算效率[1]、模擬精度[2]、算法穩定性[3-4]，處理復雜介質[5-7]、吸收邊界條件[8-10]和壓制數值頻散[11-13]等多方面需求，已研發了多種實用技術，并取得相應研究成果。

提高差分格式數值計算精度最直接的方法就是在模擬時增加(加密)網格節點數，但隨之也增加了運算量和存儲空間。緊致差分方法能較好地解決這個矛盾； 同時緊致差分是一種隱式差分格式，穩定性較強。這些優勢使其成為目前頗受關注的有限差分方法之一，并被廣泛應用于聲波、彈性波和復雜介質等地震波場數值模擬中[14-22]，提高了地震波場數值模擬的精度和計算效率。

而Madariaga[23]提出的交錯網格差分格式既可提高數值模擬的局部精度，還能加快收斂速度。將交錯網格與緊致差分技術結合，可進一步提高數值模擬的精度和壓制數值頻散的能力[24-26]。

為使差分格式在較大波數范圍內減少頻散誤差，Kim等[27]基于頻散關系保持(Dispersion relation preserving，DRP)的思路優化了緊致差分格式，指明采用這種優化差分系數方法可使差分算子最大程度地逼近空間偏導數算子。Liu等[28]基于頻散關系提出了優化的時空域有限差分系數，在不增加計算成本的情況下可顯著提高模擬精度。Zhang等[29-30]應用最大范數的目標函數及模擬退火算法求解目標函數，優化了一階和二階常規中心差分格式的差分系數。Liu[31-32]利用最小平方法優化了二階導數中心差分和一階導數交錯差分系數。Yu等[33]基于DRP思想，優化得到5階精度的組合型緊致差分系數。Ren等[34]以優化后時空域差分格式進行聲波和彈性波方程的數值模擬。Yang等[35-36]利用極值逼近(Minimax approximation)算法優化了交錯網格差分系數，當波數較大時可提高模擬精度。

本文首先討論了一階導數的2N階緊致交錯差分格式的建立方法； 基于頻散關系保持的思想，通過最小平方法建立了最小數值波數誤差的目標函數，利用拉格朗日乘數法求解目標函數，得到優化后的4～10階精度差分系數； 然后分析和對比優化前、后的緊致交錯網格差分格式的模擬精度、數值頻散和聲波方程的穩定性條件，并用優化后的緊致交錯差分格式對一階速度—應力聲波方程組進行數值模擬。研究結果表明，采用優化差分算子能有效壓制數值頻散，提高差分近似導數的精度。

1 二維聲波方程的高階差分近似

Madariaga[23]早年提出的波動方程交錯網格數值模擬方法的差分精度為O(Δt2+Δx2)； Levander[37]應用交錯網格方法求解P-SV波方程，將差分精度提高到O(Δt2+Δx4)； 董良國等[3]提出了一階彈性波方程交錯網格高階差分解法，其差分精度達到O(Δt2M+Δx2N)。現今，交錯網格有限差分方法已成為一種高效且應用廣泛的數值模擬方法。

根據彈性力學分析，二維情況下一階應力—速度聲波方程組(假設體力為零)可表示為

(1)

式中：P為應力(標量)；Vx和Vz分別表示x和z方向質點振動速度分量；ρ為介質密度；v為地震波速度。

1.1 時間2M階近似

用交錯網格法進行聲波方程數值模擬時，速度和應力分量分別是在t和t+Δt/2時刻計算的，其中Δt為時間步長。用泰勒公式可得速度分量Vx的2M階精度時間遞推式

(2)

當M=1時，即可得到時間二階精度差分近似

(3)

同理可得速度分量Vz和應力分量P的時間二階精度差分近似

(4)

(5)

利用應力—速度方程組，將式(3)～式(5)中的變量對時間的導數轉換為對空間的導數，則可得

(6)

1.2 空間2N階緊致交錯差分近似

緊致交錯差分格式最早由Nagarajan等[38]提出，用于大渦模擬(Large eddy simulation)問題，該差分格式利用4個網格節點可得到6階空間精度。隨后，Boersma[39]提出最高可達12階空間精度的緊致交錯差分格式，用于可壓縮流體的Navier-Stokes方程的數值模擬。類似于常規交錯網格數值模擬，緊致交錯網格法求取變量的導數時，也是在相應的變量網格點之間的半程上進行的。

一階導數的2N階精度緊致交錯差分格式為

(7)

式中：h為空間網格尺寸；a和bn是差分系數。利用式(7)近似計算式(6)中變量對空間的一階導數，確保2N階差分精度的關鍵是確定差分系數a和bn。利用泰勒級數展開和待定系數法，即用

(8)

可求得緊致交錯網格2N階空間差分精度的差分系數。如當差分精度2N=10時，上述方程組共有5個方程，可確定a和bn(n=1～4)共5個差分系數。

此外，從上述公式可看出，常規交錯差分格式(Staggered finite difference，SD)求取中心點處的導數值時，僅用到周圍網格點的函數值，而緊致交錯差分格式(Staggered compact finite difference，SCD)卻還用到相鄰點導數值。緊致交錯網格法只需利用2N-2個節點即可達到2N階空間差分精度，而常規交錯網格法則須使用2N個節點，因此SCD方法可節省存儲空間。表1列出4～10階泰勒級數展開得到的差分系數。

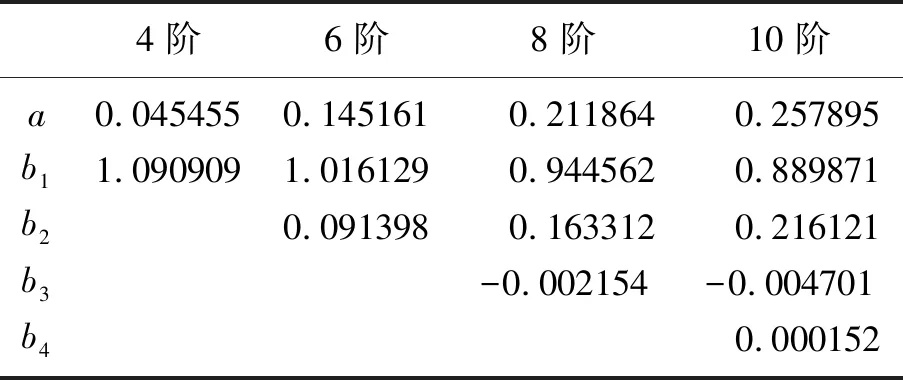
表1 緊致交錯差分格式一階導數的差分系數

1.3 差分格式的矩陣形式

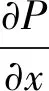
(9)

其中

向前差分為

向后差分為

據式(9)，由應力(標量)場P求取其空間一階導數

(10)

上述各式中差分系數a和bn(n=1～4)由表1給出，可求得一階導數的4～10階空間差分精度近似值。

2 緊致交錯格式差分系數優化及分析

在地震波場數值模擬中，為得到清晰的波場記錄，需要高精度的空間離散差分算子。差分算子的精度取決于差分系數和差分階數，差分階數越高，差分算子越精確，但其運算量也會隨之增加。優化差分系數可使差分算子最大程度地逼近空間偏導數算子，本節對一階導數的緊致交錯差分系數進行優化，進一步提高緊致交錯差分格式的分辨率，并分析優化后的差分格式的精度、頻散和穩定性。

2.1 優化差分系數

首先對一階導數的緊致交錯差分格式(式(7))進行數值頻散分析。令

(11)

式中：h為網格尺寸；k為真波數。若數值模擬時不存在誤差，則B=(ik)A。但在差分計算中，可能會產生不同結果，即產生數值波數(又稱修正波數)。可令B=(ik′)A,k′為修正波數。

將式(11)代入式(7)，并用歐拉公式化簡可得

(12)

式中：ω=kh;ω′=k′h。

在理想情況下，若不存在數值頻散，則ω′=ω。它們的差異越大，說明該方法的數值頻散越嚴重；反之則說明該方法能更好地壓制數值頻散。依據修正波數盡可能在大范圍內接近真波數，以4點緊致交錯差分格式為例說明優化的思路和方法。

由式(7)可得

(13)

為了滿足2階和4階精度泰勒公式截斷誤差的要求，式中差分系數a、b1和b2須滿足下列方程組

(14)

即為式(8)表示的前兩個方程。

為了確定上述方程中的未知差分系數，按照Tam等[40]的思路和方法，在某個選定波數范圍內，確定式(13)中3個未知差分系數，使得修正波數盡可能地接近真波數，故定義誤差函數為

(15)

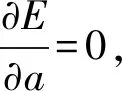
(16)

其中

(17)

由式(14)和式(16)中的3個方程，可確定3個優化后差分系數，即a=0.185715、b1=0.985714、b2=0.128572。將優化后的差分系數代入式(13)，則得到優化后的緊致交錯差分格式(Optimized staggered compact finite difference，OSCD)。

需要說明的是： 4階精度OSCD格式在式(14)基礎上，需加入一個表示DRP要求的積分方程，所以不能嚴格滿足空間6階精度泰勒公式截斷誤差的要求，只能達到空間4階精度近似； 而常規SCD格式的3個方程即能滿足空間6階精度截斷誤差的要求。因此，若要達到2N階空間差分精度，SCD方法只需利用2N-2個節點，而OSCD方法需使用2N個節點，與SD方法使用的節點數相同。

采用同樣方法，對式(7)表示的6～10階OSCD格式做差分系數優化，優化后差分系數列于表2。

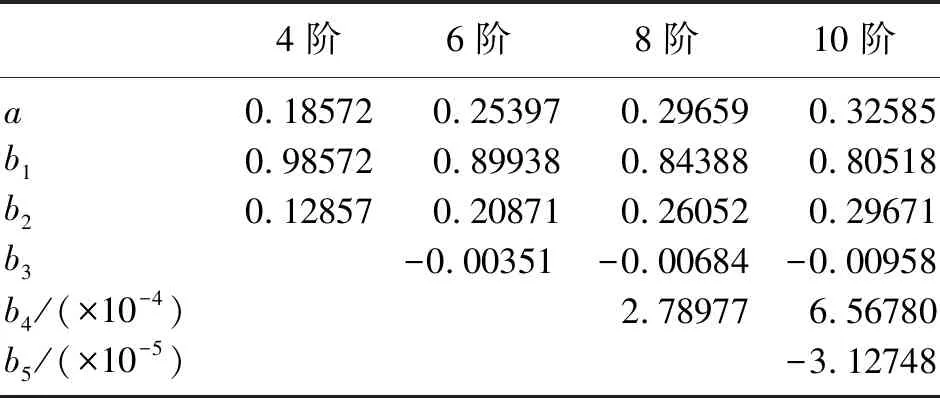
表2 優化的緊致交錯網格一階導數的差分系數

本文方法與文獻[33]方法基本一樣，不同之處在于： 文獻中原差分格式是3點6階組合型緊致差分格式，為了加入代表DRP思路的積分方程，在原差分格式基礎上構造了新格式，增加了1個網格節點，降低了1階精度，得到的是4點5階迎風型組合緊致差分格式； 本文的優化格式與原緊致交錯差分格式相比，在使用同樣網格節點進行差分計算時，降低了2階精度。

本文求取優化差分系數的方法本質上是根據泰勒級數展開式，而文獻[35]和[36]則是根據函數逼近的思路。文獻[35]首先根據緊致交錯差分格式的頻散關系和極小極大原則建立了誤差函數，在所有逼近格式中尋找誤差最小且滿足誤差標準的三角函數多項式，求取過程中使用的是列梅茲(Remez)迭代算法。文獻[35]指出該方法求得的差分系數在中等和大波數條件下比泰勒級數得到的要好，但算法復雜，實現難度較大，這也限制了該方法的應用。此外，該方法得到的差分格式是在給定的誤差標準條件下得到的，但不能明確差分格式的近似精度，即通常意義上的2N階。

2.2 頻散分析

對優化前、后一階導數的緊致交錯差分格式進行數值頻散分析，通過數值波數與真波數的比值評判優化效果并確定適用的空間網格尺寸。

據式(12)，修正波數與真波數之比可定義為

(18)

在理想情況下，若不存在數值頻散則波數比R恒等于1。R偏離1越大，說明該方法的數值頻散越嚴重； 反之則說明該方法能較好地壓制數值頻散。利用表1和表2中不同精度的差分系數可求取優化前后的波數比曲線。為了比較，計算得到常規交錯差分格式(SD)的波數比，計算公式見文獻[35]，不再贅述公式。

圖1為3種差分格式在不同差分網格節點個數(即差分算子長度)情況下的波數比曲線，如圖1a為4個差分節點，根據前文分析，SD、SCD和OSCD格式分別可達到4階、6階和4階差分精度。

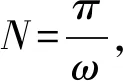
此外，從圖中可見：低階差分精度時，三者波數比曲線差別最大； 隨差分精度增加，差異變小。顯然，OSCD格式在壓制數值頻散方面的優勢主要體現在低階差分精度時。因此，可用較低(4或6)階OSCD格式達到高階SCD或SD格式的效果。

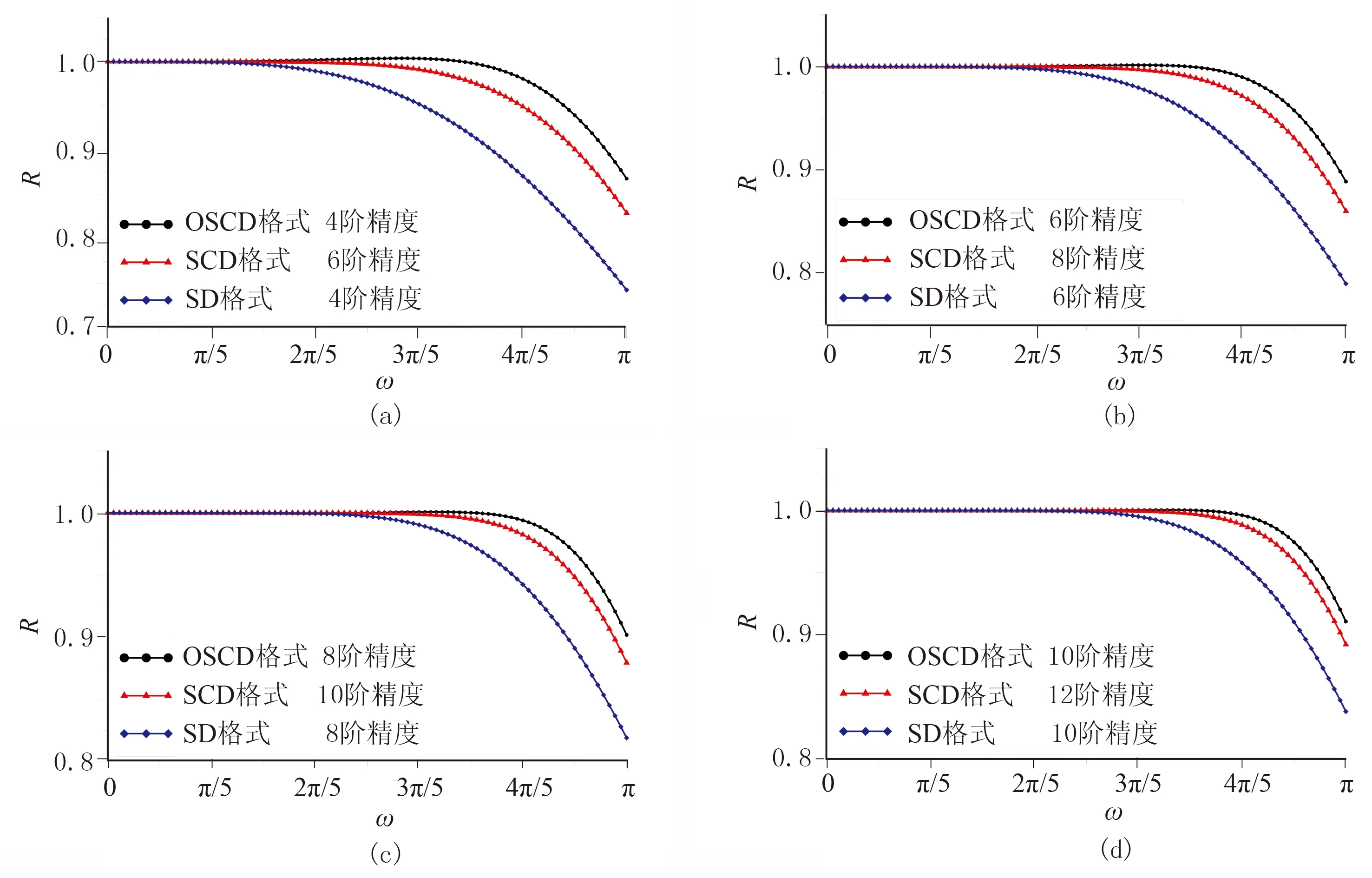
圖1 不同網格節點數三種差分格式的波數比曲線

2.3 精度分析

為了比較SD、SCD和OSCD三種格式的近似精度，對比分析其截斷誤差。從表3可見： 在達到相同空間近似精度的條件下，4和6階精度的OSCD格式具有更小的截斷誤差，8和10階時誤差介于SD和SCD之間，所以低階差分時OSCD格式的精度優勢更明顯。

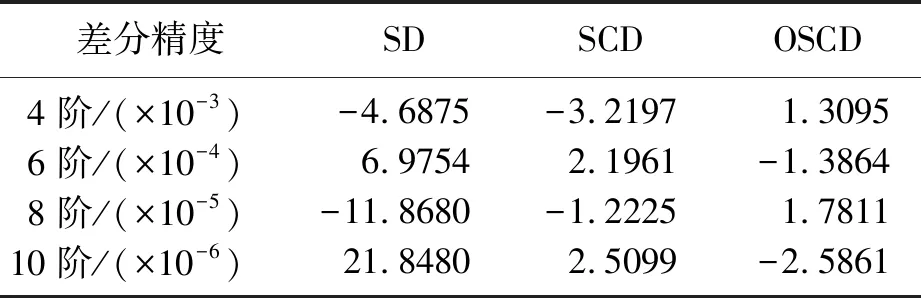
表3 不同差分格式的一階導數截斷誤差主項系數比較

利用一維平面簡諧波初值問題，比較SD、SCD和OSCD格式的數值模擬精度。一維平面諧波初值問題可表示為

(19)

該偏微分方程的達朗貝爾解，即精確的解析解為

(20)

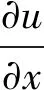
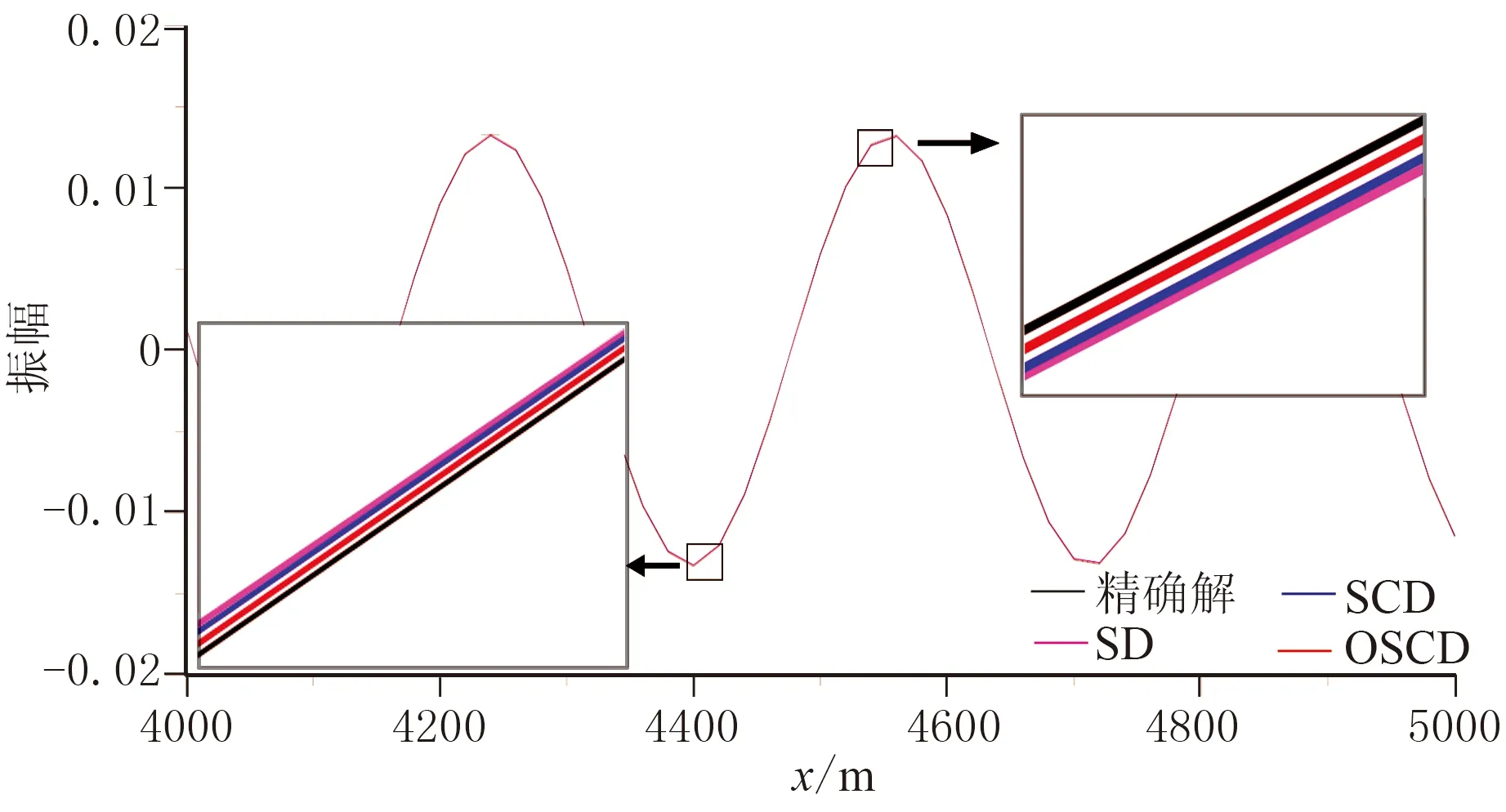
圖2 三種差分格式的一維聲波方程數值模擬快照

通過定量計算，可得到該時刻、4000～5000m之間，OSCD、SCD和SD格式數值解與解析解之間的相對誤差依次為0.33%、0.77%和0.97%，這正是由于它們在計算空間導數時存在不同截斷誤差造成的，這也與表3的理論分析結果相一致。相對誤差定義為

(21)

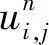
2.4 穩定性分析

按照董良國等[3]和杜啟振等[4]使用的Fourier方法對差分格式進行穩定性分析，略去推導過程，直接給出式(22)表示的二維聲波一階速度—應力方程組(2M，2N)階差分精度的緊致交錯網格差分格式的穩定性條件。

(22)

其中

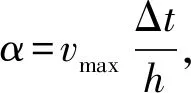
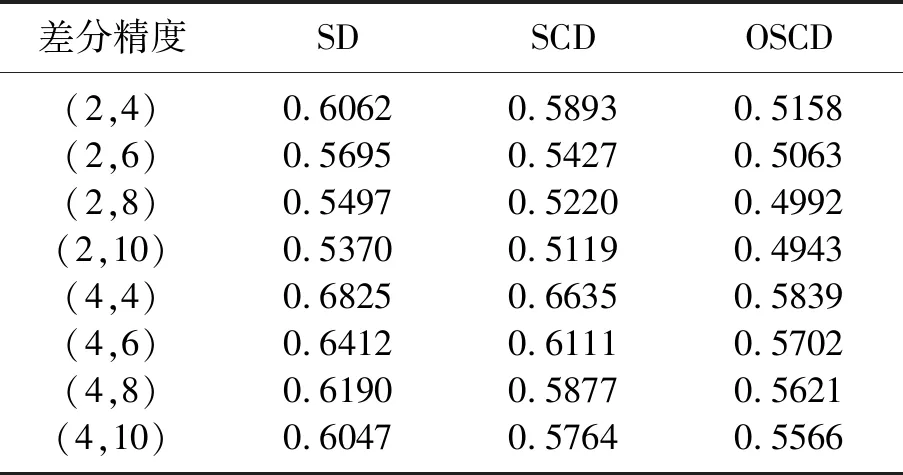
表4 二維聲波方程不同差分格式的Courant數

3 模型試算

采用OSCD差分格式對簡單模型和復雜的Marmousi模型進行二維聲波方程進行數值模擬，檢驗該方法數值模擬的適用性。

3.1 均勻介質模型

為比較SD、SCD和OSCD三種差分方法的差異，設置模型尺寸為3000m×3000m，縱波速度為2000m/s，模型中心加載正弦衰減子波，峰值頻率為30Hz，空間網格為12m×12m，時間步長為1ms。采用三種格式的時間2階、空間4～8階差分精度對一階速度—應力聲波方程進行波場模擬，得到同一時刻的應力P分量的波場快照(圖3)。

在時間和空間網格尺寸相同的情況下，圖3a所示的4～8階SD格式的波場快照頻散非常嚴重；圖3b的4～8階SCD格式波場快照好于SD格式，但4階SCD格式頻散依然明顯，6階在0°和90°方向上也存在較明顯頻散，8階精度時波場快照較清晰，頻散得到較好壓制； 圖3c的4～8階OSCD格式波場快照均很清晰，幾乎看不到數值頻散。與圖1的理論分析結果一致，4階OSCD格式(圖3c左)不僅明顯好于4階SCD格式(圖3b左)，也要好于使用了相同節點數的6階SCD格式(圖3b中)，達到了8階SCD格式(圖3b右)的效果。若要SD和SCD格式達到與OSCD相同的數值模擬效果，在相同網格步長條件下，必須增加差分節點提高差分精度，所以OSCD格式能使用較少的差分節點，從而減少了運算量，提高了計算效率。

3.2 水平層狀介質模型

設置四層水平層狀介質模型，模型長度和深度均為2000m，各層厚度均為500m，縱波速度以500m/s間隔，從3000m/s增至4500m/s，密度由Gardner經驗公式得到。在地表(1000m，0)處激發主頻為20Hz的雷克子波(震源)，時間步長Δt=1ms，記錄時間長度為1s。邊界處理采用分裂的PML邊界條件對邊界反射進行吸收衰減，其控制方程見文獻[7]，此處不贅述。

理論分析和均勻介質模擬都說明了常規SD格式與SCD和OSCD格式相比，不利于壓制數值頻散，所以下文中不再對常規SD格式進行分析，只比較SCD和OSCD的數值模擬結果。在都使用4個網格節點情況下，也就是利用4階OSCD格式和6階SCD格式進行數值模擬，并采用不同的網格尺寸進行計算，數值模擬地表接收的單炮記錄(長度為1s)如圖4所示。所有地震記錄使用同樣的參數進行增益處理，并提取x=1000m處質點模擬得到的不含直達波單道地震記錄(圖5)。

從圖4和圖5可看出，隨著網格尺寸h的增加，數值頻散總體上逐漸變得嚴重。圖4顯示6階SCD格式和4階OSCD格式分別最大在15m和17m時地震記錄清晰，無明顯數值頻散和邊界反射； 圖5中單道記錄在波尾處也無抖動，SCD和OSCD分別從16m和18m開始出現“拖尾”現象。僅以該模型的單個變量而言，15m網格SCD格式的網格數約為133×133，17m網格OSCD格式的網格數為117×117，相對減少內存23%，也減少了運算時間，這對于大尺度模型的數值模擬或逆時偏移還是比較有意義的。

圖3 4階(左)、6階(中)、8階(右)三種格式模擬的600ms時刻波場快照

3.3 Marmousi模型

為了驗證OSCD格式對復雜介質的適用性，用經典二維Marmousi縱波速度模型(圖6)做數值模擬。模型的速度范圍是1729～5500m/s，根據Gardner公式ρ=0.31v0.25，得到密度范圍是2.00～2.67g/cm3。模型范圍是501×501個網格點，空間網格尺寸取12m，時間步長取0.8ms，縱波震源位于地表中心位置，激發30Hz的Ricker子波，采樣時間3s，采用20層PML吸收邊界。

在上節主要對比了4階OSCD與6階SCD格式，本節對比6階OSCD與8階SCD格式數值模擬的結果。一方面驗證OSCD格式對復雜介質的適用性； 另一方面驗證本文方法對其他精度SCD格式的優化效果。圖7是分別使用優化前8階SCD和優化后6階OSCD格式得到的地震記錄，時間精度均為2階。為了顯示清晰，對地震記錄進行了瞬時自動增益控制(AGC)處理，時窗為500ms。

圖4 水平層狀介質的不同網格尺寸時6階SCD (a)和4階OSCD (b)格式模擬地面地震記錄

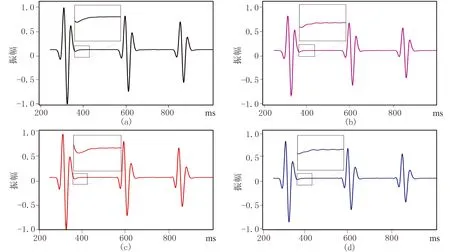
圖5 不同網格尺寸的6階SCD(上)、4階OSCD(下)格式單道地震記錄對比

從圖7中虛線方框所圈定范圍的地震波場看，優化前的8階SCD格式存在較明顯的數值頻散，不利于波場特征分析或偏移成像處理； 而優化差分系數后的6階OSCD格式數值頻散減弱，直達波、反射波及繞射波等波型清晰可見，且邊界吸收效果較好，驗證了本文算法對復雜模型的適用性。

4 結論

基于頻散關系保持的思想，本文利用最小平方法和拉格朗日乘數法對一階導數的緊致交錯差分格式的差分系數進行了優化，對比了優化前、后差分格式的頻散關系和模擬精度，以及一階速度—應力聲波方程組優化前、后緊致交錯差分格式的穩定性條件，獲得以下認識。

(1)相同的差分精度時，與常規SD和SCD格式相比，OSCD格式具有更小的數值頻散、更小的截斷誤差、更高的計算精度。

(2)相同的網格參數時，優化后4階OSCD格式在壓制數值頻散方面優于6階SCD格式，能達到8階SCD格式的效果，即可使用更少的計算節點(算子長度)，提高了計算效率。

(3)相同的計算節點時，優化后的OSCD格式雖然比優化前的SCD格式精度降低2階，但能更好地壓制數值頻散，即OSCD格式能使用更粗的空間網格進行計算，因而節省了內存容量，更適用于粗網格下的大尺度的地震波場數值模擬。

(4)優化差分系數后，聲波方程的穩定性條件比優化前略微嚴格，但總體上差別不大。Courant數隨空間差分精度的增加而減小，隨時間差分精度的增加而增加。高階的時間精度會轉換為更高階的空間導數，勢必會增加內存和運算時間，所以數值模擬中，應兼顧計算精度與效率，選取適宜的差分階數、空間和時間步長。

(5)本文從積分方程表示的修正波數與真波數之間的誤差出發，利用拉格朗日乘數法求取優化差分系數，積分上限是采用多次試驗得到的3π/4。后續研究中，擬從方程最優解角度選定適用于不同差分階數的積分上限，從而得到不同的優化差分系數，并進行對比和分析，找到最佳優化差分系數。