加權平均值在高中物理中的應用
葉銀
摘 要:本文介紹了加權平均值與一般算術平均值的區別,區分對時間的平均值和對位移的平均值,明確常用的平均速度其實是速度對時間的加權平均值,利用平均速度可以快速求解常見的安培力沖量,巧解洛倫茲力沖量.
關鍵詞:加權平均值;平均速度;變力沖量
文章編號:1008-4134(2019)17-0060中圖分類號:G633.7文獻標識碼:B
初中階段學生已經掌握求勻速直線運動的位移、求恒力做功、求恒定電流的電荷量等問題的方法,那么又如何解決變速直線運動的位移、求變力做功、求變力的沖量等問題呢?用微分累積化“變”為“不變”可以很好地解決這類問題,但是在中學階段學生還未系統地學習微積分和微元法,對微分思想的認識還不夠深入,在處理實際問題時,應該盡量回避用微分思想解決問題.平均值是學生已經掌握的概念,求某個變化的物理量的平均值,實際上是找一個恒定的物理量,讓它的效果與該變化的物理量相同,實現“等效替代”.在物理學中涉及的平均值大多是加權平均值,由于學生對加權平均值的概念理解不夠,尤其是不能很好地區分對時間的平均和對位移的平均,在解決實際問題時經常容易混淆.
1 發現問題
例1 如圖1所示,水平放置的光滑平行導軌,固定在桌面上,導軌間距為L,處在豎直向下的磁感應強度為B的勻強磁場當中.桌子離開地面的高度為H.初始時刻,質量為m的M桿與導軌垂直且處于靜止,距離導軌邊緣為d.質量同為m的P桿與軌道垂直,以初速度v0進入磁場區域.最終兩桿先后落在地面上.已知兩桿的電阻均為R,導軌電阻不計,兩桿落地點之間距離為s.求M桿射出時,P桿運動的距離.
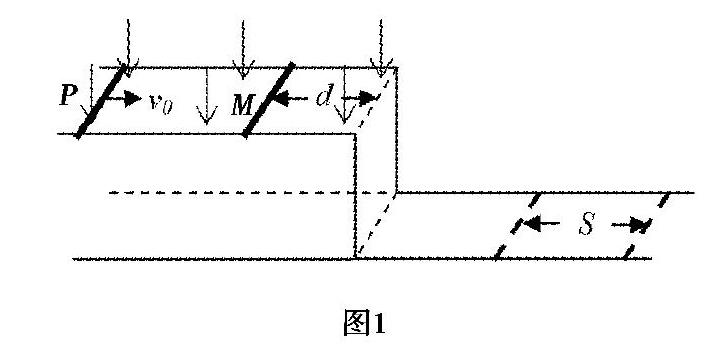
錯誤解法:根據題干條件可知,最終M桿的速度一定小于P桿.

設M桿平拋的水平距離為x,則P桿拋出的水平位移為x+s,根據平拋運動的規律和動量守恒定律有
H=12gt2
x=vMt
x+s=vPt
mv0=mvp+mvM
解得:vp=12(v0+sg2H),vM=12(v0-sg2H)
設M桿射出時,P桿運動的距離為xP,由于P桿和M桿所受的安培力大小始終相等,設安培力的平均值為安,對M桿應用動能定理有
安d=12mv2M
對P桿用動能定理有
-安xp=12mv2P-12mv20
兩式聯立,解得xP=4v20d-dv0+sg2H2v0-sg2H2
粗略一看,先用平拋運動的規律求出P桿和M桿拋出時的速度,再對P、M桿分別用動能定理,思路非常清晰.但經過深入分析,發現這里對安培力的平均值安的定義是模糊的.P桿和M桿所受的安培力時刻都相等,那么安培力的平均值是不是就一定相等呢?要搞清楚這個問題,就要先弄明白什么是平均值.
2 算術平均值和加權平均值
最簡單的平均值是算術平均值,是指一組數中所有數據求和再除以數據的個數.即
= x1+ x2+ x3+…+ xn n
比如有5個學生參加考試,得分分別是82、78、88、64、93,其平均分是
82+78+88+64+935=81


什么是加權平均值呢?舉個例子:某校有5個班級,編號為1班至5班,人數分別是32人、35人、32人、45人和30人.在某次考試中,1班至5班的平均分分別是82分、78分、88分、64分和93分,那么這5個班級的總平均分是82+78+88+64+935=81嗎?顯然不是,因為在用每個班的平均分之和再除以班級總數的時候,每個平均分對應的班級人數是不同的,因此,每個平均分所占的比重應該不同.平均分為64分的4班有45人,人數最多,顯然應該占有更多的比重,平均分為93分的5班有30人,人數最少,顯然應該占有較小的比重.
我們可以這樣來求所有學生的總平均分:
=32×82+35×78+32×88+45×64+30×9332+35+32+45+30
=79.54
物理量x的加權平均值一般表達式可以寫成
= w1 x1+ w2 x2+ w3 x3+ … + wn xn w1+ w2+ w3+ … + wn= ∑n1wi xi ∑n1wi
其中wi∑n1wi 代表xi所占的權重比.
3 直線運動中速度對時間的加權平均值
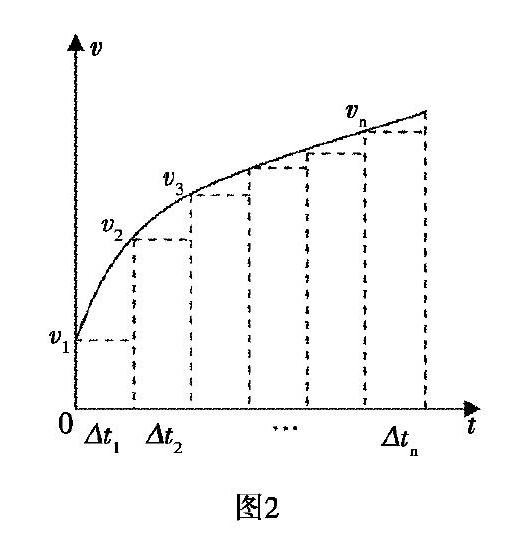
在求變速直線運動的位移時,高中階段常利用v-t圖象包圍的面積來處理.在處理時,先將整個過程分割成無數個子過程,每個子過程的時間分別是Δt1、Δt2、…Δtnn→∞.由于每個子過程的時間很短,可以用每個子過程的初速度vi來近似描述該子過程運動的快慢,整個過程速度對時間的加權平均值為
v-=v1Δt1+v2Δt2+…+vnΔtnΔt1+Δt2+…+Δtn
其中v1Δt1+v2Δt2+…+vnΔtn等于總位移 x,Δt1+Δt2+…+Δtn等于總時間t.根據平均速度的定義v-=xt可知,速度對時間的加權平均值其實就是平均速度,而由x=v-t可知,我們可以用速度對時間的加權平均值(以下簡稱平均速度)乘以時間來求總位移,如圖2所示.由于動生電動勢E=BLvsinθ和洛倫茲力f洛=qvBsinθ中都涉及速度v這個物理量,所以在其他物理量不變的情況下,動生電動勢、洛倫茲力對時間的加權平均值可以利用平均速度乘以時間來求.
4 區分對時間的加權平均值和對位移的加權平均值
由加權平均值的概念可知,用力對位移的加權平均值乘以位移可以求功,W=Fxx,用力對時間的加權平均值乘以時間可以求沖量,I=tt.但是在求解具體問題時,兩者容易混淆.
例2 質量為m=50kg的鐵錘從離木樁h=1.8m高處靜止下落,打到質量M=150kg的木樁上,鐵錘碰后不彈起,結果木樁被打入土中d=20cm深,求此過程中木樁受到土地的平均作用力.(不計空氣阻力,g取10m/s2)
解:從鐵錘開始下落到剛接觸木樁由動能定理有
mgh=12mv2
v=6m/s
鐵錘和木樁碰撞后不分開,根據動量守恒定律有
mv=m+Mv1
v1=1.5m/s
碰撞后到木樁靜止,由動能定理有

m+Mgd-Fd=0-12m+Mv21
解得:F=1325N.
例3 一鐵球,從靜止狀態由h=5m高處自由下落,然后陷入泥潭中,從進入泥潭到靜止用時t=0.5s,該鐵球的質量m=0.5kg,求泥潭對小球的平均作用力.(不計空氣阻力,g取10m/s2)
解:從鐵球開始下落到剛接觸地面由動能定理有
mgh=12mv2
v=10m/s
從接觸地面到靜止,根據動量定理有
mgt-Ft=0-mv
得F=15N.
例2和例3中看起來都是求平均作用力,但是例2中運用了動能定理,其中涉及的功是力的空間累積效應,所以以此求得的平均作用力是對位移的加權平均值;而例3中運用的是動量定理,其中涉及的沖量是力的時間累積效應,以此求得的平均作用力是對時間的加權平均值.如果不能很好地區分到底是對哪個變量的加權平均值,很容易張冠李戴.
我們再來分析例1:在求得P桿和M桿水平射出的速度后,對兩桿用動能定理時,式中的安應該用安培力對于位移的加權平均值.根據題意,任意時刻兩桿所受安培力大小始終相等,因此兩桿中的安培力對時間的加權平均值是一樣的,但是兩桿在任意相同時間內的位移不同,導致兩桿的安培力對位移的加權平均值是不一樣的,因此無法通過兩式消去安.
正確的解法:求得P桿和M桿拋出時的速度后,假設從開始到M桿射出時,P桿運動的距離為x,對P桿用動量定理有
-安t=mvP-mv0
其中,安為安培力對時間的加權平均值,由于B、L、R為常數,所以
安=BL
=2R
=BLv-P-v-M
代入動量定理方程可得
-BBLv-P-v-M2RLt=mvP-mv0
此處v-P和v-M應是P桿和M桿速度對時間的加權平均值,則
v-Pt=x

v-Mt=d

代入可得x=d+RmB2L2v0-sg2H
5 利用平均速度求安培力沖量
在有電磁感應的動力學問題中經常需要求安培力的沖量,當安培力是變力的時候,可以用安培力對時間的加權平均值來求安培力沖量.當其他物理量不變的情況下,可以利用平均速度快速地求出安培力沖量.
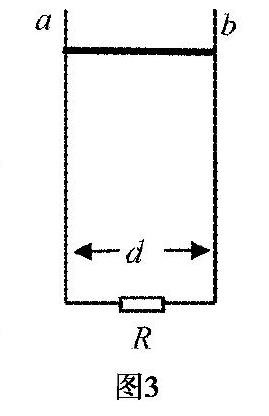
例4 如圖3所示,兩根相互平行、間距為d的豎直導軌,下端連接阻值為R的電阻.在豎直導軌間的區域僅有垂直紙面的勻強磁場B(未畫出).一根阻值為R1、質量為m的導體棒ab從靜止開始下滑,經t時間后下降了h,求此過程產生的焦耳熱.假設棒始終與導軌垂直,且與導軌接觸良好,不計摩擦阻力和導軌電阻.
解 取豎直向下為正方向,該過程對導體棒用動量定理有

