巧用埃拉托色尼篩選法統計大數據區間內素數算法剖析

周靜

摘要：本文從常規算法出發找尋并統計素數，探討了常規算法在大數據區間找尋并統計素數的低效問題，引出巧妙運用埃拉托色尼篩選法統計大數據區間范圍內素數個數方法，并詳細剖析該方法算法思路。

關鍵詞：素數;埃拉托色尼篩選法;大數據區間;統計

找尋素數的題目屢見不鮮，總會出現在一些編程教材中。找尋方法都是沿用對素數判斷規則，即逐一判斷找尋范圍內的數，在2至其平方根范圍內是否存在因子，如果存在就不是素數，如果不存在就是素數。這種判斷方法是沿用素數的定義，也讓初學者能輕松理解并掌握控制流程的好方法。但是當區間范圍過大以及找尋的數據本身也足夠大時，統計速度慢的弊端就會顯現出來，完全體現不了現今信息時代所提倡的高效性，怎么來解決對大數據區間素數統計問題呢？

1 常規統計素數方法的低效問題

對于素數統計，總會想到先判斷是不是素數，再執行統計。這是思考問題的常規思路。但是判斷一個數是不是素數，所采用常規判斷素數方法使用“窮舉法”排除非素數，窮舉出從2至其平方根中是否存在因子，只要存在則排除。當需要判斷的數據過大，使用 “窮舉法”就會變得很低效。

窮舉算法低效在于需要判斷的數據可能會在十億至四十多億，需要在2至其平方根（即好幾萬）進行逐一的因子判斷，其耗時比預想要大得多，且是在一個大區間內統計，需要進行素數判斷的大數據數量眾多，造成了統計耗時的成倍增長，運行低效問題也更突出。怎樣才能高效實現在大數據區間內的素數統計呢？

2 巧妙統計素數方法的高效原理

在編程語言（C++）中，正整數最大范圍可以達到42億多，如果判斷這個數據是否是素數，使用以上常規判斷不可取的。如果能有一個空間來描述某個范圍內哪些是素數，就可以通過檢索這個空間來統計素數的數量。

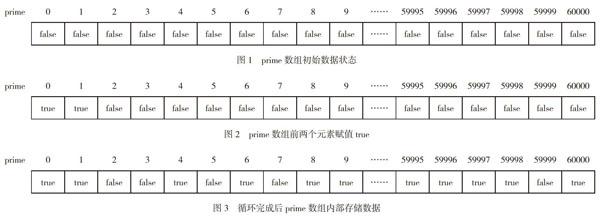
一個區間范圍內統計素數只有兩種可能，是或不是，使用C++中的布爾值false和true來表示。定義布爾型數組：bool prime[60001];用該數組來描述0-60000范圍內哪些是素數，數組元素的默認值為false，即假設其都是素數，prime數組初始化如圖1所示：

在0-60000數字中，對于其中的0和1，已知其不是素數，所以為數組元素prime[0]和prime[1]賦值true，表示其不是素數，如圖2所示。

從數字2開始判斷其是素數，但后面所有是2倍數的數就都不是素數，為其賦值true，這就是埃拉托色尼篩選法的中心思想，算法實現：

for（long i=2;i<=60000;i++）

if（！prime[i]） {

for（long j=i+i;j<=60000;j=j+i）

prime[j]=true;

}

通過以上代碼的執行，在prime數組中就記錄0至60000哪些是素數（值為false就是素數）的信息。prime數組的表示如圖3所示：

這種方法可以將60000內所有非素數置true，是因為只要不是素數就會存在因子，其因子如果也不是素數，可以繼續分解，總之一個非素數都可以表達成比它小的素數乘積，即是素數倍數，既然是素數倍數，根據前面的說法，就應該為其賦值為true，標識出其不是素數了。

其高效體現在代碼中進入內循環存在條件，且內循環次數隨i值的遞增，將成i倍遞減，與逐一判斷是否存在因子的素數判斷作為內循環的效率是不可相提并論的。

對大數據區間素數統計該怎么實現呢？在實現代碼中使用了prime數組存儲布爾值來描述0-60000中哪些是素數。定義數組大小為60000的原因是因為描述素數范圍最大數是42億多，取其平方根是60000多，當得到60000以內的所有素數，再以這些素數為基礎，將需要描述的大數據范圍內素數倍數都賦值為true，素數統計工作就只需要單層循環檢索即可實現。

注意需要了解找尋的大數據范圍數量，才能設計一個空間來描述這些數中哪些是素數。可以預想一下需要判斷的區間范圍，假如是1，000，000，那么需要設計1，000，000的空間來描述該范圍內數據是否是素數。即：bool primeMax[1000001];該數組就用來描述這個大數據范圍內的數哪些是素數。

描述的數據范圍有3種情況：

第一種是當描述數據都在60000以內;

第二種需要描述的數據一部分在60000以內，一部分在60000以外;

第三種是需要描述的數據都在60000以外;

這里用整型變量left表示范圍左邊界值，用整型變量right表示右邊界值，用整型變量count且初始化值為0來累加統計素數量。

（1）第一種情況的統計處理

if（right<=60000）{

for（long i=left;i<=right;i++）

if（！prime[i]）count++;

cout<

}

直接利用prime數組統計完需要描述的區間范圍內的素數個數并輸出;

（2）第二種情況的統計處理

需要分段處理，首先處理在60000以內的數據，這些數據按第一種情況處理;其次處理不在60000以內的數據，這些數據可以按第三種情況處理。

① 第一段數據（在60000以內的數據）統計處理。

if（left<=60000）{

for（long i=left;i<=60000;i++）

if（！prime[i]）count++;

left=60001;

}

② 第二段數據（在60000以外的數據）統計處理

上面第一段數據統計處理代碼實現最后一條語句將60001賦值給left，作用是改變左邊界值。這樣使得第二段數據可以按下面第三種情況統計處理。

（3）第三種情況的統計處理

需要使用上面定義的primeMax數組來標識60000以外數據是否是素數，該數組如圖4所示：

與prime數組類似，先假設所描述60000以外數據它們全部都是素數，再通過檢索prime數組中的素數，標識需要描述的60000以外的區間內哪些是素數，為其賦值為true。

其代碼實現如下：

long temp;

for（long i=2;i<=60000;i++）{

if（！prime[i]）{

for（unsigned long j=left/i;j<=right/i;j++） {

temp=j*i-left;

if（temp>=0）primeMax[temp]=true;

}

}

}

對于代碼中的left/i和right/i作用是使得內循環次數成i倍遞減表示方法。因為要為素數的倍數置true，表示其不是素數。

prime中描述了所有60000以內的素數，將在給出的大數據范圍內標識出是prime數組中素數倍數的數，將這個表示存儲在primeMax數組中。例如，描述60001-70001范圍;當i=2時;primeMax數組的表示如圖5所示：

代碼中需要置true的primeMax數組元素下標temp=j*i-left;該表達式j*i代表需要描述的大數據，該數據是i的倍數。減去left將該數對應到primeMax數組中相應的元素上;

在為primeMax數組元素賦值true時，有一個if條件語句，需要判斷temp是否大于等于0，該判斷的作用是看描述的大數據j*i，是否在需要描述數據區間范圍內;如果temp小于零，代表j*i小于left左邊界，即不用描述該數據。當標識完prime數組中所有素數在大數據區間內的倍數標識，即為primeMax數組賦值后，就可以實現區間類素數統計了;前面已經實現了用檢索prime數組對60000以內素數統計，現在就對primeMax數組進行檢索，統計60000以外的素數量，其實現代碼是：

for（long i=0;i<=right-left;i++）

if（！primeMax[i]）count++;

cout<

前面詳細講解利用埃拉托色尼篩選法巧妙統計大數據區間內素數，希望大家能理解和掌握該方法，并能靈活借鑒該方法解決其他類似的問題。

基金項目：本文系2018-2019年度工業和信息化職業教育教學科研課題 “藍橋杯”技能大賽成果資源在高職教育教學中的實踐與應用（編號GS-2019-10-02）; 重慶電子工程職業學院卓越技術技能人才工匠工坊項目“千貝軟件工匠工坊”（編號：0319010225 ）的研究成果。

（作者單位：重慶電子工程職業學院）