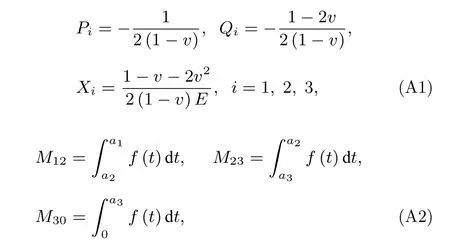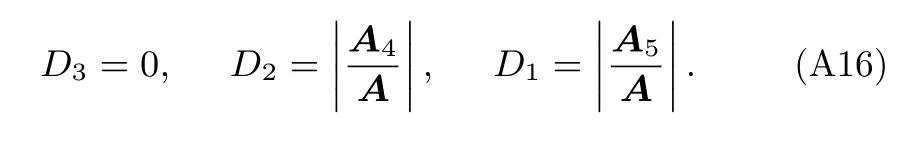臨界電流密度對圓柱狀超導體力學特性的影響*
程鵬 楊育梅
(蘭州理工大學理學院,蘭州 730050)
1 引 言
高溫超導材料不僅具有獨特的零電阻特性、抗磁性及邁斯納效應,同時相較低溫超導材料而言,具有更高的臨界轉變溫度和臨界電流密度,因而備受關注,被廣泛應用于磁懸浮、核聚變磁約束、電機及儲能等裝置中[1?5].然而,超導材料具有明顯的脆性特征,在外加磁場激勵下,結構內產生磁通釘扎力,該釘扎力在外加下降場中產生的拉應力極易引起超導結構的斷裂破壞[6?8].因此,在超導材料的應用中,對其結構內部力學特性的研究就顯得尤為關鍵.Ikuta等[9]通過測試Bi2Sr2CaCu2O超導體在外部磁場作用下出現的力學變形,指明磁通釘扎引起的磁致伸縮對這一變形起主導作用[10].之后Johansen[11,12]分別對長圓柱和長矩形超導體內的應力分布進行了計算,討論了零場冷和場冷兩種情形的應力分布,并給出了應力、應變及位移的解析表達關系式.隨后又研究了薄超導圓盤內的應力分布情況,給出了受退磁效應影響的應力大小和分布曲線[13].Xue等[14]研究了薄超導帶在垂直磁場中的磁彈性行為,分別采用Bean模型和Kim模型計算了超導體內的體力、應變和位移.Huang等[15]運用有限元方法研究了有限厚度的II型超導圓柱體和超導圓環結構內的磁致伸縮行為.上述超導結構力學特性的研究,均基于臨界電流密度均勻分布的假定展開.
然而,超導體內的臨界電流密度具有明顯的非均勻特性[16].Grasso等[17]研究發現,超導體內臨界電流密度從中心到表面逐漸增加.其后,Lehtonen等[18]研究了超導材料中臨界電流密度軸向(沿超導體的軸向變化)和橫向(沿超導體的橫向變化)兩種非均勻分布形式對交流損耗的影響.Inada等[19]研究了臨界電流密度非均勻分布的薄超導帶上的交流損耗特性,并討論了臨界電流密度沿帶寬度方向不均勻性對電纜導體中交流損耗的影響.值得注意的是,目前還沒有考慮到非均勻分布的臨界電流密度對超導結構力學性能的影響.為了更好地解決超導體結構設計和應用中出現的強度和剛度問題,有必要研究臨界電流密度非均勻分布對超導結構力學特性的影響.
本文基于求解平面應變問題的方法[11]和Bean臨界態模型,考慮臨界電流密度沿超導圓柱體半徑方向呈非均勻分布狀態,推導了承載電流上升和下降過程中超導結構內部的磁通密度和電流分布,并給出了結構內徑向應力、環向應力和磁致伸縮的解析表達式,詳細討論了臨界電流密度非均勻分布對超導圓柱體力學性能的影響.
2 模型建立及理論推導
考慮一半徑為R的無限長超導圓柱體,承載沿z方向的電流Ia,如圖1(a)所示.由于臨界電流密度橫向非均勻分布對材料性能的影響更加顯著[18],假定超導體內臨界電流密度在z和q方向的大小和分布是均勻的,沿半徑方向非均勻分布.如圖1(b)所示,將垂直于z軸圓柱狀超導體橫截面延半徑方向分為n層,每層臨界電流密度不同.從外到內臨界電流密度分別為J1,J2,J3,··,Ji,··,Jn–1,Jn,半徑分別為a1,a2,a3,··ai,··,an–1,an.
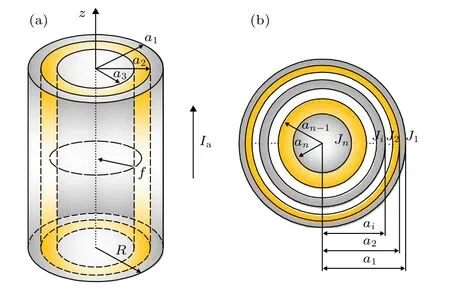
圖1 (a)長圓柱狀超導結構示意圖; (b)臨界電流密度分布示意圖Fig.1.(a) Schematic diagram of a long cylindrical superconducting structure; (b) schematic diagram of critical current density distribution.
鑒于超導塊體中臨界電流密度在中心部分變化較小,而邊緣部分變化比較劇烈[16],為了更好地模擬超導體內臨界電流密度非均勻分布情況,假定每層的橫截面面積為 πR2/n.當n=1 時表示超導結構內臨界電流密度均勻分布,當n>1 時表示結構內的臨界電流密度非均勻分布.在研究超導體特性時發現,2至n?1 層之間的相互影響較為近似,當n>3 時,會使得最外層和最內層非均勻分布的臨界電流密度引起的力學性質變化的區分度降低.且三層模型已具有較高的準確性,應用廣泛[20?22],下面選取n=3 時的情況進行分析.
此時在超導體圓柱體模型中,從外到內分為三層,半徑依次為a1,a2,a3,各層半徑有如下關系:
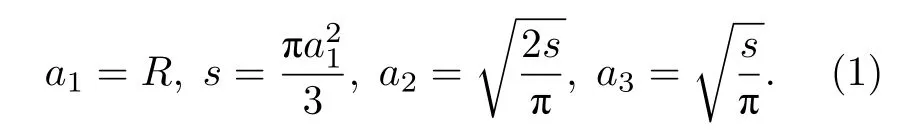
假定第i層內的臨界電流密度為Ji,則第i層內的電流大小為Ii=sJi,圓柱體內前i層的總電流大小為

2.1 超導體內的電流及磁場分布
2.1.1 承載電流增加的情形
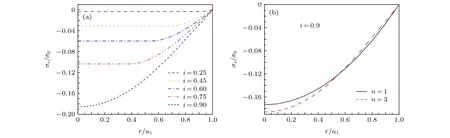
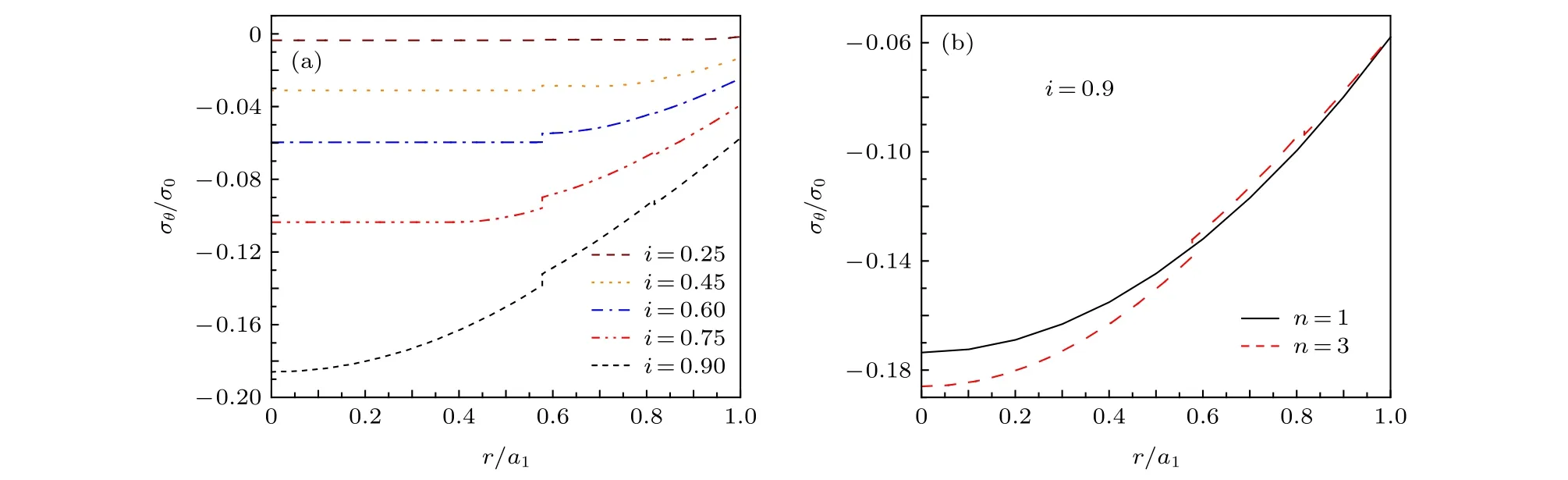
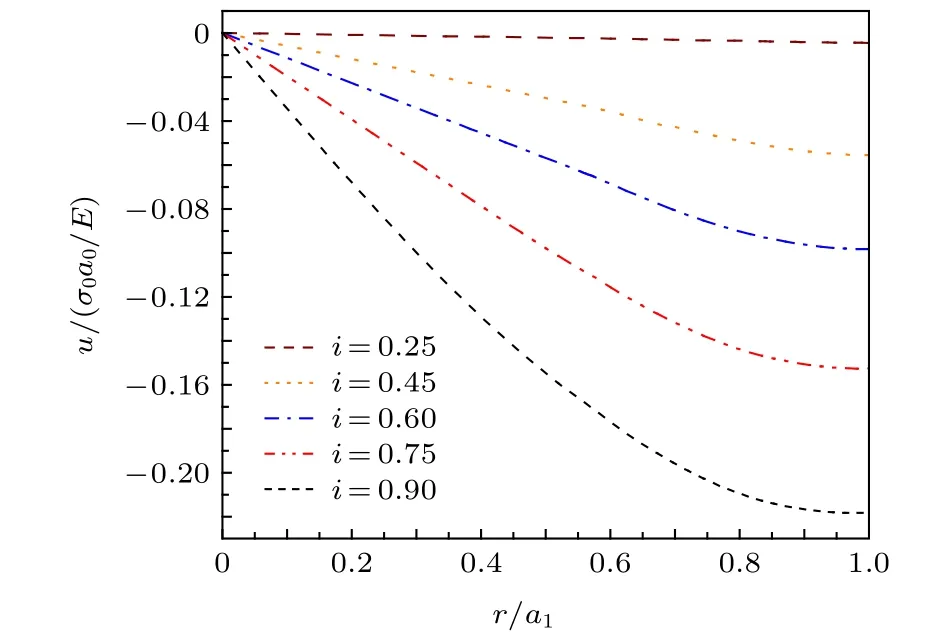
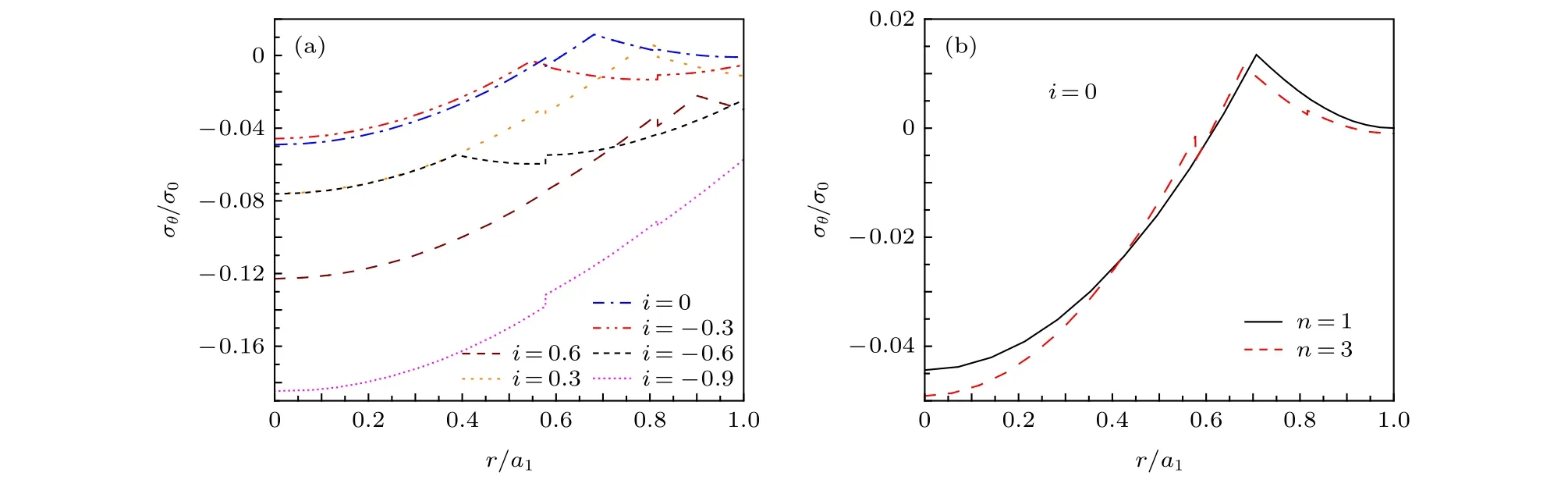
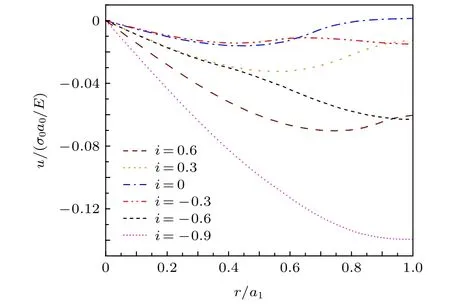
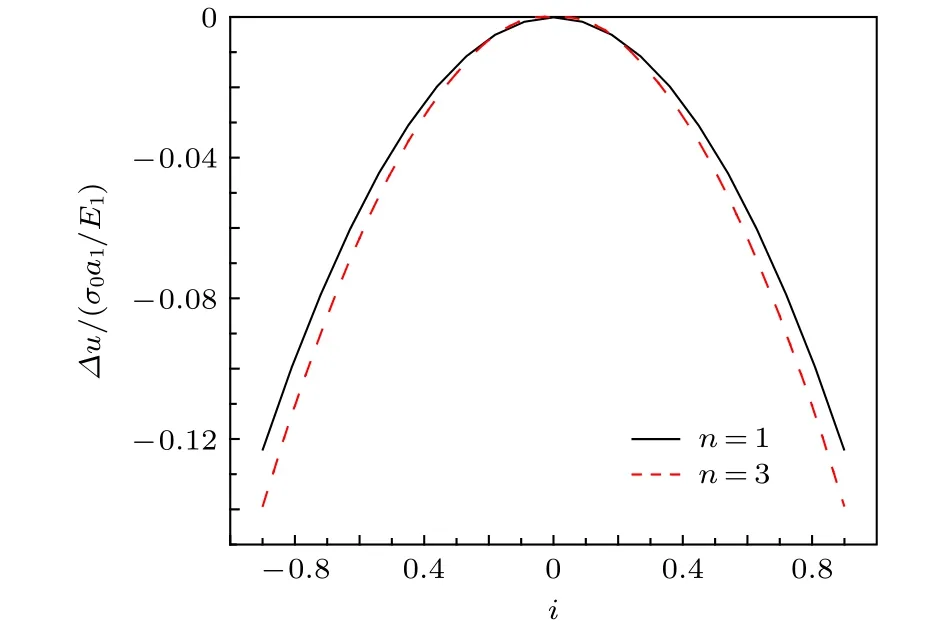
當電流Ia從零開始逐漸增大時,基于臨界態Bean模型,超導結構內各層臨界電流密度J1,J2,J3為常數.根據麥克斯韋方程可得到電流和磁場分布的表達式.當 0 當Ic1 當Ic2 2.1.2 承載電流減小的情形 當超導圓柱體中的承載電流從最大值Ic3開始下降時,超導體內的磁通開始從結構外邊緣排出,此時,結構內的電流及磁通密度按如下方式重新分布,用x0表示超導體內電流發生反向的位置,則有: 當a2 當a3 當 0 由于超導體俘獲磁通線的特性,進入超導體內的磁通線被釘扎在結構內部的缺陷處,該釘扎力的大小等于洛倫茲力的大小: 根據彈性力學平衡方程則得到: 由于超導圓柱體是軸對稱結構,所以結構內部的應力僅與半徑r有關,變形只需要用徑向位移u(r) 來描述,則幾何方程表達為 結合物理方程,應力σr,σθ,σz與應變er,eq,ez之間的關系為[11] 其中E為超導體的楊氏模量,n為泊松比.將(17)和(18)式代入方程(16)可得 求解方程(19)得 防火墻是在內部網與外部網之間構造的保護屏障,能夠防止內部網絡受非法用戶的入侵,防火墻不能夠防范網絡內部的攻擊以及病毒的侵犯。隨著技術的發展,高科技、高智商網絡攻擊已經常態化,黑客也掌握了一些破解方法對防火墻的使用造成一定的安全隱患。 對于本文所研究的問題,需要注意的是在相鄰兩層之間相鄰部分的徑向應力σr和徑向位移u(r)是相等的,則邊界條件可表示為 結合(16)—(20)式,通過平面應變方法[11],可得到圓柱超導體內的徑向應力分布如下: 環向應力的表達式為 徑向位移的表達式為 此時,圓柱體內的磁致伸縮大小為 其中關于P,Q,X,M,N,C1,C2,C3,D1,D2,D3詳細見附錄A. 根據以上理論推導,得到了超導圓柱體內徑向應力、環向應力、徑向位移和磁致伸縮的解析表達式.為便于結果討論,對以下參數歸一化: 圖2和圖3分別為承載電流大小從i=0 增大到i=0.9 時,超導結構內的徑向和環向應力沿半徑方向的分布圖.n=1 時,結構內臨界電流密度β1=0.9;n=3 時,各層的臨界電流密度為β3=1,β2=0.9,β1=0.8.圖2(a)和圖3(a)顯示了n=3 ,i取0.25,0.45,0.6,0.75,0.9時結構內的徑向和環向應力分布情況.可以看出,在整個變化過程中徑向應力都是負的,即為壓應力,其大小沿著半徑指向中心方向逐漸增大并趨于穩定,這是因為在感應磁場未穿透的區域結構內部的體力為零,該區域應力分布的均勻性得到保持.對于較小的承載電流,應力增加相對比較緩慢,而且這兩種應力分別以不同的方式沿指向表面方向減小.徑向應力在表面處減小到零,而環向應力減小到一個不為零的有限值.這些特點與Johansen[11]的研究結果一致.說明臨界電流密度的非均勻分布對超導體內應力整體的變化趨勢影響不顯著.但是由于相鄰部位之間的臨界電流密度的差異而導致結構內的釘扎力分布是不連續的,所以環向應力出現了不連續的現象.在Zheng等[23]關于圓柱形復合超導材料的研究中觀察到類似的現象,但是本研究排除了彈性模量的差異對結果的影響,證明了臨界電流密度的非均勻分布會導致這樣的結果出現. 圖2 上升場情形下結構內的徑向應力的分布 (a) n=3,i取不同值; (b) i=0.9,n取不同值Fig.2.Distribution of radial stress in the structure under the ascending field: (a) n=3,i takes different values; (b) i=0.9,n takes different values. 圖3 上升場情形下結構內的環向應力的分布 (a) n=3,i取不同值; (b) i=0.9,n取不同值Fig.3.Distribution of hoop stress in the structure under the ascending field: (a) n=3,i takes different values; (b) i=0.9,n takes different values. 圖4給出了徑向位移沿半徑方向的分布特性,在整個過程中超導結構的徑向位移都是負的,結構整體是壓縮變形,這與臨界電流密度均勻分布時的變化規律一致. 圖4 上升場情形下結構內的徑向位移沿半徑方向的分布Fig.4.Distribution of radial displacement within the structure along the radial direction in the case of an ascending field. 當超導結構內的承載電流從最大值Ic3開始降低,在圓柱體外部的臨界電流方向開始反向.在這個再磁化區域中,體力方向沿著對稱軸心向外,然而內部的體力方向仍然保持不變.接下來將仔細研究下降場時超導結構應力的變化情況. 圖5和圖6分別為承載電流從最大值i=0.9開始減小時,超導結構內的徑向和環向應力沿半徑方向的分布特性.其中,臨界電流密度采用與圖2和圖3相同的計算參數.圖5(a)和圖6(a)顯示了n=3,i分別取0.6,0.3,0,–0.3,–0.6,–0.9時結構內的徑向和環向應力分布情況.可以看出,承載電流下降階段,應力的大小沿著半徑指向中心方向先上升后降低.而產生的極值在數值上先增大后減小并在i=0 附近取得最大值.這是由于在下降場階段,超導結構內的臨界電流從最外部開始反向,這導致了結構內部拉應力和壓應力同時存在.這種情況下超導體發生破壞的風險最高,而環向上不僅拉應力和壓應力同時存在而且在臨界電流密度有差異處呈不連續的分布,這就要求將此類超導材料應用于對抗剪強度有要求的結構時需要慎重. 圖5 下降場中結構內的徑向應力沿半徑方向的分布 (a) n=3,i取不同值; (b) i=0,n取不同值Fig.5.Distribution of radial stress in the structure in the falling field along the radial direction: (a) n=3,i takes different values;(b) i=0,n takes different values. 圖6 下降場中結構內的環向應力沿半徑方向的分布 (a) n=3,i取不同值; (b) i=0,n取不同值Fig.6.Distribution of the hoop stress in the structure in the falling field along the radial direction: (a) n=3,i takes different values; (b) i=0,n takes different values. 圖5(b)和圖6(b)分別顯示了i=0 ,n=1,3時,超導結構內的徑向和環向應力沿半徑方向的分布情況.可以看出,由于n=3 時臨界電流密度分布不均勻,導致超導體中心部分n=3 時的應力較n=1時更大,而靠近表面處n=1 時的應力較大.從圖5(b)可以看到臨界電流密度的非均勻分布導致拉應力的峰值明顯大于均勻分布時的數值.而這一拉應力極易引起超導體發生斷裂或者己有裂紋的擴展.這說明臨界電流密度的非均勻分布可能會導致超導體更容易發生破壞.圖7給出了超導結構沿半徑方向的徑向位移分布特性.從徑向位移的變化趨勢可以看出,下降場情形中徑向位移的變化規律變得復雜,結構內部會出現了拉應變和壓應變共同存在的情況.比如i=?0.3 時,甚至出現超導結構中心和邊緣處產生壓應變而中間處產生拉應變.這是下降階段超導結構內徑向拉應力和壓應力同時存在并且臨界電流密度非均勻分布共同作用的結果. 圖7 下降場中結構內的徑向位移沿半徑方向的分布Fig.7.Distribution of radial displacement within the structure in the descending field along the radial direction. 圖8展示了承載電流i從0.9降低到–0.9過程中,n=1和n=3 時的磁致伸縮分布圖.和預期一致[23],均勻材料的磁致伸縮不存在磁滯回線.但觀察臨界電流密度非均勻分布時可以發現,產生的磁致伸縮在整個變化過程中都大于均勻分布的情況.并且在承載電流取最大值時差值最大,即臨界電流密度的非均勻分布導致超導結構產生更大的變形.因此為了提升超導材料應用的可靠性,需要密切關注臨界電流密度的分布性質. 圖8 臨界電流密度分布不同時超導圓柱體的磁致伸縮Fig.8.Magnetostriction of a superconducting cylinder with different critical current density distributions. 本文考慮超導體內臨界電流密度的非均勻分布,基于Bean臨界態模型和平面應變方法,研究了臨界電流密度在結構內非均勻分布時的應力、位移和磁致伸縮特性.與均勻分布情況對比可以得到,上升場時,臨界電流密度的分布不影響超導結構內應力和位移的變化趨勢,但局部應力的數值會隨著臨界電流密度的非均勻分布而發生變化,在局部臨界電流密度較大處壓應力數值較大.且臨界電流密度的非均勻分布導致超導體內應力出現更大的極值,因此發生破壞的風險較均勻分布情況下更高,對強度有著更高的要求.而在下降場時,臨界電流密度明顯影響拉應力和磁致伸縮特性,使得非均勻分布時拉應力峰值和磁致伸縮數值大于均勻分布時的數值,而環向應力不僅拉應力和壓應力同時存在而且在臨界電流密度不連續處顯示出了不連續的特點.這就導致對超導結構抗剪強度有著更高的要求.而磁致伸縮的程度也比均勻分布情況下更高,即臨界電流密度的非均勻分布導致超導結構產生更大的變形,所以相應的剛度要求也會發生變化.因此,在高溫超導體實際應用中,必須要充分考慮臨界電流密度非均勻分布導致的超導材料結構強度降低,以保證其在工程應用中的安全性. 附錄A 參量表達式 (22)—(25)式中P,Q,X,M,N,C1,C2,C3,D1,D2,D3的表達式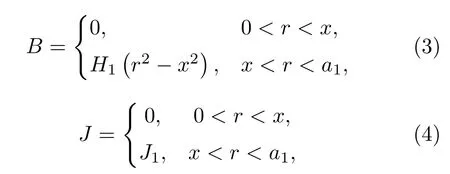
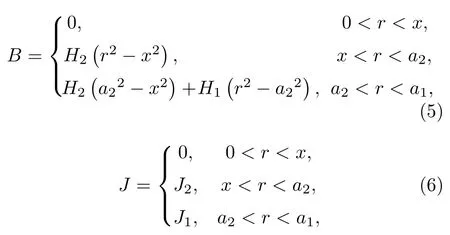


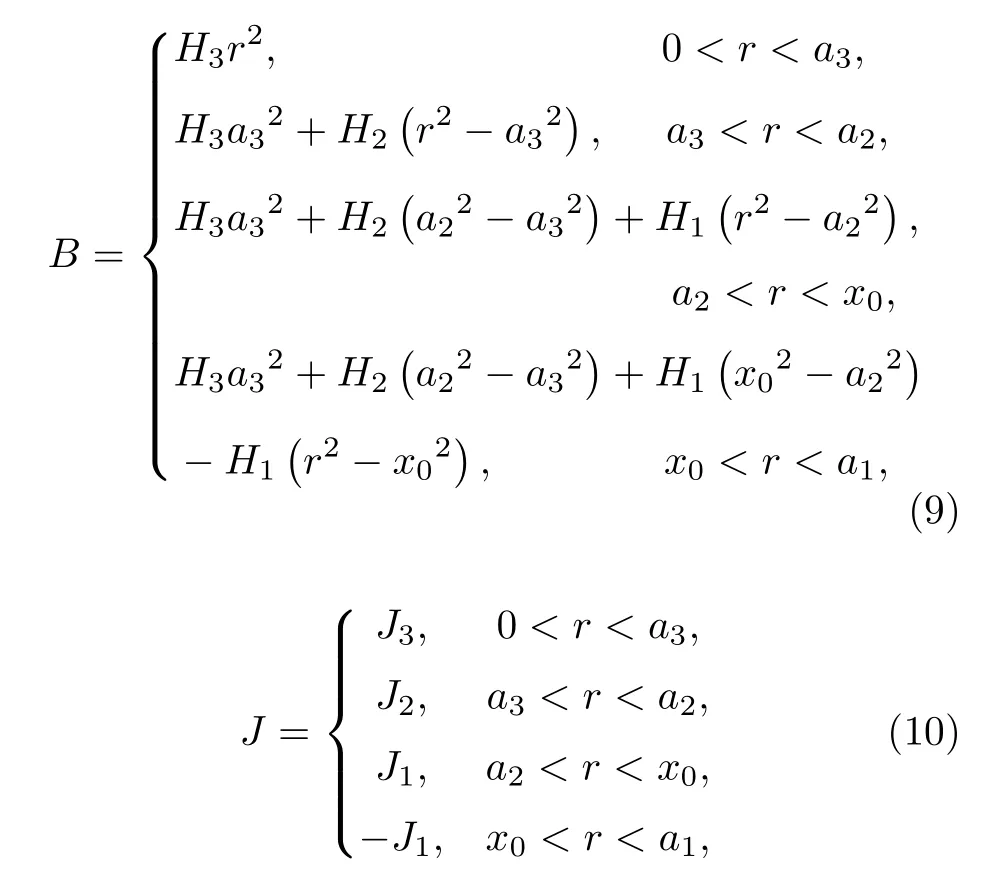
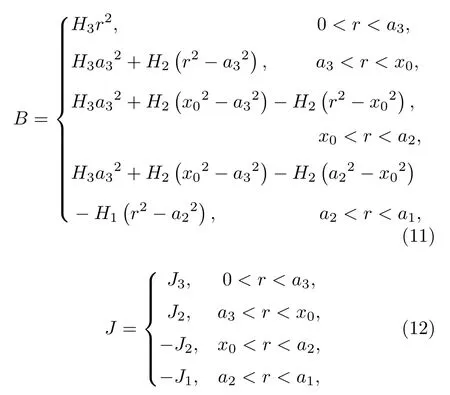
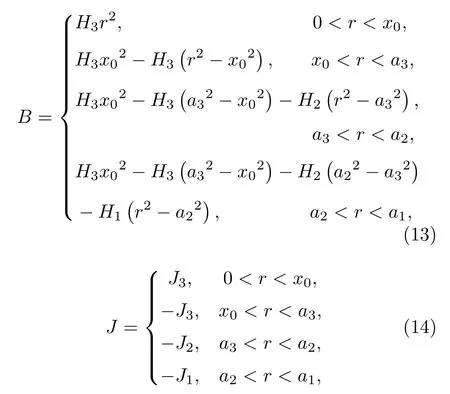
2.2 超導體內的力學響應計算



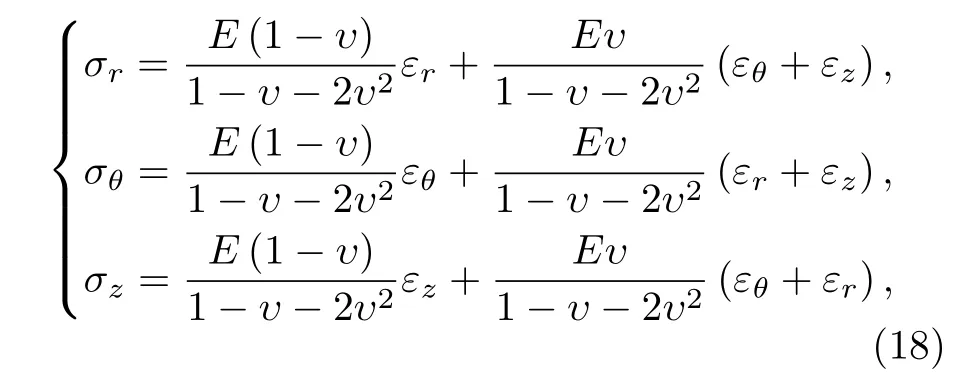
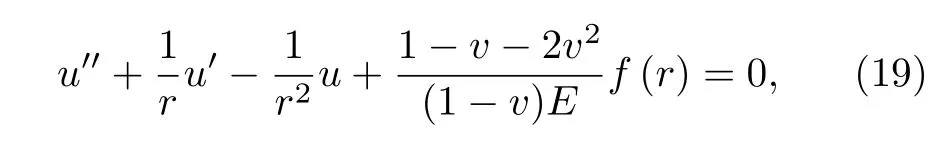
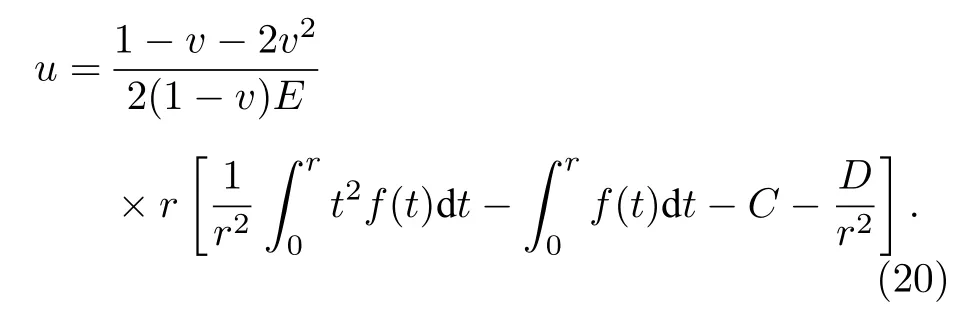
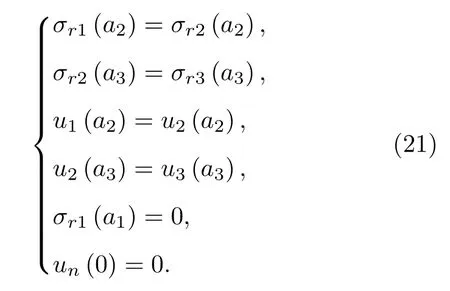

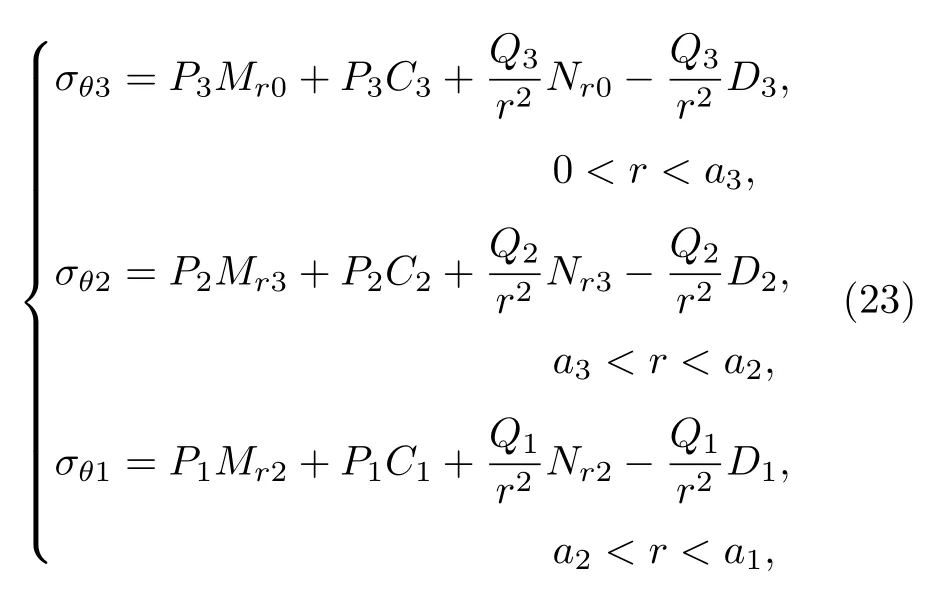

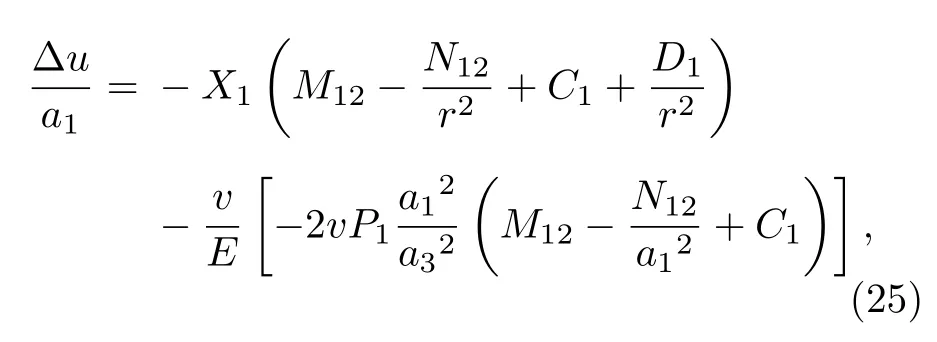
3 結果與討論
3.1 上升場情形

3.2 下降場情形
3.3 磁致伸縮
4 結 論