基于圖像增強技術的SURF 特征匹配算法研究
張明浩,楊耀權,靳渤文
(華北電力大學 控制與計算機學院,保定071003)
圖像匹配技術是圖像處理中的一項重要技術。其目的是對2 個或者多個圖像的特征紋理、內容等因素進行分析并匹配。 對點特征的匹配是圖像匹配中的一個基本方法。 其中,SIFT 算法是特征點匹配領域中具有里程碑意義的算法, 但SIFT 算法構建128 維特征向量降低了運算速度。 而SURF 算法在匹配速率上有所提升,是對SIFT 的改進算法,為算法在實時計算機視覺系統中應用提供了可能[1]。
除此,由于受拍攝或環境等問題,可能會出現圖像亮度不均、對比度低、噪聲多等情況,為后續研究帶來不便。 SURF 特征匹配在光照良好的情況下匹配效果很好,當光照不足或曝光過度情況下匹配不足。 利用圖像增強技術對圖像進行預處理,使圖像中物體與背景之間的對比度更強,突出圖像中的某一部分, 使得這一部分的細節變得更加清晰,從而有利于更進一步的觀察與分析。
在上述基礎上, 本文提出將圖像增強技術與SURF 算法相結合的思想, 預先使用不同的圖像增強方法進行處理,通過實驗驗證結合圖像增強技術后的SURF 算法對特征提取與匹配的改善[2]。
1 SURF 算法原理
相比于SIFT 算法,SURF 算法更快且魯棒性更好。 因為該算法在保證正確匹配的前提下做出了相應的簡化,同時多次采用積分圖像,因其計算簡單且根據積分圖像易得到圖像任何矩形域灰度值,大大的提高了效率。并且采用Haar 小波變換增加魯棒性[3]。
1.1 局部特征點提取
1.1.1 構建Hessian 矩陣
通過構建Hessian 矩陣生成圖像穩定的邊緣點,從而為特征提取做基礎[4]。 一副圖像f(x,y),其Hessian 矩陣可表示如下:
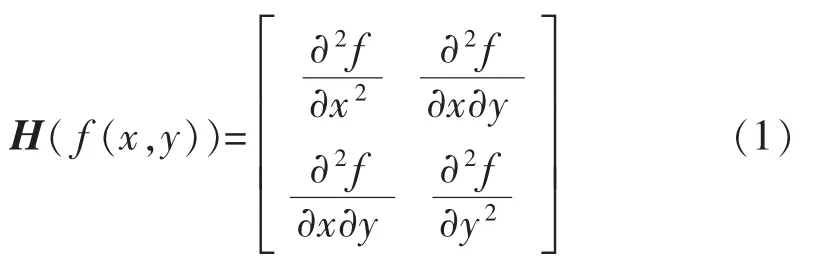
在構建矩陣前需要對圖像進行高斯濾波,經濾波后的Hessian 矩陣為
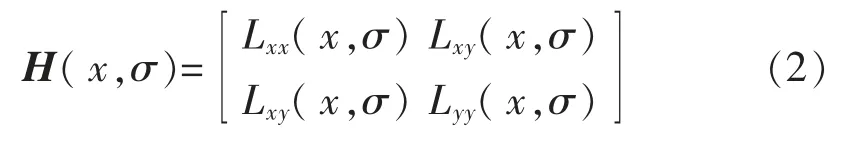
通過Hessian 矩陣的判別式定位關鍵點位置。當取得局部極大值時,判定當前點是比周圍鄰域內其他點更亮或更暗的點[3]。
1.1.2 構建尺度空間
構建圖像尺度空間,是指從不同尺度上對圖像特征進行檢測,目前比較好的方法是通過建立圖像金字塔對圖像進行多尺度描述。 傳統方法使用生成的高斯金字塔中同組的上層圖像減下一層,從而獲取高斯差分圖像,依賴上層結果,高斯模板不變但是改變圖像大小,降低運算效率。 而在SURF 中,依靠盒式濾波器而非高斯模板,因此可以不改變圖像的大小,僅通過改變盒式濾波器的模板尺寸來實現尺度不變性, 同時提高了算法速度和精度。 如圖1所示。
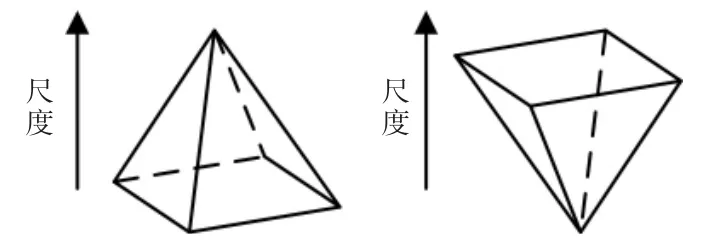
圖1 金字塔結構Fig.1 Pyramid structure
1.1.3 特征點定位
此過程共分3 個步驟:選取閾值、進行非極大值抑制以及插值。
首先選取閾值,保留最強的響應值,當選擇的閾值越大則特征點越多。 然后式非極大值抑制,將經Hessian 矩陣處理的每個像素點與尺度空間的8個鄰域像素比較,還要與鄰近尺度空間的分別9 個鄰域像素比較,共26 個像素點,不包括第一層與最后一層圖像,如圖2 所示。 最后通過泰勒級數來進行插值計算,初步定位出關鍵點,過濾掉定位錯誤或者能量差的關鍵點進而篩選出穩定的特征點[4]。
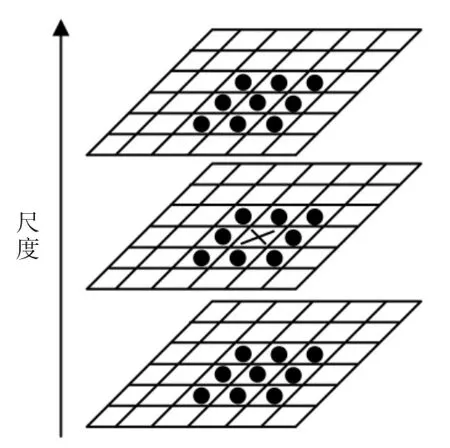
圖2 特征點定位Fig.2 Feature point positioning
1.1.4 特征點主方向分配
SURF 算法中,采用特征點鄰域內的Haar 小波特征。 以特征點為中心,計算半徑為6 s 圓形區域響應, 計算60°扇形范圍內所有點的水平和垂直特征響應之和,形成新的矢量,遍歷整個圓形區域,最后將最長的新矢量方向作為該特征點的主方向[4]。 該過程示意圖如圖3 所示。
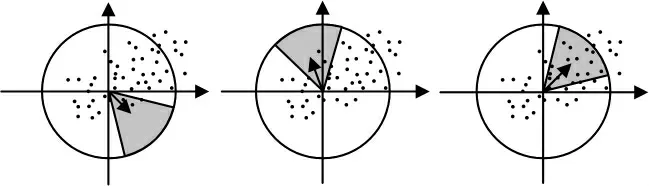
圖3 特征點主方向求取過程Fig.3 Feature point main direction seeking process
1.2 生成特征點描述子
在SURF 算法中, 在特征點附近沿主方向采用4×4 矩形塊。 計算各個子區域內25 個像素的Haar小波特征。 這4 個值分別為各個子塊區域的特征向量,因此SURF 特征描述子共64 維向量,其比SIFT特征描述子小2 倍[5]。
1.3 特征點匹配
通過計算2 個特征點間的歐式距離來確定匹配度,歐氏距離越短,代表2 個特征點的匹配度越好。 通過Hessian 矩陣跡的判斷,如果2 個特征點的矩陣跡正負號相同,代表這2 個特征具有相同方向上的對比度變化,如果不同,說明這2 個特征點的對比度變化方向是相反的,即使歐氏距離為0,也直接予以排除[4]。
2 RANSAC 精匹配
RANSAC 算法中指出,有效數據稱之為“內部點”, 即有效數據的分布可以用一定的模型參數來解釋,而不能契合該模型的無效數據則稱之為“外部點”。 利用內部點數據對參數進行估計,以便刪除不準確的數據。 此過程需用迭代方式估計參數。
為改進SURF 特征點之間的匹配正確率, 選擇RANSAC 算法來對匹配點進行篩選。 選擇內點數量最多時對應的變化矩陣為最佳估計變換矩陣,同時相應的內點即為提純后的匹配點對[6]。
3 圖像增強算法
圖像增強是指有目的增強圖像有用信息,改善圖像質量,加強效果。 使處理后的圖像比原始圖像更適用。 本文使用Gamma 變化、直方圖均衡化以及圖像銳化等方法來進行圖像增強處理,并利用曝光不足或過曝光的情況驗證各種方法的適用場合。
3.1 Gamma 變換
Gamma 變換可以對圖像進行矯正[7],適用于曝光不足或者過曝光的圖片, 可以增強圖像的對比度。 Gamma 變換的公式如下:
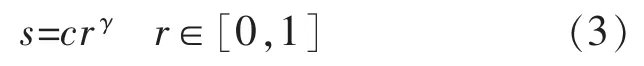
一般情況下,Gamma 變換是通過改變伽馬值,來對高光部分或暗調部分擴展,以增強這些部分細節。 經Gamma 變換后的關系圖如圖4 所示。
Gamma>1 時,亮區灰度拉伸,暗區灰度壓縮,整體圖像變暗;

圖4 輸入輸出灰度值關系Fig.4 Input and output gray value relationship
Gamma<1 時,亮區灰度壓縮,暗區灰度拉伸,整體圖像變亮。
3.2 直方圖均衡化
對于圖像灰度值分布過于集中的情況,直方圖均衡化可將圖像灰度概率分布變均勻,使圖像的直方圖盡可能的平穩。 變換如下:

變換函數T(r)與原圖概率密度函數的關系為
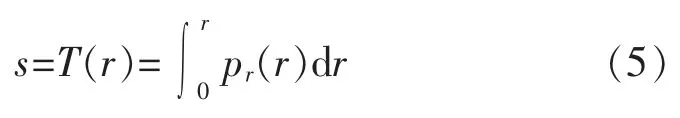
離散形式如下:
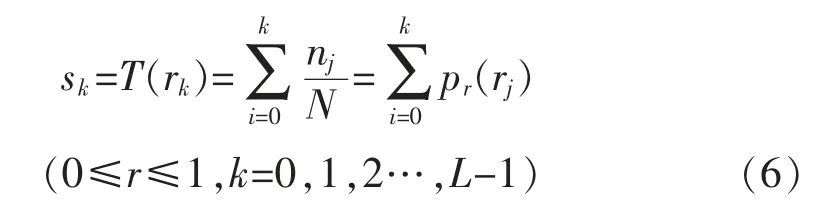
經多次變換得到均衡化處理的圖像。
3.3 圖像平滑
圖像噪聲是指圖像中不必要的或者多余的干擾信息,表現形式為在圖像中形成突變效果的一系列孤立的像素區域,干擾圖像的可觀測信息。 圖像平滑從信號處理的角度看就是去除其中的高頻信息,保留低頻信息,從而達到減少圖像中噪聲的目的[8]。
3.4 拉普拉斯算子法
拉普拉斯算子又叫做二階微分線性算子,假設圖像為f(x,y),則其拉普拉斯算子為

將二階偏微分近似可得到用于圖像銳化的拉普拉斯算子:
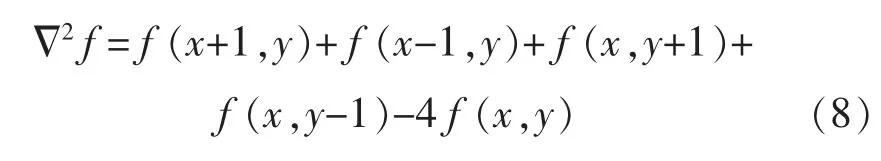
最終的銳化公式為
3.5 同態濾波
同態濾波對圖像灰度范圍進行調整,通過消除圖像上照明不均的問題增強暗區的圖像細節,同時又不損失亮區的圖像細節[9]。
一副圖像能用它的入射光分量和反射光分量來表示,關系式如下:
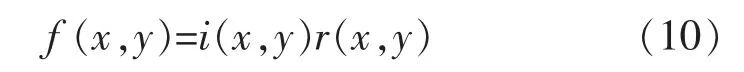
此方法要用同一個濾波器來實現對入射分量和反射分量的理想控制,關鍵是選擇合適的H(x,y),對圖像的低頻和高頻分量有不同的影響,因此稱之為同態濾波,如圖5 所示。
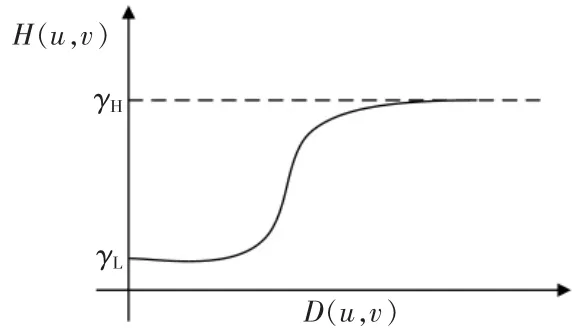
圖5 同態濾波器濾波函數的剖面Fig.5 Profile of the homomorphic filter function
4 算法實驗結果與分析
在自然條件下, 光照對采集圖像具有很大影響,不同光照條件可能導致圖像曝光不足或過曝光的情況影響質量, 為后續匹配等研究帶來不便,圖像增強技術是對圖像進行處理以提升圖像質量因此分別采用不同圖像增強方法來對質量缺陷的圖像進行處理, 進而再利用本文所改進的SURF 算法進行特征匹配,并用特征點數、匹配點數量、運行時間來衡量優劣。
首先選取2 幅曝光不足圖像實驗,見圖6、圖7及表1。

圖6 光不足原圖Fig.6 Underexposed original photo

圖7 光不足圖像匹配結果Fig.7 Underexposed image matching results
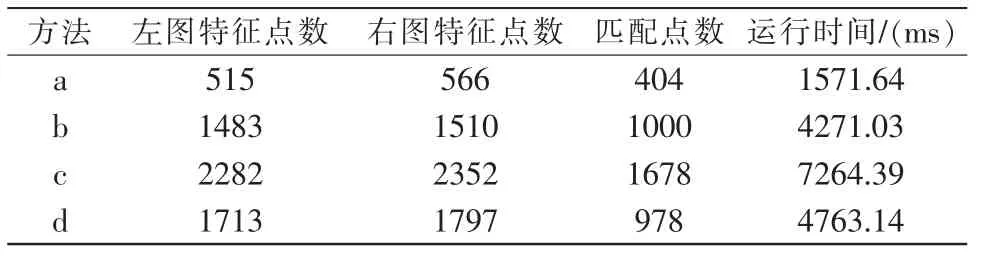
表1 光不足圖像匹配數據Tab.1 Underexposed image matching data
選擇2 幅過度曝光的圖像實驗,見圖8 及表2。
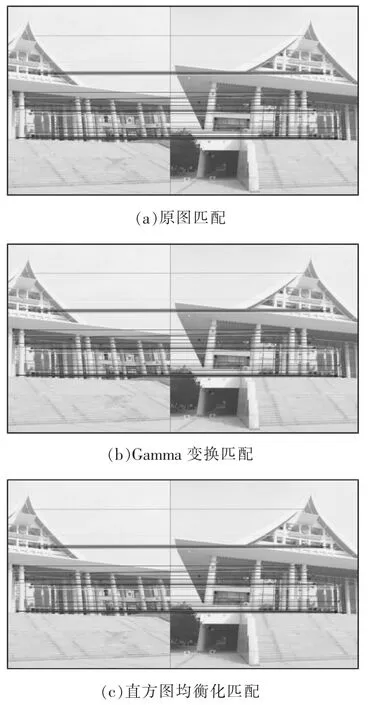
圖8 過度曝光圖像匹配結果Fig.8 Overexposed image matching results
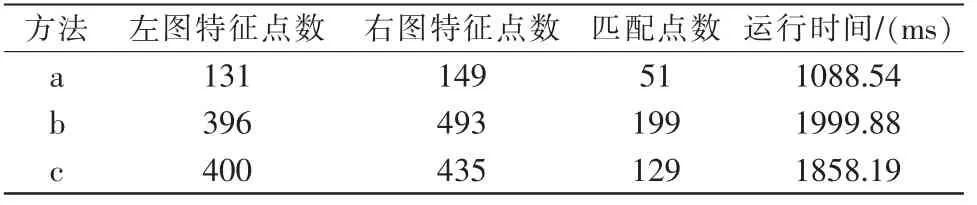
表2 過度曝光圖像匹配數據Tab.2 Overexposed image matching data
通過以上2 組由于光照影響導致曝光質量缺陷的圖像匹配實驗可以得出以下結論:
(1)使用多種圖像增強方法對圖像進行預處理后,各組圖像匹配點以及特征點數量均有提升。 較原圖匹配效果更佳;
(2)對于第一組曝光不足圖像采取拉普拉斯處理后效果最為顯著;直方圖均衡化特征點增加匹配點數增加少于其他增強效果;Gamma 變換效果較其他方法欠佳,且需要自行調整參數至合適亮度;
(3)對于第二組過曝光圖像采用拉普拉斯和同態濾波無效果,故選取了較為合適的兩種方法做對比,其中Gamma 變換匹配效果優于直方圖均衡化;
(4)采用各種圖像增強方法進行預處理均增加了消耗時間。 如何在提升匹配點數同時降低時間消耗有待進一步研究。
5 結語
隨著社會的發展,圖像匹配在各個領域也將得到越來越廣泛和深入的應用。
SURF 算法是對SIFT 算法的改進,作為常用的圖像匹配算法,仍將是研究的熱點和重點。 在存在光照影響圖像質量有缺陷時,SURF 匹配效果不好,將SURF 算法與現有的圖像增強算法結合, 可以大大提高特征點提取的數量和質量[10]。
本文介紹了SURF 算法基本理論并采用RANSAC算法來對匹配點進行篩選進而提高匹配正確率,提出將SURF 算法與現有的圖像增強算法相結合的思想, 先改善圖像質量再進行特征點的提取與匹配,使通過適當方法處理后的圖像匹配效果更佳。

