基于粒子群算法優化的城市供水量預測模型研究

陳攀 杜坤 周明 毛潤康 雷雨晴 丁榕藝

摘 要：鑒于BP神經網絡、RBF神經網絡在城市供水量預測精度上的不足，利用粒子群算法優化兩者相關參數，實現更高預測精度，并通過建立BP神經網絡、RBF神經網絡、PSO-BP神經網絡、PSO-RBF神經網絡分別對城市供水量數據進行仿真預測。最終測試樣本統計結果顯示：RBF神經網絡比BP神經網絡平均相對誤差（MRE）低約1%，在擬合度（R2）上高約0.014;PSO-BP神經網絡比BP神經網絡在MRE上降低約1.25%，在R2上提高約0.05;PSO-RBF神經網絡比RBF神經網絡在MRE上降低約0.3%，在R2上提高約0.072。由此說明RBF神經網絡比BP神經網絡在城市供水量預測方面更有優勢，并且利用粒子群算法優化神經網絡模型參數可有效提升神經網絡預測精度。

關鍵詞：粒子群算法;神經網絡;供水量;相對誤差;擬合度

DOI：10. 11907/rjdk. 191738 開放科學（資源服務）標識碼（OSID）：

中圖分類號：TP303文獻標識碼：A 文章編號：1672-7800（2019）007-0019-05

Research on the Prediction Model of Urban Water Supply

Based on Particle Swarm Optimization

CHEN Pan， DU Kun， ZHOU Ming， MAO Run-kang， LEI Yu-qing， DING Rong-yi

（Faculty of Civil Engineering and Mechanics， Kunming University of Science and Technology， Kunming 650500， China）

Abstract：In view of the shortage of BP and RBF neural networks in the prediction accuracy of urban water supply， the particle swarm optimization algorithm is used to optimize the related parameters to achieve higher prediction accuracy， and BP neural network， RBF neural network and PSO-BP are established. The neural network and PSO-RBF neural network respectively simulate and predict the urban water supply data. The final test sample statistics show that the RBF neural network is about 1% lower than the BP neural network average relative error （MRE）， and about 0.014 higher than the fitness （R2）; PSO-BP neural network ratio the BP neural network was reduced by about 1.25% on the MRE and about 0.05 on the R2; the PSO-RBF neural network was reduced by about 0.3% on the MRE than the RBF neural network， and the R2 was improved on R2 by 0.072. Therefore， it is shown that RBF neural network has more advantages than BP neural network in urban water supply forecasting， and using particle swarm optimization algorithm to optimize the parameters of neural network model can effectively improve the prediction accuracy of neural network.

Key Words： particle swarm optimization; neural network; water supply; relative error; fitting degree

基金項目：國家自然科學基金項目（51608242）;云南省應用基礎研究青年項目（2017FD094）

作者簡介：陳攀（1994-），男，昆明理工大學建筑工程學院碩士研究生，研究方向為市政工程;杜坤（1986-），男，博士，昆明理工大學建筑工程學院講師，研究方向為智能優化算法、供水管網數值仿真等。本文通訊作者：杜坤。

0 引言

城市供水量預測在水廠水泵運行與優化調度中起著舉足輕重的作用。準確可靠的供水量預測可提高市政供水管網穩定性與可靠性，并降低運行時產生的能耗，同時也是城市供水基礎設施規劃設計的關鍵[1]。

神經網絡模型是近年研究熱門，也是預測城市供水量的有效模型，但由于其中參數設置直接影響模型性能和預測精準度等，往往需要反復調試各個參數尋找最優參數設置，而粒子群算法（PSO）能夠利用自身算法特點將神經網絡中的某些參數進行優化，因此可以得到更優越的神經網絡模型用于供水量預測。

班懿根[2]利用RBF神經網絡對阿克蘇市需水量進行預測，預測結果與實際需求吻合度較高，但當原數據不充分時，預測精度較低;溫家鳴等[3]利用BP神經網絡對桂林市需水量進行預測，精確度較高，但該神經網絡易陷入局部最優解。

針對以上神經網絡的缺點，許多學者利用粒子群算法進行參數優化：張志宇等[4]利用粒子群算法優化RBF神經網絡參數，再對需水量進行預測，模型運行速度及預測精度得到了提升;徐瑾等[5]為了解決BP易陷入局部最優解的問題，利用粒子群算法優化BP網絡連接權值及閾值，結果顯示優化后的模型預測精度更高、更穩定;陳偉楠等[6]將主成分分析法、粒子群算法及BP神經網絡相結合對泰州市供水量進行預測，結果顯示該組合運行速度快、預測精度更高;商志根等[7]利用粒子群算法確定LS-SVM模型相關參數，相比于原模型，優化后的模型預測精度更高。

本文利用粒子群算法優化BP神經網絡與RBF神經網絡相關參數，并對某市供水量數據進行仿真預測，對比分析預測結果可知，該算法不僅可比較兩者性能差異，還可對神經網絡進行優化，克服神經網絡應用的部分難點。

1 神經網絡模型

1.1 RBF神經網絡

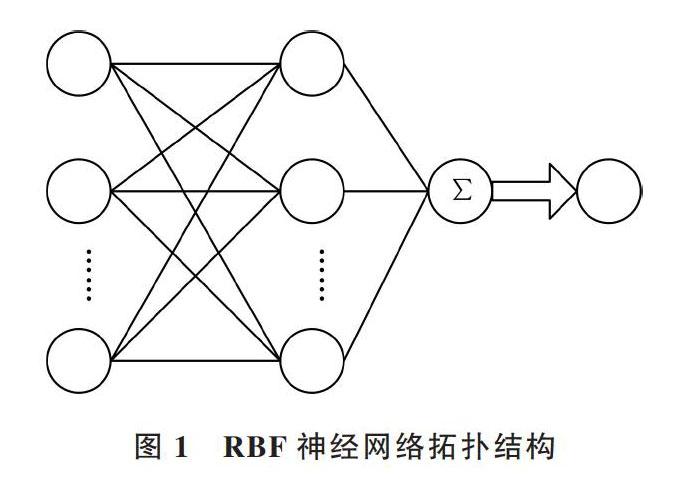
徑向基（RBF）神經網絡[8]是一個三層前向神經網絡，具有一個單獨隱層。如圖1所示，第一層為輸入層，輸入層由信號源節點組成，僅用于傳輸信號;第二層是隱含層，利用非線性優化方法對輸入向量進行變換，并將低維輸入數據轉換為高維空間，使低維空間非線性問題成為高維空間線性問題;第三層是輸出層，使用線性優化策略調整線性權重。

圖1 RBF神經網絡拓撲結構

激活函數（徑向基函數）[9]可表示為：

[R（Xi-Zi）=exp（-12σ2Xi-Zi2）]? ? ? ? （1）

網絡輸出[10]可表示為：

[Yi=i=1hWijexp（-12σ2Xi-Zi2）]? ? ? ? （2）

其中，[Xi]指第i個輸入樣本，[Zi]指隱藏層單元中心，[σ]指寬度，h指隱含層節點數，n指輸出的樣本數，W指隱含神經元至輸出神經元的連接權值。

RBF應用難點在于網絡訓練，網絡訓練應正確選擇和估計輸入參數，包括基本功能的中心和寬度以及神經元連接權重。RBF神經網絡隱含層至輸出層的映射關系是線性的，而將向量由低維度映射至高維度就是隱含層的作用，由此在高維度中就變成線性可分。RBF網絡在非線性與線性之間變化，使網絡加快學習速度且避免陷入局部極小解的情況;預測模型中的特征預處理技術對預測精度也有顯著影響，尤其是將神經網絡與預處理的輸入特征數據相結合，可以獲得更好的預測精度。

本文利用MATLAB中的newrb函數進行建模。建模前需要預先設定訓練參數，包括徑向基函數擴展速度和均方誤差目標。速度越大，函數逼近誤差越大，但低速會導致網絡性能下降。目標用于控制訓練過程的終止。在訓練過程中，中間層神經元數量不斷增加，直至模型均方誤差達到設定值（目標）。由于很難確定這兩個參數的最佳值，本文利用PSO優化網絡中的最佳訓練參數（W，Z，σ 3個參數）使神經網絡性能大幅提升。

1.2 BP神經網絡

反向傳播神經網絡[11]（BP神經網絡）是一種多層前饋人工神經網絡，由Rumelhart & McCelland于1986年提出的誤差反向傳播算法訓練而成。BP神經網絡能夠在數據輸入前后學習和存儲大量功能關系，若沒有事先確定功能關系，只能通過數據訓練。BP神經網絡算法是一種監督學習算法，即若輸出層的實際輸出值與期望的輸出值不匹配，將立即進行誤差反向傳播。該算法基于最小二乘法（LMS），采用逐層向前移動的方法，使輸出值與期望值之間的誤差平方在閾值范圍內。換言之，BP神經網絡通過反向傳播修正網絡權值和閾值，減小輸出值和期望值之間的誤差。BP神經網絡結構包括輸入層、隱含層以及輸出層。

圖2 BP神經網絡拓撲結構

隱含層節點輸出[12]為：

[Oj=f（∑Wij×Xi-qj）]? ? ? ? （3）

輸出節點輸出模型[13]為：

[Ym=f（∑Wjk×Oj-qk）]? ? ? ? （4）

其中，[Oj]指隱含層節點輸出，f指非線性作用函數，[Wij]及[Wjk]指隱含層連接權值，[Xi]指輸入值，[Ym]指輸出值，[qj]及[qk]指神經單元閾值。

其中，PSO算法優化對象是BP神經網絡中的W和q兩個參數。

考慮到將數據歸一化后可大幅提高神經網絡性能，因此本文利用式（5）對原數據進行線性函數轉換，再進行歸一化處理。

[y=x-xminxmax-xmin]? ? ? ? ? （5）

其中，y指神經網絡輸出值;x指原始數據輸入值;[xmin]指原始數據中的最小值;[xmax]指原始數據中的最大值。

BP神經網絡具有網絡結構簡單、可操作性強、輸入輸出任意非線性擬合等優點，可用于圖像識別、信息預測和模式識別等。

由式（6）可以大致確定BP神經網絡的隱含層神經元個數最佳值范圍[14]。

[h=（m+n）+a]? ? ? ? ? （6）

其中，h指隱含層神經元個數，m指輸入層節點數，n指輸出層節點數，a指1～10的常數。

2 粒子群算法

粒子群優化（PSO）算法是Eberhart & Kennedy[15]于1995年提出的一種基于種群的隨機優化技術。PSO的發展靈感來自于動物群體的社會行為，如鳥群和魚群。PSO與其它一些進化計算技術有許多相似之處：系統由隨機解的總體初始化，并通過更新代數搜索最優解。在粒子群優化算法中，每個個體都被稱為一個粒子，其行為就像鳥群（魚群）中的一只鳥（或魚）在尋找食物或躲避捕食者。每個粒子都有一個位置和一個速度，用來探索問題的搜索空間。一個位置代表一個潛在的問題解決辦法。一個粒子從它自己的經驗中學習（認知成分），也從群體中學習（社會成分）。通常，個人和社會成分分別稱為Pbest（個體極值）和gbest（全局最優）。為了評估一個解，PSO迭代地計算每個粒子的適應度[16]。

這些粒子在超大型搜索空間中“飛行”。搜索空間中粒子位置變化是基于個體的社會心理激勵原理。每個粒子的位置根據其經驗和相鄰粒子的經驗變化。粒子群算法中的粒子作為候選解被引入。粒子執行迭代目的是找到具有目標函數最佳值的解。每個粒子都有一個由矢量[Xi]（其中，i是粒子的下標）表示的位置，速度則表示為[Vi]矢量。迭代過程中的每一個粒子均會記住自身在Pbest矢量中的最佳位置。粒子群中的最佳位置矢量存儲在gbest中。每次迭代時速度矢量的更新根據公式（11）進行;然后，利用前一位置獲得新的速度，根據公式（12）形成新的位置。

具體過程為：設在一個Z維空間里面，存在隨機粒子N個，則第i個粒子的位置函數可表示為[17]：

[Xi=（Xi1，Xi2，？，XiZ）]? ? ? ? ? ? （7）

其中i=1，2，……N（下同）。

第i個粒子速度為：

[Vi=（Vi1，Vi2，？，ViZ）]? ? ? ? ? （8）

第i個粒子目前尋找到的個體極值為[18]：

[Pbest=（Pi1，Pi2，？，PiZ）]? ? ? ? ?（9）

則該Z維空間中的整個群落（粒子群）尋找到的最優位置即為全局極值，因此可由式（6）表示為：

[gbest=（Pg1，Pg2，？，PgZ）]? ? ? ? （10）

其中，粒子依據公式（11）、（12）更新自己的速度及所在位置[19]：

[ViZ=wViZ+c1r1（PiZ-XiZ）+c2r2（PgZ-XiZ）]? ?（11）

[XiZ=XiZ+ViZ]? ? ? ? ? （12）

其中，[c1、2]為學習因子[20]（加速常數），[w]為慣性因子，[r1、2]指0～1的均勻隨機數。

算法具體步驟[21]如下：

Step1：設置好粒子群各項參數并且需要將各個粒子的位置及速度進行初始化。

Step2：計算各個粒子適應度值。

Step3：如果個體極值小于由Step2計算得到的適應度值，則使用適應度值替換掉個體極值。

Step4：如果全局極值小于Step2計算得到的適應度值，則會使用適應度值替換掉全局極值。

Step5：各個粒子根據式（11）及式（12）更新自己的速度以及位置。

Step6：粒子群算法會在達到停止條件時，停止繼續尋找最優值，否則算法將會返回Step2。

當達到程序設置的最大迭代次數或找到整個群落（粒子群）尋找到的最佳位置，即全局極值[gbest]時停止粒子群算法。

3 數據準備

本文采用收集到的某城市日供水量數據（不考慮其它影響因素），數據范圍由2004年1月1日-2005年2月3日，共計400個數值，并利用前5天的供水量值預測第6天的供水量值，若輸入矩陣記為P，輸出矩陣記為Y，第i天的供水量記為[Xi]，則可得：

P=[X1X2X3X4X5X2X3X4X5X6？？？？？X395X396X397X398X399]，Y=[X6X7？X399X400]

其中，本文將輸入矩陣前365行數據作為網絡訓練數據，第366行-第395行數據共30行數據作為測試數據，輸出矩陣前365行數據作為網絡訓練數據，第371行-第400行數據共30行數據作為網絡測試數據。

4 模型構建

本文通過建立BP、RBF以及由PSO分別優化的兩個神經網絡進行模型訓練及仿真測試。其中粒子群算法參數設置如下：C1=C2=2，迭代次數設為200次，種群規模設置為30，粒子最大速度取1，最小速度取-1，最大權值取0.9，最小權值取0.2，訓練誤差設為1e-9。算法達到設置最大迭代次數或達到設置訓練誤差時即停止尋找最優值。

4.1 仿真結果

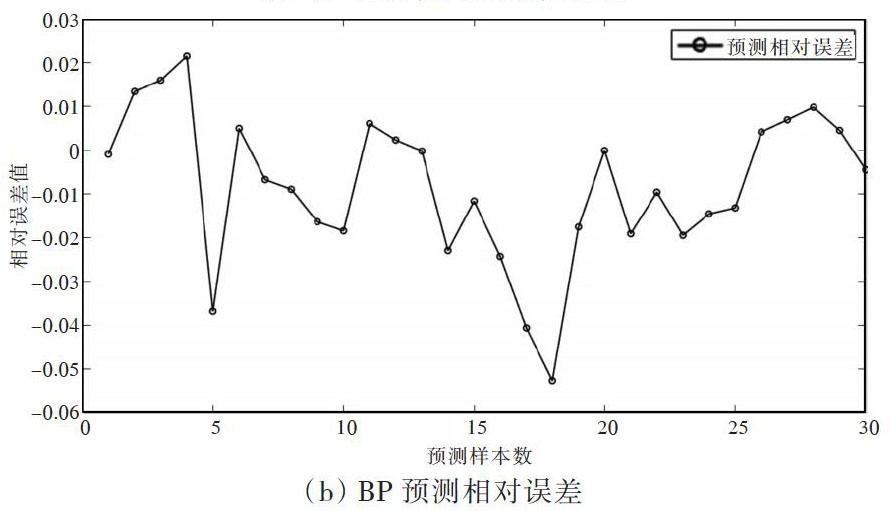
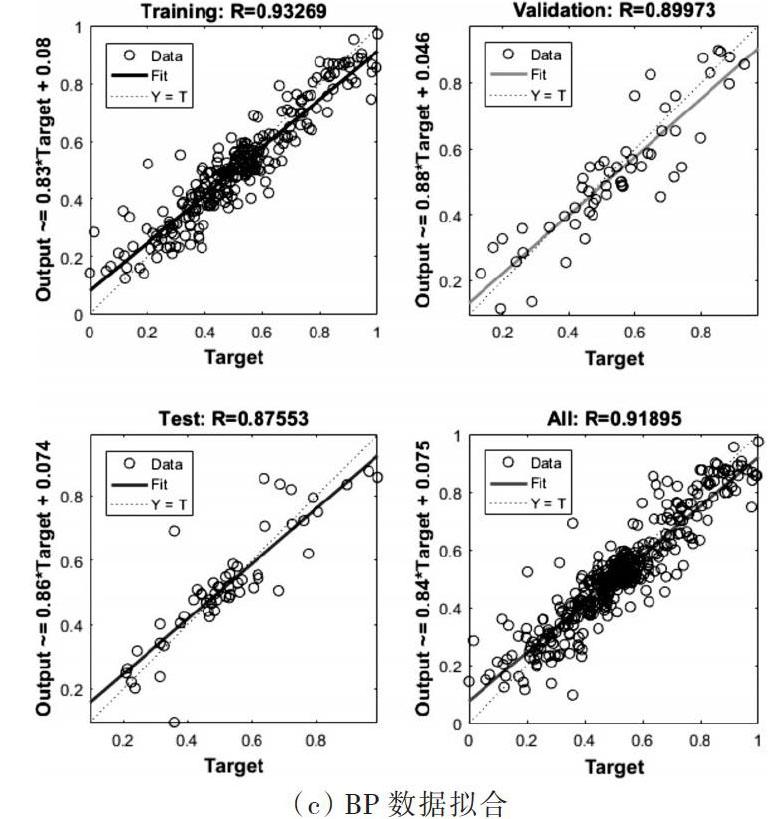
本文使用Matlab2016b軟件進行模型訓練以及仿真預測，分別建立BP、RBF、PSO-BP、PSO-RBF4種神經網絡模型，預測得到的各項指標情況如圖3及表1所示。

圖3 各神經網絡各項指標

圖3中的數據擬合圖為訓練數據、驗證數據、測試數據及所有數據擬合度，從中可以反映模型訓練程度是否充分、模型是否可靠、有無過擬合等異常情況。由圖3可知，本文建立的4個神經網絡模型均為可靠有效的模型。

表1 相關指標統計結果

5 結語

本文使用粒子群算法對RBF與BP神經網絡的相關參數進行優化，再利用MATLAB軟件進行仿真模擬，最后對比優化前后神經網絡的預測精度、預測誤差、擬合度等指標。實驗證明，粒子群算法能夠提升神經網絡的預測精度與擬合度，減小預測誤差。但通過粒子群算法優化后的神經網絡在預測精度方面仍有提高空間，這是下一步研究重點。

參考文獻：

[1] 郭冠呈，劉書明，李俊禹，等. 基于雙向長短時神經網絡的水量預測方法研究[J]. 給水排水，2018，44（3）：123-126.

[2] 班懿根. 基于RBF神經網絡的城市需水量預測[J]. 地下水，2012，34（1）：114-116.

[3] 溫家鳴，郭純青，李新建， 等. 基于BP神經網絡的桂林生態城市建設需水量預測[J]. 水資源保護，2012，28（3）：47-50.

[4] 張志宇，趙丹國，侯曉宇. PSO-RBF神經網絡在城市需水量預測中的應用[J]. 水電能源科學，2013，31（6）：55-57.