基于FPGA的磁定位技術研究與實現

成龍 鄭建立

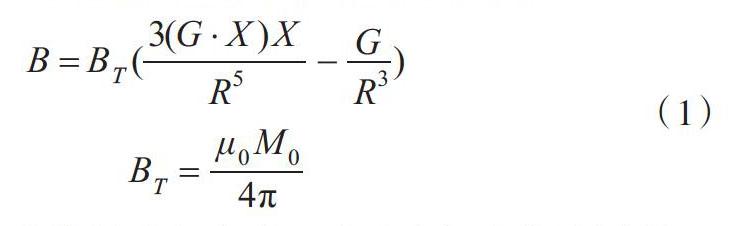
摘 要：在磁定位技術應用過程中，為解決數據處理過程復雜、計算量大導致實時性無法滿足問題，利用FPGA的并行結構，設計實現了一種基于FPGA平臺的磁定位方案。實驗結果表明，磁矩為0.1255[A？m2]的永磁體在距離磁傳感器高度在20cm以內時，定位精度能達到毫米級，定位速度比通用計算機提升了一倍以上，可以滿足絕大多數實時性要求，更有利于永磁體定位技術產業化，應用前景廣闊。

關鍵詞：磁定位技術;數據處理;實時性;FPGA;定位精度

DOI：10. 11907/rjdk. 182679 開放科學（資源服務）標識碼（OSID）：

中圖分類號：TP319文獻標識碼：A 文章編號：1672-7800（2019）007-0145-05

Research and Implementation of Magnetic Positioning Technology Based on FPGA

CHENG Long， ZHENG Jian-li

（School of Medical Instrument and Food Engineering， University of Shanghai for Science and Technology， Shanghai 200093， China）

Abstract： In the process of applying magnetic positioning technology， the complicated data processing and the large calculation amount often lead to that the real-time requirement cannot be met.In order to solve this problem， based on the parallel structure of FPGA， this study designs and implements a magnetic positioning scheme， including data acquisition，data processing and data output.The results show that the positioning accuracy can reach millimeter level when the height of the magnet with a magnetic moment of 0.1255[A？m2] is within 20 cm from the magnetic sensor. Moreover， the positioning speed of the scheme is more than double that of using the general computer， which can satisfy most real-time requirements.It is more beneficial to the commercialized development of magnetic positioning technology and has broad application prospects.

Key Words： magnetic positioning technology; data processing; real-time; FPGA; positioning accuracy

基金項目：上海市科委科技支撐項目（17-C-2）;上海理工大學微創勵志創新基金項目（YS30810128）

作者簡介：成龍（1994-），男，上海理工大學醫療器械與食品學院碩士研究生，研究方向為醫學儀器嵌入式技術;鄭建立（1965-），男，博士，上海理工大學醫療器械與食品學院副教授、碩士生導師，研究方向為醫學信息系統與集成技術、醫學儀器嵌入式控制系統。本文通訊作者：鄭建立。

0 引言

磁定位技術是目前應用較為廣泛的定位技術之一，適用于空間較小、無磁干擾的場景，具有定位精度高、成本較低等優點。磁定位技術分為電磁定位技術和永磁定位技術[1]。電磁定位技術主要由磁場發射源、磁場接收、數據處理3部分組成。向三軸線圈通入交流或直流脈沖信號，線圈周圍產生的感應磁場作為磁場發射源。磁傳感器作為磁場接收裝置，對采集到的信號進行處理得到六維數據[2]。電磁定位技術的優點是不受視線阻擋，缺點是采用直流或低頻電流作為激勵，控制電路伴有能耗，環境中的鐵磁性物質會造成電磁場畸變從而影響精度。永磁定位技術由永磁體、磁傳感器陣列、數據處理3部分組成。通過高精度的磁傳感器組成的傳感器陣列，采集永磁體的三軸磁感應強度值，然后將采集到的三軸數據進行定位算法處理，得到磁體在空間中的三維坐標。永磁體定位技術優點在于無需供電和控制電路，無需激勵電流。現階段永磁體多采用強磁材料釹鐵硼制成，具有體積小、磁性強的特點，使永磁定位技術信號源占用空間小，在微型化和功耗要求高的應用環境中優勢明顯。

永磁體定位技術研究很多，如侯文生等[3]建立了一套針對消化道微型診查設備的定位系統，胡超等[4]提出了一種基于人工蜂群算法的定位方式，劉暢等[5]建立了一套膠囊內窺鏡弱磁場測量系統，任宇鵬等[6]修正了磁偶極子模型在近場不適用問題。以上研究在數據處理部分大多依賴Matlab和Labview等PC端軟件完成，處理速度較慢、實時性不夠。數據依賴PC處理不方便攜帶，難于產業化。

計算機數據處理往往是基于一種串行結構，而FPGA內部由LUT和FF構成，擁有豐富的時序邏輯資源，現在很多FPGA都集成了DSP和BRAM。因此，常常利用FPGA處理一些數據量較大、過程較為復雜的算法。將算法中的多個過程完全并行處理，在同一段時間內就能進行多路計算，大大加快了數據處理過程[7]。

1 磁定位原理

1.1 磁偶極子模型

磁偶極子模型廣泛應用于目標物體的定位和狀態測定中。當目標磁體的體積遠遠小于檢測距離時，該物體可看作磁偶極子。磁偶極子是最小的磁單元，它是類比電偶極子而建立的模型[8]，由大小相等、方向相反的兩個點磁荷構成系統。自然界有許多磁現象可以視為一個磁偶極子，比如一根小的磁針。

磁偶極子模型中磁感應強度計算公式如下：

[B=BT（3（G？X）XR5-GR3）BT=μ0M04π]? ? ? ?（1）

其中，[M0]是磁體的磁矩大小，可通過實驗直接測得已知量。[μ0]是空間中的磁導率，為一個已知量[9]。[G]是磁矩的單位方向向量，可表示為：[G=[sin？cosφ，sin？sinφ，][cos？]T]。其中，[？]和[φ]是未知量，[？]為[G]與Z軸正方向的夾角，[φ]為[G]在XY平面上的投影與X軸正方向的夾角[10-11]。[X]是磁體到磁傳感器的矢徑。假設永磁體在空間中的坐標為[[a，b，c]]，這是個未知量，磁傳感器在空間中的坐標為[[x0，y0，z0]]，是已知量，則[X=[x0-a，y0-b，z0-c]T]。[R]是磁體到磁傳感器的距離，上述磁感應強度計算公式中有5個未知的待優化參數，分別是[a，b，c，？，φ]。

1.2 定位算法原理

磁定位的最終目標是找到磁體在空間中的三維坐標和角度信息，相當于求解出這5個參數的最優解，使得最優解所對應的磁感應強度計算公式的函數值最接近磁體在空間中的真實磁感應強度。因此，需要通過分辨率較高的磁傳感器測量磁體在空間中的真實磁感應強度。未知參數有5個，而每個磁傳感器只能提供3個關系式。從解方程的角度看，至少需要兩個磁傳感器才能求出5個未知參數的解，這就是為何需要磁傳感器陣列而不是單個磁傳感器測量磁感應強度的原因。磁傳感器數量越多，所能提供的約束條件也越多，求解出的最優解就越精確。

求解最優解的過程其實是一種參數優化過程，所以需要用到最優化算法。常見的最優化算法有牛頓法、高斯—牛頓法、梯度下降法和L-M算法等。牛頓法是最早應用的優化算法之一，缺點在于只適用于變量是一維的情況。高斯—牛頓法和梯度下降法在牛頓法的基礎上加入了Hessian矩陣，用Hessian矩陣表示高維的求導函數，可以處理多維變量[12]。L-M算法又在梯度下降法和高斯—牛頓法基礎上引入一個加權因子，記為λ。該加權因子的作用是控制接近最優解的速度。若速度太快，就使用較小的λ，使L-M算法更接近高斯—牛頓法。若速度太慢，就使用較大的λ，使L-M算法更接近梯度下降法[13]。加權因子的加入在增加L-M算法靈活性的同時，也讓L-M算法兼備了高斯—牛頓法和梯度下降法的優點，這是L-M算法能快速收斂到全局最優解的重要原因[14]。

式（2）是L-M算法的迭代公式，其中[H（xn）]代表Hessian矩陣，[？f（xn）]代表殘差函數的梯度，λ代表加權因子。

[xn+1=xn-（H（xn）+λ？diag（H（xn）））-1？？f（xn）]? ? ?（2）

根據式（2）可知，L-M算法作為一種迭代優化算法，在每一次迭代步長的求解中都需要經過以下幾個步驟：①求Hessian矩陣和加權因子λ;②將Hessian矩陣的對角線元素加權;③對上一步處理完的結果求逆，并與殘差函數的梯度相乘。

具體的L-M算法參數優化過程為：①給5個參數分別賦一個初值，將它們代入磁感應強度計算公式中，得到一個計算值，記為[B1];②通過磁傳感器陣列去采集永磁體在空間中的磁感應強度，記為[Bt];③如果磁傳感器的精度足夠高，就可認為測得的[Bt]是一個相對精確的值。一開始，[B1]通常是偏離[Bt]較遠的，通過多次迭代，不斷縮小[B1]和[Bt]的差值，直到兩者誤差小于設定的閾值，就可近似認為此函數中未知數的值即是最優解，也即所要定位的永磁體的坐標信息和角度信息。

2 總體方案

2.1 系統架構

本設計由數據采集、數據處理和結果輸出3部分組成，流程如圖1所示。數據采集部分主要通過FPGA的I/O模擬磁傳感器的IIC數據接口，對磁傳感器的內部寄存器進行讀寫操作。控制傳感器對永磁體的三軸磁感應強度進行測量，并在測量完畢后讀出數據，交給定位算法部分處理。數據處理部分采用Lenvenberg-Marquard算法（常簡稱為L-M算法）。最后將數據處理結果通過串口輸出，在PC端界面上顯示定位結果。

圖1 方案流程

2.2 數據采集部分

本設計采用的磁傳感器是Maxim公司的各向異性磁阻傳感器MMC5883MA。各向異性磁阻傳感器的測量范圍以地球磁場分布范圍為中心，是最適合工作在地球磁場環境下的磁傳感器，其分辨率為0.25mGauss，量程為[±8]Gauss，最低采樣頻率為100Hz，A/D轉換精度為16bit，輸入輸出接口為IIC。其出色的性能可為軟硬件的抗干擾修正提供更為快速的算法，帶來更為精確及快速的方向定位。

該傳感器集成了IIC的數據接口，用戶可通過該接口配置傳感器的內部寄存器，從而控制傳感器測量永磁體的三軸磁感應強度，并在測量完成后讀出測量數據。

磁傳感器的控制過程如圖2所示。每次上電后都需要對傳感器進行置位和復位操作，隨后等待大約1～2ms，接著給傳感器發送測量指令，然后再等待10ms時間就可從傳感器的內部寄存器中讀取有效測量數據。若要進行連續測量，可在讀完數據之后立刻發送再次測量指令，但每次都需要等待10ms之后才能讀到有效數據。

圖2 磁傳感器控制過程

2.3 數據處理部分

數據處理部分涉及的L-M算法各功能模塊如圖3所示。該算法的實現分為目標函數值計算塊、Hessian矩陣生成塊、矩陣求逆塊、加權因子λ計算塊、迭代控制塊和矩陣乘法塊幾個部分。

目標函數計算塊中的目標函數是磁偶極子模型中磁感應強度計算公式，該計算塊的輸入值由兩部分組成：①數據采集模塊輸出的永磁體三軸磁感應強度，即為圖3中的測量值;②每個待優化參數的初始值，該初始值可任意給定。經過目標函數計算塊之后，得到測量值與計算值的殘差函數及方差和。迭代控制塊根據方差和是否小于閾值判斷迭代是否繼續。若方差和小于設定閾值則迭代完成，大于閾值則迭代繼續。在迭代繼續的情況下，Hessian矩陣生成塊和加權因子計算塊會同時工作，分別計算Hessian矩陣和加權因子λ，計算完成后將兩者同時作為輸入傳到矩陣求逆塊。矩陣求逆塊負責對角加權后的Hessian矩陣求逆，并將求逆后的矩陣、Hessian矩陣以及殘差函數一起傳到矩陣乘法塊，計算下次迭代的步長[dx]，并將初值與[dx]的差作為下次迭代的輸入值再次進行迭代，直到迭代完成。

圖3 L-M算法功能模塊

2.4 結果輸出部分

結果輸出部分將算法處理完成并輸出的數據通過串口傳給PC，并在PC端編寫串口接收界面顯示磁體的三維坐標和角度信息。其中，串口波特率為115200bps，1位停止位，8位數據位，無校驗位。串口輸出的數據幀格式如圖4所示，以0x02作為幀頭，緊接著輸出6個有效數據，每個有效數據都以4字節的ASCII碼表示。有效數據之后是CRC校驗碼，CRC校驗碼是4字節的ASCII碼，最后以0x03作為幀尾。

[0x02＼&X軸坐標值＼&Y軸坐標值＼&Z軸坐標值＼&弧度信息1＼&弧度信息2＼&迭代次數＼&CRC校驗碼＼&0x03＼&]

圖4 串口輸出的數據幀格式

3 數據處理模塊

3.1 Hessian矩陣生成塊

Hessian矩陣又稱為黑塞矩陣，是一個由多元函數的一階偏導和二階偏導構成的對稱正定矩陣[15]，描述了函數的局部曲率。黑塞矩陣最早由德國數學家Ludwig Otto Hesse提出，并以其名字命名。對于一個多元函數[f（x1，x2）]，黑塞矩陣的計算公式如下：

[H（x1，x2）=2i=1n（？fi？x1？fi？x2+fi？2fi？x1？x2）]? ? ?（3）

在Hessian矩陣中，由于計算復雜在L-M算法中常常省略二階偏導部分，僅對函數作一階偏導處理，硬件實現一階偏導同樣非常復雜。本設計采用有限差分法近似替代一階偏導。差分法是微分方程的一種近似數值解法，相當于用有限差分代替微分，用有限商分代替導數，因此求解微分方程的問題就轉換為求解代數方程問題[16]。在簡化運算提升效率的同時誤差也相對較小，以函數[f（x）]為例，[f（x）]的一階導數[f（x）]可用公式（4）表示。

[f（x）=f（x+h）-f（x）h]? ? （4）

3.2 加權因子λ計算塊

加權因子λ值的確定采用信賴域法，信賴域法基本思想是：先給定一個初始的λ值作為位移上界，以初始值點為圓心，以此位移上界為半徑所畫出的閉球區域作為信賴域區間，通過在此區間求解信賴域子問題的最優解得到一個位移量。若該位移有充分的下降，就保持或擴大該信賴域半徑，并且以位移后的新點作為圓心重新確定信賴域[17]。若該位移的下降不夠充分或者根本沒有下降則圓心不變，縮小信賴域，重新求解該信賴域子問題的最優解得到新的候選位移。如此重復下去，直到滿足迭代終止條件為止[18]。

本設計給定的降幅區間為[0.25，0.75]。所謂降幅即為實際下降量與預測下降量的比值，簡單說降幅的作用就是監督當前步長的質量。若當前降幅在區間內就滿足當前步長，保持目前的信賴域半徑不變，接受該步長。若當前降幅超出該區間則說明當前步長質量很高，可以接受該步長并擴大信賴域半徑再次迭代。若當前降幅小于該區間，說明當前步長質量不佳，就縮小信賴域重新進行搜索。

3.3 矩陣求逆塊

常用的矩陣求逆算法有LU分解法、QR分解法、Cholesky分解法等[19]。LU分解法適用于一切可逆矩陣的求逆，優點是具有普遍性，缺點是過程較為復雜，在硬件實現時消耗的邏輯資源較多，耗時也較長，效率不高。Cholesky分解法僅僅適用于對稱正定矩陣，普遍性不如LU分解法，優點是硬件實現時消耗的邏輯資源較少，耗時較短，效率較高[20]。

圖5為在Xilinx Zynq7020平臺上，分別采用Cholesky分解法與LU分解法設計5行5列64位矩陣求逆塊綜合后的邏輯資源用量對比，可以看出，Cholesky分解法所消耗的邏輯資源明顯少于LU分解法，LUT資源減少了22%，FF資源減少了10%，DSP資源減少了16%。

表1為兩個模塊分別對同一矩陣求逆所消耗的時間，可以看到，在同樣為50MHz的時鐘頻率下，采用LU分解法設計的求逆塊大約需要50.53μs才能完成一個5行5列矩陣的求逆，而采用Cholesky分解法設計的求逆塊僅需29.17μs即可完成，采用Cholesky分解法效率提升了大約42%。

因Hessian矩陣為對稱正定矩陣，所以本設計采用Cholesky分解法設計矩陣求逆塊。

表1 LU分解法與Cholesky分解法算法耗時比較? ? ? ? ?（μs）

圖5 LU分解法與Cholesky分解法資源消耗量對比

4 結果分析

測試實驗使用的永磁體類型為釹鐵硼永磁體，直徑為8mm，高度為3mm，磁矩為0.1255[A？m2]。

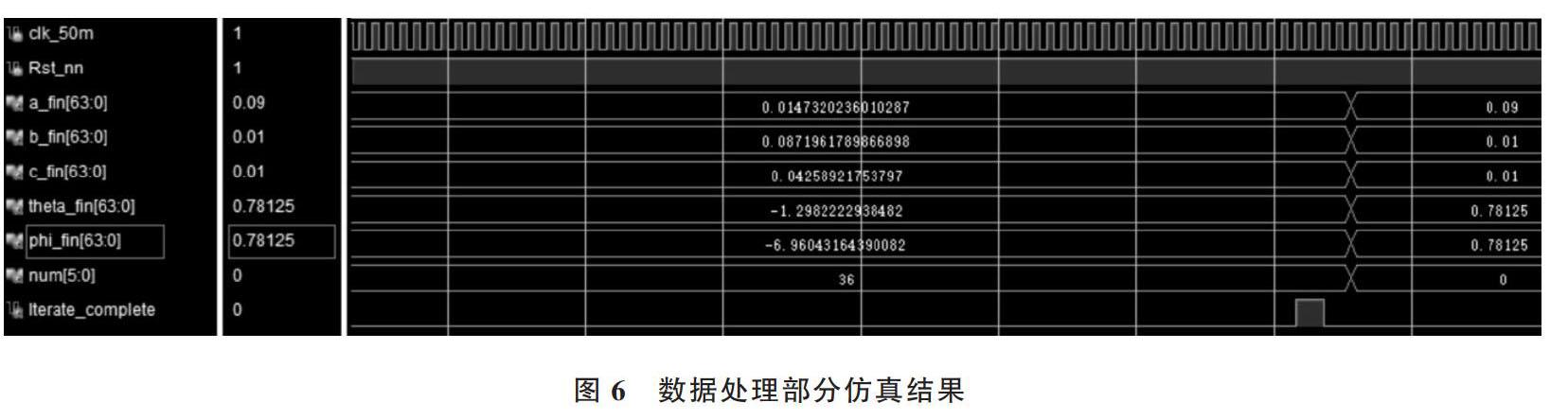
圖6是采用Xilinx公司的集成開發環境Vivado對數據處理的仿真結果，可以看到，最后迭代了36次完成了5個未知參數[a，b，c，？，φ]的優化。在迭代完成后，Iterate_complete標志位置為1，隨即輸出滿足迭代完成條件的最優解。

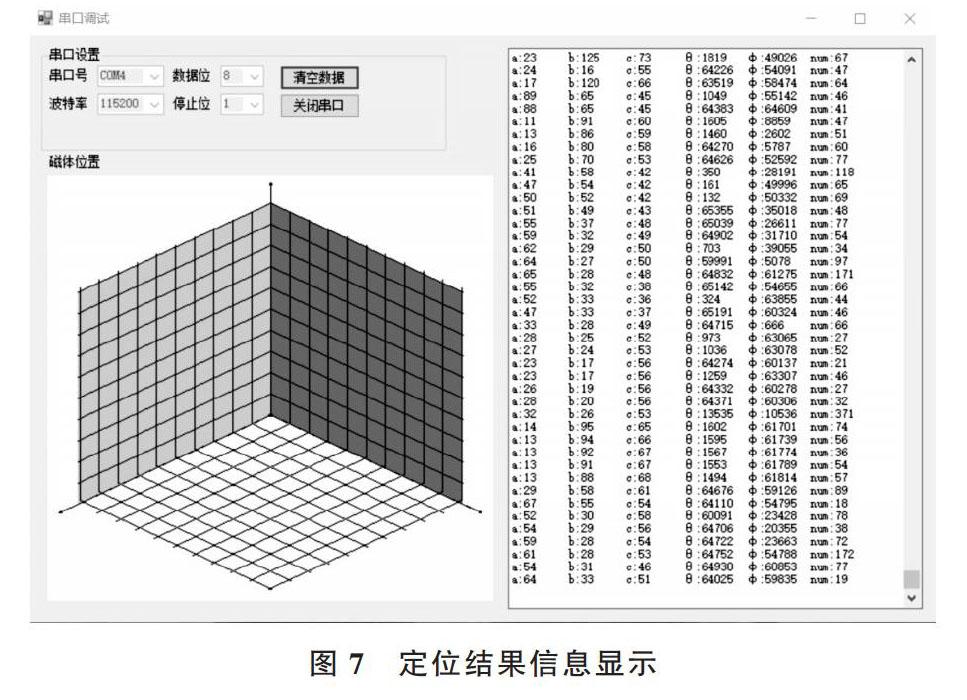
圖7是定位信息在串口接收界面上顯示的結果，以第一行數據為例：a：23 b：125 c：73 [θ]：1819 [φ]：49026 num：67。其中，23，125，73分別為X軸、Y軸和Z軸上的磁體坐標信息，單位為mm。隨后的兩個為磁體弧度信息，這兩個值均需除1 000并轉換到[-[π]，[π]]的區間內才有效。最后一個是迭代次數信息。

圖8是定位誤差統計，可以看到磁體距離傳感器的高度是影響定位誤差的重要因素。

當磁體高度在5cm左右時，平均定位誤差僅在3mm左右;當磁體高度在10cm左右時，平均誤差在5mm左右。隨著磁體高度的不斷增大，誤差也會隨之快速變大。當磁體距離傳感器的高度達到20cm以上后，定位誤差也增大到厘米級，這符合磁偶極子模型公式中磁感應強度與距離的三次方成反比的關系。

圖9是分別使用FPGA和通用計算機進行20次定位所得的耗時對比，圖中三角形點表示計算機的定位耗時，方形點表示FPGA的定位耗時。每次測試都給算法賦相同的初值，并且確保每次用兩者進行測試時磁體的位置保持不變，這相當于確保了所有外部條件不變，從而能客觀地比較兩者定位耗時的差異。可以明顯看出，FPGA在同樣條件下的定位速度比計算機快大約一倍以上。在處理5個參數的高次目標函數優化時，平均定位耗時僅6.034ms，遠低于計算機的平均定位耗時16.682ms，可以滿足大多數實時性要求較高的場景。

圖7 定位結果信息顯示

圖8 定位誤差統計

圖9 FPGA與通用計算機定位耗時對比

5 結語

本文描述了一種基于FPGA平臺的磁定位方案，利用FPGA并行結構快速采集和處理數據，完成定位工作。使用Xilinx公司的Vivado集成開發環境對該方案進行仿真，驗證該方案的正確性。最后將生成的bit文件下載到Xilinx Zynq7020開發板上，連接傳感器陣列，通過串口將定位結果在PC端接收界面上顯示。結果表明，在永磁體距離磁傳感器20cm以下時，定位誤差均在毫米級。與通用計算機進行數據處理方案相比，定位耗時縮短了一倍以上，取得了較為理想的定位效果。

本設計可有效解決磁定位過程中由于數據處理較為復雜且數據處理量大導致的數據處理時間較長問題，滿足大多數實時性要求。利用FPGA取代計算機進行數據采集和處理，有利于永磁體定位技術的產品化，應用前景良好。

參考文獻：

[1] 張可，湯福南，李修寒，等. 基于永磁定位技術的三維腿部運動檢測系統設計[J]. 中國醫療設備，2017（9）：33-39.

[2] 包建孟. 基于電磁跟蹤技術的室內移動機器人定位系統[D]. 寧波：寧波大學，2014.

[3] 候文生，鄭小林，彭承琳，等. 基于永磁體空間磁場檢測的體內微型診療裝置定位系統的研究[J]. 北京生物醫學工程，2004，23（2）：81-83.

[4] 鄭子昭，何小其，胡超. 基于人工蜂群算法的膠囊內窺鏡位姿磁定位研究[J]. 集成技術，2014（5）：52-60.

[5] 劉暢，劉修泉，黃平. 膠囊內窺鏡弱磁場測量系統設計與實驗研究[J]. 現代制造工程，2016（7）：95-100.

[6] 任宇鵬. 基于磁傳感器陣列的無線膠囊內窺精確定位技術[D]. 太原：太原科技大學，2016.

[7] 劉志成，祝永新，汪輝，等. 基于FPGA的卷積神經網絡并行加速結構設計[J]. 微電子學與計算機，2018（10）：80-84.

[8] 江勝華，侯建國，何英明，等. 基于磁偶極子的磁場梯度張量局部縮并及試驗驗證[J]. 中國慣性技術學報，2017（4）：473-477.

[9] 王延花. 基于磁阻傳感器的磁性納米顆粒檢測系統設計[D]. 南京：南京醫科大學，2014.

[10] WANG S S，GUO Q. Calculation and correction of magnetic object positioning error caused by magnetic field gradient tensor measurement[J]. Journal of Systems Engineering and Electronics，2018（3）：456-461.

[11] GAO X，LI B. A novel method of localization for moving objects with an alternating magnetic field[J]. Sensors（Basel），2017（4）：158-161.

[12] 王建梅，覃文忠. 基于L-M算法的BP神經網絡分類器[J]. 武漢大學學報：信息科學版，2005（10）：928-931.

[13] 申雅峰，張磊，胡春艷. 一種基于FPGA的光纖光柵高速解調算法[J]. 光通信研究，2014（2）：39-42.

[14] 耿傳飛，俞醒. 基于L-M算法的神經網絡在環境振動分析中消除本底振動的應用[J]. 振動與沖擊，2016（13）：14-19.

[15] 劉梅，劉紅衛，楊善學，等. 基于近似Hessian矩陣的修正網格自適應直接搜索算法[J]. 南京理工大學學報，2018（2）：189-194.

[16] 薛浩，劉洋，楊宗青. 基于優化時空域頻散關系的聲波方程有限差分最小二乘逆時偏移[J]. 石油地球物理勘探，2018（4）：652-753.

[17] 朱紅蘭，倪勤，黨創寅，等. 求解無約束優化問題的分式模型信賴域算法[J]. 中國科學：數學，2018（4）：531-546.

[18] 胡夢英. 一種改進的自適應信賴域算法[J]. 中國科技信息，2016（17）：80-82.

[19] 胡天馳. 基于FPGA的矩陣算法IP核技術研究[D]. 杭州：浙江大學，2016.

[20] 王禹. 基于FPGA的矩陣求逆IP核設計技術及其實驗平臺設計[D]. 杭州：浙江大學，2016.

（責任編輯：杜能鋼）