常微分方程教學與MATLAB 的有效結合

布仁滿都拉

（赤峰學院數學與計算機科學學院，赤峰024000）

0 引言

在物理、化學、金融和醫學等很多領域中經常建立數學模型研究相關問題，其中常微分方程是經常遇到的微分方程。因此，常微分方程是理科、工科和文科的很多專業的必修課。結合常微分方程和MATLAB 解算的教學方法比傳統的理論講授教法，更能提高學生的學習興趣和知識的混合應用能力，下面用實例介紹常微分方程和MATLAB 的結合用法。

1 常微分方程的解析解和MATLAB解算

1.1 常微分方程的解析解

求方程y''-6y'+9y=4e3x通解。

解：我們先理論上算出方程組的解析解，然后給出它的MATLAB 解算。先求齊次方程的通解，特征方程為：

特征根為：

λ1,2=3

因此，齊次方程的通解為：

y=C1e3x+C2xe3x

由于3 是二重特征根，非齊次方程有形如：

y*=Ax2e3x

的特解。將它代入非齊次方程，比較x 的同次冪系數，得A=2，所以：

y*=2x2e3x

所求通解為：

y=2x2e3x+C1e3x+C2xe3x

1.2 MATLAB解算

下面用MATLAB 符號法求微分方程的解。

鍵入：

y=dsolve('D2y-6*Dy+9*y=4*exp(3*x)'，'x')

回車得出：

y=2*x^2*exp(3*x)+C5*exp(3*x)+C6*x*exp(3*x)

2 常微分方程組的解析解和MATLAB解算

2.1 常微分方程組的解析解

求解方程組

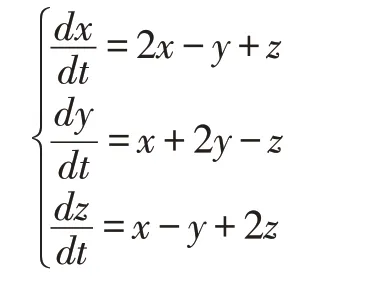
解：我們先理論上算出方程組的解析解，然后給出它的MATLAB 解算。

系數矩陣為：

特征方程為：

特征根為：λ1=3，λ1=2，λ1=1。

先求λ1=3 對應的特征向量：

a，b，c 滿足方程組：

即：

可得a=c，b=0，取一組非零解，例如令c=1，就有a=1，即：

下面求λ2=2 對應的特征向量：

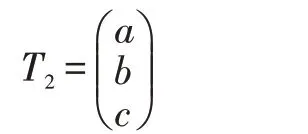
a，b，c 滿足方程組：

即：

可得a=c，b=c，取一組非零解，例如令c=1，就有a=1，b=1，即：

最后求λ3=1對應的特征向量：

a，b，c 滿足方程組：

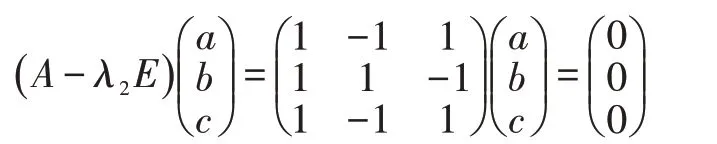
即：

可得a=0，b=c，取一組非零解，例如令c=1，就有b=1，即：

故方程組的通解是：

2.2 MATLAB解算

下面用MATLAB 符號求上述方程組的解析解：

鍵入：

回車得出：

3 常微分方程初值問題數值解及MATLAB解算

3.1 常微分方程初值問題數值解

在很多問題中遇到的常微分方程的解析解是很難算出來的，這時，我們可以用數值方法求近似解。

求解2y'+4xy=1，y(0)=0。

解：先用分離變量法和常數變易試算齊次方程的通解：

2y'+4xy=0

分離變量，得：

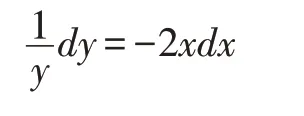
兩端積分，得：

解出y，得：

y=Ce-x2

由常數變易法，令：

y=C(x)e-x2

為非齊次方程的解，代入后得：

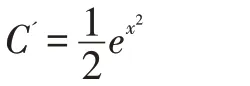
由于ex2的原函數不是初等函數，積分：

的計算無法進行。

3.2 MATLAB解算

下面用MATLAB 求該微分方程的數值解。

先建立如下M-函數文件

function y1=CDE(x，y)

y1=0.5-2*x*y;

在指令窗口中鍵入：

[x，y]=ode23(@CDE，[0 3]，[0])

回車得出：

鍵入：

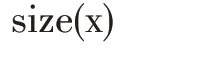
回車得出：

因此，在區間[0,3]上把x 分成了21 節點，對應地得出y 的21 個取值，即得到了微分方程的數值解。

進一步，鍵入：

plot(x，y)

回車畫出數值解的圖形，見圖1。

圖1 數值解的圖形