修正的阿倫方差對調相閃爍噪聲的抑制

北京東方計量測試研究所，北京 100086

頻率穩定度是描述原子鐘穩定性的重要指標，原子鐘頻率穩定度的算法同時也影響著原子鐘性能的評估。但是，無論在何種測量環境下，噪聲對頻率穩定度測量的影響都無法完全消除，只能采取有效措施進行抑制。一般情況下，若想更有效地消除噪聲，需要更長的測量時間；但在同等測量時間內，怎樣更有效地降低噪聲對測量的影響則成為時間傳遞的關鍵。時間傳遞的本質就是傳遞過程中噪聲本身的測量。

原子鐘的溯源問題可以利用衛星遠程共視時間比對法解決，通過共視時間比對數據可以得到原子鐘的各項性能指標，包括頻率穩定度。在對頻率穩定度進行評估時，普遍采用阿倫方差。但是，與阿倫方差相比，修正的阿倫方差有其本身算法的優勢，可以有效地抑制噪聲尤其是調相閃爍噪聲對測量的影響。本文通過衛星共視時間比對法，利用實驗室主動型氫原子鐘與原子時標國家計量基準進行時間比對。通過兩地鐘的時間差數據對頻率穩定度進行評估，并分析了修正阿倫方差抑制調相閃爍噪聲的機理。

1 原子鐘噪聲特性

原子鐘噪聲的數學模型定義原子鐘t時刻的時差值為x(t)，則原子鐘的時差模型可表示為[1-2]：

(1)

式中：a0為時刻偏差；a1為頻率偏差；a2為頻率漂移；ξ(t)為噪聲項。公式(1)稱為原子鐘時差的多項式模型，是通用的原子鐘時差數據的描述方法。時刻偏差一般指本地鐘與參考時鐘的秒脈沖1脈沖/s的相位差;頻率偏差指時間偏差的一階線性擬合的系數；頻率漂移率是頻率偏差隨時間單調變化的線性率；噪聲項是扣除原子鐘的系統性變化(即多項式模型)外的各類噪聲的綜合。對于其中的噪聲項，原子鐘的噪聲可用5種獨立的隨機過程表示[3-4]，即：

ξ(t)=z-2(t)+z-1(t)+z0(t)+z1(t)+z2(t)

(2)

式中：zα(t) (α=-2，-1，0，1，2)代表5種獨立的噪聲過程：調頻隨機游走噪聲(Random Walk FM，RWFM)、調頻閃變噪聲(Flicker FM，FFM)、調頻白噪聲(White FM，WFM)、調相閃爍噪聲(Flicker PM，FPM)、調相白色噪聲(White PM，WPM)。但是并不是每個原子鐘在測量過程中都一定含有上述全部5種噪聲，一般情況下，只是2～3種噪聲在起主要作用。

2 修正的阿倫方差降噪機理

由于噪聲的非平穩性質，尤其是“閃爍噪聲”的存在，使得用標準差表征頻率穩定度時，結果將隨采樣數的增加而發散[5-6]。為了克服閃變噪聲隨時間變化出現的非平穩問題，D.W.Allan博士提出采用雙采樣方法對原子鐘的頻率穩定度進行評估，即Allan方差[7]。

(3)

式中：xi為時差序列；N為時差采樣數；τ0為采樣間隔。Allan方差通常以均方根的形式表示[8]，ADEV或σy(τ0)。

與阿倫方差相比，修正的阿倫方差的均方根即MDEV的表達式如下[9-10]：

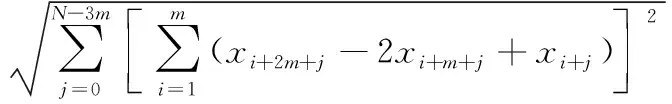
(4)

式中：xi為時差序列；N為時差采樣數；τ0為采樣間隔；m為在N采樣時差數內的采樣數。

Allan方差可以識別不同的噪聲類型[11]，對不同噪聲的表征是通過不同的取樣時間體現的[12]，即在一定的取樣時間內對應著一定的噪聲過程。在一定的取樣時間內，噪聲主要由幾種噪聲共同貢獻，但是實際上，無論采樣時間長短，5種噪聲都是共同作用在整個測量過程中的，只是噪聲系數的權重有所不同。而調相閃爍噪聲附加在信號上，引起信號的相位調制，它對短期頻率穩定度影響較大。因為附加噪聲頻譜較寬，高頻分量多樣，所以這種噪聲頻率變化很快。隨著取樣間隔的增加，這種起伏就會被平均掉。對于雙采樣的Allan方差而言，當取樣時間大于最小采樣間隔時，很多的采樣數據就沒有參與運算，取樣時間越大，未參與運算的時差數據就會越多，頻率穩定度的評估過程也就不能很好地抑制調相閃爍噪聲的影響，但MDEV卻可以很好地解決這個問題。

由式(4)可知，MDEV在計算頻率穩定度時與ADEV不同，MDEV用相鄰數據以m為長度的采樣數據的平均值作為當前計算的時差值，然后向下平移一個τ0(最小采樣間隔)的采樣數據，所有的采集數據都會參加運算。這樣的缺點是大大增加了運算量，且取樣總數也會相對減少。但對于頻率穩定度而言，MDEV可以視為對所有時差數據進行了平滑，對于高頻的噪聲能夠起到很好的濾波效果。式(4)中的m可以理解為平滑窗口的大小，隨著m的增大，平滑窗口也增大，也就是取樣數增大。但當平滑窗口過大，高頻分量的噪聲信號的平滑效果會降低，噪聲的抑制也就不再明顯。從這種角度講，MDEV也可以看成一種短期頻率穩定度評估中數據加窗平滑的降噪方法，高頻噪聲信號在時域短窗口的平滑中會被平滑掉，對于頻域而言就是被濾波掉，這就是MDEV對短期頻率穩定度評估優勢的機理。

3 試驗數據驗證與分析

試驗數據利用主動型氫原子鐘，遠程時間比對基準以原子時標國家計量基準即UTC(NIM)的時間頻率信號作為參考。通過兩地原子鐘同儒略日的CGGTTS數據處理得到氫原子鐘與UTC(NIM)的時間偏差，通過對兩地鐘時間差數據的解算可以得到平均相對頻率偏差、頻率穩定度等相關性能指標。試驗采用了共21天的共視時間比對數據，利用這21天的共視時間比對數據得到的ADEV頻率穩定度與MDEV頻率穩定度的結果如圖1、圖2所示。

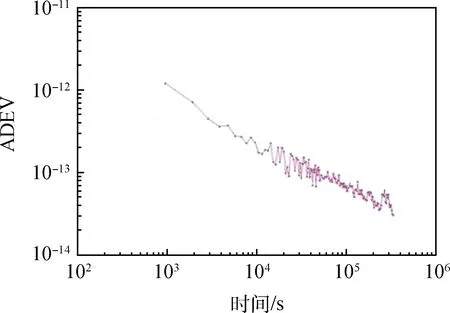
圖1 阿倫方差解算的頻率穩定度Fig.1 Frequency stability of Allan variance

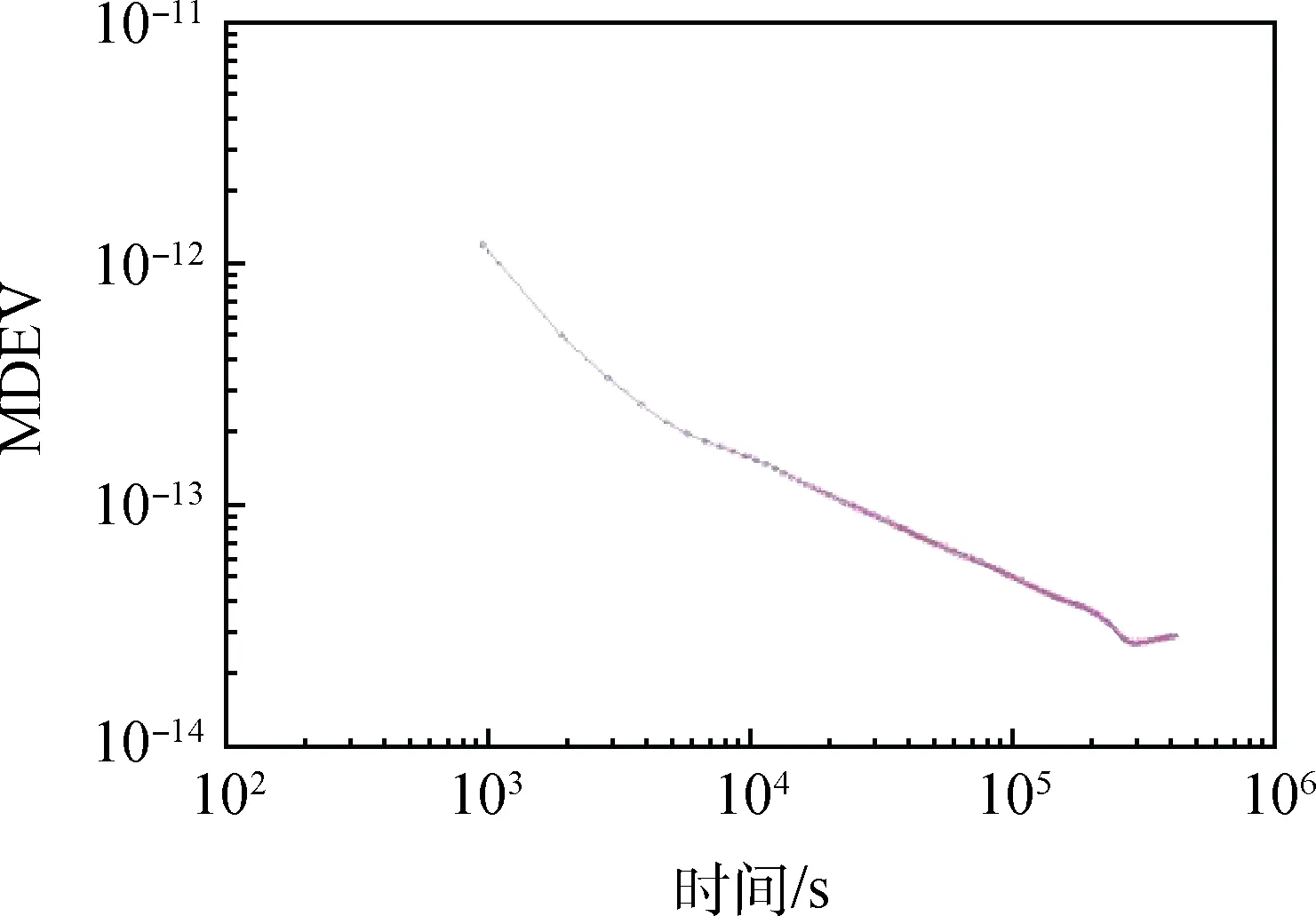
圖2 修正阿倫方差解算的頻率穩定度Fig.2 Frequency stability of modified Allan variance

比較圖1與圖2不難發現，同是頻率穩定度的計算，MDEV具有更好的數據平滑效果，在頻域范圍內也體現了MDEV濾波的效果。MDEV對于上述的5種噪聲類型的抑制情況可以通過時域噪聲模型進行驗證分析。在測試環境穩定的情況下，各個隨機項可認為是統計獨立的隨機過程，因此原子鐘的時域噪聲模型可表示為[13]：

(5)

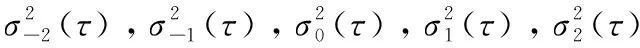
基于時域的相位噪聲理論，Allan方差噪聲模型如下[14]：

(6)

式中：τ為取樣時間；h-2、h-1、h0、h1、h2為各噪聲系數;fh為頻率上限。在已知了5個隨機噪聲項在典型時間間隔下的Allan方差值之后，通過最小二乘法擬合Allan方差的雙對數曲線，從中可以求解出各個隨機項的系數[15-16]，具體解算的系數結果如表1所示。

表1 ADEV計算的噪聲系數

由表1可知，5種噪聲類型中，調相閃爍噪聲的權重是最大的，即這種噪聲對于測量過程的貢獻是最大的，這也是Allan算法缺陷所至。現將表1計算中的5個頻率穩定度值用MDEV計算出的頻率穩定度代替，時間間隔不變，就可得到MDEV相對于ADEV在5種噪聲系數下的噪聲系數，見表2。

表2 MDEV計算的噪聲系數

從表1和表2的比較可以看出，無論是ADEV算法還是MDEV算法，在對頻率穩定度的評估方面，調相閃爍噪聲(α=1)的貢獻都是最大的。對于ADEV算法而言，h1系數的貢獻量相對于其他系數的權重更大。而利用MDEV解算得到的h1系數有明顯變小的情況。與其他噪聲系數的比例關系對比后不難發現，調相閃爍噪聲的作用仍為主導。也就是說，在頻率穩定度分析中，MDEV算法無法改變主要噪聲作用的趨勢，但會降低調相閃爍噪聲對頻率穩定度測量的影響。

4 結束語

針對原子鐘頻率穩定度的評估方法，本文提出了MDEV對于噪聲抑制的機理。試驗結果表明，在時域范圍內，短期頻率穩定度測量中的主要噪聲包括調頻白噪聲和調相閃爍噪聲。而MDEV對于調相閃爍噪聲的抑制效果明顯優于ADEV。對原子鐘進行遠程時間頻率溯源及傳遞中，MDEV更適用于頻率穩定度的評估。本文對實際的應用具有一定的價值。