基于時頻分析的靈巧干擾特征研究
李辰梓 余建宇 徐 偉 郝萬兵
(西安電子工程研究所 西安 710100)
0 引言
雷達干擾是指通過將干擾信號隨同敵方期望收到的信號一起送入敵方接收機中,當干擾信號強到足以使敵方無法從中提取到所需信息時,干擾就是有效的[1]。傳統的雷達干擾按照原理分為壓制性干擾和欺騙性干擾,壓制性干擾是指用噪聲信號或噪聲調制的強干擾信號遮蓋或淹沒目標回報信號,使雷達無法從中檢測目標的信息。欺騙性干擾即產生假的目標和信息,使雷達無法正確地檢測真實的目標,從而達到迷惑和擾亂雷達對真正目標檢測和跟蹤的目的[2]。
現代新體制雷達為了對抗干擾,雷達信號一般都采用了脈內或脈間相干的信號波形,最常見的信號形式為線性調頻信號。傳統噪聲干擾采用非相參噪聲調制產生的干擾信號,經雷達端接收進行脈沖壓縮后,噪聲信號能量大部分被濾除,使干擾效果大大減弱。并且當前雷達大都采用旁瓣消隱(SLB)和旁瓣相消(SLC)等抗干擾措施,使得傳統的干擾樣式不能夠產生干擾壓制或者假目標欺騙的效果。因此為了應對這些新的抗干擾措施而提出了靈巧干擾這一概念,它同時具有欺騙干擾和壓制性干擾的特點。由干擾機將截獲的雷達信號進行存儲并調制產生靈巧干擾信號,因此干擾信號可根據被干擾對象靈活變化與雷達發射信號相匹配,使干擾能夠獲得理想的相參積累增益,增強了可利用的干擾能量。
本文以LFM雷達信號為研究對象,對卷積調制靈巧噪聲干擾以及間歇采樣轉發干擾進行了研究仿真分析,并對不同形式干擾信號的時頻和域特征進行研究,為后續干擾及抗干擾提供先驗信息。
1 靈巧干擾
靈巧干擾的提出是為了應對如何有效干擾采用脈內或脈間相干波形的新體制相參雷達。首先對偵收的目標雷達信號利用數字射頻存儲技術(DRFM)進行完整無失真的保存,然后對存儲的雷達信號進行調制產生期望得到的靈巧干擾信號[3]。干擾信號本質上是雷達自身信號進行調制轉發,因此產生的干擾波形與雷達具有較好的相干性,信號大部分能量能通過相參雷達的檢測脈壓系統,對相參雷達產生有效的干擾[4]。
1.1 卷積調制靈巧干擾樣式
卷積噪聲干擾是將干擾機通過偵收天線將接收到的雷達信號經過濾波、放大后進行存儲,然后經過調制器將視頻噪聲信號與存儲的雷達信號作卷積,經功率放大器放大后將信號進行發射的干擾方法[5],圖1為基于DRFM的卷積調制靈巧干擾方法原理框圖。
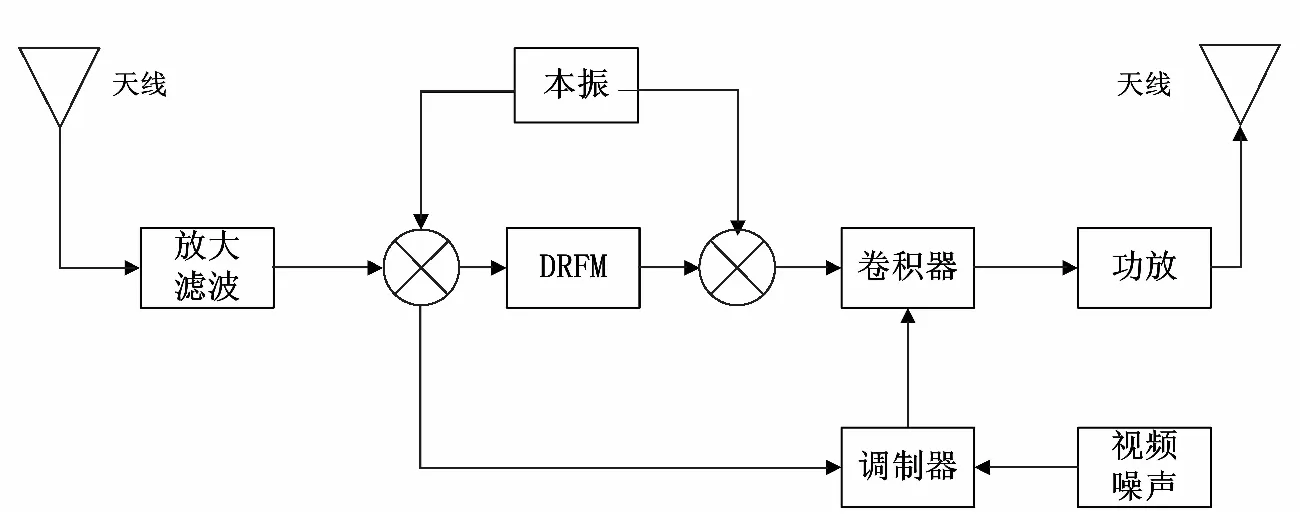
圖1 靈巧噪聲卷積調制方法原理框圖
干擾機偵察接收到的雷達信號為s(t),干擾機選取的視頻噪聲信號為n(t),干擾系統調制產生的卷積干擾信號為y(t)=s(t)*n(t)。噪聲卷積干擾使用視頻噪聲與雷達本身信號的卷積結果作為干擾信號,只要雷達信號在干擾機的瞬時帶寬內變化,干擾信號頻率也會隨之變化。也就是說干擾機不需要測頻和頻率引導,就能自動瞄準信號頻率從而具有很好的相參性,因此這種干擾方法也能對頻率捷變雷達進行干擾。干擾信號發射進入雷達接收機進行脈壓處理為:
Y(t)=y(t)*s*(t)=s(t)*n(t)*s*(t)
(1)
設s(t),n(t),Y(t)的頻譜分別為S(f),N(f),Y(f),可得:
Y(f)=N(f)·|S(f)|2
(2)
進行變化可得到:
Y(t)=n(t)*F-1[|S(f)|2]
(3)
式(3)中,F-1表示逆傅里葉變換,F-1[ |S(f)|2]稱作點擴展函數[6]。任何函數與點擴展函數卷積都可以獲得脈壓處理的增益,進一步印證了靈巧干擾對相參雷達干擾的有效性。
1.2 間歇采樣循環轉發靈巧干擾樣式
間歇采樣轉發干擾目前國內外已經有大量的研究與應用,按照不同的脈沖間歇采樣參數和轉發方式,可以在真實目標附近產生假目標群,能有效地掩蓋真實目標,在工程上對現有收發隔離式干擾機較易實現。本文研究中采用間歇采樣循環疊加轉發干擾的方式,其原理框圖如圖2所示。
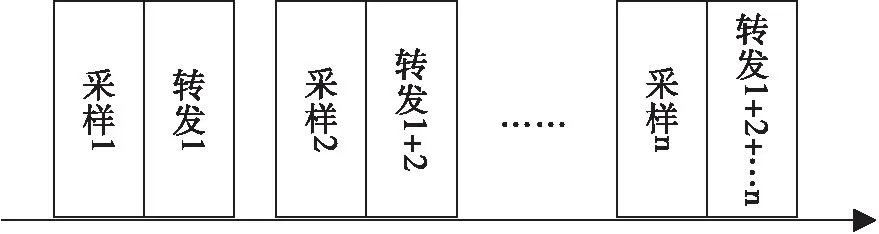
圖2 間歇采樣循環轉發干擾原理圖
可以看出間歇采樣循環轉發靈巧干擾樣式產生的干擾信號完全是對雷達信號進行復制和循環轉發,與卷積調制樣式最大的區別在于不需要額外的選用視頻噪聲來對雷達信號處理。所以本文選取卷積調制干擾和間歇采樣循環轉發干擾這兩種典型的靈巧干擾樣式進行仿真建模,對兩類靈巧干擾信號的時頻特性以及干擾效果進行研究分析,有利于從中研究對抗靈巧干擾的方法以及如何提高靈巧干擾的效果。
2 時頻分析
時間t和頻率f是信號分析和處理中兩個很重要的變量,但時間域分析信號無法看出特定時刻信號的頻率值,通過傅里葉變換在頻率域也無法得到特定頻率分量在時間上的準確分布。這時便要使用時間和頻率的聯合函數變換來分析信號,即時頻域分析。時頻變換主要分為兩類,即線性時頻變換和非線性時頻變換。典型的線性時頻變換有短時傅里葉變換,典型的非線性時頻變換有Wigner-Ville分布。
Wigner-Ville時頻分布是首先由Wigner提出用于量子力學領域,后由Ville引入信號分析而稱之為WVD。該分布為其他時頻分布的研究提供思路,信號分析和處理中,已成為了非常有用的工具,Wigner-Ville分布的表達式如公式(4):
(4)
Wigner-Ville分布可以看作是一種用信號自身作為窗函數的特殊的STFT形式,這種窗函數實際上對信號具有某種程度的自適應性使得它的信號能量聚集性很好,但是在同時多信號的情況下Wigner-Ville分布會出現較為嚴重的交叉干擾項,使正確截獲、分析信號變得非常困難。因此論文采用 WVD 的平滑形式,即Choi-Williams 分布(CWD)作為離線的信號的描述方法。CWD屬于Cohen類分布,它是由Wigner-Ville分布通過與不同的核函數卷積產生[7],其表達式如公式(5)所示:
(5)
Choi-Williams分布使用的核函數偏重于抑制遠離原點的交叉項,這種特征對于大多數脈內調制信號來說是適用的,因此選來對于由雷達脈內調制的干擾信號進行時頻域分析。
3 靈巧類干擾樣式的仿真及時頻分析
本次仿真條件設置如下,雷達信號S(t)選用線性調頻信號,數學表達式如公式(6)所示:
(6)
其中信號時寬T為60μs,帶寬B設置為20MHz,中心頻率f0為50MHz,對雷達信號的采樣率設置為100MHz。仿真得到雷達信號S(t)的時域圖像、頻域圖像、經過雷達匹配濾波后產產生的脈壓圖像和時頻域分析圖像如圖3、圖4所示。

圖3 LFM信號時域圖
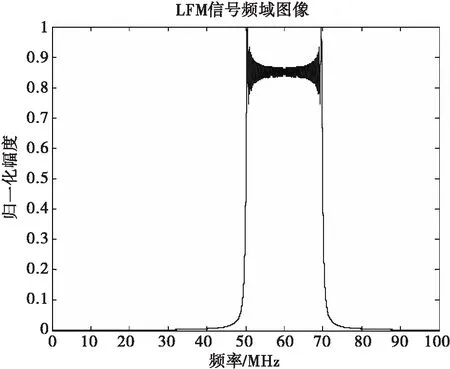
圖4 LFM信號頻域圖

圖5 LFM信號脈壓圖
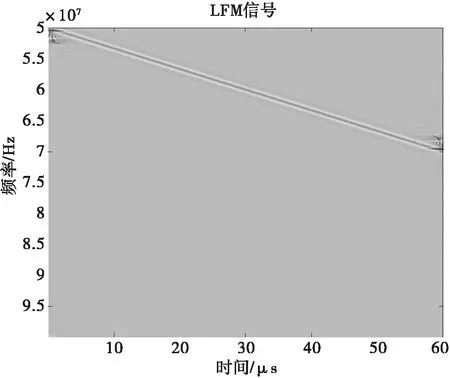
圖6 LFM信號CWD圖
由圖6中CWD圖可以清楚地看到LFM信號時間-頻率的對應關系,頻率在50MHz~70MHz隨時間線性變化,能準確的捕捉信號的時頻特征。
3.1 卷積噪聲靈巧干擾仿真
3.1.1 視頻噪聲為高斯白噪聲
選用均值為0,方差為1,時寬為10μs的高斯白噪聲信號作為視頻噪聲信號。
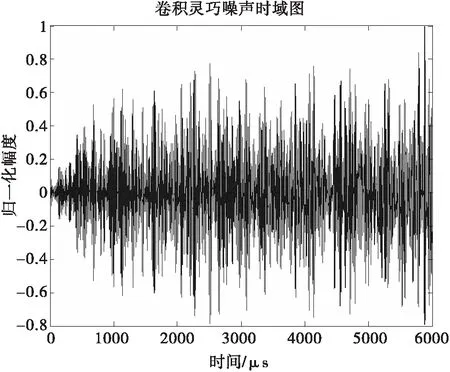
圖7 靈巧噪聲時域圖
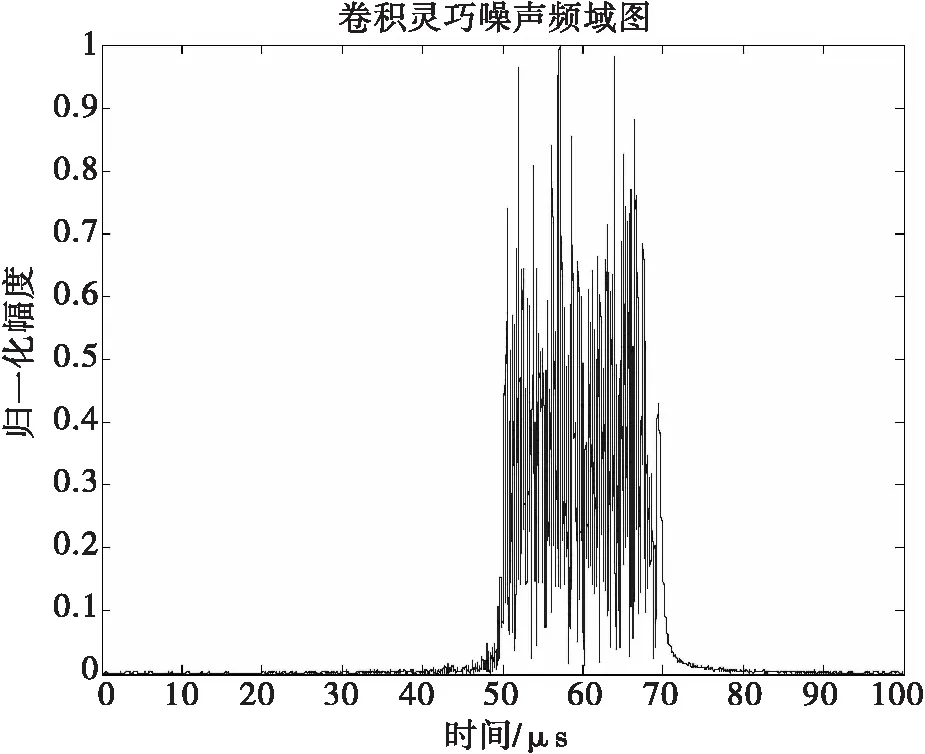
圖8 靈巧噪聲頻域圖
由圖8可以清楚地看出靈巧噪聲信號的的中心頻率、帶寬很好地對準了線性調頻信號的中心頻率和帶寬(50MHz~70MHz),能夠造成良好的干擾效果。圖9可以看到靈巧噪聲信號通過雷達接收機的匹配濾波后出現了遮蓋波形,能夠遮蓋住本身的雷達信號,產生了壓制干擾的效果。并且經過多次仿真可以得出,選用的高斯白噪聲時寬越寬,匹配濾波后壓制干擾效果也會更好。
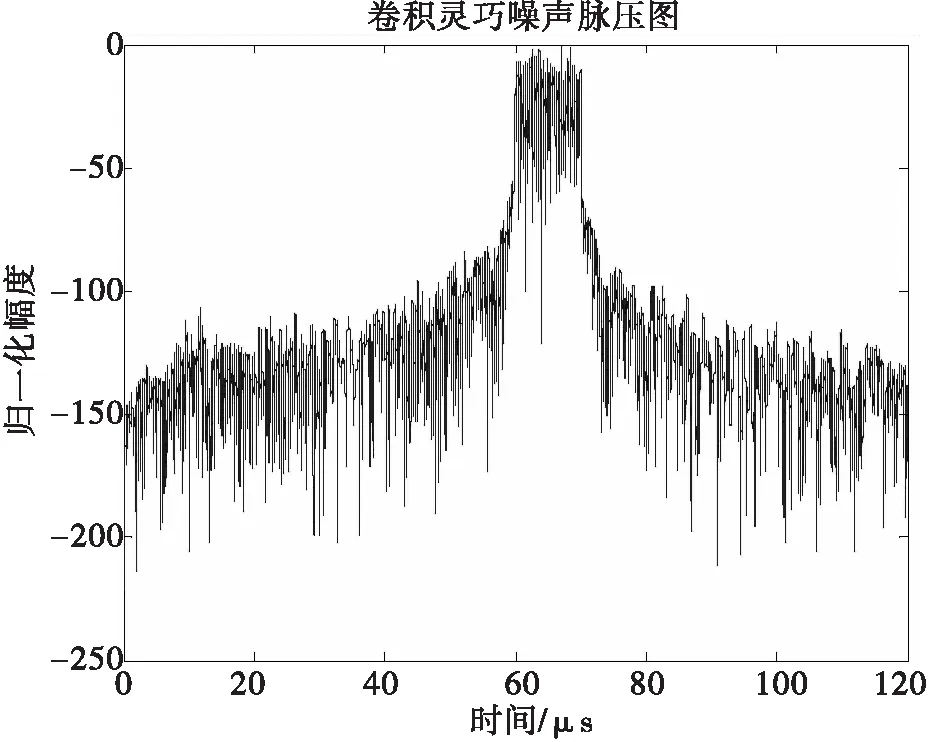
圖9 靈巧噪聲脈壓圖
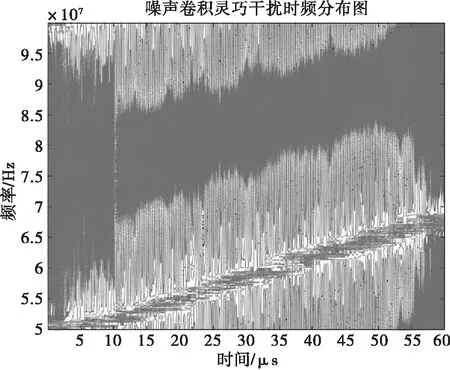
圖10 靈巧噪聲CWD圖
通過Choi-Williams分布對干擾信號視頻分析得到圖10,高斯白噪聲產生具有高斯分布特性,但通過卷積干擾能夠自動瞄準LFM信號頻率,所以產生的靈巧干擾信號在時頻域準確地遮住了LFM信號,能夠很好地產生壓制干擾效果。
3.1.2 視頻噪聲為矩形連續脈沖
n(t)選用為周期方波信號,參數設置為脈寬2μs,周期4μs,持續時間為40μs,幅度為1。
矩形脈沖與LFM信號卷積,等價于將LFM信號分別移位至每個矩形脈沖的位置,因此,卷積結果相當于不同延時的線性調頻信號的疊加。并且由圖13可以看出干擾結果產生了多個壓縮峰,其間隔均小于線性調頻信號的脈寬,達到了要求產生脈內高密度假目標的目的。由圖14時頻分析圖可以看出矩形方波卷積靈巧干擾產生的假目標在時間上分布均勻,頻率域完整地保留了LFM信號的全部信息,且產生的假目標幅度大致相同。
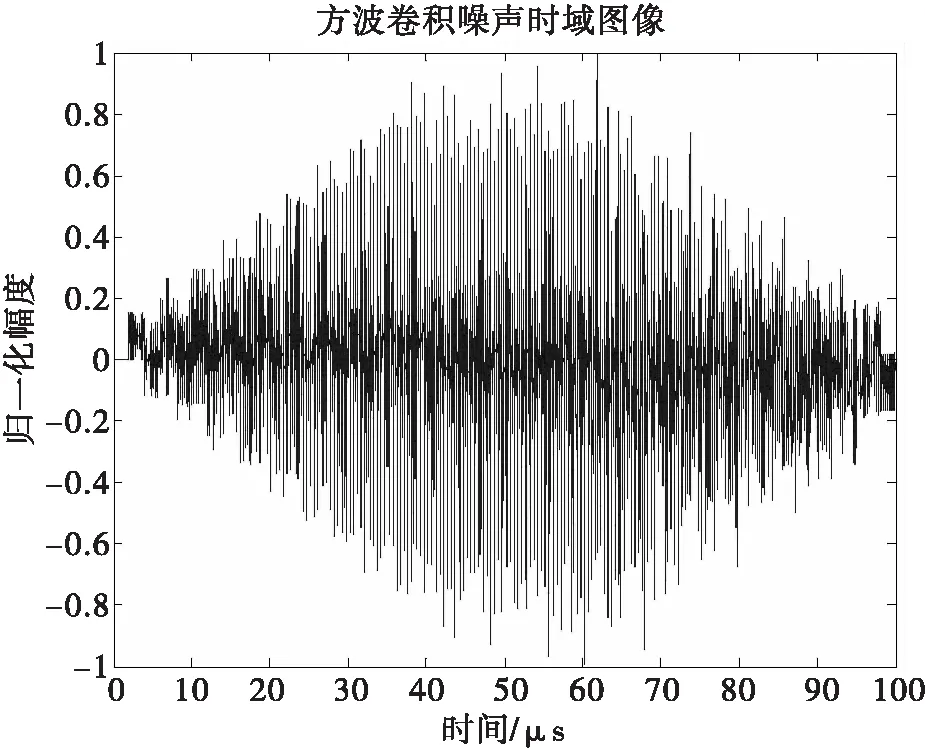
圖11 靈巧噪聲時域圖
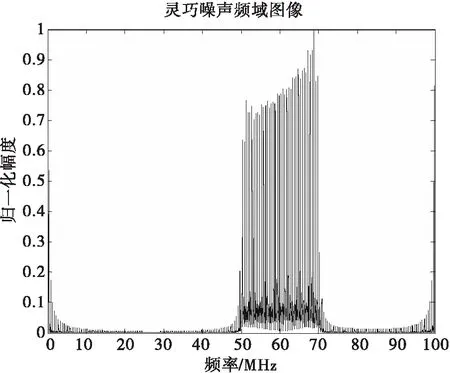
圖12 靈巧噪聲頻域圖
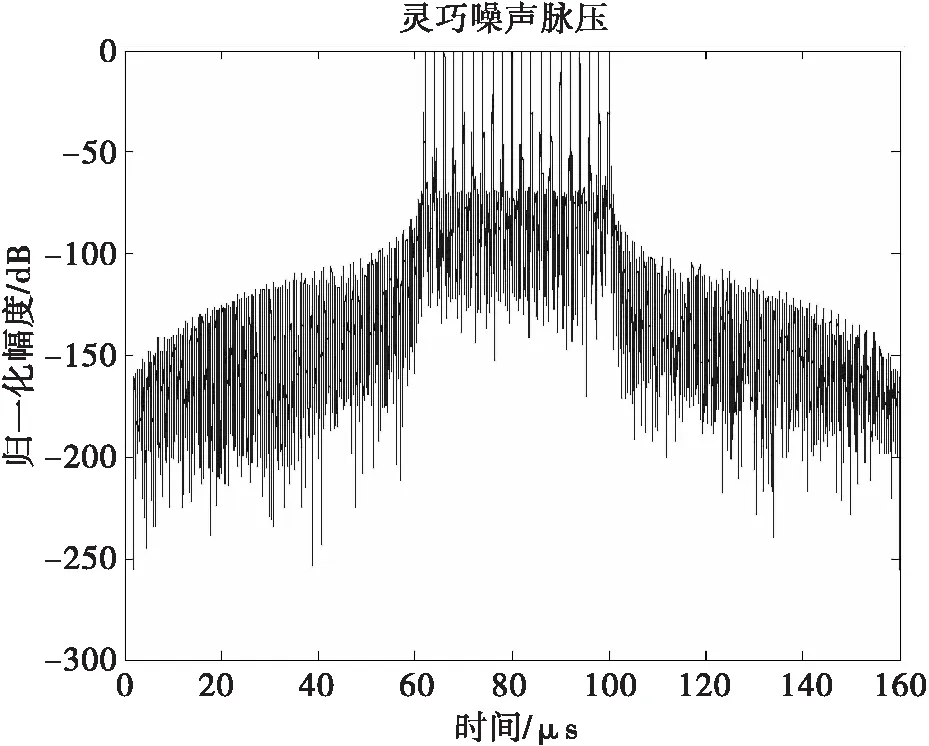
圖13 靈巧噪聲脈壓圖
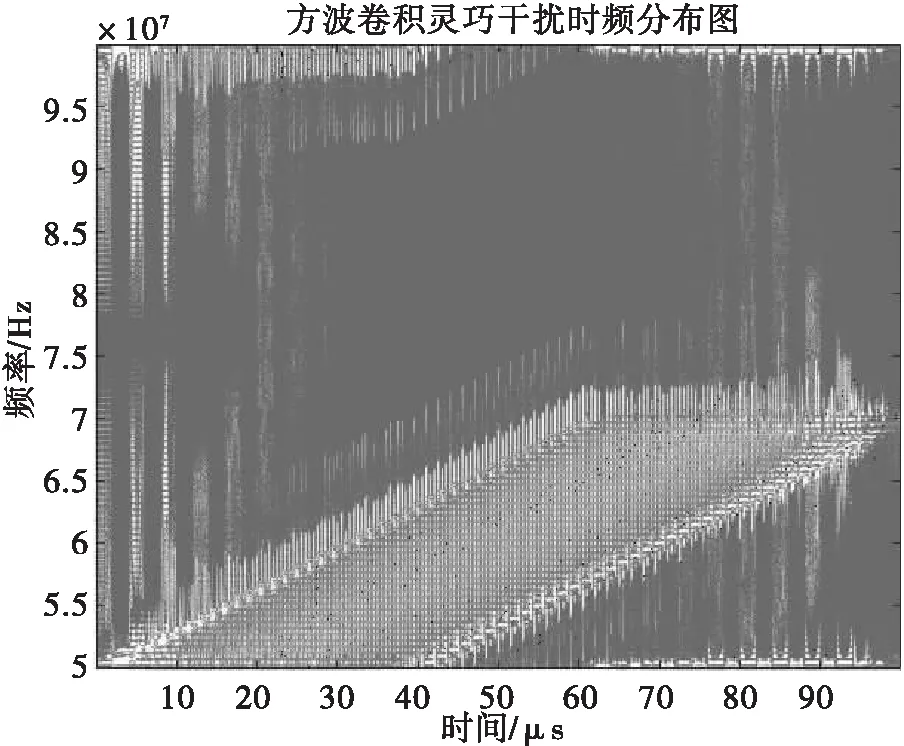
圖14 靈巧噪聲CWD圖
這些密集的假目標將會淹沒真實目標或使被干擾雷達的處理能力飽和,從而使雷達不能準確地捕捉目標。根據多次仿真發現,改變矩形脈沖串中脈沖的個數,會影響假目標的數量,脈沖數目越多,產生的假目標就越多,密度就越大,干擾效果越好。但此種干擾產生的假目標間隔均勻,幅度基本一致,也可以用此特性來進行抗干擾處理。
3.2 間歇采樣循環轉發干擾
仿真中對LFM雷達信號S(t)進行間歇采樣循環轉發,一個采樣轉發周期為5μs,每次采樣雷達信號之后,在一個周期剩下的時間內,轉發的信號為之前存儲的信號與當前采樣信號的疊加,仿真結果如圖15所示。
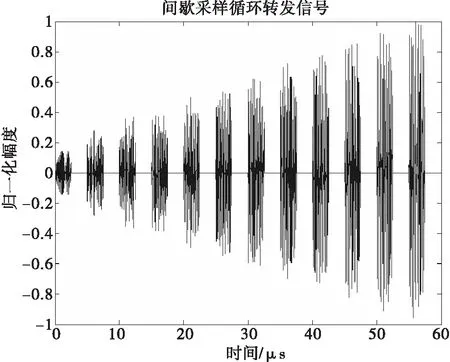
圖15 循環轉發干擾時域圖
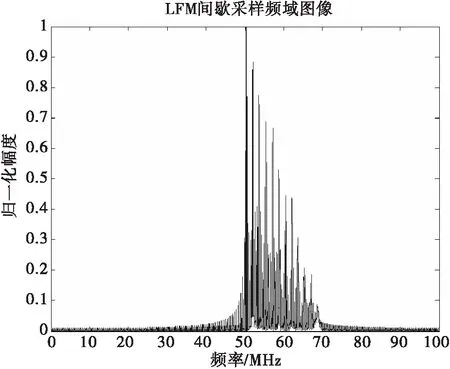
圖16 循環轉發干擾頻域圖
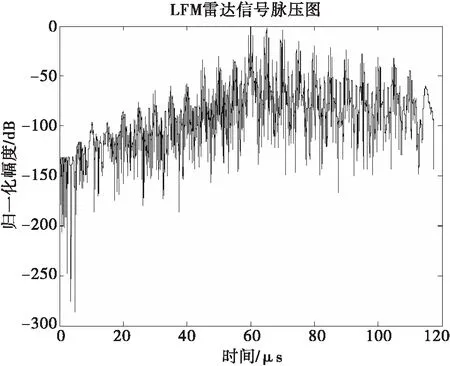
圖17 循環轉發干擾脈壓圖
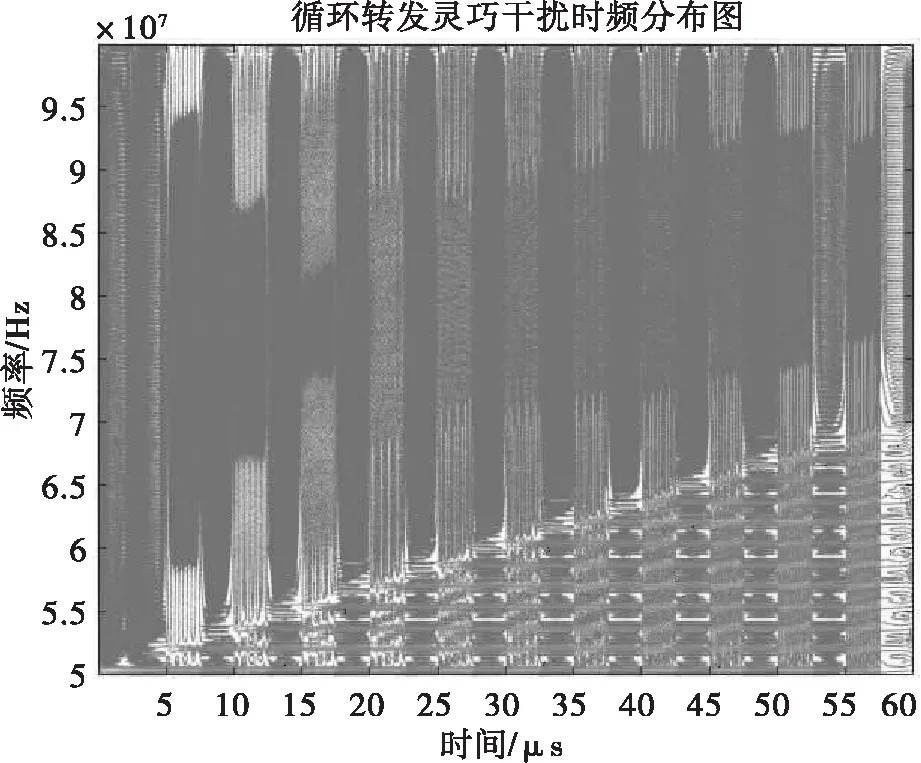
圖18 循環轉發干擾CWD圖
從干擾信號頻域圖16和脈壓圖17可以看出,干擾信號本身是雷達自身信號的轉發,干擾信號頻率對準LFM信號,因此干擾具有較高的相參性,能夠產生較好的干擾效果。從圖18時頻分析CWD圖可以看清楚地看出,隨著采樣時間的推移,當前的干擾信號是由當前采樣的LFM信號與之前所有采樣LFM信號的疊加,包含之前采樣得到所有信號的全部信息。并且通過多次仿真發現通過改變一個采樣轉發周期的速率,可以改變產生假目標的密集度,采樣轉發速率越高,形成的假目標數目就越密集。但是通過時頻分析圖也可以看出間歇采樣循環轉發干擾信號在整個脈沖持續時間內是非連續的,因此該特性可以被用來實現間歇采樣轉發干擾信號的識別和抑制。
4 結束語
靈巧干擾兼有欺騙干擾和壓制性干擾的特點,并且實現具有很大的靈活性,在未來電子對抗中會發揮出越來越重要的作用。本文對卷積類靈巧干擾和間歇采樣循環轉發干擾建模,仿真研究改變干擾參數設置對干擾效果的影響,并且采用時頻分析Choi-Williams分布來提取出干擾信號的時頻域特征,有利于進一步優化靈巧干擾的干擾效果,使其在電子對抗中有更廣闊的運用。

