車體振動對接觸網檢測的影響分析及補償方法研究

張冬凱， 高仕斌， 于 龍， 占 棟， 康高強

(西南交通大學 電氣工程學院， 四川 成都 610031)

目前我國軌道交通主要采用受電弓和接觸網滑動接觸的方式對電力機車供電，其中接觸網是牽引供電系統的關鍵組成部分之一，它作為牽引供電系統中的無備用設備，一旦發生事故，勢必造成列車停運甚至更嚴重的后果[1]。隨著我國軌道交通運營里程逐年增加及列車運行速度的不斷提高，接觸網維護壓力不斷增大，面對巨大的接觸網維護壓力，接觸網幾何參數檢測作為接觸網維護的重要依據，檢測精度的提高越發重要。

文獻[2]通過建立檢測車車體振動數學模型，依據接觸式傳感器測量的弓網相對位移及車體位移數據，采用最小二乘擬合，得到接觸網拉出值振動補償函數，依此對接觸網拉出值檢測數據進行補償。文獻[3]通過在轉向架上安裝位移傳感器和加速度傳感器，分別測量車體相對于轉向架和轉向架相對于軌道的水平和垂直位移及側滾角，并將測量數據應用于補償算法進行車體振動補償。文獻[4]依據接觸線模型建立卡爾曼濾波導高修正模型，利用該模型對接觸網導高檢測數據進行修正以補償車體振動。以上關于接觸網動態檢測車體振動補償的研究對于提高檢測精度均取得了一定效果，但基于接觸式傳感器檢測接觸網幾何參數誤差較大，基于多傳感器分別測量轉向架及車體偏移和偏角的檢測方法，系統構建復雜，容易產生累計誤差，基于數學模型的修正方法難以反映檢測車運行時的真實振動情況，因此以上車體振動補償方法的研究不夠嚴密，無法有效地解決車體振動帶來的檢測誤差。

近年來，機器視覺檢測技術在軌道交通檢測領域得到廣泛應用。本文基于機器視覺技術通過激光攝像傳感器跟蹤車體相對軌道的姿態變化情況，推導補償計算公式，以提高接觸軌導高、拉出值檢測精度。

1 檢測原理

1.1 原理簡介

接觸網檢測及補償裝置均采用激光攝像傳感器，傳感器由1臺攝像機和1個激光器組成。檢測車結構示意見圖1，接觸網檢測裝置采用1臺激光攝像傳感器安裝于車頂中央，激光斷面垂直照射接觸網，攝像機捕捉激光斷面圖像并提取特征點圖像坐標，計算特征點在世界坐標系下的對應坐標值以計算接觸網導高和拉出值；補償裝置采用2臺激光攝像傳感器對稱安裝于補償梁兩端，補償梁安裝在車體下方與接觸網檢測裝置位于同一斷面，2臺傳感器分別照射鋼軌內側面，跟蹤車體相對鋼軌軌平面的姿態變化情況，用以補償車體振動造成的接觸網檢測誤差。

1.2 檢測裝置標定模型

基于機器視覺的檢測方法，需對攝像機進行標定，建立攝像機圖像坐標系與世界坐標系的對應關系。本文依據攝像機非線性模型[5]，通過將已知的圖像坐標點和對應的世界坐標點帶入攝像機標定模型求解攝像機模型參數，以建立二者的對應關系。

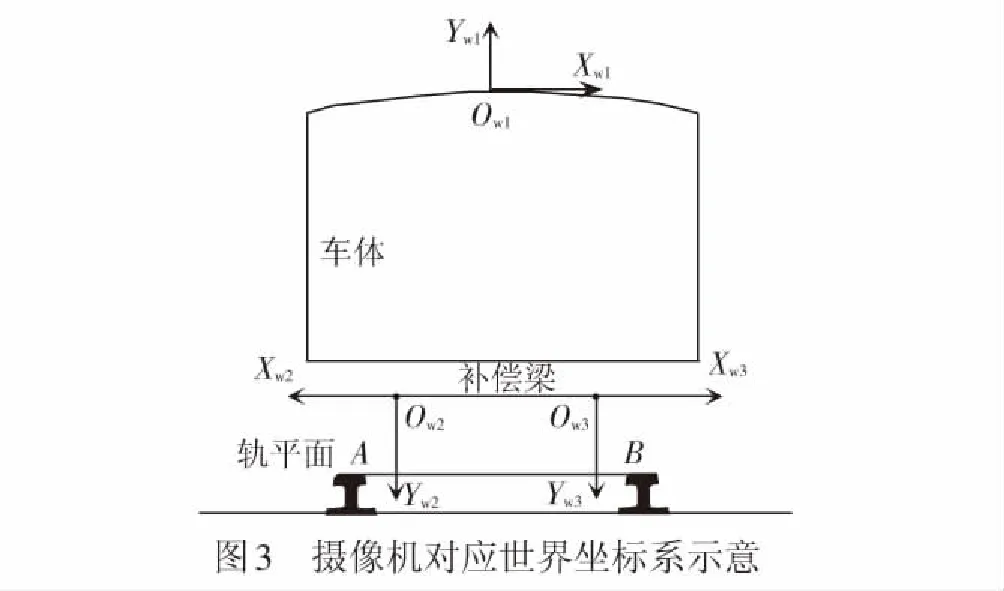
如圖2，建立世界坐標系OwXwYwZw，攝像機坐標系ocxcyczc；攝像機圖像像素坐標系OEXEYE，XE為水平像素陣列方向，YE為垂直像素陣列方向；同理，以圖像平面π中心點為坐標原點建立圖像物理坐標系OoXoYo。3臺檢測攝像機的世界坐標示意見圖3，坐標系Ow1Xw1Yw1Zw1為接觸網檢測攝像機世界坐標系，Ow1Xw1Yw1垂直于軌平面，Ow1Zw1沿軌行方向；同理，坐標系Ow2Xw2Yw2Zw2和Ow3Xw3Yw3Zw3為左右對稱的2臺補償用檢測攝像機世界坐標系。

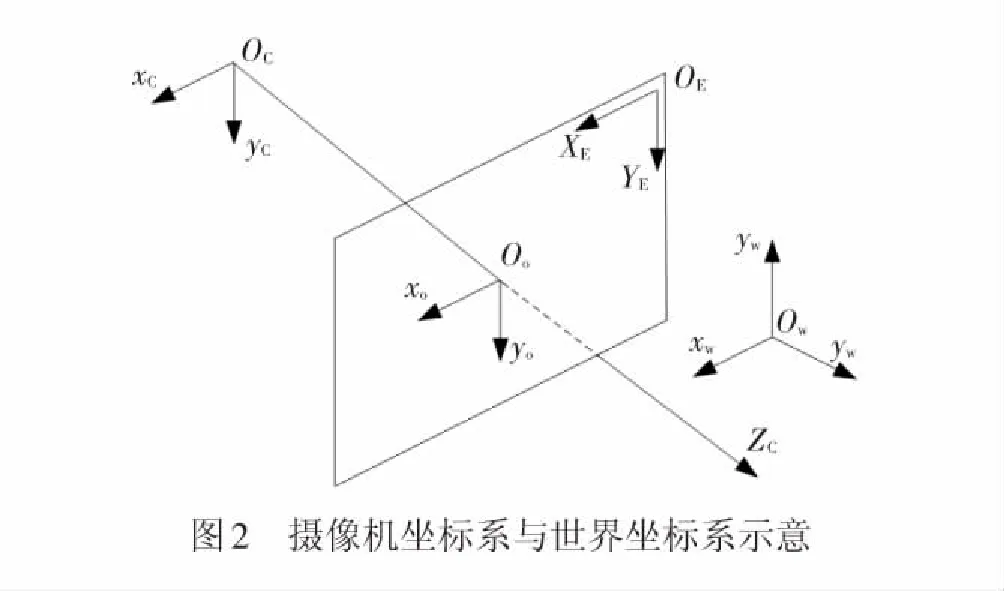
根據攝像機投射定理，即建立坐標系ocxcyczc與OEXEYE之間的投影關系為

( 1 )

式中：α、β分別為XE軸和YE軸的比例因子；γ為橫向與縱向不垂直度因子；(u,v)為圖像平面中心點O的圖像像素坐標。

攝像機參數(α,β,γ,u,v)只與攝像機內部的攝像機坐標系和圖像坐標系相關，故稱為攝像機內部參數。攝像機坐標系OcXcYcZc可通過旋轉和平移變換到世界坐標系OwXwYwZw，二者之間的關系為

( 2 )

式中：R、M分別為旋轉矩陣和平移矩陣，兩矩陣共同作用表征了內部攝像機坐標與外部世界坐標的對應關系；參數(r1～r9,m1～m3)稱為攝像機的外部參數。

世界坐標系為三維坐標系，而攝像機圖像坐標系為二維坐標系，故標定時設z=0，并將式( 2 )帶入式( 1 )，可得

( 3 )

由于攝像機鏡頭存在畸變，設畸變后圖像像素坐標為(ud,vd)，畸變前后關系為

( 4 )

式中:Δu、Δv分別為XE、YE方向的畸變量。

畸變后圖像物理坐標系坐標(uo,vo)與圖像像素坐標(ud,vd)之間的關系為

( 5 )

根據文獻[7]中的攝像機畸變模型，結合式( 4 )和式( 5 )，可得畸變量表達式為

( 6 )

( 7 )

通過棋盤格標定法進行標定，采用非線性最小二乘法求解式( 7 )中攝像機模型參數(a1,a2,…,a8,k1,k2,s1,s2)，即可建立世界坐標和圖像像素坐標之間的對應關系。

2 車體振動及對檢測系統的影響分析

2.1 車體振動分析

由于軌道不平順以及車輛自身結構等因素的激擾作用，車輛在運行時不可避免的會發生隨機振動。一般講，當車輛系統發生振動時，車體會出現伸縮、沉浮、點頭、橫擺、側滾和搖頭6種形式的隨機振動。為方便對車體振動問題的研究，假設輪軌嚴密咬合，振動過程中上下心盤之間始終保持平面接觸，并引入一系當量彈簧等效車輛轉向架的多系彈簧組[6-7]。

車輛在縱平面內的隨機振動模型見圖4，其中y為車體質心的垂向振動偏移；l為車體質心到當量彈簧的縱向距離；Ksy為當量彈簧的垂向懸掛剛度；Jcx為車體繞x軸的轉動慣量；M為車體質量；φ為車體點頭角。由車體上所受靜力和慣性力之和為零可得

( 8 )

式中：fst為一系當量彈簧的靜撓度；2Ksy(y+fst-lφ)和2Ksy(y+fst+lφ)分別為前后轉向架的垂向懸掛反力。式( 8 )經整理后可得

( 9 )

(10)

由車體沉浮振動和點頭振動方程式( 9 )和式(10)可知，車體沉浮振動和點頭振動是相互獨立的。

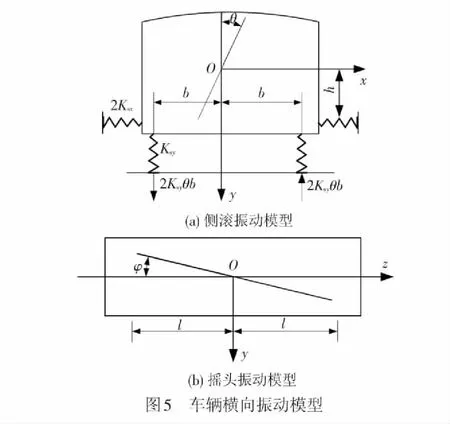
車體橫向振動模型見圖5。其中，Ksx為當量彈簧的橫向剛度；2b為當量彈簧橫向跨距；h為車體中心距懸掛上支撐面垂直距離；θ為側滾角；φ為搖頭角。

根據車體上各力的平衡條件可得

(11)

式中：x-θh+φl和x-θh-φl為前后轉向架橫向變形量。

經整理得

(12)

(13)

由車體橫擺、側滾和搖頭振動方程式(12)和式(13)可知，搖頭振動是獨立的，而車體橫擺振動和側滾振動是相互耦合的，這種耦合的振動成為滾擺振動。滾擺振動根據所擾軸心位置的不同通常分為上心滾擺和下心滾擺。

車輛的伸縮振動為沿車輛行進方向即z軸方向的振動，其與沉浮、點頭、滾擺和搖頭振動相互獨立。

2.2 車體振動對檢測系統的影響

由1.1節中所述的檢測原理可知，檢測斷面為垂直于線路方向的橫向斷面，車體伸縮振動方向與檢測斷面正交，對檢測系統不產生影響，而橫擺和沉浮振動會使車體產生水平位移Δx′和垂直位移Δy′，從而影響檢測系統精度。

(14)

(15)

當發生側滾振動時相機世界坐標系變化見圖6(c)。其中θ為側滾角；A為接觸線。則由于側滾振動產生的檢測誤差為

(16)

文獻[13]對模擬試驗車點頭角、側滾角和搖頭角的研究試驗，點頭角最大3.1°，側滾角最大4.7°；文獻[14]中論述搖頭角為3°時輪軌接觸點會發生明顯跳躍。在實測中非極限情況下側滾角一般小于2°，點頭角和搖頭角則更小。高鐵接觸網檢測中，激光攝像傳感器安裝高度約為5 000 mm，接觸網導高約為5 300 mm，最大拉出值約為300 mm，現按照上述極限情況計算誤差，即點頭角3.1°，搖頭角3°，側滾角4.7°，Ow1B為300 mm，Ow1C為300 mm，帶入上述計算式(14)～式(16)，可估計側滾、搖頭和點頭振動對檢測數據可能造成的最大誤差，見表1。

表1 振動誤差分析

由表1可知，點頭和搖頭振動對檢測系統產生的影響較小，而側滾振動對檢測系統影響較大，故可不考慮點頭和搖頭對檢測系統的影響，又因為橫擺和側滾是相互耦合的，統稱為滾擺振動，故實際車體振動補償只需要對車體的滾擺和沉浮振動進行補償，忽略點頭和搖頭振動影響。

3 振動補償方法

接觸網檢測車體振動補償裝置見圖7(a)，由補償梁和2組激光攝像傳感器組成。激光攝像傳感器2#和3#安裝于補償梁上，補償梁安裝于車體下方與接觸網檢測裝置位于同一斷面，補償梁與車體剛性連接，其與車體看作剛體，動態下車體及補償梁產生的彈性形變忽略不計。傳感器2#和3#跟蹤左右鋼軌特征點，以車體靜態姿態為基準，計算動態過程中車體姿態的變化所產生的水平、垂向偏移和偏移角，對振動誤差進行補償。

如圖7(b)，建立以檢測梁中心為原點的世界坐標系OwXwYw：OwXw為水平方向，OwYw為垂直方向。靜態時2#和3#攝像機世界坐標系O2X2Y2和O3X3Y3，其中Ow為O2O3中點，即補償梁中心，接觸網檢測裝置世界坐標系為O1X1Y1，1#攝像機到檢測梁中心的垂直距離為OwO3，根據幾何關系，將3個傳感器各自的世界坐標系通過平移統一到世界坐標系OwXwYw下為

(17)

靜態時，測得左右股鋼軌軌距點上方16 mm處的軌平面特征點A和B分別在2#和3#攝像機世界坐標系下的坐標為(x2,y2)和(x3,y3)，接觸網檢測傳感器測得接觸線特征點C在1#攝像機世界坐標系下的坐標為(x1,y1)，車體靜態傾斜角θ′為

θ′=arctan[(y2-y3)/(x3-x2)]

(18)

θ″=arctan[(yw2-yw3)/(xw3-xw2)]

(19)

接觸線上上任意特征點C在接觸網檢測攝像機世界坐標系中的坐標為(xw1,yw1)。

根據靜態基準數據和動態檢測數據，可計算出車體震動補償角θ、軌距AB為

(20)

由圖7(c)幾何關系可得，特征點C到接觸網檢測攝像機世界坐標系原點的水平和垂直距離為

(21)

根據式(21)、式(20)和圖7幾何關系，可得接觸網導高D和拉出值L振動補償后的計算式

(22)

4 試驗

4.1 鄭徐客專高速鐵路接觸網檢測試驗

選取鄭徐客專線蘭考南至民權北上行區間進行檢測試驗，檢測攝像機的檢測頻率為80幀/s，檢測車檢測運行速度為80 km/h，抽取該區段K299+447～K308+786支柱位置處接觸線拉出值數據點200個，通過比較重復性[11]和比照人工測量值對檢測數據進行驗證，其中重復性精度是檢測車以相同速度和方向對同一線路同一區段進行2次檢測，2次檢測數據的對應誤差值滿足95%以上的差值不超過測量精度限值。

表2 補償前后數據對比

表3 拉出值檢測數據和對比

表4 拉出值檢測數據和對比

表5 實測數據 mm

表6 數據均值、方差統計

4.2 杭州地鐵2號線接觸網檢測試驗

選取杭州地鐵2號線K12+255～K12+474區間進行檢測試驗，通過比照人工測量值對補償前后檢測數據進行分析，驗證補償方法有效性，試驗方式與4.1所述相同。

接觸網檢測車補償前后的剛性接觸網檢測拉出值數據及人工檢測數據對比曲線見圖11，補償前接觸網拉出值檢測數據與人工檢測數據對比的誤差曲線見圖12(a)，補償后拉出值檢測數據誤差曲線見圖12(b)。分析誤差曲線可知補償前檢測數據最大誤差25.4 mm，誤差均值11.92 mm，補償后檢測數據最大誤差-5.7 mm，誤差均值1.67 mm。實驗結果表明，補償后數據更接近于人工測量值，可信度更高，從而進一步證明車體振動補償的有效性。

5 結論

(1) 論述了基于機器視覺技術的接觸網檢測車車體振動補償檢測裝置及其檢測原理，建立了檢測攝像機的非線性標定模型。

(2) 分析了車體運行過程中的多自由度振動的相互關系及其對接觸網檢測的影響，得出了一種基于機器視覺的接觸網檢測車車體振動補償方法，對補償車體振動帶來的檢測誤差具有良好效果。

(3) 將接觸網檢測車車體振動補償裝置應用于接觸網檢測車，在鄭徐客專線以及杭州地鐵2號線進行動態試驗，試驗結果表明，車體振動補償方法效果良好。