基于聚類分析的“拍照賺錢”科學定價
張澤 張天賀 李瑤

【摘 ?要】采用聚類分析的方法,篩選任務較為集中的區域并進行分類。然后,計算吸引度矩陣與閾值,設定最大吸引準則、信譽優先分配準則為約束條件,并建立雙目標優化定價模型。最后,求解得到任務完成率為90.91%,與問題最初方案相比,成本降低10.96%,任務完成率提高45.42%;與問題二定價方案相比,成本降低5.7%,任務完成率提高7.52%。
【關鍵詞】聚類分析;拍照賺錢
引言
為提高任務完成效率,考慮將任務位置比較集中的這些聯合打包發布。因此,我們首先根據任務位置信息判斷分布較為集中的任務包括哪些,從而制定打包方案。附件一中任務的位置信息是經緯度數據,以經緯度數據為地理位置的定量分析數據。采用聚類分析的方法,對任務的位置分布進行精準的分類。
1.第一次聚類分析
首先,大致估算聚類分析的類數,因為任務總數是845個,若將任務按照位置信息分成150類,平均每類約5-6個任務,個數較為合理。因此,初次聚類時,把任務分布分成150類,利用MATLAB中K-Means命令作出聚類分析圖:
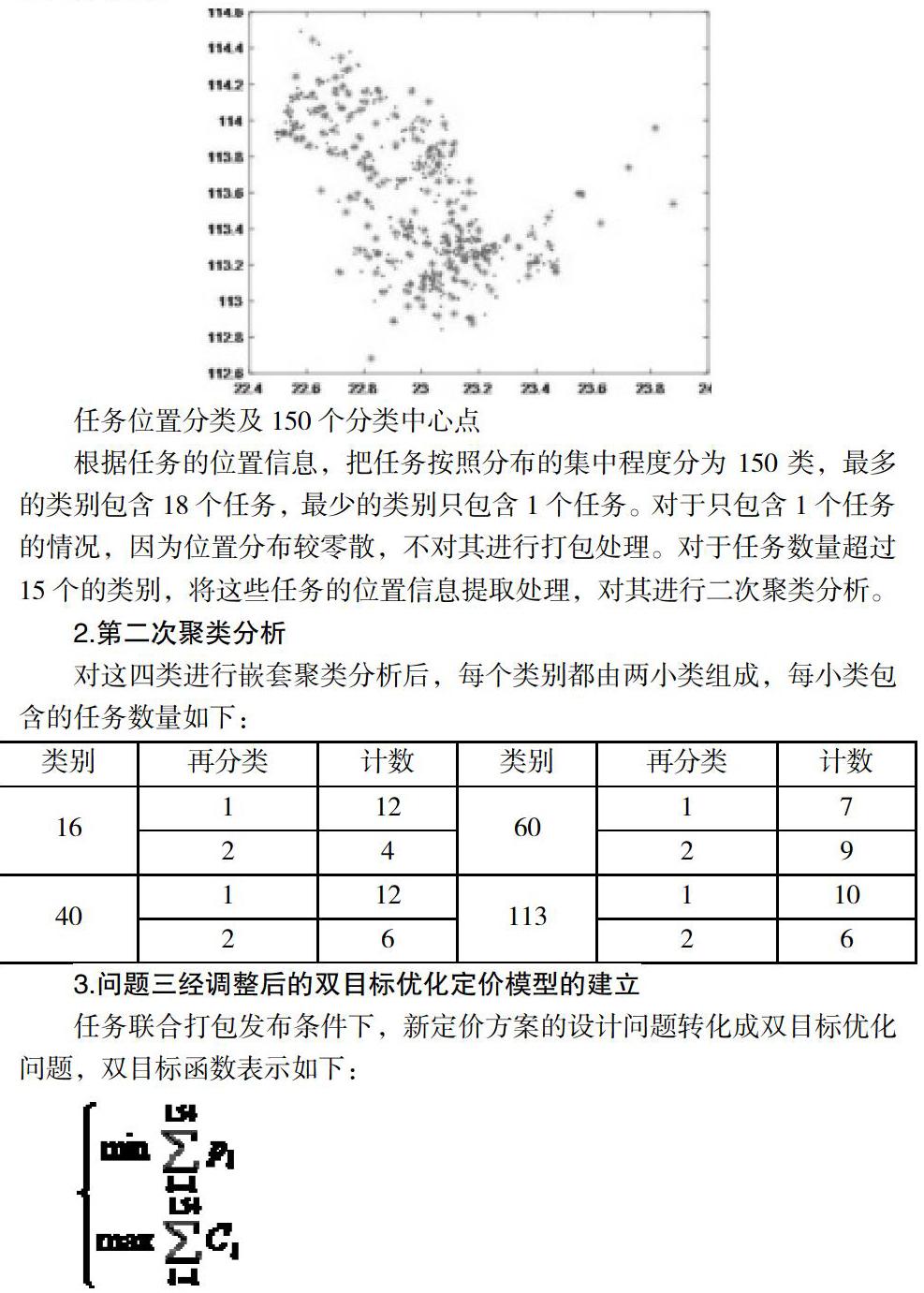
任務位置分類及150個分類中心點
根據任務的位置信息,把任務按照分布的集中程度分為150類,最多的類別包含18個任務,最少的類別只包含1個任務。對于只包含1個任務的情況,因為位置分布較零散,不對其進行打包處理。對于任務數量超過15個的類別,將這些任務的位置信息提取處理,對其進行二次聚類分析。
2.第二次聚類分析
對這四類進行嵌套聚類分析后,每個類別都由兩小類組成,每小類包含的任務數量如下:
3.問題三經調整后的雙目標優化定價模型的建立
任務聯合打包發布條件下,新定價方案的設計問題轉化成雙目標優化問題,雙目標函數表示如下:
在利用雙層嵌套聚類分析得出合理的打包方案后,任務書變為154。問題是在對任務聯合打包的基礎上優化模型進行修稿,在把多個位置較為集中的任務聯合打包發布的前提下,得到最優的定價方案。
4.雙目標優化定價模型的求解
(1)聚類打包
采用聚類算法,對任務分類,較為相似的任務分為一類成為一個任務包。部分為歸入聚類類別的個體單獨劃分為一個任務包。
(2)預先設置任務標價
采用和問題二不同的定價模式,根據聚類算法,分別得到每個任務包總單個任務的最高、平均和最低價格,進而分為三種情況,將每個包中最高、平均和最低價格作為打包任務的整體均值。
(3)吸引度矩陣
計算會員與每個任務包之間的距離,由吸引度計算公式,重新計算每個任務對于每個會員的吸引度矩陣。
(4)沖突判斷
判斷位置記錄矩陣是否存在數值相等的情況,即判斷是否存在沖突。若發生,比較會員信譽值,確定一個優先選擇,即信譽值高的會員得到本次任務預定權。
5.問題結果的分析
通過對時間和任務預定數的觀察,得到最終任務完成率的矩陣,輸出任務完成率數值和預先設定的任務定價矩陣。接下來設定幾組不同價格調整比例,得到835個任務的定價及完成率,因數據較多,此處只展示部分結果:
問題最優定價方案下,成本為51382,任務完成率為0.9091。
與原方案相比,成本降低了10.96%,任務完成率提高了45.42%。
與問題二定價方案相比,成本降低了5.7%,任務完成率提高了7.52%。
參考文獻:
[1]孫建新,石鵬翔,吳一凡.基于遺傳-RBF神經網絡的“拍照賺錢”定價方案的優化[J].數碼設計,2017,6(8):15-16.
[2]朱可,歐陽建新,劉艷,等.“拍照賺錢”任務定價的分析[J].貴州師范學院學報,2018,v.34;No.205(3):28-31.
[3]鄧明華.“拍照賺錢”問題的任務定價解題思路[J].數學建模及其應用,2018(1):33-36.
作者簡介:
張澤,性別:男,出生年月:2000年2月,民族:漢,籍貫:河南省濟源市,學歷:大學本科,學校:華北理工大學,學校郵編:063210,專業:金融學

