“火眼金睛”辨模型 解決“線、角”問題靈
文陳 俊
全等三角形判定的關鍵在于認知并熟練掌握全等三角形的幾種判定方法,而難點在于在較復雜的圖形中,靈活運用判定方法找出全等三角形,從而解決“線、角”問題。要迅速找出全等三角形,需要我們熟知全等三角形的常見模型。下面,簡要說明與等腰三角形有關的兩種模型。
一、“手拉手”模型
1.模型說明
如圖1,△ABC、△ADE均為等腰三角形,AB=AC,AD=AE,∠BAC=∠DAE,連接BD、CE,根據“SAS”,易證△ABD≌△ACE。若將△ADE繞點A旋轉一定的角度,如圖2、圖3,則△ABD≌△ACE仍然成立。

圖1

圖2

圖3
該模型是由有公共頂點且頂角相等的等腰三角形構成。“手拉手”模型常應用于旋轉題型,在旋轉變化的同時,始終存在一對全等三角形。
如果把小等腰三角形的腰長看作小手,把大等腰三角形的腰長看作大手,類似大手拉著小手,所以這個模型也被稱為“手拉手”模型。
2.模型應用
如圖4,△ABC、△ADE均為等腰三角形,AB=AC,AD=AE,∠BAC=∠DAE,連接BE、CD交于點F,BE、AC交于點G。求證:(1)BE=CD;(2)∠BFC=∠BAC;(3)連接AF,AF平分∠BFD。

圖4
圖5
證明:(1)∵∠BAC=∠EAD,
∴∠BAE=∠CAD。
在△ABE和△ACD中,
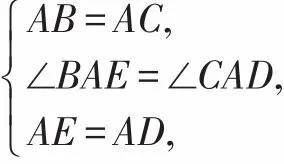
∴△ABE≌△ACD(SAS),∴BE=CD。
(2)∵△ABE≌△ACD,∴∠ABE=∠ACD。
∵在△ABG和△FGC中,∠ABE=∠ACD,∠AGB=∠FGC,∴∠BFC=∠BAC。
(3)如圖5,過點A分別作AH⊥BE、AI⊥CD,垂足分別為點H、I。

∴AH=AI,∴Rt△AHF≌△Rt△AIF。
∴AF平分∠BFD。
小結:本題證明的結論均與“線、角”有關,我們只需挖掘出“手拉手”模型,發現全等三角形,再利用全等三角形的性質解題就水到渠成了。
3.模型拓展——從一般到特殊

圖6

圖7

圖8

圖9
如圖6,若△ABC和△DCE均為等邊三角形,則△CAE≌△CBD;
如圖7,若△ABC和△ADE均為等腰直角三角形,則△ACD≌△ABE;
如圖8,若四邊形ABCD和四邊形AEFG均為正方形,則△ADG≌△ABE。
二、“半角”模型
1.模型說明
如圖9,△ABC中,AB=AC若在△ABC外部作△ABF,且∠4=∠3,AF=AE,則△ABF≌△ACE。
我們習慣把過等腰三角形頂角的頂點引兩條射線,使兩條射線的夾角為等腰三角形頂角的一半的模型稱為“半角”模型。
2.模型應用
如圖10,已知△ABC是等邊三角形,點D是△ABC外一點,DB=DC且∠BDC=120°,∠EDF=60°,DE、DF分別交AB、AC于點E、F。
求證:EF=BE+CF。

圖10

圖11
思路:如圖11,將△BDE繞點D旋轉至△CDG,使△BDE≌△CDG。
∵DB=DC且∠BDC=120°,∴易證∠EBD=∠GCD=90°,F、C、G三點共線。
在△EDF和△GDF中,
∵ED=GD,∠EDF=∠GDF=60°,DF=DF,
∴△EDF≌△GDF,∴EF=GF。
∵GF=GC+CF=BE+CF,∴EF=BE+CF。
3.模型拓展——從一般到特殊
如圖12,在正方形ABCD中,E、F分別是BC、CD邊上的點,∠EAF=45°,求證:(1)EF=BE+DF;(2)C△CEF=2AB。

圖12

圖13
思路:(1)將△ADF繞點A順時針旋轉90°,可得△ABG(如圖13),則△ADF≌△ABG,易證△AGE≌△AFE,∴GE=EF。
∵GE=GB+BE=DF+BE,∴EF=BE+DF。
(2)由(1)得,EF=BE+DF,

小結:利用“半角”模型,先將“半角”兩邊的三角形旋轉到一邊,合并形成新的三角形,接著證明與“半角”所在的三角形全等,最后通過全等的性質得出線段之間的數量關系,從而解決問題。

