基于聲學黑洞的壓電俘能結構系統仿真與優化

汪 恒,鄭偉光，何仕明，陳姍姍

(桂林電子科技大學 機電工程學院, 廣西 桂林 541004)

0 引言

隨著各種無線設備自供能的需求，從環境中采集振動能量成為國內外學者研究的熱門方向[1]。由于振動產生的能量分散，大小不一，如何有效集中采集環境中的振動能成為研究的關鍵。1988年，Mironov[2]提出的一種用來實現對彎曲波振動控制的“聲學黑洞(ABH)”效應，通過結構阻抗的變化，使得結構中波的相速度發生變化，在結構特定區域實現波的能量聚集[3]。聲學黑洞將物理學中的黑洞概念引入到聲振領域，并在振動與噪聲控制及能量收集領域得到廣泛的關注[4-7]。在壓電材料與聲學黑洞結合方面，Remillieux等[8]將壓電分流阻尼技術引入聲學黑洞結構，通過采用負電容電路，實現了全頻段振動控制；Zhao等[9]采用有限元法對壓電俘能結構進行了頻域穩態分析及時域瞬態分析，結果表明，與均質板結構相比，壓電俘能結構具有聲學黑洞結構的壓電換能器在寬頻范圍內有更高能量轉化效率。

目前，很少有學者對具有聲學黑洞結構的壓電俘能系統建立系統電路仿真及負載電阻優化進行研究。本文首先采用有限元法建立具有聲學黑洞的薄板結構壓電耦合模型，對比分析了均勻板及聲學黑洞結構的動能密度及電壓瞬態輸出特性，推導了壓電振子等效電路模型，最后在Multisim軟件中建立壓電俘能全系統等效電路耦合模型，確定外負載最優電阻值，提高系統轉換效率。

1 聲學黑洞結構

在一維結構變化的均勻介質中，彎曲波動方程為

(1)

式中：w為結構橫向位移;D=Eh3/[12(1-ν2)]為彎曲剛度，E為楊氏模量，ν為泊松比；ρ為密度；h為結構厚度；t為時間變量。

對任意一點，x波傳播的振幅可表達為復數形式，即

U(x)=A(x)eiΦ(x)

(2)

其中：

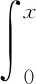
(3)

(4)

式中：Φ為累積相位;kp=ω/cp為均勻板的波數。

對于一個厚度呈現指數形式變化的結構為

h(x)=εxm

(5)

其彎曲方程為

(6)

假設不考慮結構的轉動慣量與剪切效應，波數k為

(7)

式中ω為角頻率。根據c=ω/k可得彎曲波的相速度為

(8)

將薄板按照一定指數進行裁剪，使其厚度變化滿足h(r)=εr2(m≥2),即可形成聲學黑洞。在二維聲學黑洞中隨著厚度的減小，彎曲波的相速度也逐漸減小產生能量聚集效應。當指數m≥2，Φ區域將無限大，波無法到達邊界也無法反射回來，因此彎曲波在邊緣產生聚集。

2 聲學黑洞型壓電俘能器結構

實際薄結構中的厚度不會減小至0，黑洞結構中心存在截斷。本研究在聲學黑洞薄板中心留有一厚度L、半徑r0的圓形平臺，黑洞結構的冪指數變化為h(r)=5×10-4×r2,(r0≤r≤100),結構其他均勻處厚度不變。在板結構的左邊界進行約束，距離固定端邊界L1處的均勻板面上施加點載荷F=Asin(2πft),以距離固定邊界L2處的薄板黑洞結構中心下表層粘貼半徑r0、厚l3的陶瓷壓電片PZT-5H。

3 有限元分析

3.1 參數設置

本研究的薄板材料選用鋁板，壓電片材料選用PZT-5H，結構尺寸及材料參數如表1所示。假設基體部分與壓電層為理想粘結，進行良好的結構應變傳遞。

表1 結構尺寸及材料參數

3.2 仿真分析

通過有限元軟件在0～1 ms時間段進行仿真，每隔0.05 ms選取薄板在應力云圖(見圖1、2)及動能密度圖(見圖3)的周期性變化。

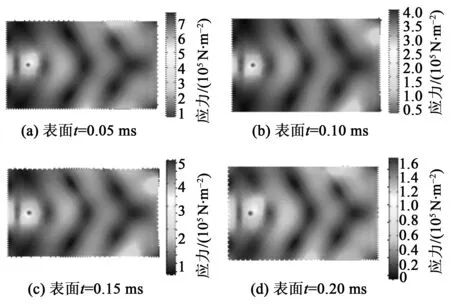
圖1 均勻薄板的應力云圖

圖2 黑洞結構薄板應力云圖

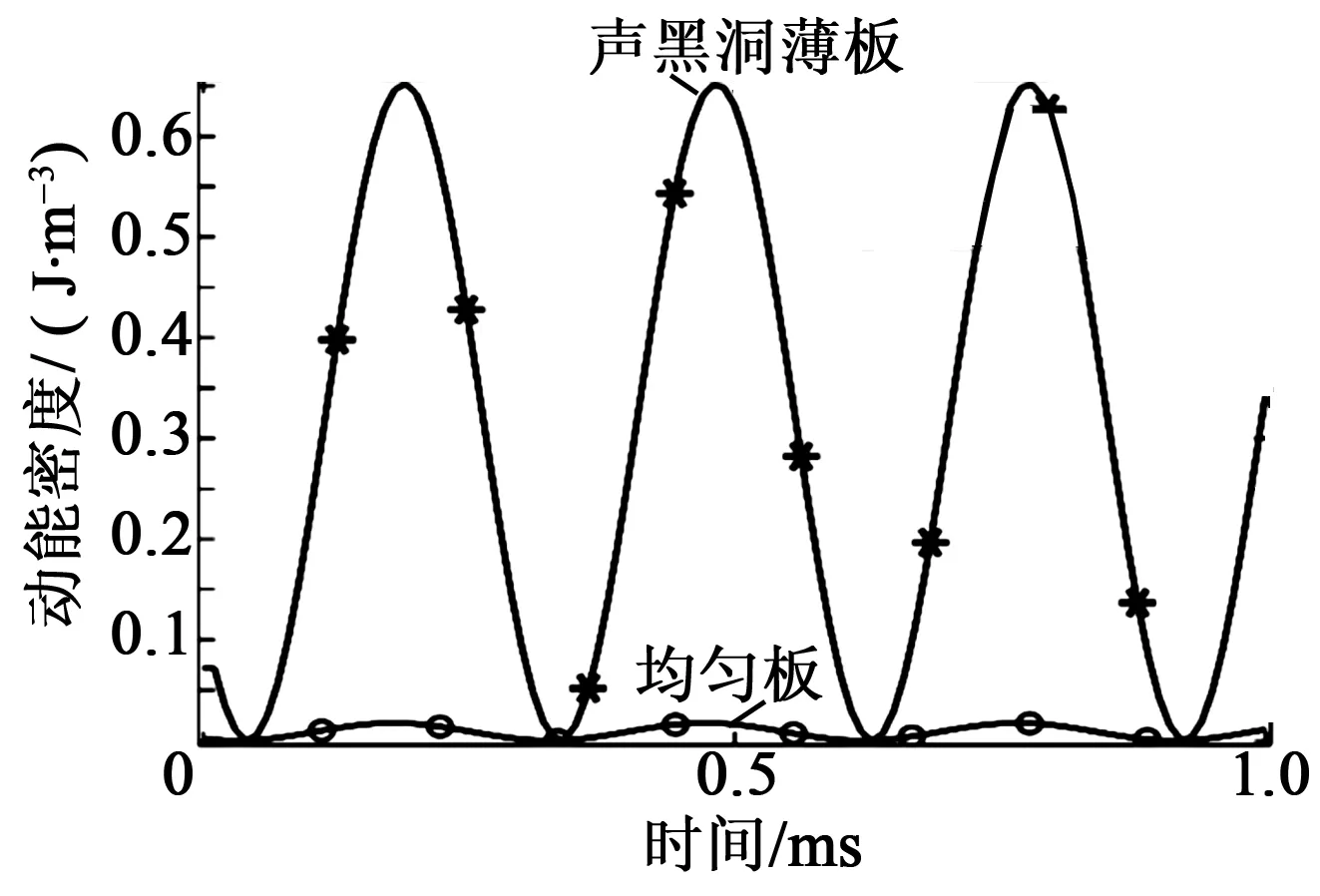
圖3 薄板動能密度對比圖

在建好的模型中分別在兩塊薄板上選取固定位置，其三維坐標為(75,130,5)，施加幅值為3 N的正弦激勵。由圖1～3可看出，聲學黑洞結構薄板在黑洞中心部分有較大的能量聚集效應。選取薄板中心的固定位置(225,130,0)進行動能密度比較，均勻板上動能密度峰值為0.017 4 J/m3，而聲學黑洞結構板的能量密度峰值為0.652 J/m3，從圖3可發現，在0～1 ms時均勻板和黑洞結構的薄板動能密度呈現周期性變化，具有聲學黑洞的動能密度明顯高于均勻板的能量密度。可見，在點載荷的激勵下彎曲波進入黑洞結構區域后波長壓縮，波動幅度增大，振動能量在結構中心進行累積，形成聲學黑洞結構薄板所示的能量集中，圖1～3給出了具體驗證。

3.3 壓電俘能器輸出電壓分析

在兩塊不同結構的薄板表面特定位置粘貼陶瓷壓電片，在不考慮電阻值、壓電片形狀大小等其他變量的影響下，進行有限元軟件的多物理場耦合仿真，兩塊薄板的輸出電壓圖如圖4所示。

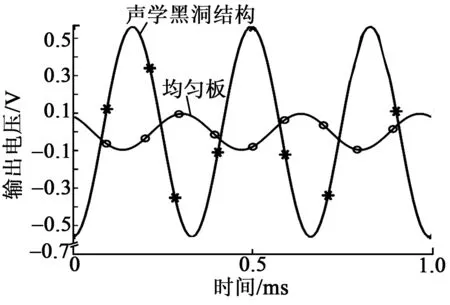
圖4 時域下不同模型的輸出電壓

在相同位置給2塊薄板施加同樣的激勵，在0～1 ms內對其輸出電壓進行分析發現，2塊薄板結構輸出的電壓同樣呈周期性變化，選取2塊板的輸出電壓峰值點，均勻板輸出的最大電壓為0.096 V，聲學黑洞結構薄板輸出電壓峰值達到0.562 V。通過對比，聲學黑洞結構薄板的壓電振子輸出電壓較均勻板提高了近6倍。

4 壓電俘能器全系統耦合

本文通過對壓電振子的結構進行設計，提高了壓電振子的電壓輸出效果，進而提高系統的俘能效率。但實際應用中，壓電俘能器是由壓電振子結構和能量俘獲接口電路共同發揮作用。由于壓電片存在逆壓電效應，外部電路會對結構的振動響應和動力學特性產生影響，同時，壓電振子輸出的交流電壓對電路中轉化的直流電壓產生影響。因此，本研究為了提高壓電俘能器的全系統效率，將壓電振動能量俘獲系統看成一個整體進行優化設計，建立壓電振子等效電路模型和壓電俘能全系統等效電路耦合模型[10]。

4.1 壓電振子等效電路模型

耦合建模中常用的理念方法是通過機械量與電路參數的轉化來表征壓電振動產生的能量。如圖5所示，分別將均勻板和具有聲學黑洞結構的新型壓電振子模型機械參數進行等效電路模型轉化。

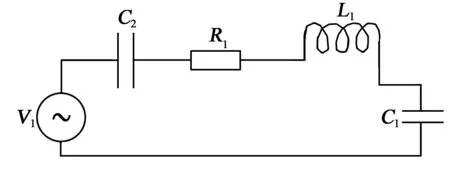
圖5 壓電振子等效電路圖

求解等效電路模型中的參數V1、R1、C1、L1、C2是本研究的關鍵。目前有理論推導、實驗檢測和有限元仿真3種方式。理論推導方法要求幾何形狀規整，實驗測量方法復雜，過程要求高，且有些參數不能直接測量得出。鑒于前面兩種方式的局限性，本研究采用有限元仿真法能有效適用于幾何形狀不規律的壓電振子模型，且能快速準確計算出等效電路參數。

利用現有的壓電振子模型，通過Comsol軟件對其進行短路共振頻率f(C1)、開路共振頻率f(C2)、電荷Q0、短路電壓V(C1)、開路電壓V(C2)仿真計算。

1) 壓電振子短路條件下的共振頻率。在仿真軟件中將壓電振子的輸出端電路短路。在Comsol中進行特征值分析，可得出短路共振頻率f(C1)，且

(9)

2) 壓電振子開路條件下的共振頻率。在仿真軟件中將壓電振子的輸出端不接任何負載構成開路。在Comsol中進行特征值分析，可得出開路共振頻率f(C2)，且

(10)

3) 在上述模型中，將壓電振子在輸出端不接任何負載構成開路，在壓電振子2個電極上施加直流電壓V0,計算產生的Q0，即

Q0=(C1+C2)V0

(11)

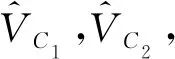
(12)

(13)

由式(9)～(11)可計算C1、L1、C2。由式(12)、(13)可得：

(14)

(15)

由(14)、(15)可計算出V1、R1。

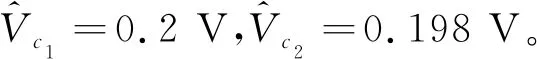
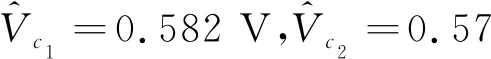
最后根據式(9)～(15)得出壓電振子等效電路模型，如表2、3所示。

表2 均勻板壓電振子等效電路參數估計值

表3 黑洞結構薄板壓電振子等效電路參數估計值

4.2 基于Multisim的全耦合等效電路

壓電振子在振動產生電能的過程中，外部電路負載的大小會影響壓電振子和電路的耦合，進而影響壓電俘能器整體的效果。本研究通過在Multisim建立外接全橋整流電路的振動俘能等效電路模型，重點分析壓電俘能系統外負載電阻對能量轉換率的影響，取0≤R2≤10 000 Ω，確定負載的最優取值范圍。圖6為壓電振子俘能系統等效電路圖。

圖6 壓電振子俘能系統等效電路圖

在外接全橋整流電路，通過仿真可得上述兩種壓電俘能裝置的俘獲功率與負載電阻值的關系，如圖7所示。

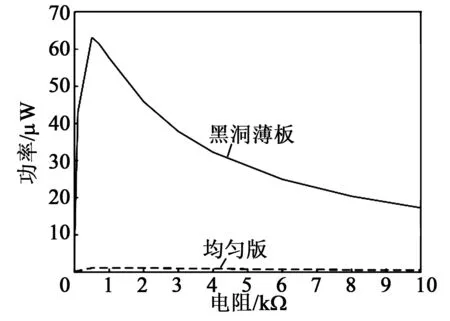
圖7 系統俘能功率與外負載的關系

由圖7可看出，在進行均勻板等效電路仿真時，當外部電阻R2≈1 500 Ω，系統的最優俘能效率可達1.093 μW；在進行聲學黑洞結構薄板等效電路仿真時,當外部電阻R2≈510 Ω，系統的最優俘能效率可達63.098 μW，聲學黑洞結構薄板的壓電俘能裝置系統的轉換效率較均勻板壓電俘能裝置有顯著提高。

5 結束語

本文將聲學黑洞結構引入到壓電俘能器中，通過理論及仿真分析了彎曲波在黑洞結構中聚能效果。在時域上對比分別研究了兩類俘能裝置的表面應力云圖、動能密度圖及輸出電壓圖。結果表明，具有聲學黑洞結構的新型壓電俘能器能夠有效提高薄板的振動能量收集和壓電能量的轉換。同時，利用新型壓電俘能器建立全系統等效耦合電路模型，進行電路仿真分析，確定外負載電阻的最優取值范圍，提高系統能量的轉換效率。本研究的聲學黑洞結構俘能裝置結構簡單，造價低，聚能效果好。結合目前微電子器件和傳感器的自供能需求，聲學黑洞結構俘能器在實際工程應用中具有極大的實用價值。