淺析負反饋調節的數學模型
——以捕食者—獵物種群數量模型為例

周 泉

(湖北省黃石市第三中學 黃石 435000)

人教版高中生物學教材必修3《穩態與環境》給出了反饋調節的概念模型： 在一個負反饋調節系統中，“系統本身工作的作用效果，反過來又作為信息調節該系統的工作”。根據調節機制和作用效應的不同，反饋調節系統分為正反饋調節系統和負反饋調節系統。通過負反饋調節，受控部分的活動向和它原先活動相反的方向發生改變，使系統活動保持穩定。捕食者與獵物種群數量的相對穩定是負反饋調節作用的結果，若以捕食者—獵物種群數量關系為例，建立數學模型，可以獲得兩種曲線圖，即波形圖和循環圖。

1 負反饋調節的波形圖

以時間為橫坐標，種群數量為縱坐標，作捕食者和獵物種群數量隨時間的變化曲線，可以得到由兩條曲線組成的波形圖(圖1)。由圖1可知，曲線N與曲線P間存在“跟隨”關系，即曲線P隨曲線N的變化而發生變化，則曲線N代表獵物種群數量隨時間的變化曲線，曲線P代表捕食者種群數量隨時間的變化曲線。此外，該波形圖顯示出捕食者與獵物的種群數量皆在一定范圍內波動，受負反饋調節作用。

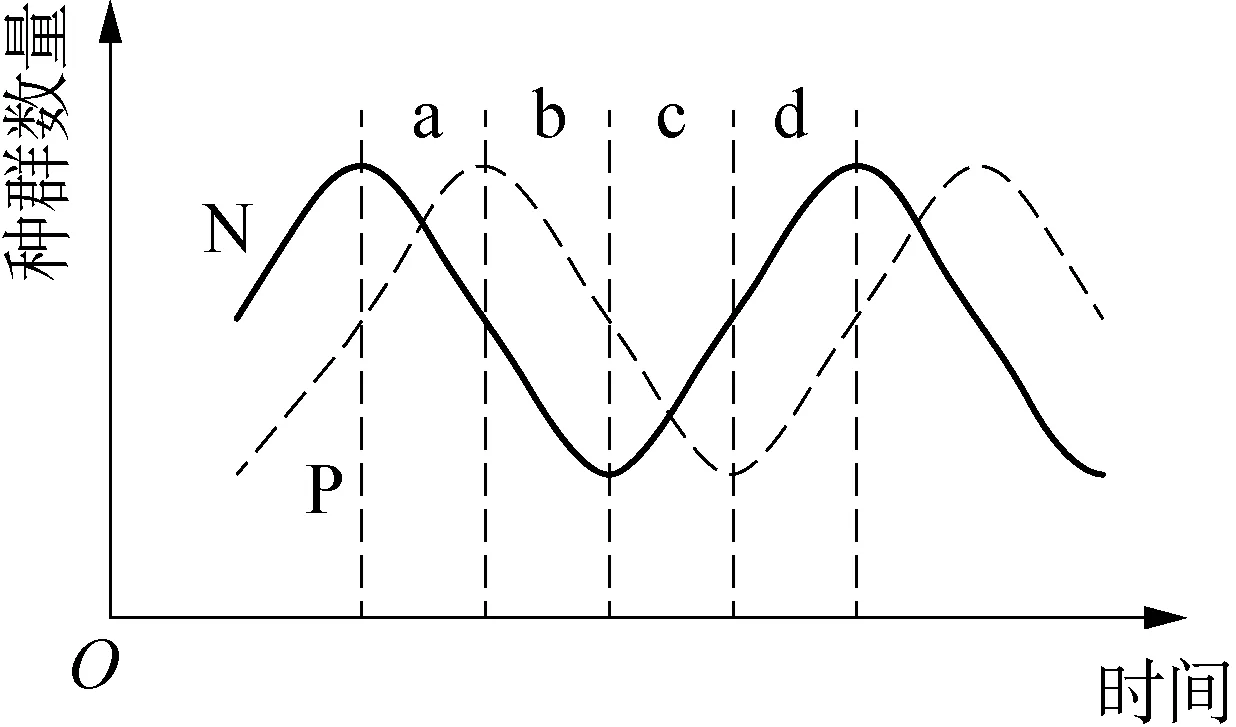
圖1 負反饋調節的波形圖

2 負反饋調節的循環圖

以獵物種群數量為橫坐標，捕食者種群數量為縱坐標，作捕食者種群數量隨獵物種群數量的變化曲線，可以得到逆時針方向圓的循環圖(圖2)。將方向圓均分為四段，分別分析獵物與捕食者的種群數量變化情況。在①區段，獵物種群數量減少，捕食者種群數量增加；在②區段，獵物種群數量繼續減少，捕食者種群數量開始減少；在③區段，獵物種群數量開始增加，捕食者數量繼續減少；在④區段，獵物種群數量繼續增加，捕食者種群數量開始增加，此后依次循環。圖2中的①②③④區段反映的種群數量變化情況依次與圖1中的abcd區段對應。

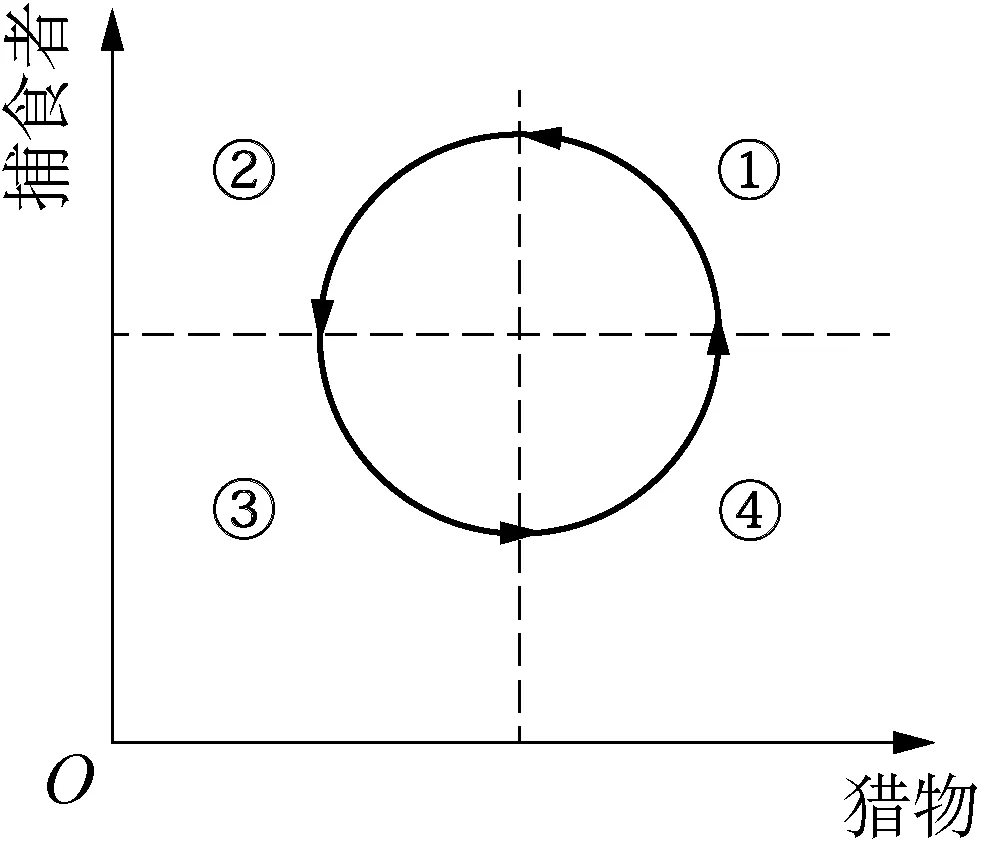
圖2 負反饋調節的循環圖

3 波形圖與循環圖的函數聯系

負反饋調節的波形圖能較直觀地反映出捕食者與獵物的“跟隨”關系，方便判斷曲線的含義。在X、Y軸所示含義未知的情況下，分段描述負反饋調節循環圖中的方向圓，可以轉化為波形圖，進而判斷X、Y軸所示含義。循環圖的分析略顯繁瑣，在此，筆者將利用數學方法進行科學分析，建立波形圖與循環圖的函數聯系。

3.1 逆時針方向圓的轉換 設逆時針方向圓是半徑為1的單位圓，圓心為O點(2， 2)，圓上B點(x，y)以A點(3， 2)為起點逆時針循環運動(圖3)。∠AOB用α來表示，則可得x、y值的表達式：

x=cosα+2，y=sinα+2

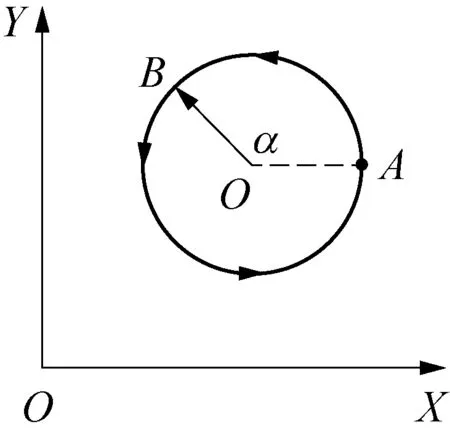
圖3 逆時針方向圓的坐標圖

由x、y值的表達式可知，逆時針方向圓上點的坐標值可分別對應于正弦函數、余弦函數，即可用三角函數曲線表示方向圓。α值與時間值成正比，故以時間為橫坐標、種群數量為縱坐標，可作三角函數曲線(圖4)。進而，可快速判斷曲線X與曲線Y間的“跟隨”關系，即圖3中X軸代表獵物、Y軸代表捕食者。

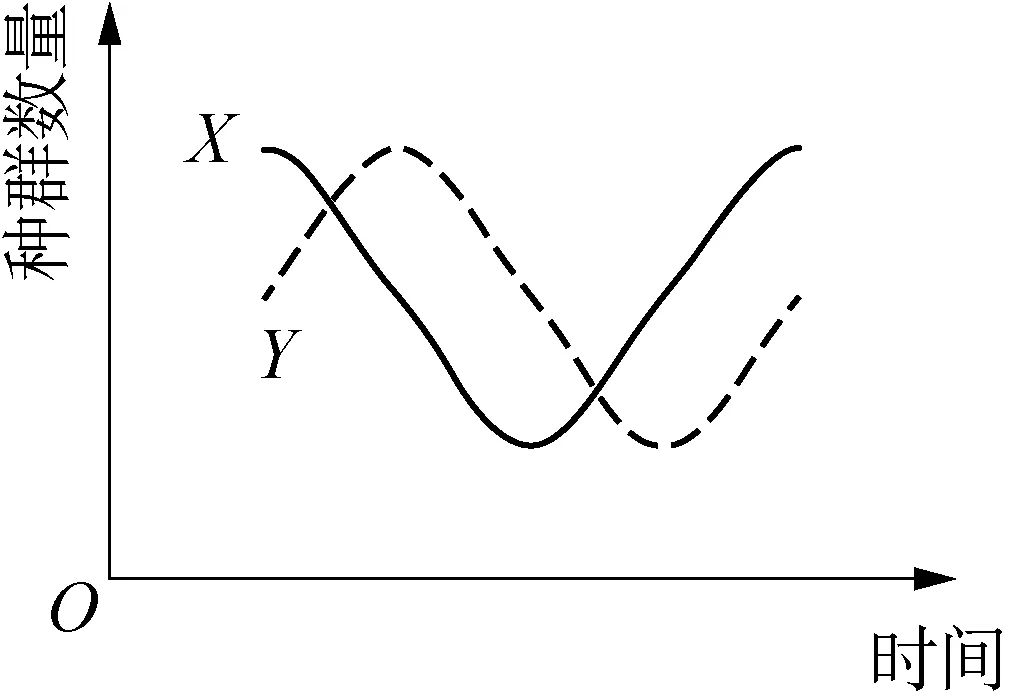
圖4 逆時針方向圓的轉換

3.2 順時針方向圓的轉換 同理，仍設順時針方向圓為單位圓，圓心為O點(2, 2)，圓上C點(x, y)以A點(3, 2)為起點順時針循環運動(圖5)。∠AOC用(2π―α)來表示，則可得x、y值的表達式：

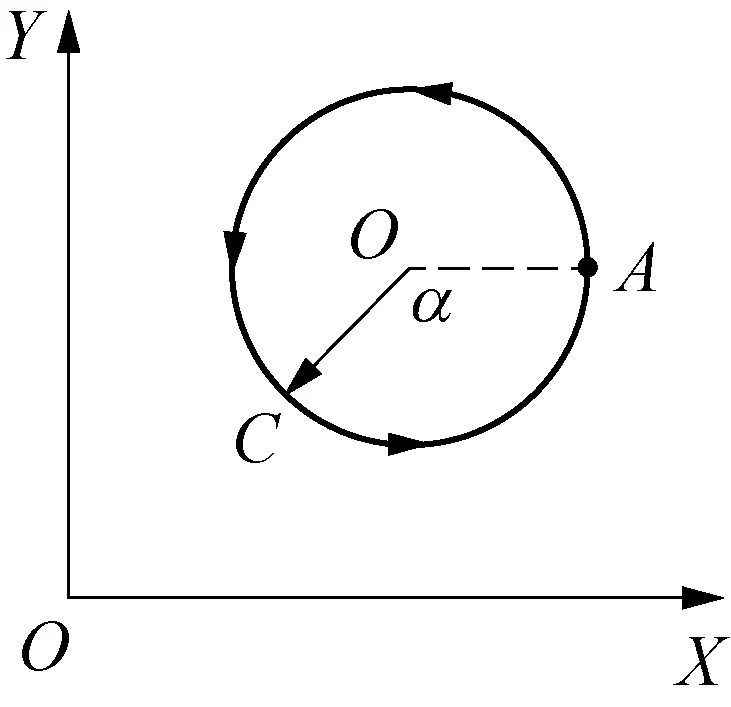
圖5 順時針方向圓的坐標圖

α值與時間值成正比，故以時間為橫坐標，種群數量為縱坐標，依據x、y值的表達式，可將順時針方向圓曲線轉換為三角函數曲線(圖6)。若以波形圖中的曲線X為參照，圖4與圖6中的曲線Y是倒置關系，將導致曲線X與曲線Y“跟隨”關系的改變，即圖5中X軸代表捕食者、Y軸代表獵物。

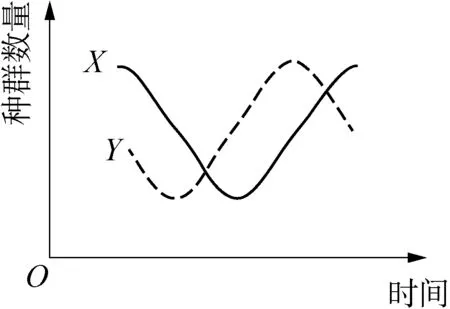
圖6 順時針方向圓的轉換

4 總結

在描述捕食者與獵物間存在的負反饋調節關系時，波形圖是較常使用的數學模型。循環圖直觀性較差，分析起來難度較大，要求學生對方向圓的動態變化作出準確判斷。在X、Y軸所示含義均未給定的情況下，對循環圖進行分析，需注意分析起點的選擇，選定x、y值的最大值或最小值所對應的點為分析起點。此外，在將循環圖轉換為波形圖的過程中，注意對循環圖中單位圓上動點運動方向的處理，不同的方向圓將對應不同含義的X軸與Y軸。