基于深度置信網絡的廣告點擊率預估的優(yōu)化?

陳杰浩，張 欽，王樹良，史繼筠，趙子芊

(北京理工大學 計算機學院，北京 100081)

近年來，互聯網廣告已成為大部分互聯網公司的主要盈利手段，得到了極大的發(fā)展.為了達到最佳互聯網廣告投放效果，廣告點擊率(click-through rate，簡稱CTR)預估成為了計算廣告(computational advertising)[1]領域工業(yè)界和學術界研究的焦點.

廣告精確投放，依賴于預測目標受眾對相應廣告的CTR[2].例如，搜索廣告為互聯網廣告的重要組成部分，該類廣告依據受眾搜索關鍵字的相關性進行廣告投放.廣告投放的變現能力，即廣告此次投放后的期望收益，是決定廣告主是否愿意投放此次廣告的根本依據.千次有效點擊(effective cost per mile，簡稱eCPM)是期望收益的重要指標，其公式為

其中，eCPM為點擊的變現能力，即期望收益；μ為廣告CTR；v為點擊的期望收益.由公式可知，廣告的變現能力由廣告CTR和點擊期望收益決定.由于點擊期望收益與產品本身有關，因此對于廣告投放平臺和廣告主，精確的廣告CTR預估成為了決定廣告變現能力的關鍵.

為提高CTR預估的精確度，本文將深度置信網絡(deep belief net，簡稱DBN)應用于CTR預估領域，進行了大量實證研究，并提出了有效的優(yōu)化策略.本文的主要貢獻總結如下.

(1) 在CTR預估問題中引入DBN，設計了模型結構及訓練方法，通過實驗探討了不同的隱藏層層數、隱含節(jié)點數目對預測結果的影響.

(2) 將本文模型與基于梯度提升決策樹(gradient boost decision tree，簡稱GBDT)和邏輯回歸(logistics regression，簡稱LR)[3]的傳統(tǒng)模型以及模糊深度神經網絡(fuzzy deep neural network，簡稱FDNN)的深度模型進行對比.實驗結果表明，基于DBN的預估方法相比現有的CTR預估算法具有更好的預估精度，在均方誤差、曲線下面積和對數損失函數指標上優(yōu)于GBDT+LR模型2.39%，9.70%和2.46%，優(yōu)于FDNN模型1.24%，7.61%和1.30%.

(3) 為了解決DBN在大數據規(guī)模較大的工業(yè)界解決方案中的訓練效率問題，本文通過實驗證明:CTR預估中DBN的損失函數存在大量的駐點，并且這些駐點對網絡訓練效率有極大的影響.

(4) 為了進一步提高模型效率，從發(fā)掘網絡損失函數特性入手，提出了基于隨機梯度下降算法(stochastic gradient descent，簡稱SGD)和改進型粒子群算法(particle swarm optimization，簡稱PSO)[4，5]的融合算法來優(yōu)化網絡訓練.最終，融合算法在迭代步長小于閾值時可以跳出駐點平面，繼續(xù)正常迭代.實驗證明，使用融合方法訓練深度置信網絡訓練效率可提高30%～70%.

本文第1節(jié)介紹優(yōu)化深度神經網絡(deep neural network，簡稱DNN)訓練效率的兩種主要思路，并結合文獻進行了分析.第2節(jié)提出基于DBN的CTR預估模型，并給出了訓練方式.第3節(jié)設計實驗取得模型參數最佳取值，驗證模型CTR的預估效果.第4節(jié)根據訓練過程討論駐點對DBN訓練的影響，針對駐點的特性，提出基于SGD和PSO的訓練優(yōu)化算法，并通過實驗證明訓練優(yōu)化策略的有效性，進行結果分析.最后總結全文，并對未來值得關注的研究方向進行初步探討.

1 相關工作

1.1 廣告點擊率預估

成熟的CTR預估模型常采用機器學習的方法.Chapelle等人[6]提出了基于LR的CTR預估機器學習框架，主要解決雅虎的CTR預估問題，其采用了4組特征(包含類別特征和連續(xù)特征)作為模型輸入:廣告主特征、網頁出版商特征、用戶特征和時間特征.該框架在LR模型的基礎上加入了參數的二范數正則化項，該方法可以產生更稀疏的模型，使得非零參數增加避免過擬合的問題；本文還提出了針對稀疏數據的哈希方法，通過哈希函數使得原本很稀疏的數據映射到一個固定長度的數據空間中.Facebook[3]于2014年提出了基于GBDT方法，針對其廣告系統(tǒng)進行CTR預估研究，利用用戶的自身信息以及網頁信息等作為特征，由決策樹模型進行模型訓練，得到的輸出結果是一個固定維度的二值向量；而后，使用決策樹模型的輸出結果作為LR模型的輸入重新進行模型訓練，并根據誤差進行權值的調整.這種模型融合的方法結合了非線性決策樹模型能夠擬合非線性特征的特點，以及線性LR模型優(yōu)秀的擴展性、模型訓練速度快的特點.

現有的CTR預估模型發(fā)展比較完備，在經過大量的訓練后均可達到較好的預估效果，但需要人工投入大量精力進行特征的選取、處理與構造工作，廣告數據特征提取不充分，不同特征之間的非線性關聯無法得到充分體現，其預測結果準確程度多與數據分析人員經驗豐富程度正相關.深度學習具有多層非線性映射的深層結構，可以完成復雜的函數逼近，近年來，在計算廣告領域成為研究熱點[7，8].Zhang等人[9]提出一種基于循環(huán)神經網絡(recurrent neural networks，簡稱RNN)的新型CTR預估模型.與傳統(tǒng)模型相比，該模型直接對用戶行為順序進行建模，優(yōu)于LR模型1.11%～3.35%.Chen等人[10]提出了基于長短時記憶模型(long-short term memory，簡稱LSTM)的RNN模型，該模型優(yōu)化了RNN的梯度問題，預測結果優(yōu)于LR模型5%.Jiang等人[11]提出了FDNN模型，該算法基于模糊受限玻爾茲曼機(fuzzy restricted Boltzman machine，簡稱FRBM)和高斯-伯努利受限玻爾茲曼機(Gaussian-Bernoulli restricted Boltzmann machine，簡稱GBRBM)，從原始數據集自動提取隱藏的解釋性信息，放大長尾重要信息，削弱無關信息，預測結果優(yōu)于LR模型3.25%.

然而，RNN模型應用于CTR領域時，需基于用戶或廣告的歷史行為進行時序性建模，現有的廣告數據集大多不包含該類特征，并且在實際工業(yè)運用時采集難度大.

1.2 深度神經網絡訓練效率優(yōu)化算法

由于DNN模型的并行性能相對較差，在訓練數據規(guī)模較大時，其訓練效率是影響網絡性能的關鍵.目前，對網絡訓練效率的研究主要集中于設計更出色的通用優(yōu)化算法和發(fā)掘網絡損失函數特性，并根據特性尋求特定優(yōu)化算法兩個方面.這些方法在DBN的訓練中同樣適用.

1.2.1 通用優(yōu)化算法

在通用優(yōu)化算法[12]方面，Rumelhart等人[13]提出了基于動量(momentum)的優(yōu)化算法，期望使用前一次迭代的信息改進當前迭代的步長；Sutskever等人[14]基于Nesterov的工作提出Nesterov Momentum算法，該算法考慮并嘗試解決了Momentum算法迭代過程中的震蕩問題；Gabriel等人[15]則提出了自適應梯度(adagrad)算法，該算法通過歷史梯度調整學習率，使學習率跟隨梯度變化變化，從而達到調整步長的目的.

1.2.2 針對損失函數特性的優(yōu)化算法

針對損失函數特性的優(yōu)化算法主要挖掘損失函數特性并針對性地進行優(yōu)化[16].在高維空間中，存在各方向梯度均為0的點，被稱為駐點.駐點分為局部極值點與鞍點.近年來，很多研究人員認為，損失函數的局部極值點是影響DNN訓練效率的最大原因.Lo等人[17]對多層感知器中局部極值點的影響進行了研究；Chen等人[18]提出了隨機模糊向后傳播(random fuzzy back-propagation，簡稱RFBP)學習算法，使得迭代時能夠逃離局部值.

然而，最新研究證明:在實際的高維問題中，局部極小值相對數量較少[18，19]:Leonard等人[19]發(fā)現，在某些神經網絡的損失函數中不存在局部極小值；Daniel等人[20]研究表明，高維神經網絡中存在一些局部極小值點，但他們的質量相差不大(即通過不同極值點對應的神經網絡得到的最終預測正確率相差不大)，并且通用優(yōu)化算法(如momentum等)的效果優(yōu)劣并不明確，甚至有時不如最基本的參數調優(yōu)算法.

目前，繼續(xù)挖掘特定DNN模型的損失函數特性、尋找對其訓練效率影響最大的因素并提出解決方案，成為DNN訓練優(yōu)化策略的研究熱點.

2 基于深度置信網絡的廣告點擊率預估模型

2.1 深度置信網絡基本原理

DBN由多個受限玻爾茲曼機(restricted Boltzmann machine，簡稱RBM)堆疊而成.RBM是一個兩層的無向圖模型，結構如圖1所示.RBM可以被用來作為構建DBN的組成部分，它包括一層可視單元和一層隱藏單元，可視單元與隱藏單元之間任意連接，但可視單元、隱藏單元自身沒有連接關系.RBM中的可見層和隱層單元可以是二值節(jié)點，也可以是任意指數族單元，例如高斯單元、泊松單元、softmax單元等.

Fig.1 Structure of RBMs圖1 RBM的結構

DBN最頂的兩層之間是無向連接，稱為聯想記憶層(associative memory)；而其余層與層之間均為有向連接，分為向下的認知權重和向上的生成權重.其結構如圖2所示.

Fig.2 Structure of DBN圖2 DBN結構

本文的研究中，對DBN的學習和訓練包括兩個部分.

(1) 對模型進行無監(jiān)督的預訓練.將DBN每兩層看作一個RBM模型，下層RBM的隱藏層作為上層的可視層，依次進行訓練.最終訓練獲得的參數作為DBN的初始化參數.

(2) 使用Wake-sleep算法，無監(jiān)督地對預訓練之后的模型參數進行調優(yōu).除了頂端的兩層為聯想記憶層之外，網絡中其他層之間的連接均為有向連接，分為自底向上的認知權重和自頂向下的識別權重.調優(yōu)的過程分為“wake”和“sleep”兩個階段.

? “wake”階段是一個識別事物的過程，使用認知權重將底層的輸入樣本數據自底向上的抽象為各層的隱含特征.在此過程中，通過對比散度差算法對生成權重進行調整.在聯想記憶層中進行T步吉布斯采樣，并對聯想記憶層的權重進行調整.

? “sleep”階段是生成樣本數據的過程，使用生成權重自頂向下利用各隱含層抽象出的隱藏特征對輸入樣本數據進行生成重構.

為了避免過擬合，在本文使用的DBN的訓練過程中，采用權值衰減策略(weight-decay).模型各節(jié)點間的權重更新方法如公式(2)所示.

其中，Δwij(t?1)為上一次權重的更新值.模型訓練參數見表1.

Table 1 Training parameters表1 訓練參數

2.2 廣告點擊率預估模型及訓練

本文采用的CTR預估模型為DBN，共分為1個可視層、多個隱藏層和一個輸出層.輸出層使用LR模型進行輸出，整體結構如圖3所示.

CTR預估模型訓練主要分為以下3個階段.

(1) 利用DBN進行深層次的有效特征提取，將降維后的特征數據作為模型的輸入，通過DBN的認知權重，轉化為深層次的抽象特征.

(2) 結合LR模型進行CTR預估.使用DBN模型的最頂層的隱藏層作為LR模型的輸入；同時，在模型的頂層增加一層(包含1個節(jié)點)作為LR模型的輸出；接著，對LR模型進行訓練.

(3) 在對LR模型進行訓練的同時，使用標簽數據，對深度網絡模型的參數進行有監(jiān)督的調優(yōu).將整個網絡模型(包括DBN和LR模型)看作是由向上的認知權重進行連接的標準前饋型神經網絡，模型可視層輸入樣本數據進行前向傳播，而后利用訓練樣本的標簽數據計算模型輸出誤差，使用反向誤差傳播算法(error back propagation，簡稱BP)進行誤差傳播對模型的參數進行進一步調優(yōu).

在整個DBN的模型中，各個節(jié)點的激活函數均采用sigmoid函數，以便引入非線性，并保證數據在傳遞的過程中不發(fā)散.經過處理后的樣本特征數據從模型的可視層進入網絡，經過多個隱藏層的抽象轉化，在模型的頂層形成了深層抽象特征.最后，模型利用DBN提取得到的深層抽象特征作為LR模型的輸入，加入標簽信息，進行CTR的預測.模型的輸出層包含一個sigmoid節(jié)點，其與DBN的頂層隱藏節(jié)點共同構成LR模型.

Fig.3 Structure of CTR prediction model圖3 CTR預估模型結構

模型輸出層節(jié)點的激活概率如公式(3)所示.

其中，x為DBN頂層節(jié)點狀態(tài)，θ為模型輸出層與DBN頂層之間的連接參數，而b則表示輸出層節(jié)點的偏置.

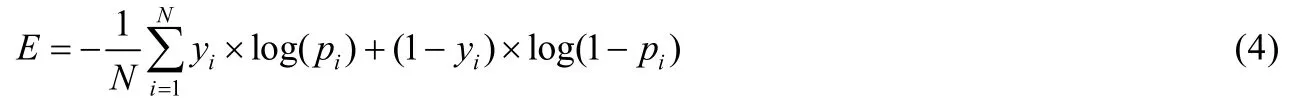
其中，N為測試樣本總數，yi為第i個樣本的目標值(點擊為1，未點擊為0)，1/eix bipθ?+=為第i個樣本模型給出的估計值(預估CTR).使用梯度下降算法可以求出參數θ和b的梯度，如公式(5)和公式(6)所示.

3 廣告點擊率預估實驗

3.1 數據集及衡量標準

本文進行的實驗基于Kaggle數據挖掘比賽平臺的Click-Through Rate Prediction比賽數據集.該數據集由Avazu提供，數據集描述見表2.本文使用數據集中隨機選取的1 000萬條數據，并使用10折交叉法作為實驗驗證方法.

在本文實驗中，針對整體模型CTR預估效果的指標為均方誤差(mean squared error，簡稱MSE)、曲線下面積(area under curve，簡稱AUC)和對數損失函數(LogLoss).針對DBN訓練效率的衡量指標為損失值(loss)、迭代次數(iterations)和訓練時間.

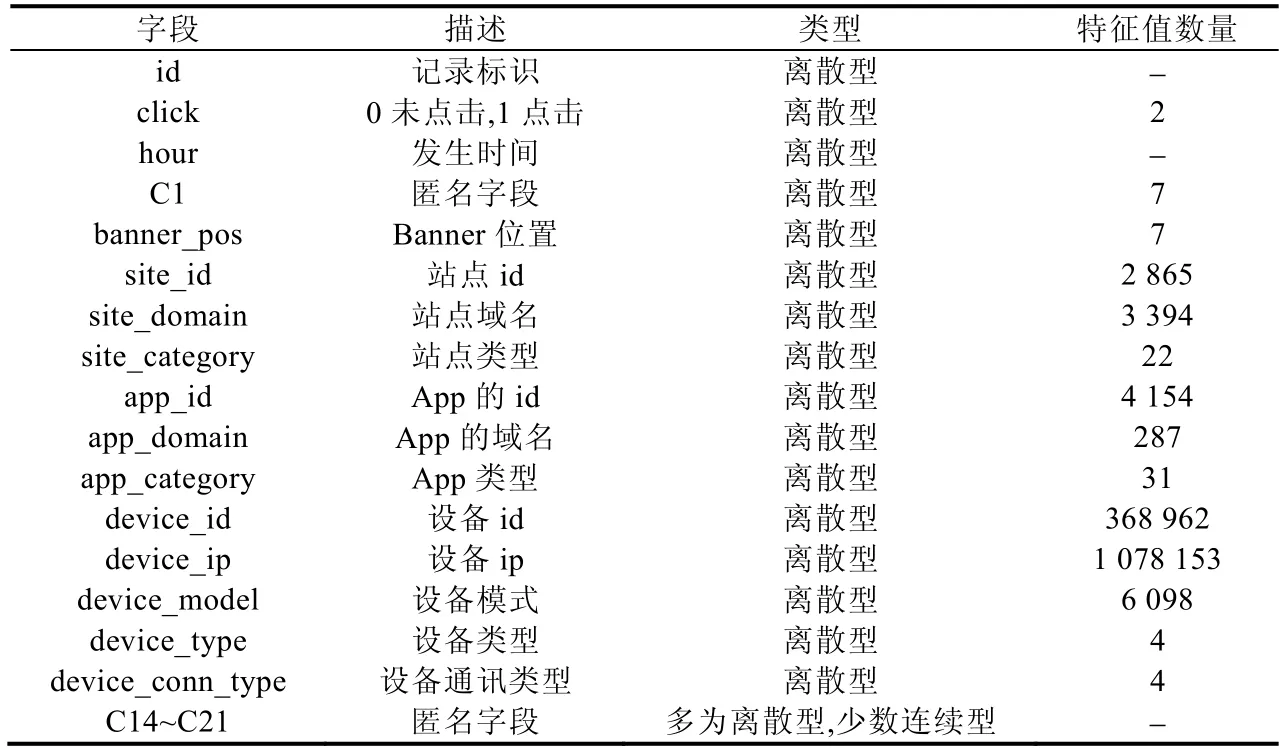
Table 2 Description of dataset表2 數據集描述

3.2 廣告點擊率預估準確率實驗

本節(jié)將首先針對DBN中的重要參數進行單獨實驗，考察不同的參數對預估結果的影響，獲取算法最優(yōu)的預測結果.實驗中，使用AUC指標對不同模型的CTR預估結果進行評估，實驗總共分為3個部分.

(1) 通過實驗，探討DBN隱藏層層數對CTR預估結果的影響.

(2) 通過實驗，對模型逐層驗證不同的隱藏節(jié)點數目對CTR預估結果的影響.

(3) 通過實驗，研究基于DBN的CTR預估模型預估效果.

3.2.1 深度置信網絡隱藏層數實驗

深度模型的隱藏層的個數是模型預估能力關鍵因素，經驗表明，模型的特征表征和提取能力在一定程度上與隱藏層層數正相關；同時，層數越多，深度模型訓練過程越復雜.在實際應用中，通常隱藏層層數的設置要根據實際情況，通過實驗確定.在本節(jié)中，對DBN中隱藏層的層數設定進行實驗分析，在進行實驗的時候，各隱藏層節(jié)點數目均設置為256，逐步添加隱藏層的層數，最終得出的實驗結果如圖4所示.

Fig.4 Curves of the MSE，AUC and LogLoss while training DBN with different hidden layers圖4 用不同隱藏層數訓練DBN的MSE、AUC和LogLoss曲線

隨著神經網絡隱藏層數目的增加，CTR預估準確率出現了明顯的上升，說明在利用深度模型進行深層次特征提取的時候，隱藏層的數目越多，對于輸入層樣本數據特征學習的就越充分，能夠更好地反映數據深層的特征；而當隱藏層數目大于4層時，實驗結果的準確率出現了較快的下滑，說明僅通過增加深度模型的隱藏層數量不能無限制地增加模型預測效果，且進行實驗的過程中隱藏層數目過多，容易導致模型出現過擬合，因此需要通過實驗來確定最合適的隱藏層數目.

3.2.2 深度置信網絡隱藏層節(jié)點數實驗

在本節(jié)中，主要考察DBN模型中各個隱藏層節(jié)點數目對于實驗結果的影響.首先，考察第1層隱藏層對實驗結果的影響，此時固定第2層～第4層隱藏層節(jié)點數為256.實驗結果如圖5所示.

Fig.5 Curves of the MSE，AUC and LogLoss while training DBN with different units in the 1st hidden layer圖5 用不同的隱藏層第1層節(jié)點數訓練DBN的MSE、AUC和LogLoss曲線

在固定隱藏層數和其他層節(jié)點數的實驗中，隨著第1層隱藏層節(jié)點數的增加，實驗結果的準確率逐漸升高.當節(jié)點數大于512時，整體模型同樣出現過擬合的現象，因此512為最佳取值.此時，固定第1層節(jié)點數為最佳取值512，其他層節(jié)點數為256，進行第2層節(jié)點數的實驗，其結果如圖6所示.

Fig.6 Curves of the MSE，AUC and LogLoss while training DBN with different units in the 2nd hidden layer圖6 用不同的隱藏層第2層節(jié)點數訓練DBN的MSE、AUC和LogLoss曲線

隨著隱藏層節(jié)點數的增加，實驗結果的準確率逐漸升高.當節(jié)點數目大于512時，模型同樣出現了過擬合的現象，因此512為第2層節(jié)點數最佳取值.

同理可以得到第3層、第4層隱藏層節(jié)點數目對實驗結果的影響，如圖7和圖8所示.可以看出，第3層、第4層隱藏層節(jié)點數目同樣也應該設置為512.

Fig.7 Curves of the MSE，AUC and LogLoss while training DBN with different units in the 2nd hidden layer圖7 用不同的隱藏層第2層節(jié)點數訓練DBN的MSE、AUC和LogLoss曲線

Fig.8 Curves of the MSE，AUC and LogLoss while training DBN with different units in the 2nd hidden layer圖8 用不同的隱藏層第2層節(jié)點數訓練DBN的MSE、AUC和LogLoss曲線

通過實驗結果可以看出，隨著隱藏層節(jié)點數目的增加，模型CTR預估能力出現了先增后減的現象.這是因為，一方面，隨著隱藏層節(jié)點數目的增加，模型對于樣本數據的隱含特征學習的更加充分；另一方面，如果隱藏層節(jié)點過多的話，容易致使特征學習的過于充分，極度放大不同的特征對預測結果的影響，使得模型對CTR的預測結果過于敏感和不穩(wěn)定.

3.2.3 對比實驗及結果

本節(jié)中進行了本文模型與GBDT+LR及FDNN模型的對比實驗，其中，GBDT+LR模型結構及訓練過程參考文獻[2]，FDNN模型結構及訓練過程參考文獻[6].

利用與第3.2.2節(jié)相似的參數調優(yōu)方法，逐步固定某一參數進行調優(yōu)，取得GBDT+LR以及FDNN模型的最優(yōu)參數，見表3.

Table 3 Bset parameters of GBDT+LR and FDNN表3 GBDT+LR和FDNN模型的最優(yōu)參數取值

最終對比實驗結果如表4所示，本文提出的基于DBN的互聯網廣告CTR模型，CTR預測效果分別在MSE、AUC和LogLoss指標上優(yōu)于GBDT+LR的融合模型2.39%，9.70%和2.46%，優(yōu)于FDNN模型1.24%，7.61%和1.30%.證明了DBN在隱含特征提取和抽象方面更加強大，提取出的深層次特征更能反映事物的本質，這也說明了本文設計的融合模型在互聯網廣告CTR預估的準確率方面達到了預期的實驗效果.

Table 4 MSE，AUC and LogLoss of GBDT+LR，FDNN and DBN表4 GBDT+LR，FDNN和DBN實驗的MSE、AUC和LogLoss指標

3.3 分析與結論

本節(jié)分別進行了DBN隱藏層數實驗、DBN隱藏層節(jié)點數實驗和融合模型與其他模型的對比實驗.隨著隱藏層層數和隱藏層節(jié)點數目的增加，模型對于樣本數據的隱含特征學習的更加充分；隱藏層層數和隱藏層節(jié)點過多，容易致使特征學習的過于充分，極度放大不同的特征對預測結果的影響，使模型對CTR的預測結果過于敏感和不穩(wěn)定.最終，基于DBN的模型CTR預測效果分別在MSE、AUC和LogLoss指標上優(yōu)于GBDT+LR的融合模型2.39%，9.70%和2.46%，優(yōu)于FDNN模型1.24%，7.61%和1.30%.

4 深度置信網絡訓練優(yōu)化策略

在將DNN[21，22]用于訓練數據規(guī)模較大的工業(yè)界解決方案時，常因其有限的并行性而受到訓練效率的制約.作為DNN中的一種，DBN存在著相同的問題.本節(jié)基于網絡損失函數特性，發(fā)現在DBN的損失函數中存在大量嚴重影響訓練效率的駐點.針對這些駐點的特性，提出了一種基于SGD和改進型PSO的網絡訓練優(yōu)化算法.

4.1 駐點對深度置信網絡訓練的影響實驗與結果

駐點包括局部極值點與鞍點.本節(jié)通過實驗分別證明在DBN的損失函數平面中存在這兩種點，以及他們對網絡訓練的影響.

4.1.1 極值點與鞍點判定方式

在數學中，Hessian矩陣是一個多變量實值函數的二階偏導數組成的方塊矩陣，假設有一實數函數f(x1，x2，…，xn)，若函數f的所有二階偏導數都存在，則f的Hessian矩陣的第ij項為

當Hessian矩陣為正定矩陣時，該點為極小值點；當Hessian矩陣為不定矩陣時，該點為鞍點.

4.1.2 局部極值點

局部極值點是指梯度在各方向上都為0，并在鄰域內取值最大或最小的點，在本文研究的問題中，為網絡損失函數的極小值點，而網絡訓練的最終目的在于找到一個達到精度要求的極小值點.本節(jié)通過在梯度下降過程中使用不同訓練算法和不同網絡參數初始值，來對比不同訓練過程和不同初始狀態(tài)下網絡的訓練結果.其結果如圖9、圖10、表5、表6所示.

Fig.9 Curves of the loss while training DBN with SGD and Momentum圖9 用SGD和Momentum訓練DBN的損失曲線

Fig.10 Curves of the loss while training DBN with SGD in different initial parameters圖10 用SGD在不同初值條件下訓練DBN的損失曲線

Table 5 Results while training DBN with SGD and Momentum表5 用SGD和Momentum訓練DBN的結果

Table 6 Results while training DBN with SGD in different initial parameters表6 用SGD在不同初值條件下訓練DBN的結果

由表5、表6可知:不論迭代次數和訓練時間如何，在最終收斂時其MSE、AUC和LogLoss指標相差均小于1%.由此可得出結論:高維網絡最終能夠到達的極值點之間差異不大，只要能夠找到一個可接受的極值點，網絡訓練都可以認為是成功的.

如圖11、圖12所示的是用SGD和Momentum訓練的loss曲線，圖中字母處的小圖代表著各字母點處步長的變化趨勢.先減小后增加的步長趨勢代表著訓練陷入平緩平面并最終跳出.

Fig.11 Curve of the loss while training DBN with SGD圖11 用SGD訓練DBN的損失曲線

Fig.12 Curve of the loss while training DBN with Momentum圖12 用Momentum訓練DBN的損失曲線

兩次實驗中訓練過程在極值點周圍的平緩平面上停留的迭代次數分別達到總次數的37.95%和5%.如圖11點e、圖12點g所示，證明了極值點對訓練效率的影響.

4.1.3 鞍點

鞍點也是各方向梯度等于0的點，但它并非是鄰域內的取值最小值點，即在某些方向上，鞍點可以繼續(xù)訓練下降.實驗測試了使用SGD算法和Momentum算法時的損失函數值下降過程.實驗結果表明:在使用SGD算法和Momentum算法進行訓練的過程中，損失函數值的下降過程存在較明顯的階梯形態(tài)，即過程中會遇到許多鞍點區(qū)域.損失函數停留在這些區(qū)域內浪費了大量的時間[23?25].除圖11點e、圖12點g外，其他點均為鞍點平面.

在使用SGD算法作為優(yōu)化算法的實驗中，在不算最后一次屬于極值點平面的情況下，迭代次數中有24.18%在鞍點平面內，Momentum算法中為54.34%.

4.1.4 分析與結論

一方面，在CTR預估問題的高維網絡中，收斂到的不同極值點對最終結果的影響不大，即不需要太過在意最終收斂解的質量.另一方面，駐點，即極值點與鞍點對網絡訓練的效率影響非常大，總體上，在使用SGD算法時有62.13%、使用Momentum算法時有59.34%的迭代是在駐點平面內進行，這極大地拖累了網絡訓練的效率.

4.2 基于隨機梯度下降和改進型粒子群的訓練優(yōu)化算法

4.2.1 融合方法流程

跳出駐點的判斷標準依靠判斷其Hessian矩陣的正定性，計算復雜度為O(n3)，且在駐點附近的駐點平臺上訓練同樣會被拖慢.根據第3節(jié)的實驗結果，當迭代步長小于0.3時，極有可能陷入駐點平臺.為簡化計算，以判斷步長為激活條件，融合方法使用單次迭代效率較高的SGD算法作為基礎算法，并在陷入駐點平臺時激活PSO算法進行跳出.融合方法的偽代碼如圖13所示.算法流程圖如圖14所示.

Fig.13 Pseudocode of fusion method圖13 融合算法偽代碼

Fig.14 Flowchart of the fusion method圖14 融合算法流程圖

4.2.2 隨機梯度下降算法

SGD算法是最常用的DNN模型優(yōu)化算法之一，發(fā)展成熟，存在較為完善的實現方式，且訓練速度快，故融合算法使用SGD作為基礎優(yōu)化算法.與梯度下降算法(gradient descent)和批量梯度下降(batch gradient descent)算法不同的是:SGD算法計算損失函數的每個參數的偏導數，并在每次迭代時使用單一樣本進行梯度下降.SGD的優(yōu)化函數公式為

其中，θ代表被優(yōu)化的參數，J(θ)為損失函數，α為學習率.當損失函數是方差時，其形式為

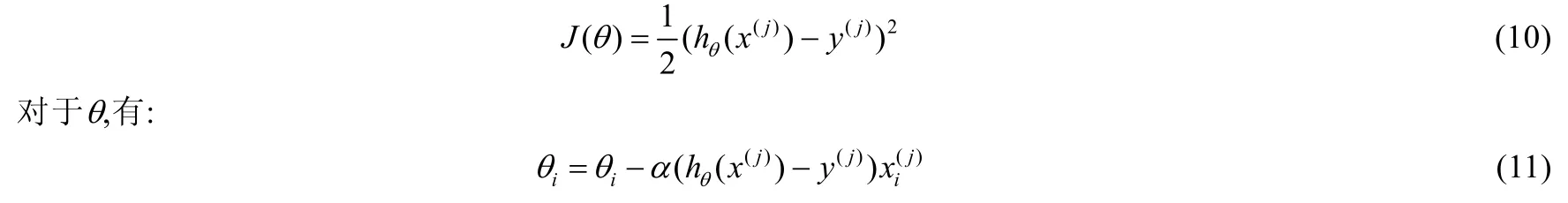
其中，x(j)代表數據集中第j個樣本.

4.2.3 改進的粒子群算法

粒子群算法參數少，易于調整，并具有易實現、收斂快、應用靈活等優(yōu)點，在函數優(yōu)化、神經網絡訓練和模糊系統(tǒng)控制中均有良好的應用效果.本文根據駐點性質，改進了標準版本的PSO算法.引入PSO的目的不在于尋找局部極值點，而是跳出駐點平面.改進的PSO在初始化、迭代和退出判斷等方面均與標準版本不同.

(1) 初始化

改進的PSO算法首先初始化初始粒子P0，其值等于DBN中需要被訓練的參數值.接著，該算法引入沖量[11]的思想初始化一系列如標準PSO中的粒子，使用初始粒子P0的值作為基準值，根據上一次迭代的方向和距離，將每個粒子值的方向設置為在各個維度內與上次迭代方向偏角不超過45°的隨機值，粒子與初始粒子的距離大小為與上一次迭代前進步長相關的隨機值，公式如下:

其中，Addki是第k個粒子的第i個參數的增量，rand(M)是值域為?M，M的隨機函數，LastStep0i為上次迭代時第i個參數的步長，max(Addki)是屬于第k個粒子的所有參數的最大值.

(2) 迭代

迭代過程中，與標準PSO算法相同，記錄每個粒子的歷史最優(yōu)值和所有粒子的歷史最優(yōu)值.算法使用公式(14)和公式(15)計算粒子下一個位置:

其中，speedki指第k個粒子第i個參數此次的迭代步長；w即慣性因子，即此次迭代步長中保留了上一次迭代的慣性；c1，c2分別為個體學習率和全局學習率，分別乘上個體歷史最優(yōu)與當前位置的差，和全局最優(yōu)與當前位置的差；rand是0～1的隨機值.由于希望向外搜索而非向內搜索，本文將學習率設置為大于1的值，此處c1，c2均設置為2.

(3) 退出判斷

由于本文中PSO算法并不需要收斂到一個極值點，而是向外找到一個駐點平面以外的點，考慮兩種情況.

a) PSO算法與梯度算法相比效率較低，為了確保融合算法的整體效率，需要為PSO算法的迭代次數設置上限，即如果在一定次數的迭代后算法仍然沒有找到駐點平面外的點，算法被強行退出.根據實驗經驗，本模型中迭代次數上限為10次.

b) 如果在迭代次數上限之內算法找到了當前駐點平面以外的點，即算法找到的最優(yōu)粒子的損失值與初始粒子P0的損失值相差大于某個閾值，則算法成功運行并退出.根據實驗經驗，此處閾值設為30.

4.2.4 Momentum優(yōu)化算法

Momentum算法是基于動量的優(yōu)化算法，核心思路在于在當前梯度上加入上一次迭代的動量，即

其中，Δxt為本次迭代步長，Δxt?1為上次迭代步長，η為學習率，gt為此次迭代梯度，ρ為上一次迭代的動量參數.本文使用Momentum優(yōu)化算法作為對照組，考察融合算法的優(yōu)化效果.

4.3 訓練優(yōu)化算法的實驗與結果

學習率是一個重要的超參數，它控制著基于損失梯度調整神經網絡權值的速度，大多數優(yōu)化算法對它都有涉及.學習率越小，沿著損失梯度下降的速度越慢.從長遠來看，這種謹慎慢行的選擇比較保守，但可以避免錯過任何局部最優(yōu)解.然而，過小的學習率也意味著收斂速度變慢.本節(jié)將討論不同學習率下訓練優(yōu)化算法的效果.

4.3.1 較小學習率實驗

如圖15所示為學習率0.008(較小學習率)時，網絡在使用SGD算法，Momentum算法和新融合算法作為優(yōu)化函數時損失函數值的下降過程.

Fig.15 Curves of the loss while training DBN with SGD，Momentum and SGD+PSO (learning rate 0.008)圖15 用SGD，Momentum及SGD+PSO訓練DBN的損失曲線(學習率為0.008)

從圖中可知，不同算法訓練Loss下降速度不同.SGD算法與SGD+PSO算法Loss曲線存在兩次交點，在迭代次數小于第1次交點時，融合算法下降速度快；此后，單一SGD算法下降速度反超.但在Loss值逼近2 000時，單一SGD算法下降趨于平緩，陷入了駐點平面；而融合算法通過改進型PSO算法跳出平緩平面，從而繼續(xù)正常下降.3種算法的詳細表現情況見表7.

Table 7 Detailed result of training DBN with SGD，Momentum and SGD+PSO (learning rate 0.008)表7 用SGD，Momentum及SGD+PSO訓練DBN的詳細結果(學習率為0.008)

如圖16所示是在使用這3種算法時每次迭代損失函數下降幅度的log值.在相同的參數下，使用新算法進行優(yōu)化時每次迭代下降幅度都可以控制在閾值以上.如圖8所示，此處閾值為0.3，則新算法下降幅度的log值均大于?0.5.這證明融合算法可以極大地減少網絡需要迭代的次數和時間.具體地，使用了融合算法的優(yōu)化過程迭代次數是僅使用SGD算法的62.34%，迭代用時是僅使用SGD算法的75.87%.

Fig.16 Curves of log(Δloss) while training DBN with SGD，Momentum and SGD+PSO (learning rate 0.008)圖16 用SGD，Momentum及SGD+PSO訓練DBN時每次迭代loss的log值(學習率為0.008)

4.3.2 較大學習率實驗

在學習率為0.02(較大學習率)時，SGD，Momentum和SGD+PSO算法的訓練過程和結果如圖17所示.

Fig.17 Curves of the loss while training DBN with SGD，Momentum and SGD+PSO (learning rate 0.02)圖17 用SGD，Momentum及SGD+PSO訓練DBN的損失曲線(學習率為0.02)

如表8所示為3種算法的詳細表現情況.在學習率較大的情況下，單一SGD算法和Momentum算法在迭代過程中都出現了Loss值升高的情況，而融合算法保持持續(xù)下降態(tài)勢，證明了融合算法更適應激進的學習策略.融合算法的總迭代次數是單獨使用SGD算法的22.35%，運行總時間是SGD算法的35.09%.同時，融合算法迭代次數是單獨使用Momentum算法的37.15%，運行時間則縮短為44.85%.

Table 8 Detailed result of training DBN with SGD，Momentum and SGD+PSO (learning rate 0.02)表8 用SGD，Momentum及SGD+PSO訓練DBN的詳細結果(學習率為0.02)

如圖18所示是3種算法每次迭代loss的log值，對比圖17可以看出，明顯出現了振蕩現象.

Fig.18 Curves of log(Δloss) while training DBN with SGD，Momentum and SGD+PSO (learning rate 0.02)圖18 用SGD，Momentum及SGD+PSO訓練DBN時每次迭代loss的log值(學習率為0.02)

4.3.3 分析與結論

本文提出的DBN模型訓練優(yōu)化融合算法使用SGD作為基礎優(yōu)化算法，該算法是最常用的DNN模型優(yōu)化算法之一，發(fā)展成熟，存在較為完善的實現方式，訓練速度快.而作為跳出算法的PSO算法參數少，易于調整，并具有易實現、收斂快、應用靈活等優(yōu)點，在函數優(yōu)化、神經網絡訓練和模糊系統(tǒng)控制中均有良好的應用效果.針對駐點特性，在將PSO算法的初始化、迭代和退出判斷進行改進之后，本文提出的融合算法在迭代步長小于閾值時激活改進型PSO算法跳出駐點平面，減少訓練過程中的震蕩，提升整體訓練效率.

在較小學習率和較大學習率實驗中，實驗結果均證明了本文融合算法的有效性，算法效率在迭代次數和迭代時間方面均有較大提升.從圖17中可以得到結論:當學習率較小，每次迭代時loss的下降幅度較小.相對地，圖18中顯示出較大的學習率會激化訓練時的震蕩.

學習率越大，改進型PSO算法的采用便越多，融合算法對訓練的影響便越大.大的學習率也意味著SGD算法部分更加激進，在地形復雜程度較小的前中期，SGD算法的優(yōu)化效率自身就可以更高；而當到達地形較為復雜的空間，網絡損失函數值的下降幅度一旦有減小的趨勢，即訓練效率有惡化的跡象時，較大的學習率會使得損失值下降幅度在更少的迭代次數內下降得足夠小，甚至產生震蕩，而這會導致改進型PSO算法的調用.相反，在學習率較小時，相鄰迭代的損失值下降幅度變化較小，從較大下降幅度下降到調用改進型PSO算法的閾值需要的迭代次數較多，這一定程度上降低了融合算法的效率.

通過加大學習率來提高融合算法的優(yōu)化效率并非無限制的，更高的學習率會導致傳統(tǒng)算法震蕩現象的大量出現，因此，過大的學習率本身沒有任何實用和對比意義.另外，學習率的提高會使得改進型PSO算法調用頻率的增加，而改進型PSO算法的迭代效率低于SGD算法，這會導致網絡整體迭代效率的下降.

5 總結與展望

本文引入DBN進行CTR預估，給出了其結構及訓練方法，通過實驗探討了不同的隱藏層層數，隱含節(jié)點數目以及迭代周期對預測結果的影響，并與其他模型的預估結果進行對比分析，實驗證明了使用DBN作為構造模型的融合模型相比現有的CTR預估常見算法具有更好的CTR預估效果，預估精度在MSE、AUC和LogLoss指標上優(yōu)于GBDT+LR模型的融合模型2.39%，9.70%和2.46%，優(yōu)于FDNN模型1.24%，7.61%和1.30%.

優(yōu)化策略方面，通過實驗證明了在CTR預估問題的DBN模型中，駐點對網絡訓練效率和結果有很大的影響.接著，本文從發(fā)掘DBN損失函數特性入手，針對駐點特征，提出了一種結合了SGD和PSO的融合算法.該融合算法在迭代步長小于閾值時可以跳出駐點平面，繼續(xù)正常迭代.最終實驗結果表明，融合算法能夠很好地結合SGD的高效與PSO的梯度無關性，在不影響網絡訓練結果的前提下，提高了網絡訓練的效率30%～70%.

本文提出的融合算法仍有一些后續(xù)工作值得擴展:(1) 在DNN的訓練中，如何系統(tǒng)科學地設置學習率已是研究人員的研究重點[26，27]，也是本文提出的融合算法的關鍵參數之一；(2) 本文使用閾值方法判斷駐點和駐點平面，下一步本文考慮引入自適應方法，進行該閾值的動態(tài)調節(jié)；(3) 引入更多的應用場景，考察本文提出的融合算法對于其他應用場景中的DBN乃至DNN是否存在普適性，以及本文研究結論的一般性.