Midori-64 算法的截斷不可能差分分析?

李明明, 郭建勝, 崔競一, 徐林宏

(信息工程大學,河南 鄭州 450001)

不可能差分分析,由Knudsen[1]和Biham[2]兩人分別獨立提出,是目前最常用的密碼分析方法之一.Kim 等人[3]提出了μ方法.該方法通過計算機搜索找出各種算法結構中所固有的不可能差分形式,這些固有的不可能差分只與算法的結構有關,而與算法所采用的S盒無關,這也就是所謂的截斷不可能差分.后來,Luo 等人[4]在μ方法的基礎上改進,提出了UID 方法.不同于μ方法,UID 方法利用中間相錯的思想將密碼算法結構分解成兩部分進行處理.此外,孫兵等人[5]基于整環上的矩陣論證明了SPN 結構及嵌套SPN 的Feistel 結構的截斷不可能差分區分器的上界取決于線性層的本原指數,并以AES 算法、ARIA 算法和Camellia 算法為實例,分別證明了AES 算法和ARIA 算法的截斷不可能差分區分器都至多4 輪、Camellia 算法(不考慮FL/FL?1層)不可能差分區分器至多8 輪.

隨著物聯網的不斷發展,物聯網的安全問題日益嚴峻.由于物聯網上的加密器件大多存儲空間小、計算能力弱,因此,傳統的密碼算法不適合用來保護物聯網上的信息安全.在這種情況下,大量輕量級密碼算法應運而生,典型的算法有PRESENT[6],MIBS[7],GOST[8],KLEIN[9],LED[10],Piccolo[11],LBlock[12],PRINCE[13]等.

這些輕量級密碼算法大部分關注的是硬件實現電路的面積,但Banik 等人[14]認為,制約輕量級算法應用的因素是算法的功耗,低功耗的密碼算法能夠更為廣泛地應用于多種設備中,并在Asiacrypt 2015 會議上提出專注于低功耗的Midori 算法.由于Midori 算法受限于輕量級使用環境,故通常不對其在已知密鑰、相關密鑰、選擇密鑰條件下的安全性進行分析,更多考察算法在單密鑰條件下的安全性.

目前,對于Midori 算法在單密鑰條件下有多個安全性分析結果.2017 年,Lin 等人[15]利用中間相遇攻擊方法,通過構造5 輪與6 輪區分器,分別給出了10 輪～12 輪Midori-64 算法的安全性分析結果.2015 年,Guo 等人[16]對Midori-64 算法的弱密鑰集進行了分析,利用Subspace 攻擊給出了全輪Midori-64 算法的分析結果;2017 年,Chen等人[17]構造了第一個6 輪截斷不可能差分區分器,并給出首個不含入口白化密鑰的10 輪Midori-64 算法不可能差分分析.

Midori 算法的設計者曾估計:在單密鑰條件下,該算法不可能差分區分器的最大輪數是7 輪,其7 輪或7 輪以上截斷不可能差分區分器是否存在,是尚未解決的問題.若存在,可以利用該不可能差分區分器分析更高輪數Midori 算法;若不存在,如何將Midori 算法6 輪截斷不可能差分區分器都找出來并進行分類,及是否存在更優的區分器使得對Midori-64 算法分析結果更好.這些問題就是本文研究的重點.

本文首先證明了在單密鑰條件下,Midori 算法截斷不可能差分區分器的輪數至多6 輪,并根據該證明過程,對6 輪截斷不可能差分區分器進行了分類;其次,根據Midori 算法6 輪截斷不可能差分區分器的分類,構造了一個6 輪區分器,并給出了11 輪Midori-64 算法的不可能差分分析,恢復了128 比特主密鑰.本文得到的結果與在單密鑰條件下現有分析結果對比見表1.

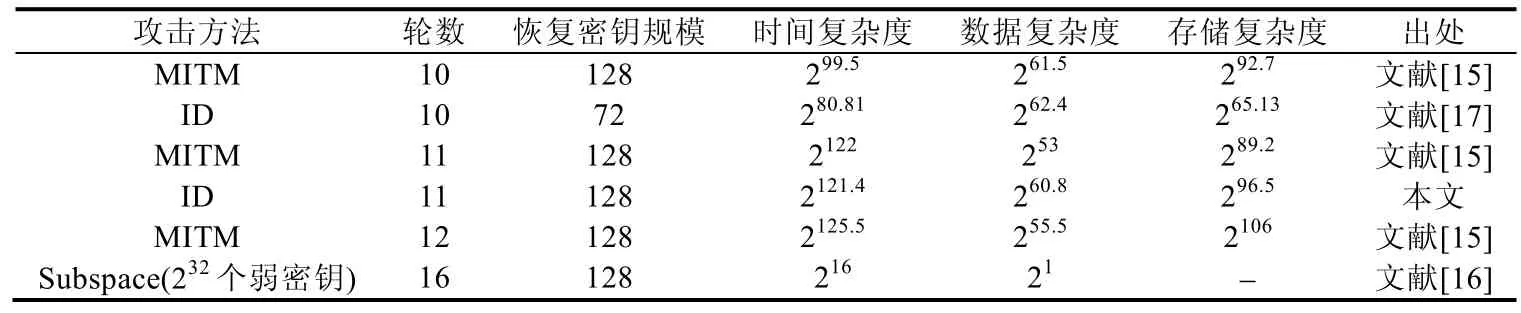
Table 1 Comparison of attacks on Midori-64表1 Midori-64 算法分析結果對比

本文第1 節主要介紹Midori 算法及其相關性質.第2 節證明Midori 算法截斷不可能差分區分器至多6 輪.第3 節對Midori 算法的6 輪截斷不可能差分區分器進行分類.第4 節給出11 輪Midori-64 算法的不可能差分分析.第5 節總結全文.

1 Midori 算法介紹

1.1 符號說明

·P:明文.

· ΔC:輸出密文差分.

·xi:第i輪經過密鑰異或后的狀態.

·yi:第i輪經過非線性變換后的狀態.

·zi:第i輪經過移位變換后的狀態.

·wi:第i輪經過列混合變換后的狀態.

·kei:第i輪加密密鑰.

·kei[j]:第i輪加密密鑰第j個字節.

1.2 Midori算法

Midori 算法分為Midori-64 與Midori-128 兩種,密鑰規模都是128 比特,分組規模分別為64 比特與128 比特,對應的迭代輪數為16 輪與20 輪.分組狀態表示為16 個比特塊的形式,分組規模為64 比特時,每個比特塊為半字節;分組規模為128 比特時,每個比特塊為字節,如圖1 所示.

Fig.1 State of Midori圖1 Midori 分組狀態

Midori 算法采用SPN 結構,其輪函數依次由非線性變換SubCell、移位變換ShuffleCell、列混合變換MixColumn、密鑰異或KeyAdd 這4 個變換組成.這4 個變換及密鑰擴展算法的具體介紹如下.

· 非線性變換SubCell:在Midori 算法中共有2 個不同的對合4 比特S盒Sb0,Sb1,即Sb0,Sb1:{0,1}4→{0,1}4.在Midori-64 中使用一個S盒Sb0.在Midori-128 中使用由兩個Sb1與4 個不同的置換生成4 個8 比特的S盒Sb0,Sb1,Sb2,Sb3.Sb0,Sb1以16 進制表示形式給出,見表2.

Table 2 S-boxes Sb0,Sb1 of Midori表2 Midori 中使用的S 盒Sb0,Sb1

· 移位變換:將16 個比特塊的順序進行重新排列,其變換及逆變換具體如下:

· 列混合變換:使用對合二元陣M對狀態中每一列進行如下操作,即M?(si,si+1,si+2,si+3)′→(si,si+1,si+2,si+3)′,

其中,i=0,4,8,12,M及其逆矩陣M?1如下:

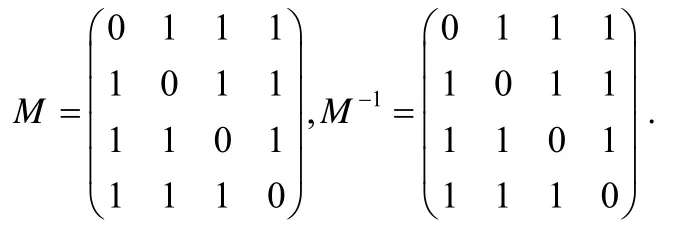
· 密鑰異或:將狀態字節與密鑰字節對應位置進行模2 加運算.

密鑰擴展算法:Midori 算法使用128 比特主密鑰,其密鑰擴展算法較為簡單.其中,Midori-64 算法將128 比特主密鑰分為兩部分K=k0||k1,算法的入口與出口白化密鑰均為WK=k0⊕k1,圈子密鑰kei=k(i+1)mod2⊕αi,1≤i≤15,其中,αi是輪常數.而Midori-128 算法的入口與出口白化密鑰均為WK=K,圈子密鑰kei=K⊕βi,1≤i≤19,其中,βi為輪常數.且當1≤i≤15 時,滿足αi=βi.

Midori 算法的加密需要在算法的初始位置異或一個白化密鑰WK,為確保Midori 算法加解密算法結構相似性,算法在最后一輪省略移位變換與列混合變換.16 輪Midori-64 算法的加密流程如圖2 所示.

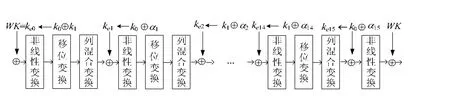
Fig.2 Encryption process of Midori-64圖2 Midori-64 算法加密流程

1.3 Midori算法相關性質

性質1.1.在Midori-64 算法中,若已知白化密鑰,當再得到任意一個奇數輪圈子密鑰或者任意一個偶數輪圈子密鑰時,即可恢復主密鑰;在Midori-128 算法中,若已知任意一個圈子密鑰,則可以恢復主密鑰.

性質1.2[15].給定Midori 算法S盒的一對對應的輸入、輸出差分,平均可以確定一對S盒的輸入與輸出.

性質1.3[18].對于Midori 算法列混合變換,當輸入狀態的某列僅有1 個比特塊差分活動時,輸出狀態必在相同列的其余3 個比特塊有差分活動,且差分值相等;當輸入狀態的某列有兩個比特塊差分活動且兩個差分值相同,則輸出狀態必定與輸入狀態相同;當輸入狀態的某列有3 個比特塊差分活動且差分值相同,則輸出狀態僅在相同列的另一個比特塊上差分活動.

性質1.4.原在同一列的半字節,經兩次Midori 算法移位變換后,必定在同一行:

性質1.5.設yi僅在某一列有3 個比特塊差分活動(差分值可能不同),則yi經一輪Midori 算法加密,再經一次移位變換后輸出狀態zi+1必定其中3 列有兩個比特塊差分活動,一列有3 個比特塊差分活動.

證明:yi經移位變換輸出狀態zi在不同的3 列各有一個比特塊差分活動.再經列混合變化輸出狀態wi.其中,3列有3 個比特塊差分活動,其余一列沒有差分活動比特塊.由于經密鑰異或變換及非線性變換不改變原狀態截斷差分活動位置,故yi+1的差分狀態與wi一致.對于yi+1經移位變換的輸出狀態zi+1,不妨先考慮yi+1+zi經移位變換后的輸出狀態.因為yi+1+zi滿足其中3 列每比特塊都有差分活動,其余一列沒有差分活動比特塊,故經SC變化輸出狀態必定每一列都有3 個比特塊差分活動.又因為由性質1.4 可知,zi再經一次移位變換后輸出狀態有差分活動的比特塊必定在同一行,所以zi+1必定其中3 列有兩個比特塊差分活動,一列有3 個比特塊差分活動.□

性質1.6.設yi僅在某一列有2 個比特塊差分活動(差分值可能不同),其余列沒有差分活動比特塊,則yi經一輪Midori 算法加密,再經一次移位變換后輸出狀態zi+1必定其中兩列各有兩個比特塊差分活動,其余兩列各有一個比特塊差分活動.

證明過程與性質1.5 的證明類似,故略.

2 Midori 算法截斷不可能差分區分器最大輪數的分析

2016 年,Chen 等人在單密鑰條件下構造了第一個6 輪截斷不可能差分區分器.對于7 輪及7 輪以上截斷不可能差分區分器是否存在,是本文研究的重點內容之一.

對于Midori 算法截斷不可能差分區分器至多6 輪的證明的基本思想:證明任意(非零)初始差分狀態經過3.5 輪Midori 算法加密或者3.5 輪Midori 解密算法后的輸出狀態的每個比特塊都可能差分活動,這樣就不可能構造出7 輪或者7 輪以上的截斷不可能差分區分器.當然,7 輪截斷不可能差分區分器不僅僅只能由向下加密3.5 輪、向上解密3.5 輪的差分路徑組成,也可以由加密(解密)4.5 輪和解密(加密)2.5 輪的差分路徑構成,但由于若某個狀態其每個比特塊都可能存在差分活動,該狀態再經1 輪加密或解密Midori-64 算法,輸出狀態必定不存在確定差分活動或差分不活動的比特塊,這樣就不能構成一條截斷不可能差分區分器.所以,只需證明任意初始差分狀態經過3.5 輪Midori 算法加密或者3.5 輪Midori 解密算法后的輸出狀態的每個比特塊都可能差分活動即可.

為便于區分器的分類,不妨以狀態z1為初始輸入狀態,按加密過程和解密過程,證明分為第2.1 節與第2.2節兩部分.

2.1 Midori算法加密過程差分路徑

引理2.1.初始輸入狀態z1只在某一列存在差分活動的比特塊時,經過3.5 輪Midori 算法加密后,輸出狀態w4的每個比特塊都可能差分活動.

為證明該引理,分別討論初始輸入狀態z1只在某一列存在1 個差分活動、2 個差分活動、3 個差分活動、4個差分活動比特塊這4 種情況.本文中如不加特殊說明,我們考慮的初始狀態z1其差分活動比特塊的差分值都是相同的,這是因為差分值不同先于差分值相同的情況輸出每個比特塊都可能差分活動的狀態.由于KeyAdd不改變原狀態截斷差分活動位置,為表述簡潔,性質2.1～性質2.4 中都省去了最后1/4 輪.

性質2.1.初始輸入狀態z1只存在1 個差分活動比特塊時,經過2.5 輪Midori 算法加密后,輸出狀態w3的每個比特塊都可能差分活動.

證明:設z1唯一的差分活動比特塊在第i列,其中,0≤i≤3.z1經3/4 輪Midori 算法加密后,非線性變換SB輸出狀態y2必定僅在第i列有3 個比特塊差分活動.以z1僅在第6 個比特塊有差分活動為例,給出其2.5 輪Midori算法加密過程,如圖3 所示,其中,白色表示差分為0 的半字節,黑色表示差分活動的半字節,斜線表示可能存在差分的半字節.

由性質1.5 可知,y2經一輪Midori 算法加密后,再經SC,輸出狀態z3必定其中3 列有兩個比特塊差分活動,一列有3 個比特塊差分活動.z3再經MC,輸出狀態w3的每個比特塊都可能差分活動.證畢.□

性質2.2.初始輸入狀態z1只在某一列存在2 個比特塊差分活動時,經過3.5 輪Midori 算法加密后,輸出狀態w4的每個比特塊都可能差分活動.

證明:z1經3/4 輪Midori 算法加密后,輸出狀態y2必定僅在某一列有2 個比特塊差分活動,其余列沒有比特塊差分活動.以z1僅在第5、第6 個比特塊有差分活動為例,給出其3.5 輪Midori 算法加密過程,如圖4 所示.

由性質1.6 可知,y2經一輪Midori 算法加密后,再經一次SC,輸出狀態z3必定其中兩列各有兩個比特塊差分活動,其余兩列各有一個比特塊差分活動.故易知:再經1.5 輪,輸出狀態w4不存在確定有無差分活動的比特塊.證畢.□

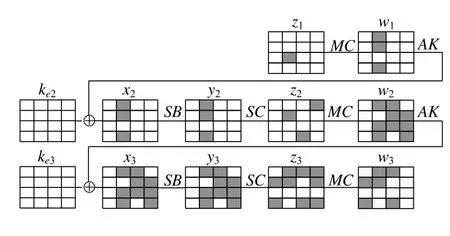
Fig.3 2.5-round differential path of Midori in encryption direction I圖3 2.5 輪Midori 算法加密方向差分路徑I

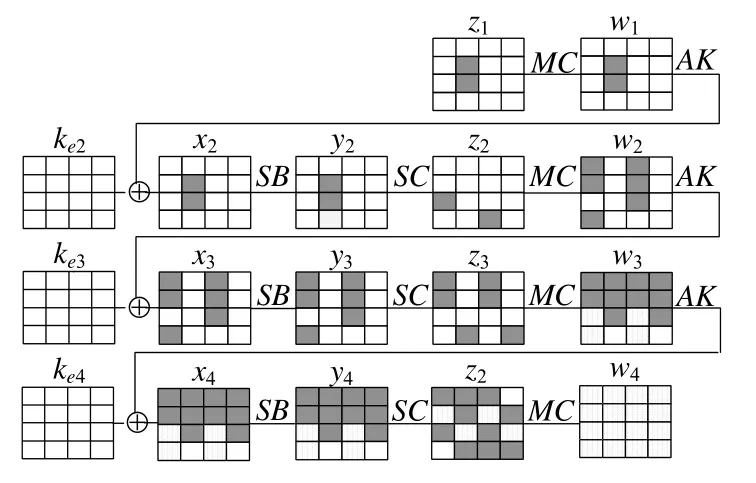
Fig.4 3.5-round differential path of Midori in encryption direction I圖4 3.5 輪Midori 算法加密方向差分路徑I

性質2.3.初始輸入狀態z1只在某一列存在3 個比特塊差分活動時,經過3.5 輪Midori 算法加密后,輸出狀態w4的每個比特塊都可能差分活動.

證明:z1經一輪Midori 算法加密后,輸出狀態z2必定只有1 個比特塊差分活動,由性質2.2 可知,z2再經2.5輪Midori 算法加密,輸出狀態w4的每個比特塊都可能存在差分活動.以z1僅在第5～第7 個比特塊差分活動為例,給出其3.5 輪Midori 算法加密過程,如圖5 所示. □

性質2.4.初始輸入狀態z1只在某一列存在4 個比特塊差分活動,經過3.5 輪Midori 算法加密后,輸出狀態w3的每個比特塊都可能差分活動.

證明:z1經一輪Midori 算法加密后,輸出狀態z2必定每一列各有一個比特塊差分活動.易知:再經1.5 輪算法加密,輸出狀態w3不存在確定有無差分活動的比特塊.以z1僅在第4～第7 個比特塊有差分活動為例,給出其3.5輪Midori 算法加密過程,如圖6 所示.□

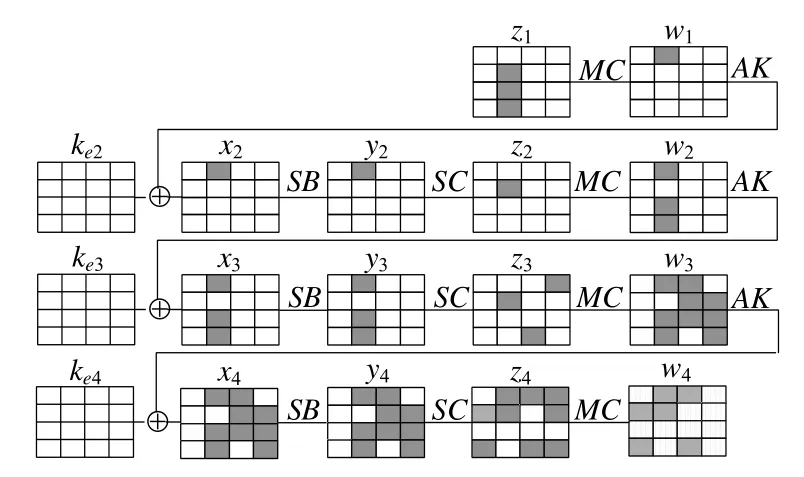
Fig.5 3.5-round differential path of Midori in encryption direction II圖5 3.5 輪Midori 算法加密方向差分路徑II

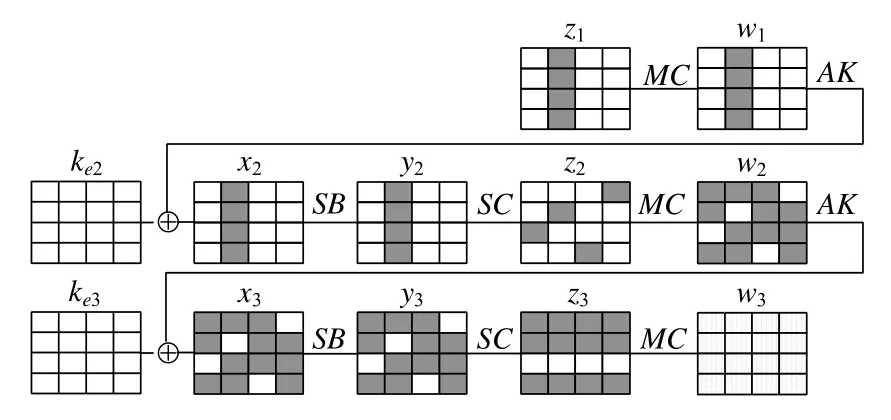
Fig.6 2.5-round differential path of Midori in encryption direction II圖6 2.5 輪Midori 算法加密方向差分路徑II

引理2.2.假設初始輸入狀態z1只在某一列存在比特塊差分活動時,若經過n+1/2 輪Midori 算法后,輸出狀態wn+1的每個比特塊都可能差分活動,則任意增加z1中其他差分為零列的差分活動得到狀態經過n+1/2輪Midori 算法后的輸出狀態也必定每個比特塊都可能差分活動.

證明:由SC,SB,KeyAdd,MC的性質可知,任意狀態,其列與列之間的這4 種變換是相互獨立的.故z1和經相同的變換,經變換后,輸出狀態有差分活動的比特塊集合必定包含z1的輸出狀態有差分活動的比特塊集合,所以該結論是顯然的. □

由引理2.1 和引理2.2 可得出如下定理.

定理2.1.任一初始輸入狀態z1經過3.5 輪Midori 算法加密后,輸出狀態w4的每個比特塊都可能差分活動.

2.2 Midori算法解密過程差分路徑

引理2.3.狀態zm只存在1 個比特塊差分活動時,經過3.5 輪Midori 解密算法后,輸出狀態xm?3的每個比特塊都可能差分活動.

證明:zm經一輪Midori 算法解密后,輸出狀態zm?1必定其中一列有3 個比特塊差分活動,其余列無差分活動比特塊.依據性質1.5,同理可證:再經過1.5 輪,輸出狀態xm?2必定其中3 列有兩個比特塊差分活動,一列有3 個比特塊差分活動.故xm?2再經一輪解密算法,輸出狀態xm?3每個比特塊都可能差分活動.以zm僅在第5 個比特塊有差分活動為例,給出其3.5 輪Midori 算法解密方向差分路徑,如圖7 所示.□

引理2.4.假設狀態zm只存在1 個比特塊差分活動時,若經過n+1/2 輪Midori 解密算法后,輸出狀態xm?n的每個比特塊都可能差分活動,則任意增加zm上其他比特塊的差分得到的狀態,經過n+1/2 輪Midori 解密算法后,輸出狀態每個比特塊也必定都可能差分活動.

證明:不妨將狀態上可能有差分活動的所有比特塊用集合H表示,例如zm上可能有差分活動的所有個比特塊集合用表示,狀態上可能有差分活動的所有個比特塊用集合表示,顯然有.由SC,SB,KeyAdd,MC的性質可知,.故zm和經相同的變換,經變換后輸出狀態有差分活動的比特塊集合,必定包含zm經變換后的輸出狀態有差分活動的比特塊集合,所以該結論是成立的.□

由引理2.3 和引理2.4 可得出如下定理.

定理2.2.任一狀態zn經過3.5 輪Midori 解密算法后,輸出狀態xn?3的每個比特塊都可能差分活動.

再由定理2.1 和定理2.2 可得出本文一個重要的結論,如定理2.3 所示.

定理2.3.Midori 算法在單密鑰條件下的截斷不可能差分區分器至多6 輪.

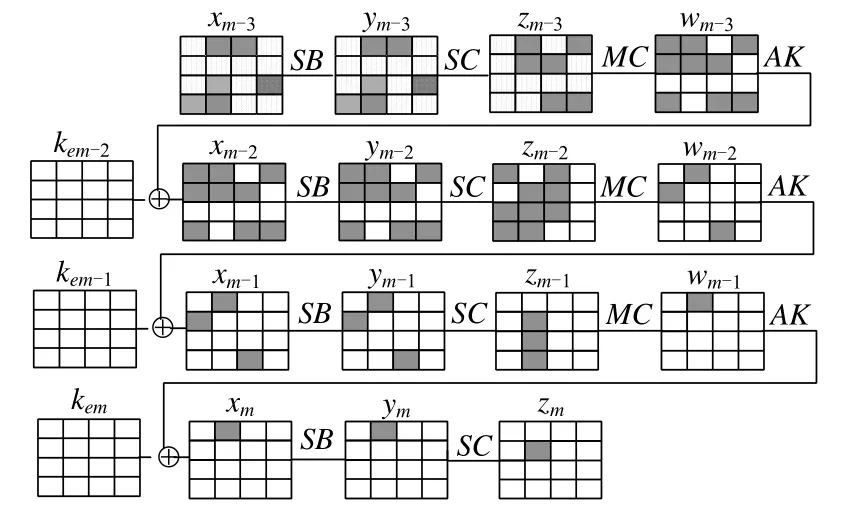
Fig.7 3.5-round differential path of Midori in decryption direction圖7 3.5 輪Midori 算法解密方向差分路徑

3 Midori 算法6 輪截斷不可能差分區分器的分類

在接下來分類過程中將用到一個概念——列最小差分活動比特塊數,其定義如下.

定義3.1.設狀態z各列的差分活動比特塊數分別為tcol(0),tcol(1),tcol(2),tcol(3),該狀態的列最小差分活動比特塊數,是指非零差分列中最小差分活動的比特塊數,即min{tcol(i)|tcol(i)>0,i=0,1,2,3}.

接下來,我們以輸入狀態z1的列最小差分活動比特塊數進行分類討論如下.

性質3.1.輸入狀態z1的列最小差分活動比特塊數為1 時,不可能構造出6 輪截斷不可能差分區分器.

證明:由性質2.1 和引理2.2 可知,此時,輸入狀態z1經過2.5 輪Midori 算法加密后,輸出狀態w3的每個比特塊都可能差分活動;再由定理2.2 可知,任意狀態經3.5 輪解密算法后,輸出狀態的每個比特塊都可能差分活動,故不可能構造出一條6 輪截斷不可能差分路徑.□

性質3.2.輸入狀態z1的列最小差分活動比特塊數為2 時,若要構造一條6 輪不可能差分路徑,輸出狀態z7必定僅有1 個比特塊差分活動.

證明:要想構造出一條不可能差分路徑,由性質2.2 可知,輸入狀態z1只能向下加密2.5 輪,所以輸出狀態z7要向上解密3.5 輪,且滿足存在確定有無差分活動的比特塊,故z7必定僅有1 個比特塊差分活動.□

性質3.3.輸入狀態z1的列最小差分活動比特塊數為3 時,要構造一條6 輪不可能差分路徑,若z1經過2.5輪Midori 算法加密,則輸出狀態z7必定僅有1 個比特塊差分活動.若輸入狀態z1經過3.5 輪Midori 算法加密,則z7經一次SC?1輸出狀態y7有如下4 種情形:(1)y7只有1 列有比特塊差分活動;(2)y7有兩列有比特塊差分活動,且其中一列差分活動比特塊數必定為1;(3)y7有3 列有比特塊差分活動,且其中兩列差分活動比特塊數必定為1;(4)y7每一列都有比特塊差分活動時,且必定有3 列其差分活動比特塊數為1.

證明:若輸入狀態z1經過2.5 輪Midori 算法加密,輸出狀態z7必定僅有1 個比特塊差分活動.若輸入狀態z1經過3.5 輪Midori 算法加密,則加密后輸出狀態w4的每個比特塊都可能存在差分活動,則z7必定滿足解密2.5輪后存在一定沒有差分活動的比特塊.對于輸出狀態z7經一次SC?1的輸出狀態y7分如下4 種情形討論.

· 情形1:當y7只有1 列有比特塊差分活動時,顯然是滿足要求的.

· 情形2:當y7僅有2 列有比特塊差分活動時,若這兩列都有兩個以上比特塊差分活動,容易推導出x5每個比特塊都可能存在差分活動,故不符合要求,所以此時y7必須有一列差分活動比特塊數為1.

· 情形3:當y7僅在3 列有比特塊差分活動時,若有兩列差分活動比特塊數超過一個,由情形2 可知不符合要求,所以y7其中兩列差分活動比特塊數必定為1.

· 情形4:當y7在每一列都有比特塊差分活動時,同樣由情形2 可知,有3 列差分活動比特塊數必定為1.綜上所述,性質3.3 得證.□

性質3.4.輸入狀態z1列最小差分活動半字節數為4 時,不可能構造出6 輪截斷不可能差分區分器.

該證明過程同性質3.1.

綜上所述,Midori 算法6 輪截斷不可能差分區分器可分為性質3.2 與性質3.3 兩大類.由引理2.2 和引理2.4可知,z1,z7僅有1 列有比特塊差分活動的情況下,區分器能向下加密及向上解密更多輪數.故簡單考慮z1,z7僅有1 列有比特塊差分活動的情況,此時按輸入狀態z1存在的差分活動比特塊數將Midori 算法6 輪截斷不可能差分區分器分為如下兩大類.

1) 輸入狀態z1僅在某一列存在2 個比特塊差分活動時,輸出狀態z7必定僅有1 個比特塊差分活動.具體不可能差分差分路徑為輸入狀態z1向下加密2.5 輪,輸出狀態z7向上解密3.5 輪.

2) 輸入狀態z1僅在某一列存在3 個比特塊差分活動時:(1) 若輸入狀態z1經過2.5 輪Midori 算法加密,則輸出狀態z7必定僅有1 個比特塊差分活動;(2) 若輸入狀態z1經過3.5 輪Midori 算法加密,則輸出狀態z7必定僅有1 個或者2 個比特塊差分活動(證明略).

4 Midori-64 算法的不可能差分分析

根據Midori 算法6 輪截斷不可能差分區分器的分類結果,可構造相應的6 輪不可能差分區分器.第4.1 節將給出一個6 輪不可能差分區分器;第4.2 節進一步給出Midori-64 算法的11 輪不可能差分分析.

4.1 Midori算法的6輪不可能差分區分器

定理4.1.當初始輸入狀態z1僅在第0～第2 這3 個比特塊差分活動,且滿足Δz1[0]=Δz1[1]=Δz1[2]時,經過6輪Midori 算法加密后,輸出狀態z7僅在第6、第7 比特塊處差分活動,且滿足Δz1[6]=Δz1[7]是不可能的.具體形式如圖8 所示.

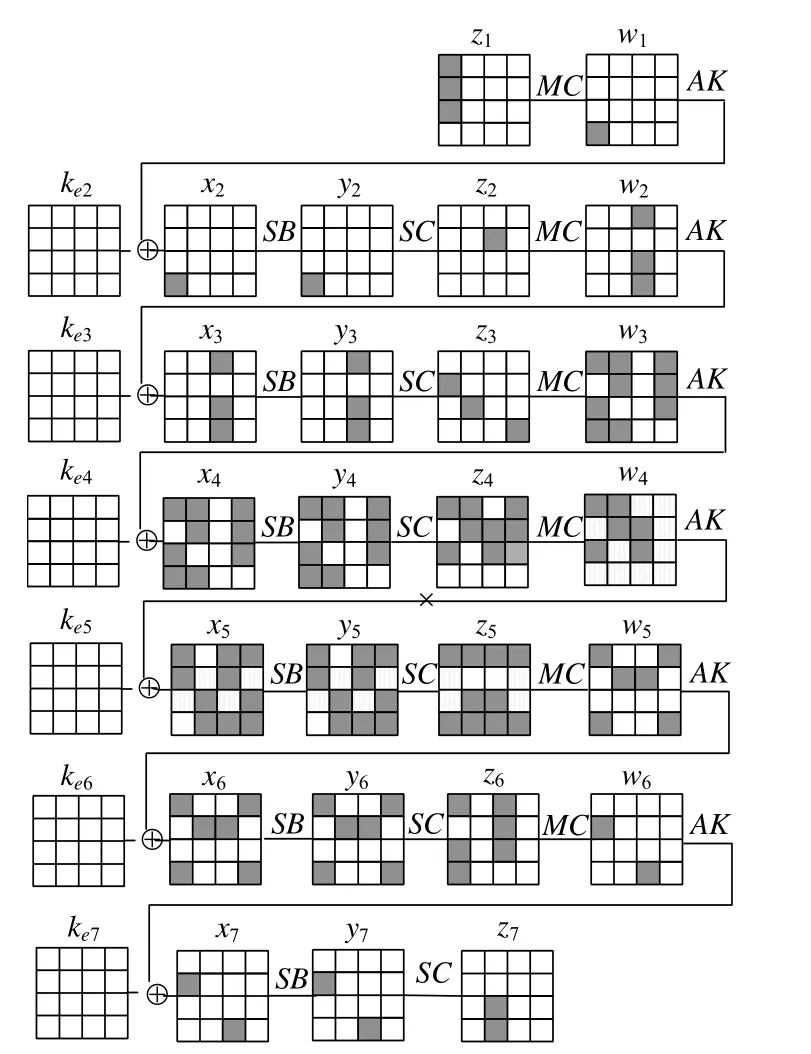
Fig.8 6-round impossible differential distinguisher of Midori圖8 Midori 算法的6 輪不可能差分區分器

證明:當輸入狀態z1僅在第0～第2 這3 個比特塊差分活動,且滿足Δz1[0]=Δz1[1]=Δz1[2]時,經3.5 輪Midori算法加密后,輸出狀態w4的第4 比特塊必定差分活動;當輸出狀態z7僅在第6、第7 比特塊處差分活動,且滿足Δz1[6]=Δz1[7]時,經2.5 輪Midori 算法解密后,輸出狀態x5的第4 比特塊差分為0,故產生矛盾,所以結論成立.證畢.□

4.2 11輪Midori-64算法的不可能差分分析

利用定理4.1 中給出的Midori 算法6 輪不可能差分區分器,向上解密1.5 輪,向下加密3.5 輪,給出11 輪Midori-64 算法的不可能差分分析結果.攻擊過程分為預計算與在線攻擊兩個階段.

(一) 在預計算階段,共需要預計算并存儲4 個表.

(二) 在線攻擊階段.

1.選擇2n個明文結構,其中的明文滿足在第1、第3、第5、第6、第9～第11、第14、第15 半字節上取所有的值,其余半字節取固定值.故一個明文結構包含236個明文,可以構造271個明文對.因此,攻擊的選擇明文量為2n+36,其中包含2n+71個明文對.

2.運用快速排序算法篩選明文對.篩選出密文在第4、第8 半字節差分不活動,在第1、第3、第5～第7、第9～第11、第13、第15 半字節差分活動的明文對,剩余2n+63個明文對.以明文對序號作索引,將篩選得到的明文對存儲在表Ω中,只需要存儲明文第1、第3、第5、第6、第9～第11、第14、第15半字節與密文第1～第3、第5～第7、第9～第15 半字節.

3.猜測出口白化密鑰ke11[0,1,2,3].對于表Ω中的2n+63個明文對,利用明文對序號可以得到其對應的密文差分ΔCcol(0).利用ΔCcol(0)查表T1,得到28個y10,col(0)和,可以確定密鑰ke11[0,1,2,3]=Ccol(0)⊕y10,col(0).以216個ke11[0,1,2,3]的可能值為索引,平均存儲2n+63×28/216=2n+55個明文對序號和在表Ω1中.

4.猜測出口白化密鑰ke11[5,6,7].已知ke11[0,1,2,3],對表Ω1中的2n+55個明文對,利用明文對序號可得其對應的密文差分ΔCcol(1).利用ΔCcol(1)查表T2,得到24個y10[5,6,7]和,可確定密鑰ke11[5,6,7].以ke11[5,6,7]為索引,平均存儲2n+55×24/212=2n+47個明文對序號和在表Ω2中.

5.猜測出口白化密鑰ke11[9,10,11].已知ke11[0,1,2,3,5,6,7],對于表Ω2中的2n+47個明文對,利用明文對序號可以得到其對應的密文差分ΔCcol(2).利用ΔCcol(2)查表T3,得到28個y10[9,10,11]和可以確定密鑰ke11[9,10,11];以ke11[9,10,11]為索引,平均存儲2n+47×24/212=2n+39個明文對和10,14,15])存儲在表Ω3中.

6.猜測出口白化密鑰ke11[12,13,14,15].已知ke11[0,1,2,3,5,6,7,9,10,11],對于表Ω3中的2n+39個明文對,可以得到其對應的密文差分ΔCcol(3).利用ΔCcol(3)查表T4,得到28個y10,col(3)和,可以確定密鑰ke11[12,13,14,15];以ke11[12,13,14,15]為索引,平均存儲2n+39×28/216=2n+31個明文對序號和13,14,15],存儲在表Ω4中.

9.已知ke11[0,1,2,3,5,6,7,9,10,11,12,13,14,15]與取值,根據密鑰擴展算法,由出口白化密鑰ke11[0,1,2,3,5,6,7,9,10,11,12,13,14,15]可以直接得到入口白化密鑰ke0[1,3,5,6,9,10,11,14,15],利用上述密鑰對Ω6中2n+11個明文對加密1 輪,篩選出滿足使得僅在Δw0[0,5,10]處活動的明文對.以為索引,表Ω7中存儲2n+11×2?24=2n?13個明文對序號.

10.已知密鑰ke11[0,1,2,3,5,6,7,9,10,11,12,13,14,15]與取值,窮舉212個密鑰ke1[0,5,15].利用上述密鑰對Ω7中2n?13個明文對加密1/2 輪,以2?8的概率得到不可能差分區分器的輸入.將通過檢測的密鑰列為候選密鑰,最后對候選密鑰窮舉10 個半字節密鑰及ke11[4,8],進行11 輪Midori 算法加密檢測得到的128 比特密鑰是否正確.具體的攻擊路徑如圖9 所示,其中,網狀表示猜解的密鑰半字節.

Fig.9 11-round impossible differential cryptanalysis of Midori-64圖9 11 輪Midori-64 算法不可能差分分析

由定理4.2 給出上述11 輪Midori-64 算法不可能差分分析的復雜度分析結果.

定理4.2.利用6 輪不可能差分區分器對11 輪Midori-64 算法進行不可能差分分析,恢復128 比特主密鑰,其時間復雜度為2121.4次11 輪Midori-64 算法加密,數據復雜度為260.8個選擇明文,存儲復雜度為296.5個Midori-64 狀態.

證明:下面給出11 輪Midori-64 算法不可能差分分析中步驟1～步驟9 各步驟的復雜度,見表3.證畢.□

Table 3 Complexity of 11-round impossible differential cryptanalysis on Midori-64表3 11 輪Midori-64 算法不可能差分分析復雜度

由表3 可知,前9 個分析步驟,其時間復雜度大約為2n+96.6次11 輪Midori-64 算法加密.對于第10 步,在88比特已知密鑰下,對2n?13個明文對加密0.5 輪的時間復雜度為288×212×2n?13×0.5×2/11≈2n+83.5次11 輪Midori-64算法加密;經過檢測后候選密鑰集規模,對剩余40 比特密鑰進行窮舉恢復主密鑰的時間復雜度為ε×240.當n=24.8 時,11 輪Midori-64 算法不可能差分分析總時間復雜度為296.6+24.8+283.5+24.8+2100×次11 輪Midori-64 算法加密,數據復雜度為260.8個選擇明文,存儲復雜度約為295.8×(4+87.8/4)/16≈295.5個Midori-64 狀態.

5 結 論

本文證明了在單密鑰條件下Midori 算法的截斷不可能差分區分器至多6 輪,并對6 輪截斷不可能差分區分器進行分類;其次,根據Midori 算法6 輪截斷不可能差分區分器的分類構造了一個較優的6 輪區分器,并給出了11 輪Midori-64 算法的不可能差分分析,其時間復雜度為2121.4,數據復雜度為260.8,存儲復雜度為296.5.該結果表明,本文給出了一個較好的11 輪Midori-64 算法的分析.對于Midori-128 算法是否也可以根據Midori 算法6輪截斷不可能差分區分器的分類構造出較優的區分器,以得到較好的不可能差分分析結果,這是我們下一步要考慮的問題.

作者注 本文是我們于2018 年4 月24 日投到《軟件學報》的論文.該文是戰略支援部隊信息工程大學郭建勝老師(本文第二作者)指導的2018 屆(2018 年12 月)畢業的研究生李明明(本文第一作者)的碩士學位論文《典型輕量級分組密碼算法不可能差分分析研究》工作成果的一部分,特此說明.