丘陵山地拖拉機車身調平雙閉環模糊PID控制方法

齊文超 李彥明 張錦輝 覃程錦 劉成良 殷月朋

(1.上海交通大學機械與動力工程學院， 上海 200240； 2.山東五征集團， 日照 276800)

0 引言

丘陵山區耕地面積約占我國總耕地面積的63.2%，其糧油產量超過總產量的50%，在我國農業生產中具有不可替代的重要地位。丘陵山區作業環境多為傾斜角度較大的斜坡，傳統農機裝備在丘陵山區作業時效率低、乘坐舒適性差，甚至會出現側傾、翻車等嚴重的安全事故。因此，亟待研發具備自動調平功能的丘陵山地拖拉機，同時提高其自動調平控制性能[1-4]。

國外對丘陵山地調平系統的研究起步較早，XIE等[5]、HOEHN等[6]研發的調平系統專用于坡地作業聯合收獲機。LEONARD等[7]研發的自動調平系統應用于靜止狀態的車輛調平，不能在行駛中調平；PIJUAN等[8]設計的可調節高度懸掛機構具有較強陡坡越障能力，并不需要嚴格控制調平精度。國內在果園升降平臺調平[9-12]、農機具調平控制系統[13-16]、高空升降平臺調平控制[17-19]方面研究較多，關于丘陵山地拖拉機自動調平控制研究相對較少。文獻[20-22]提出了一種基于PID控制算法的自動調平系統，應用于履帶式拖拉機。彭賀等[23-24]研制了基于液壓缸驅動的車身四點調平機構，對其進行了詳細的運動學和動力學仿真分析，在此基礎上設計了一套車身自調平控制系統，最后在自調平試驗臺上開展了相關試驗驗證。上述研究為丘陵山地拖拉機車身自動調平控制方法設計與改進提供了重要的依據。

為提高丘陵山地拖拉機作業安全性和作業效率，本文在由液壓馬達驅動的丘陵山地拖拉機姿態調整機構的基礎上，設計基于雙閉環模糊PID算法的自動調平控制方法，以實現車身自動調平并提高其控制精度。并與雙閉環PID算法進行對比，通過仿真與試驗驗證所設計的自動調平雙閉環模糊PID控制方法性能及對起伏較大坡地等惡劣作業環境的適應性。

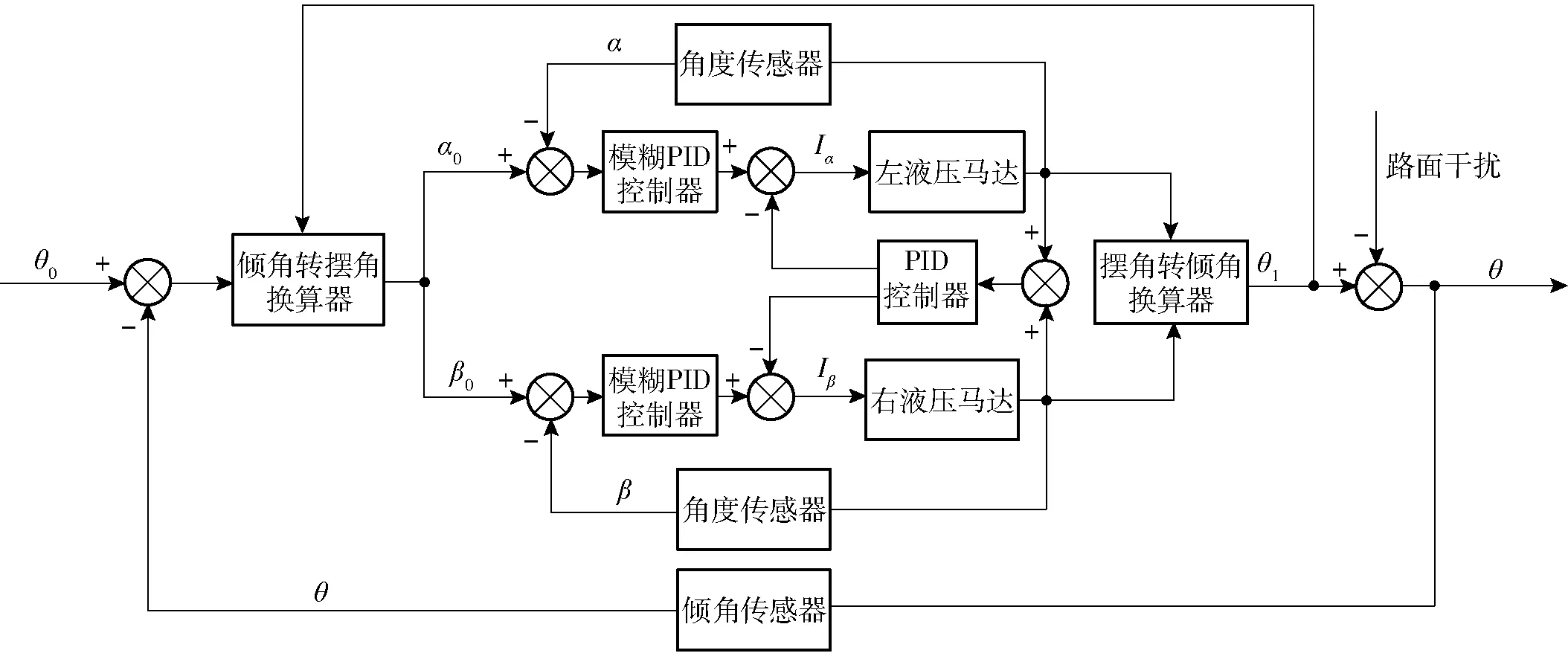
圖2 自動調平系統控制框圖Fig.2 Automatic leveling system control block diagram

1 自動調平控制原理

丘陵山地拖拉機前驅動橋為隨動系統，姿態調整機構安裝于后驅動橋上。如圖1a所示，A、B兩點的連線與水平線間的夾角為車身橫向傾角。該丘陵山地拖拉機所使用的姿態調整機構，是通過左右兩擺動機構擺動所產生的高度差與路面傾角抵消來實現車身橫向調平，左右擺動機構分別由兩個液壓馬達驅動。如圖1b所示，左右擺動機構擺動范圍為±80°。液壓馬達的轉速與轉動方向分別由兩個電液比例閥控制。因此，通過調節電液比例閥開口大小及方向可控制擺動機構的擺動速度和擺動方向，從而實現車身調平。為保證車輛正常行駛，需保證左右擺動機構擺動角度相等、方向相反。

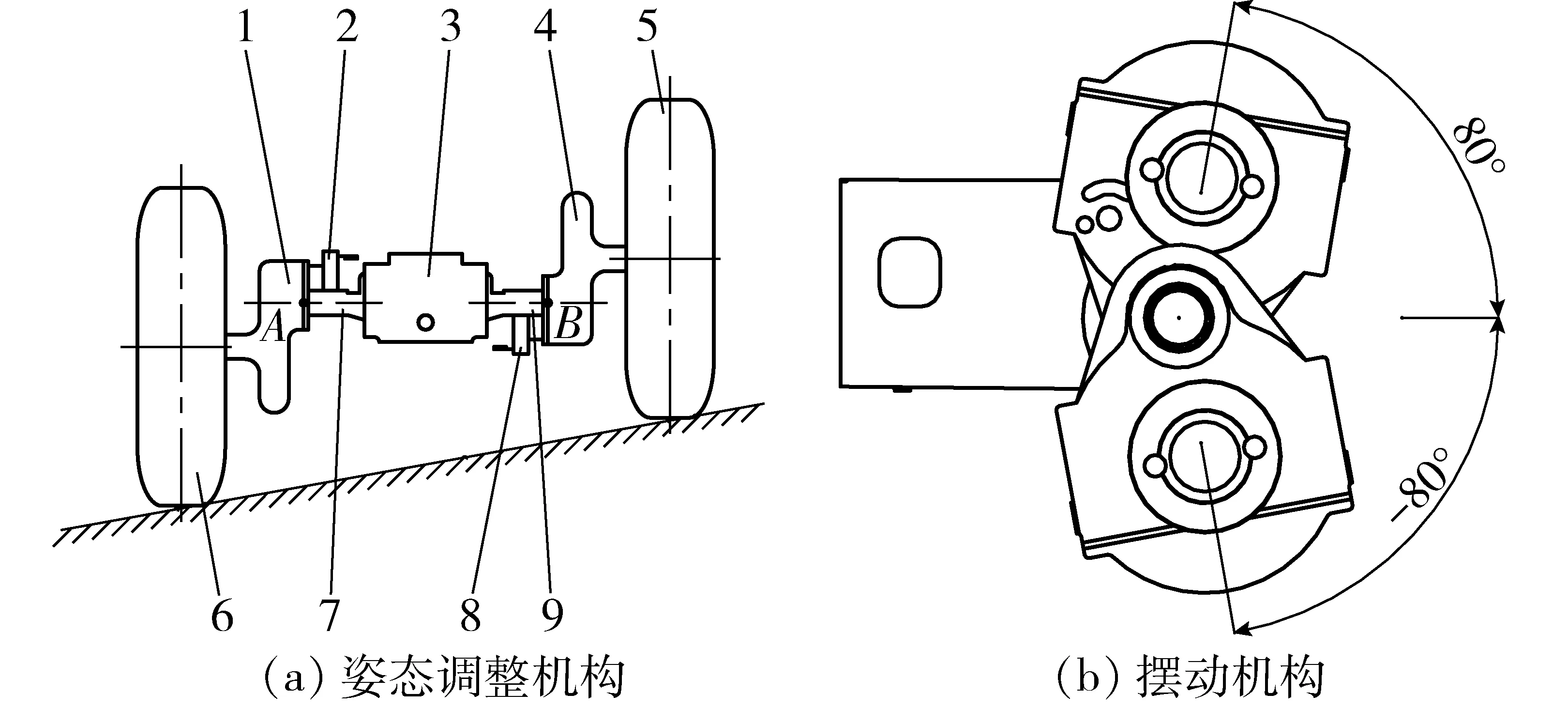
圖1 姿態調整機構示意圖Fig.1 Attitude adjustment mechanism diagrams1.左末端傳動機構 2.左擺動機構 3.后驅動橋 4.右末端傳動機構 5.右車輪 6.左車輪 7.左半軸套管 8.右擺動機構 9.右半軸套管

為實現自動調平，在左右兩擺動機構上各安裝有角度傳感器測量擺動機構擺動角，在車身上安裝傾角傳感器測量車身橫向傾角。主控器根據上述傳感器實時接收的數據進行處理分析，輸出相應大小的電流控制兩個比例電磁閥開口方向及大小，從而調整液壓馬達轉速和轉向，使左右擺動機構擺動，實現車身的自動調平，如圖2所示(圖中θ0、θ分別為車身目標傾角和傾角傳感器檢測的實際傾角；α0、α、Iα分別為左擺動機構目標擺角、角度傳感器檢測的實際擺角和左比例閥輸入電流；β0、β、Iβ分別為右擺動機構目標擺角、角度傳感器檢測的實際擺角和右比例閥輸入電流；θ1為車身本身傾角)。基于雙閉環模糊PID算法的自動調平控制系統工作原理為：主控器實時接受傾角傳感器、兩角度傳感器所檢測到的車身橫向傾角和左右兩擺動機構擺角，通過傾角轉擺角換算器計算出左右兩擺動機構應擺動角度。外環采用模糊PID控制使兩擺動機構擺動到目標角度，內環采用PID控制保證擺動過程中左右兩擺動機構擺動角度相等、方向相反。

其中，傾角轉擺角換算器和擺角轉傾角換算器計算公式為

Ltan(θ0-θ+θ1)=lsinα0-lsinβ0

(1)

lsinα-lsinβ=Ltanθ1

(2)

其中

α0=-β0

式中L——輪距，m

l——擺動機構擺動半徑，m

2 系統建模

2.1 閥控馬達系統狀態空間模型

被控對象為比例閥控馬達系統，故建立該閥控馬達系統狀態空間模型。液壓馬達負載流量方程為

QL=Kqxv-KcpL

(3)

式中Kq——流量增益系數

xv——閥芯開口位移，m

Kc——流量壓力系數，m5/(N·s)

pL——負載壓差，Pa

電液比例閥的傳遞函數為比例環節

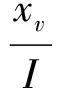
(4)

式中I——通入比例電磁鐵電流，A

Ksv——比例系數

液壓馬達流量連續性方程為

(5)

式中Dm——液壓馬達理論排量，m3/rad

θm——液壓馬達轉角，rad

Ctm——液壓馬達泄漏系數，m5/(N·s)

Vt——閥腔、馬達腔與連接管道總容積，m3

βe——油液有效體積彈性模量，Pa

當液壓馬達與負載力平衡時，滿足方程

(6)

式中Jt——液壓馬達和負載折算到馬達軸上的總慣量，kg·m2

Bm——液壓馬達和負載的粘性阻尼系數

G——負載的扭轉彈簧剛度，N/m

TL——作用在馬達軸上的負載力矩，N·m

以液壓馬達轉角x1、馬達角速度x2和負載壓差x3為系統的狀態變量，比例電磁閥輸入電流u1和作用在馬達上的負載力矩u2為系統輸入，液壓馬達轉角y為系統輸出，令

(7)

由式(3)～(6)得閥控馬達系統狀態空間模型

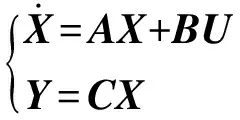
(8)

其中

(9)

(10)

C=[1 0 0]T

(11)

(12)

式中A——系統矩陣

B——輸入矩陣

C——輸出矩陣

Kce——總流量壓力系數，m5/(N·s)

ωh——液壓固有頻率，rad/s

ζh——液壓阻尼比

2.2 模糊PID 控制器

2.2.1控制算法

傳統PID控制算法為

(13)

式中u(t)——控制器輸出量

e(t)——控制器輸入量

kp——比例增益

ki——積分增益

kd——微分增益

由于丘陵山地拖拉機電液系統是一種典型的非線性不確定性系統，傳統PID控制算法參數均為定值，難以充分發揮PID控制器的優良控制作用。故利用模糊控制進行改進，如圖3所示，擺動機構擺角誤差e及其變化率ec模糊化后根據模糊控制規則進行決策，模糊控制器使用面積中心法解模糊后得到PID參數在線調整量Δkp、Δki和Δkd，與PID參數初始值相加，實現PID參數在線自整定，即

(14)

式中kp0、ki0、kd0——PID參數初始值

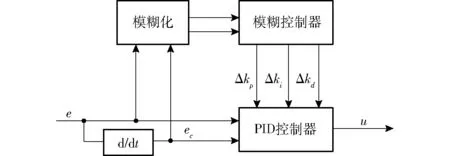
圖3 模糊PID控制框圖Fig.3 Fuzzy PID control block diagram

2.2.2模糊控制器設計

擺動機構擺角誤差e及其變化率ec基本論域分別為[-1.4，1.4]和[-0.1，0.1]；修正參數Δkp、Δki和Δkd的基本論域分別為[-0.6，0.6]、[-0.05，0.05]和[-0.1，0.1]。設定輸入輸出對應論域皆為[-6，6]，模糊子集為{NL，NM，NS，ZO，PS，PM，PL},分別表示負大、負中、負小、零、正小、正中、正大。因此e及其變化率ec的量化因子分別為Ke=4.29，Kec=60；Δkp、Δki和Δkd的量化因子分別為KΔkp=10，KΔki=120，KΔkd=60。隸屬度函數采用三角形函數。模糊規則設計原則如下：

(1)當擺角誤差e較大，應適當增大比例增益kp從而提高擺動速度，適當減小積分增益ki以抑制積分項影響，同時減小微分增益kd避免瞬時微分過分飽和。

(2)當實際擺角與目標擺角較為接近，即誤差e及其變化率ec均為中間值時，取適中的kp防止超調，并取適中的ki和kd保證系統響應速度。

(3)當實際擺角基本達到目標擺角并趨于穩定時，應適當增大積分增益ki以減小系統穩態誤差，當ec較小時適當增大kd，ec較大時適當減小kd，從而減小系統振蕩。

根據上述設計原則，并結合工程經驗指定kp、ki、kd的模糊規則，如表1所示(以kp為例)。

3 仿真分析

使用Matlab分別建立基于雙閉環PID算法和雙閉環模糊PID算法的丘陵山地拖拉機自動調平控制系統模型。丘陵山地拖拉機實際行駛過程中，作用在液壓馬達軸上的負載力矩是不斷變化的，為簡化數值分析過程，假設作用在液壓馬達軸上的負載力矩為恒定值。為對比兩種方法的控制性能，使用相同的PID參數進行仿真。系統模型參數如表2所示。

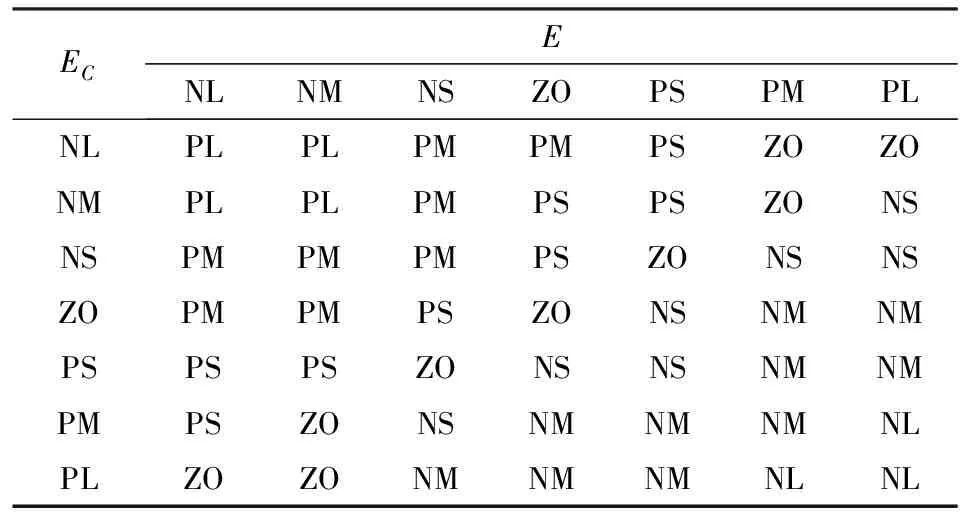
表1 kp模糊控制規則Tab.1 Fuzzy control rule of kp

注：E、EC分別為e、ec的語言變量。

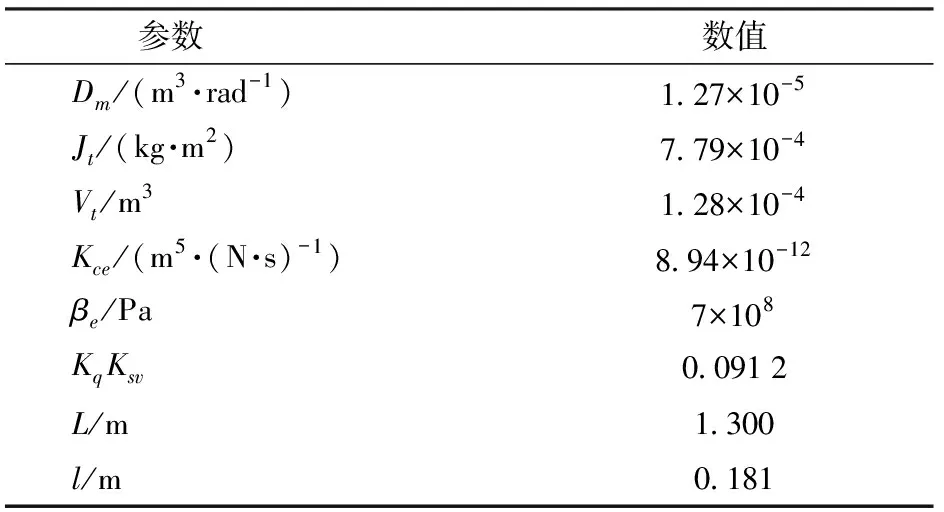
表2 系統模型參數Tab.2 Parameters of system model

3.1 擺動機構控制性能

姿態調整機構極限擺動角為80°，故75°為安全擺動角度。給定幅值為75°擺角的階躍信號。

仿真結果如圖4所示，tr為上升時間，tp為峰值時間，ts為調節時間，Mp為最大超調量。圖4a為PID控制下的仿真結果，由圖可知，上升時間為11.5 s，最大超調量約為1.5°。圖4b為模糊PID控制下的仿真結果，由圖可知，調節時間為10.5 s，且擺動角度基本無超調。可見，使用模糊PID控制擺動機構可以減小超調量并增加擺動速度。

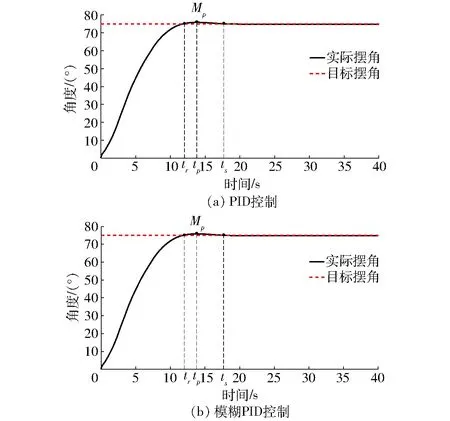
圖4 擺動目標為75°時仿真結果Fig.4 Simulation results of swing target at 75°

3.2 自動調平控制性能

丘陵山地地區作業環境多為15°以內的較平穩的斜坡，根據擺動機構設計尺寸可知，當左右擺動機構擺角分別達到75°和-75°時，車身可達到15°傾角。因此給定幅值為15°路面傾角的階躍信號。由圖5可知，使用雙閉環模糊PID控制方法較雙閉環PID控制具有增加調平速度和減小超調量的優點。

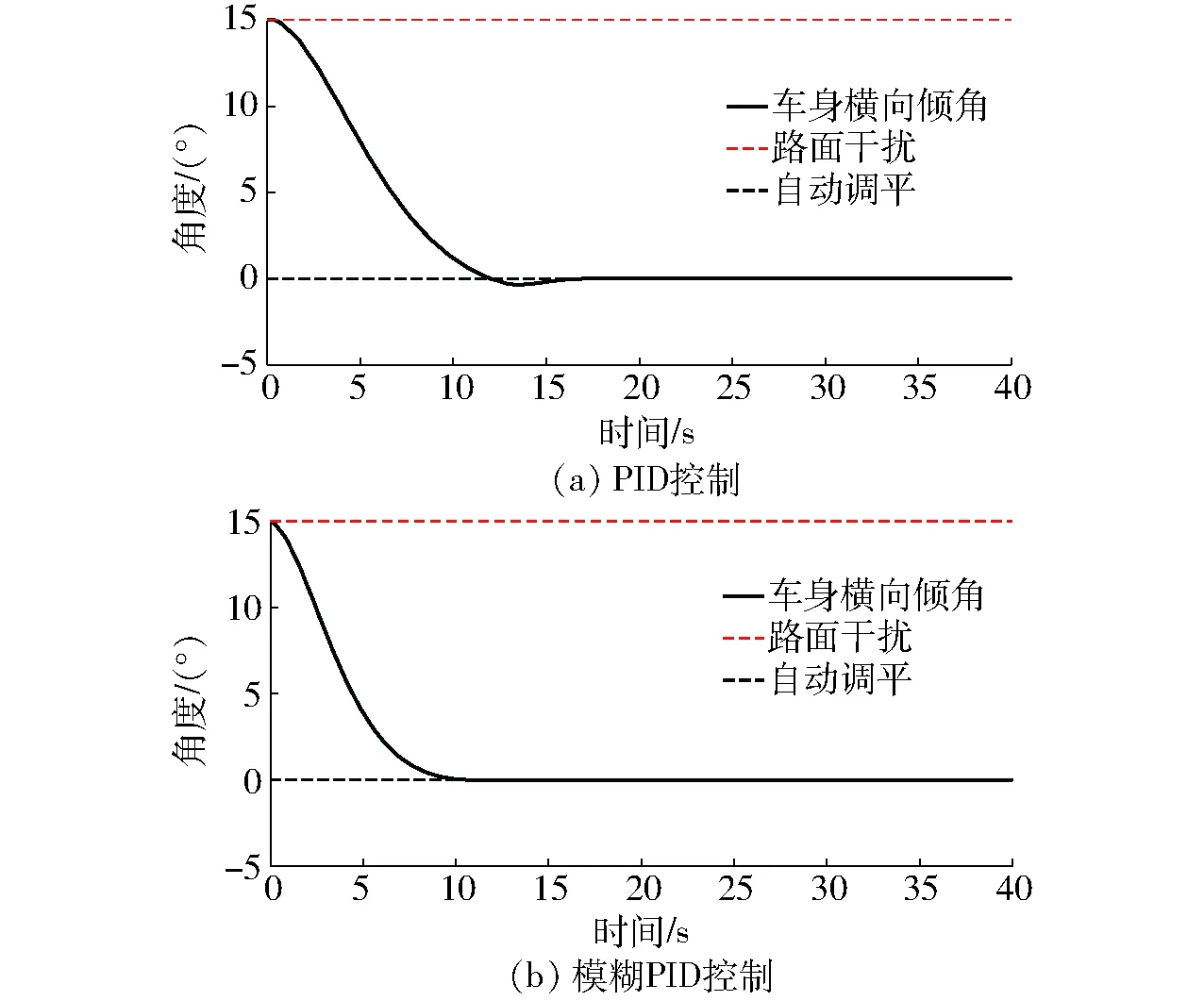
圖5 15°坡地自動調平仿真結果Fig.5 Simulation results of 15°slope leveling

4 試驗與分析

4.1 試驗設備與條件

對山東五征集團生產的拖拉機進行改裝，安裝已研制的姿態調整機構，并安裝主控器、傳感器等控制元件。使用自主研發的主控器，該主控器使用STM32F407ZGT6作為CPU，內部集成英飛凌公司生產的TLE82453-3SA芯片，可編程輸出PWM電流范圍為0～1.5 A，分辨率為0.73 mA，用于控制比例電磁閥。主控器集成CAN總線通訊接口，用于實時接收安裝于車身及擺動機構上的傳感器數據。使用3個北微公司生產的BW-VG525型超精度動態傾角傳感器，動態精度為0.3°，分別安裝于車身和兩擺動機構上，用來測量車身橫向傾角和擺動機構擺角。試驗拖拉機如圖6所示。

圖6 試驗拖拉機實物圖Fig.6 Experiment tractor physical map

4.2 試驗內容及結果

4.2.1靜態試驗

圖7 靜態試驗現場Fig.7 Static experiment site

如圖7所示，拖拉機擺動機構初始擺角均為0°，靜止在15°的斜坡上，啟動自動調平程序。分別使用雙閉環PID算法和雙閉環模糊PID算法進行試驗，試驗結果如圖8所示。

圖8a、8c分別為雙閉環PID控制下，擺動機構擺動狀況和車身調平狀況；圖8b、8d分別為雙閉環模糊PID控制下，擺動機構擺動狀況和車身調平狀況。對比可發現：雙閉環模糊PID控制較雙閉環PID控制，調平過程基本無超調，且調平時間較短，與仿真結果相符。調平時間約為12.5 s，最大調平誤差小于0.5°，且無超調現象，左右兩后輪擺角絕對值差在±1°以內，滿足丘陵山地正常作業需求。

4.2.2動態試驗

如圖9所示，拖拉機分別使用雙閉環PID算法和雙閉環模糊PID算法啟動自動調平程序，以1擋速度(1.98 km/h)行駛在高低起伏較大的坡地上，模擬惡劣工況。

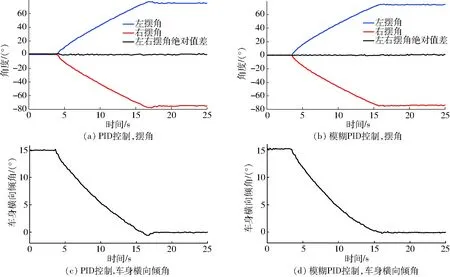
圖8 靜態試驗結果Fig.8 Static experimental results

圖9 動態試驗現場Fig.9 Dynamic experimental site

首先，拖拉機不啟動自動調平程序，行駛于該路面上，得到實測路面傾角如圖10所示。由圖可知，最大傾角約為14°，地面高低起伏較大，可模擬惡劣作業環境。

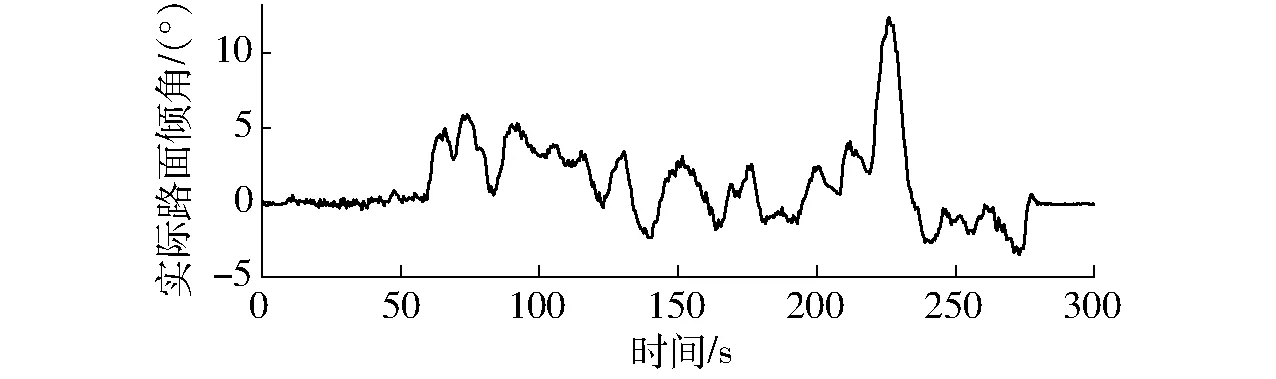
圖10 實際路面傾角變化曲線Fig.10 Changing curve of measured tilt angle

啟動自動調平程序后，試驗結果如圖11所示。圖11a為基于雙閉環PID算法和雙閉環模糊PID算法的自動調平控制方法下車身調平狀況。經計算可得，雙閉環PID控制下，車身橫向傾角最大誤差為4.325 0°，平均絕對誤差為0.713 3°，均方根誤差為1.052 7°；雙閉環模糊PID控制下，車身橫向傾角最大誤差為2.870 0°，平均絕對誤差為0.499 5°，均方根誤差為0.755 7°。可見，在雙閉環模糊PID控制下，車身橫向傾角最大誤差、平均絕對誤差和均方根誤差均有所減小，提高了調平控制精度。

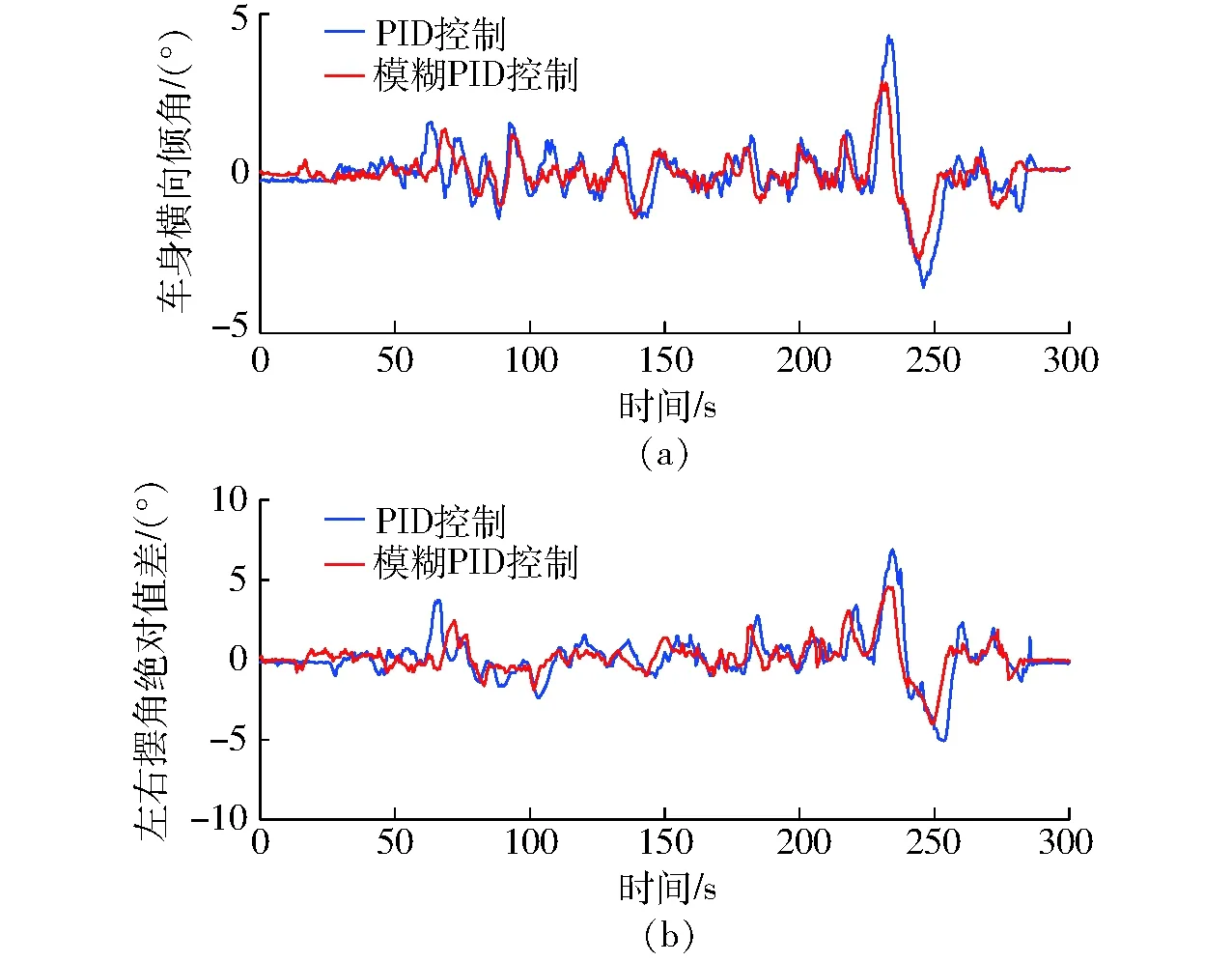
圖11 動態試驗結果Fig.11 Dynamic experimental results

圖11b為基于雙閉環PID算法和雙閉環模糊PID算法的自動調平控制方法下擺動機構擺動狀況。經計算可得，雙閉環PID控制下，左右擺動機構擺角絕對值差最大誤差為6.890 0°，平均絕對誤差為1.118 7°，均方根誤差為1.689 1°；雙閉環模糊PID控制下，左右擺動機構擺角絕對值差最大誤差為4.550 0°，平均絕對誤差為0.814 7°，均方根誤差為1.204 1°。

經對比可知，在惡劣作業環境下，雙閉環模糊PID控制效果優于雙閉環PID控制。在高低起伏較大(最大傾角小于15°)的坡地上，車身傾斜角度可控制在±3°范圍內，左右車輪擺角絕對值差在±5°范圍內，能夠滿足車輛正常行駛和作業需求。拖拉機啟動自動調平控制程序后，在0～60 s以及280 s之后在兩段平穩路面上行駛期間，車身橫向傾角及其左右擺動機構擺角絕對值差基本為0°，因此穩態誤差為0°。

5 結論

(1)提出了一種基于雙閉環模糊PID控制算法的丘陵山地拖拉機自動調平控制方法。運用Matlab對系統進行數值分析，表明利用雙閉環模糊PID控制算法相比于雙閉環PID算法可減小超調，提高調平速度，并驗證了該自動調平控制方法能有效滿足車身橫向調平需求。

(2)對整機進行試驗驗證，結果表明，所提出的控制方法性能優于雙閉環PID算法，在±15°的坡地上調平時間為12.5 s，調平誤差小于0.5°，左右兩后輪擺動機構的擺角絕對值差在±1°以內，且無超調現象。

(3)以1.98 km/h的速度行駛在高低起伏的惡劣工作環境下，車身傾斜角度可控制在±3°范圍內，左右擺動機構擺角絕對值差在±5°范圍內。可見，所設計的基于雙閉環模糊PID控制算法的自動調平控制方法使丘陵山地拖拉機不僅能在較平緩的丘陵坡地上安全作業，并能適應起伏較大坡地等惡劣作業環境，相比于雙閉環PID控制性能更優。