基于改進關聯規則的卸船機故障預測模型

葉永偉 程毅飛 賴劍人 任設東

浙江工業大學特種設備制造與先進加工技術教育部/浙江省重點實驗室，杭州，310014

0 引言

橋式抓斗卸船機是企業港口生產中重要的大型散料卸貨工具，具有抓斗起升和開閉、小車行走、前大梁仰俯及整機沿軌道行走的功能，在實際生產中占有很重要的地位。卸船機發生故障會影響到原有功能，有可能出現嚴重的事故，造成經濟損失[1],因此有必要對卸船機系統的健康狀態進行監測、故障分析和故障預測，以確保卸船機安全穩定地運行，提早預警，減少因突發故障產生的經濟損失以及避免人員傷亡等重大事故的發生[2]。

故障趨勢預測方法作為短時預測方法，主要包括基于機理模型和基于數據驅動的故障預測方法[3-4]。近年來，隨著傳感器技術和信息處理技術的發展，基于數據驅動的方法由于僅需利用設備運行狀態的監測數據就能及時地反映出設備的性能狀態，實現故障預測而被廣泛應用。傳統方法中，基于數據驅動的港口船機故障診斷方法主要有：神經網絡故障診斷方法模擬船機復雜的非線性系統，以故障特征信號作為神經網絡輸入，診斷結果作為網絡輸出；專家系統故障診斷方法通過求解船機復雜的實際問題，推斷船機故障所在；小波分析方法利用信號變換特征進行故障識別；故障樹診斷方法尋找船機的故障致因；粗糙集理論用于挖掘船機中隱含的知識，揭示潛在的規律；多傳感器信息融合診斷技術獲取船機各種特征參數信息，建立船機故障的預測、定位和排除模型等[5-6]。其中，基于多傳感器信息融合故障預測模型主要根據設備正常工作與異常工作狀態提取分析各種特征參數的變化信息來實現設備故障的預測過程。如橋式抓斗卸船機這種工作環境比較惡劣，易受到載荷、工況變化等不確定因素影響的設備，其運行過程狀態呈現出動態的、實時變化的特征。因此采用關聯規則分析方法獲得表征卸船機狀態的關聯規則，并利用改進的多傳感器信息融合故障預測方法能夠準確地實現卸船機實時運作下的故障預測。

楊行舟等[7]研究了基于徑向基函數神經網絡的門式起重機故障診斷系統。崔英等[8]提出了融合遠程監控、專家系統、智能診斷功能要求于一體的起重機遠程監控及故障診斷系統。裴瑋等[9]提出基于分布式光纖傳感技術的動態數據時間序列分析模型，對起重機主梁進行損傷預警。呂金華等[10]采用小波包分解和神經網絡相結合的方法對卸船機電機進行故障診斷。尚敬強等[11]將遺傳算法與人工神經網絡結合，并應用于起重機狀態識別和故障診斷。舒安慶等[12]建立了故障樹診斷分析門座式起重機臂架折斷的主要風險源。田海雷等[13]建立了小波包分解和支持向量機相結合的預測模型，對液壓泵進行故障預測。SAFIZADEH等[14]利用多傳感器數據融合技術對滾動體振動故障進行了診斷研究。目前卸船機真實故障表現為多個故障特征信號相互耦合，僅對單一故障進行診斷不能根治整機系統故障隱患，應該深入研究系統內部各組成部分的相互作用和聯結關系。橋式抓斗卸船機實際狀態監測參量之間存在復雜的相關性，傳統線性相關性處理方式并不適用于卸船機的實際工況。

本文采用興趣度關聯規則來表征卸船機的運行狀況，引入權重系數來定量分析其狀態特征變化，并將其應用到橋式抓斗卸船機故障預測中[15]。首先，利用改進的關聯規則算法挖掘監測數據，獲取表征卸船機狀態的關聯規則；然后計算故障類型與故障征兆、故障征兆與關聯規則兩兩之間的關聯關系，并確定其權重系數，構建卸船機預測模型；最后，通過實時監測關聯規則組的狀態變化，進行卸船機的狀態評估和故障預測。

1 興趣度關聯規則理論

傳統Apriori算法下的支持度-置信度框架體系，只能適應于離散型數據的關聯規則挖掘，同時基于此框架的關聯規則采掘存在許多弊端[16]，文獻[16]指出支持度閾值設定得過低或過高將會導致產生價值冗余的規則或丟失有用的規則，因此要避免將支持度作為最初項集產生的主要決定因素[17]。針對橋式抓斗卸船機監測數據特征，先將其進行聚類離散化處理，并用興趣度I來反映關聯規則中A和B的關系程度，用置信度C來反映這種情況的發生方向，用支持度S來反映這種情況是否為普遍規律。

1.1 興趣度關聯規則描述

關聯規則(association rules, AR)表示數據庫中隱含于若干項目之間且滿足某種設定要求的關聯關系的規則，可以定義為形如A?B(A稱為規則的左側，B稱為規則的右側)的蘊含式，其中A?T，B?T，A∩B=?，T為事務數據庫D中的事務項[18]。在關聯規則中,記：

(1)數據庫中所有事務項T的個數為|D|；

(2)T中項集A出現頻率為f(A)；

(3)A?B的支持度是D中包含A∪B的比例，用概率來表示，supp( )表示支持度，即

(1)

(4)A?B的置信度是D中包含A的同時又包含B的比例，用條件概率來表示，conf( )表示置信度，即

(2)

(5)S(A?B)min為關聯規則的最小支持度，C(A?B)min為關聯規則的最小置信度。

興趣度是指基于統計獨立性假設下真正的強度與期望的強度之比，給定交易集D上基于概率論的關聯規則A?B的興趣度[19]：

(3)

其中，值域為Mi，當I值遠大于1時,表明這條規則越感興趣，實際利用價值越大；當I值遠小于1時，表明該規則的反面規則越感興趣；I不小于0。

1.2 Apriori算法改進

Apriori算法不能直接用于工程領域數據庫中屬性為數值型(如應力)的狀態參數，以及各運行設備和系統機械狀態之間關聯程度未知的情況，需先將其轉化為布爾型關聯規則進行挖掘[20]。根據橋式抓斗卸船機本身的關聯特性和其生產規律以解決Apripri的適應性問題，本文將改進算法分為以下三部分。

(1)利用聚類算法將數據離散為布爾型。引入聚類算法離散，達到兩方面目的：①分層聚類。考慮到橋式抓斗卸船機監測狀態參數屬于實時采集，數值型屬性主要為振動烈度和應力值，故將數值型數據進行分區處理，轉化為布爾型關聯規則進行處理。②劃分聚類。根據卸船機實際運行狀態，保存數量較小的類，得到數據的實際分布結果[21]。

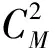
(3)引入興趣度提高規則質量。利用興趣度描述A和B之間的關系密切程度，避免支持度和置信度體系帶來的局限性，排除支持度閾值過低和過高所引起的規則冗余、規則缺失等情況。在興趣度-支持度-置信度框架運行過程中根據以下4種情況來篩選滿意的關聯規則(Cmin代表最小置信度，Imin代表最小興趣度)：①CCmin，|I|Cmin，I>Imin，表明該規則有較高的實際利用價值，輸出；④C>Cmin，-I>Imin，表明該規則的反面規則有比較高的實際利用價值，輸出。

根據卸船機實際運行監測狀態信息，排除情況④中反面規則的出現。

(4)改進的Apriori算法流程如圖1所示。圖中，mCA表示用于數據聚類的競爭聚類算法；L1表示1-頻繁項集，K表示循環次數，LK表示K-候選項集。

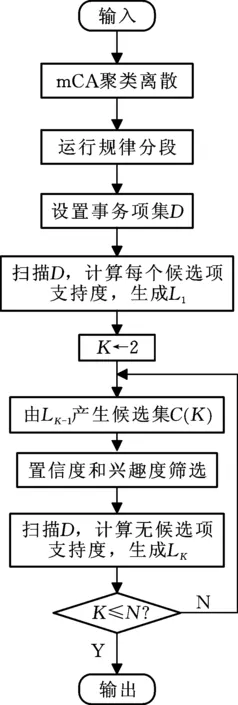
圖1 改進后的關聯規則算法流程圖Fig.1 Improved algorithm flow chart of association rules

2 故障預測模型

利用目標系統歷史測試數據、在線狀態監測和測試數據，提取橋式抓斗卸船機系統在運行過程中不同階段的狀態變量，分別建立故障類型與故障征兆的權重關系，故障征兆與反映卸船機狀態特征的關聯規則組之間的權重關系；將前述已監測的狀態參數數據作為建模數據，建立訓練數據驅動預測模型并對故障類型進行預測；最后進行故障預測結果判別。

2.1 故障類型與故障征兆權重關系

橋式抓斗卸船機實際運行過程中，當卸船機發生某一故障時，往往伴隨著多個故障征兆，同樣，一個故障征兆有可能對應多個故障類型[15]。因此，橋式抓斗卸船機故障預測的前提就是確定各種故障相對應的故障征兆。首先，確定橋式抓斗卸船機的故障類型及故障征兆，見表1。

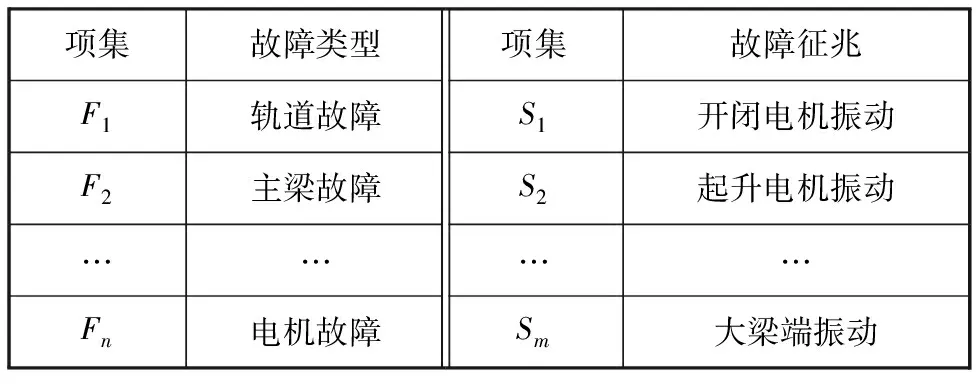
表1 卸船機故障類型及故障征兆

然后，采集相同工況下足夠多的歷史實驗數據作為樣本，分析故障類型與故障征兆之間的關聯性，在卸船機故障類型與故障征兆關聯分析中可以記：①事務數據庫Di={第i個故障類型Fi發生}；②項集Si={第i個故障征兆狀態超標}；③總樣本中，各故障征兆Sn發生的狀態量超標次數為f(Sn)；④故障例總數|Dm|中，各故障征兆Sn發生的狀態量超標次數為f(Sn∪Fm)；⑤關聯規則為Sn?Fm；⑥第m個故障類型Fm對應的約簡后故障征兆為Sm,n，Fm={Sm,1,Sm,2, …,Sm,Nm}，其中Nm為約簡后Fm中故障征兆個數。

由式(1)和式(2)分別求得關聯規則Sn?Fm的支持度S(Sn?Fm)和置信度C(Sn?Fm)。當支持度大于設定值時，認為此關聯規則有效，即Sn與Fm之間存在緊密的相互關聯關系。由置信度可得權重系數表達式：

(4)

式中，w′m,n為故障類型Fm中故障征兆為Sm,n的權重系數；Cm,n為相應的置信度。

2.2 故障征兆與關聯規則組權重關系

故障征兆與關聯規則組的權重關系實際上就是通過挖掘出的能表征卸船機狀態的關聯規則來反映與之相關的故障征兆。對每個關聯規則賦予權重時，應使故障征兆狀態特征中越重要的規則權重越大，并隨著數據信息的不斷更新對權值會有不同方位的收斂。根據各規則的屬性權重比wi/wj(i,j=1, 2, …,n)，構造權重比矩陣M：

其中，n是M的唯一非零特征根，記為λmax，而w是n所對應的特征矢量，并采用歸一化的特征作為權重矢量：

構建基于關聯規則支持度S、置信度C和興趣度I的權重計算公式：

(5)

其中，wi(Si,Ci,Ii)表示規則RAi在故障征兆狀態特征中的權重；Si、Ci、Ii分別表示該規則的支持度、置信度和興趣度。

2.3 構建預測模型

通過改進的興趣度量化關聯規則挖掘狀態參數數據中反映橋式抓斗卸船機狀態的關聯規則，在同一子系統和工況下，篩選可以反映故障征兆Sj參量的所有關聯規則RAj,k以及表征故障類型Fi的所以故障征兆Si,j，并分別計算故障征兆與關聯規則組權重關系以及故障類型與故障征兆權重關系相對應的權重系數，構造故障類型與關聯規則組的關聯規則指向性特征約束函數：

(6)

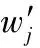
橋式抓斗卸船機故障預測步驟如下。

(1)利用改進的興趣度關聯規則算法挖掘能表征卸船機狀態的關聯規則RAj,k。

(2)建立橋式抓斗卸船機故障預測模型(圖2)，并計算相應的權重系數。

圖2 故障預測模型Fig.2 Fault prediction model

(3)計算關聯規則RAj,k的置信度變化率Δ，并代入故障預測函數式(6)。

(4)預測評估故障發生類型。其中，Fi為第i個故障類型，Si,j為對應第i個故障類型的第j個故障征兆，RA1,e、RAi,j、RAn,g分別為對應故障征兆的關聯規則。

通過橋式抓斗卸船機監測系統，獲取原始監測數據源，利用時域分析方法獲得以振動強度和應力值為特征的數據類型為數值型的數據庫。振動強度是指振動速度的有效值(均方根值)，能夠反映機械振動狀態簡明綜合、實用有效的特征量，其計算公式為

其中，v(n)為振動速度，N為所測信號長度，VRMS為振動強度能量值。以此數據庫為挖掘點，經上述預測模型流程進行故障預測。橋式抓斗卸船機故障預測流程如圖3所示。

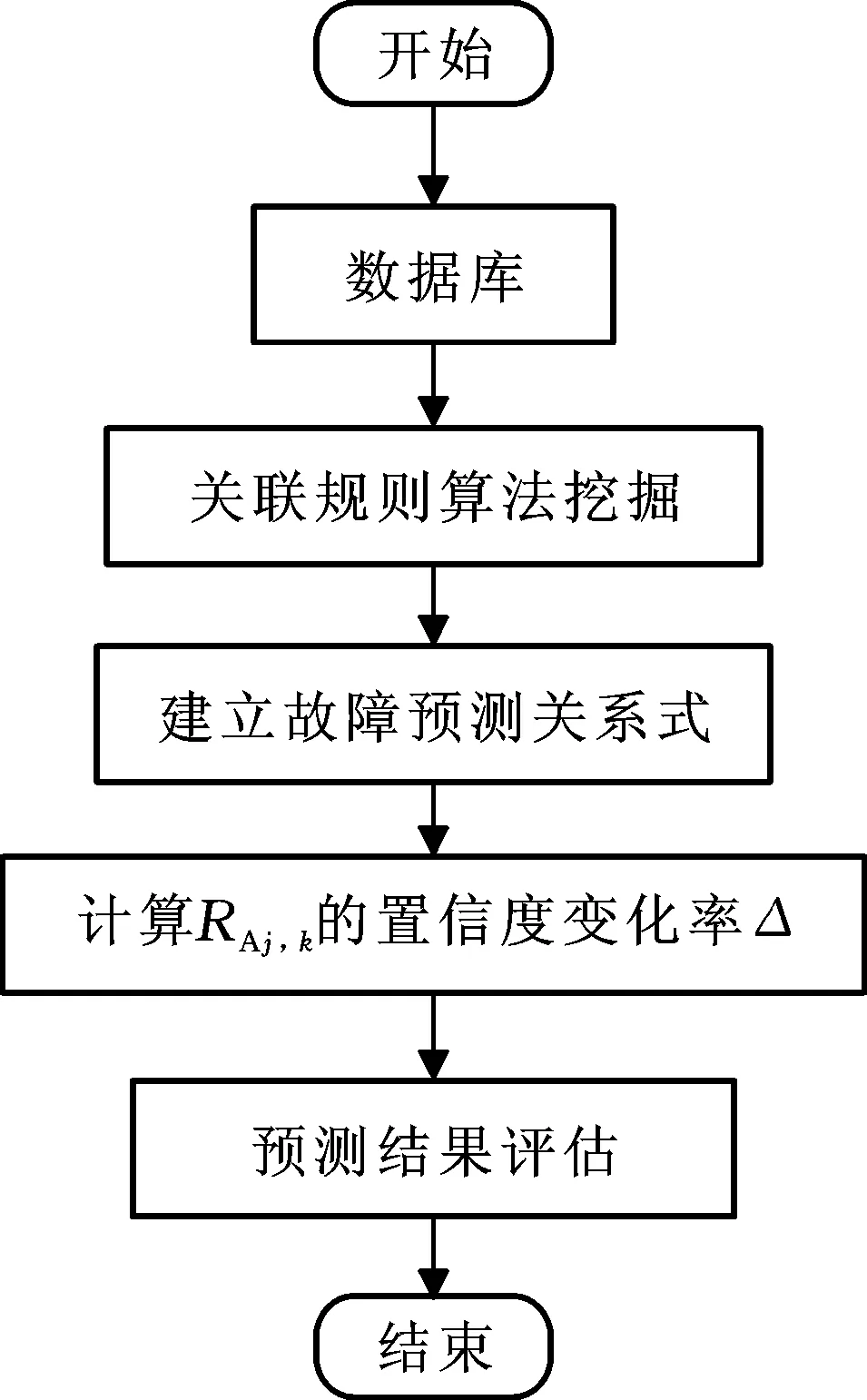
圖3 故障預測流程圖Fig.3 Flow chart of fault prediction

3 實例分析

3.1 監測數據源

針對某港口1號橋式抓斗卸船系統布置狀態監測傳感器，監測布置點見表2。采用該監測系統中2017年2～12月份的部分監測數據，每月選取500行數據，共5 000行，作為數據挖掘的數據源。橋式抓斗卸船機機械狀態在線監測的主要內容是四卷筒系統、變幅系統及大車運行系統中驅動電機和減速器的振動，金屬結構系統中大梁、小門架等金屬結構受力和軌道、大梁及小門架振動。為全面監測卸船機的機械狀態，在卸船機主要位置布置了37個傳感測點，這些測點按監測點位置分成5組：第Ⅰ組監測四卷筒系統驅動電機、減速器的振動；第Ⅱ組監測變幅系統驅動電機和減速箱的振動；第Ⅲ組監測大車運行系統驅動電機和減速器的振動；第Ⅳ組監測金屬結構系統中大梁、小門架及軌道上的振動與沖擊；第Ⅴ組監測大梁、小門架等金屬結構的受力情況。(X向：小車運行方向；Y向：垂直方向；Z向：大車運行方向)橋式抓斗卸船機機械狀態用各監測點測量的特征值表示。通過時域分析方法處理振動信號的原始數據，獲得各驅動電機、減速箱及金屬結構振動的振動強度特征值，大梁及拉桿等金屬結構的受力狀態用應力值表示。卸船機機械狀態在線監測過程中會產生海量的卸船機動態數據，這些數據將作為卸船機故障預測研究的數據源。

表2 卸船機監測點布置說明

3.2 關聯規則挖掘

為使對橋式抓斗卸船機狀態監測數據的關聯規則挖掘更有針對性，選擇狀態監測中組Ⅰ、組Ⅱ、組Ⅲ和組Ⅴ的監測點數據作為關聯規則的左側，組Ⅳ中的數據作為關聯規則的右側。首先，將采用的數據進行預處理，排除卸船機停機時和異常狀況下(包括惡劣天氣、設備故障)的異常數據，通過改進的Apriori算法挖掘，獲得表3所示的A9監測點振動烈度的部分數據聚類結果，振動強度數值將分為4類離散數據，從而將數值型數據轉化為布爾型關聯規則挖掘；然后，利用其算法通過支持度和置信度閾值采掘以及興趣度閾值過濾輸出關聯規則，考慮到實時采集數據和卸船機工作的特點，設定最小支持度為10.0%，最小置信度為50.0%，最小興趣度為1.5；最后，分別篩選獲取能表征四卷筒系統、變幅系統及大車運行系統機械狀態的關聯規則，部分關聯規則見表4～表6。

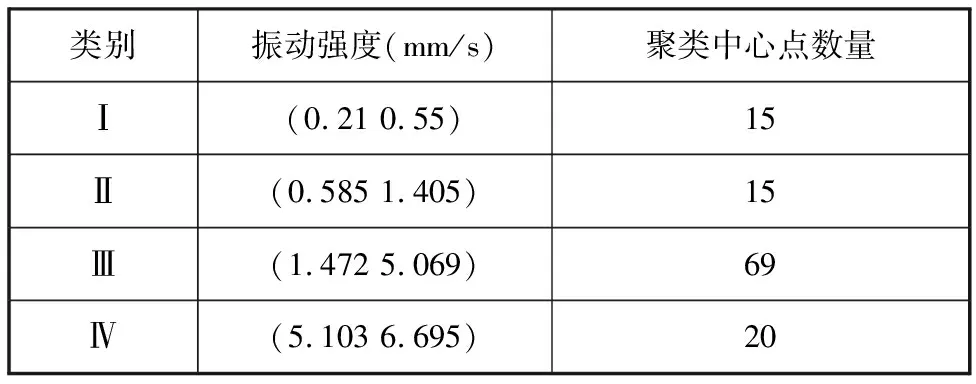
表3 A9監測點數據聚類結果

表4部分關聯規則是采用組Ⅰ和組Ⅴ獲取的監測數據對四卷筒中小車運行狀態的規則挖掘，由表4分析，規則1和8分別代表開閉和小車電機同時運作時的模式。規則2和7代表起升和小車電機共同運行時的模式。規則4為三者電機同時運作時的模式。規則3、5和6分別代表小車、起升和開閉電機單獨運行時的模式。

表5部分關聯規則是采用組Ⅱ和組Ⅴ獲取的監測數據對變幅系統運行狀態的規則挖掘，由表5分析，規則1代表變幅電機單獨運作時的模式。規則2代表整個變幅系統共同運作時的模式。規則3代表大梁變幅升降減速時的模式。

表4 四卷筒系統部分關聯規則

注：表中S、C、I變量分別表示支持度、置信度和興趣度的數值。括號內數據區間單位為mm/s。不再贅述。

表6部分關聯規則是采用組Ⅲ和組Ⅴ獲取的監測數據對大車運行系統運行狀態的規則挖掘，由表6分析，規則1和2分別代表大車1號和2號電機單獨運作時的模式。規則3表示大車減速運行過程中的模式。規則4代表大車運行系統整機共同運作時的模式。

表5 變幅系統部分關聯規則

表6 大車運行系統部分關聯規則

3.3 故障預測

橋式抓斗卸船機的故障種類很多，本文依據現有研究成果及現場的故障信息反饋，將卸船機系統常見故障類型分為6種，見表7。

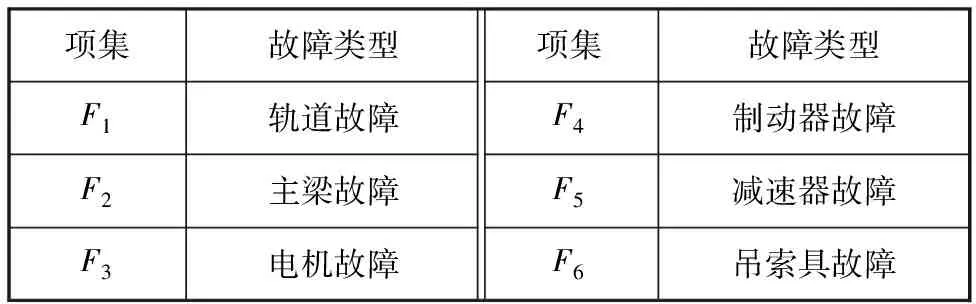
表7 卸船機的故障類型

橋式抓斗卸船機的狀態信息繁多，如果考慮所有狀態信息，故障預測體系將極為復雜，而且有些狀態信息模糊，不利于對卸船機進行預測評估。本文選取具有代表性且能準確有效反映卸船機運行狀態的狀態參量作為表征卸船機各類故障類型的故障征兆。最終選取表8中的24個狀態參量作為故障征兆進行狀態評估。

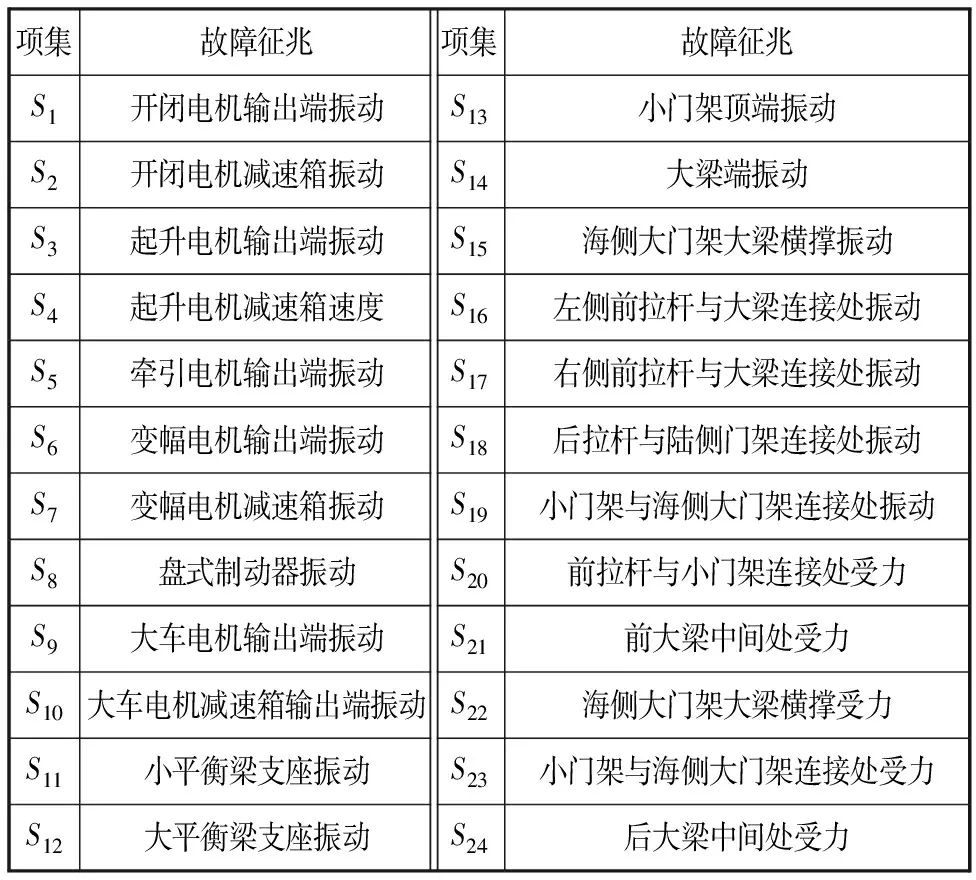
表8 卸船機的故障征兆

為了更明確地描述設備故障預測模型的實現過程，不失一般性，只給出小車運行狀態故障預測分析，整理分析由某港口起重機械有限公司提供的關于小車運行系統的部分歷史試驗數據(表9)。

表9 小車系統歷史測試樣本數據

根據表9中故障類型所對應的故障征兆的支持度，利用最小支持度閾值對其進行簡化，建立卸船機小車運行系統故障類型與故障征兆的關聯關系，見表10。

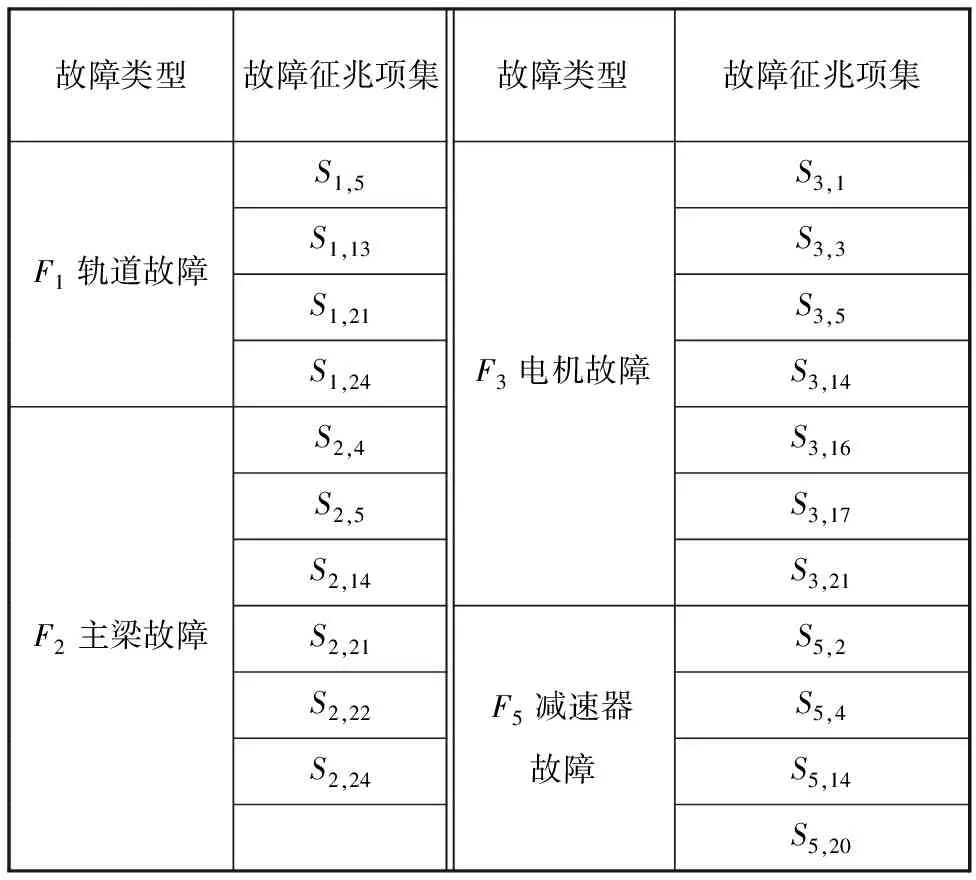
表10 故障類型與故障征兆的關聯關系

以下故障預測以小車運行系統中“軌道故障”F1為故障預測實例，計算其對應故障征兆的權重系數。記事務數據庫D1={軌道故障}，且|D1|=|F1|=135，N1=4。故障征兆S1,5、S1,13、S1,21、S1,24在F1中的超標次數分別為110, 120, 130, 103；在總樣本中的超標次數分別為330, 126, 365, 190。由式(2)可得這4個故障征兆在軌道故障中的置信度：C1,5=33.3%,C1,13=95.2%,C1,21=35.6%,C1,24=54.2%。將計算得到的置信度代入式(4)可得相應的權重系數：w′1,5=0.153,w′1,13=0.436,w′1,21=0.163,w′1,24=0.248。

以上述F1為例，通過小車運行系統關聯規則輸出表中關聯規則與故障征兆狀態參量之間的關系，建立故障征兆S1,1、S1,2、S1,3、S1,4(即S1,5、S1,13、S1,21、S1,24)與卸船機狀態關聯規則組之間的關系，并利用權重計算式(5)計算其權重系數，見表11。

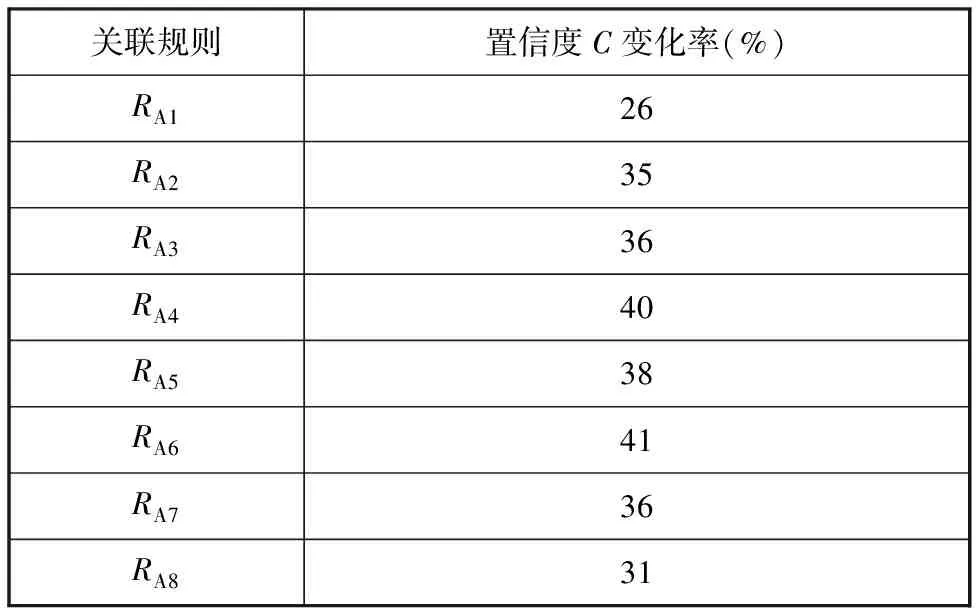
選取“軌道故障”F1發生前一個月的歷史數據作為實驗驗證數據，通過RA數值波動圖，其中RA3((A9,A10,S2,S3)?D4)關聯規則部分數據波動如圖4所示，分別計算表11對應的標準關聯規則的置信度變化率，見表12，通過判斷標準關聯規則的穩定性，獲得反映卸船機狀態的改變程度，根據現場故障信息反饋以及經驗知識，設定故障預測函數閾值為30%。將表12中置信度變化率代入故障預測函數式(6)，求得F1的故障預測

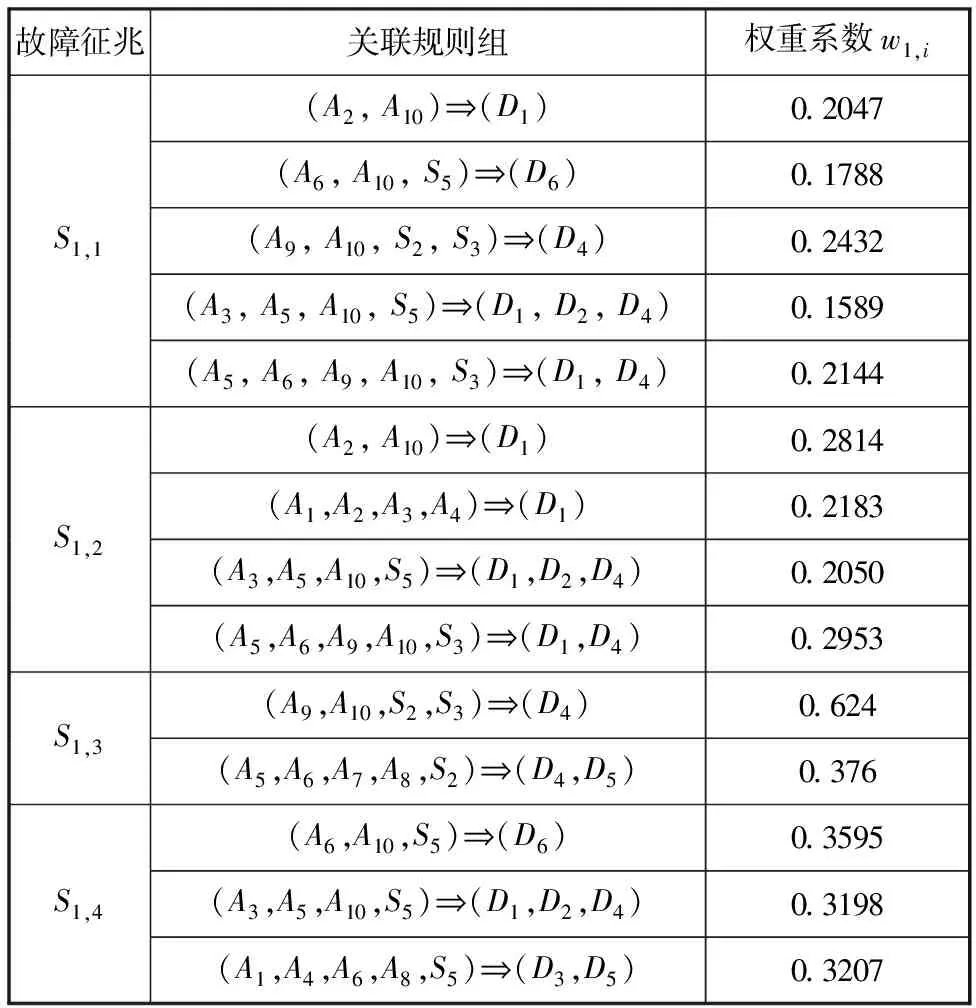
表11 故障征兆與關聯規則組權重系數表

函數值為36.865%，其函數值大于設定故障預測閾值，可實現故障預測。

圖4 RA3數值波動圖Fig.4 RA3 numerical wave diagram

關聯規則置信度C變化率(%)RA126RA235RA336RA440RA538RA641RA736RA831

“軌道故障”F1故障預測只是其中一個故障案例，不失一般性，其他故障類型同樣可以用相同的權重興趣度關聯規則預測方法對橋式抓斗卸船機故障類型進行預測，實驗結果表明，該方法可有效地預測故障發生前的故障信息變化狀態，以便提前做出技術處理，避免故障發生，對提高企業的經濟效益具有現實意義。

4 結論

(1)采用興趣度關聯規則算法獲取能夠表征卸船機狀態特征的關聯規則，通過計算支持度、置信度和興趣度，分別得到卸船機故障類型和故障征兆狀態量的權重系數、故障征兆和規則組的關聯耦合關系以及權重系數，一定程度上避免了專家意見或經驗的主觀性的問題；利用上述兩兩參數間的權重系數構建卸船機故障預測函數模型，通過實際關聯規則狀態變化的對比捕捉早期微弱的機械故障狀態變化信息。

(2)實例分析結果表明，多種數據分析方法的融合運用能夠獲取較好的狀態評估和故障預測效果，并且在多故障問題的處理中也表現良好，具有較好的可預測性和準確性。