自然循環工況下離心泵阻力特性的實驗研究與數值模擬

李偉通，于 雷,*，郝建立，李明芮，胡高杰,2

(1.海軍工程大學 核科學技術學院，湖北 武漢 430033；2.92609部隊，北京 100077)

非能動安全系統是新一代先進反應堆的核心標志。通過提高核動力裝置自然循環能力，實現非能動安全系統功能是研究的熱點問題。研究表明，熱源熱功率、冷熱源相對位差、流體流動的阻力等關鍵因素制約了自然循環能力的提高[1]。對于某型壓水堆核動力裝置，一回路由強迫循環過渡至自然循環時主泵停轉，自然循環下系統的阻力特性與強迫循環相比有較大區別，尤其是主泵的流動阻力占一回路總阻力的比例可達60%，嚴重影響自然循環流量的提升。此外，當非能動余熱排出系統運行時，蒸汽發生器倒流量可能會大于正流量，反應堆出現局部反向流動現象[2]，即冷卻劑從反應堆進口處經主泵、蒸汽發生器等反向流入到反應堆出口處，導致衰變熱排出途徑不暢，但關于泵反向阻力特性的研究較少。由于離心泵的幾何流道的變化和復雜性，很難從理論上獲得通用的阻力公式，給阻力計算帶來了很大的不確定性。因此，采用適當方法對離心泵的阻力特性進行研究，對泵的設計和優化尤為重要，也可為安全分析提供理論依據。

公開文獻中，一些學者針對特定結構的阻力特性取得了較多成果，具有重要借鑒意義。基于實驗，Stevens[3]提出了適用于非能動換熱器管束阻力特性的經驗公式；Rehme[4]針對定位格架提出了經典的阻力模型；Cigarini等[5]、Schikorr等[6]在Rehme模型基礎上進行了適用性分析；Chenu等[7]比較了多種定位格架阻力公式并應用于TRACE程序。此外，CFD方法也用于阻力特性的研究。Abbasian等[8]、Jin等[9]比較了CFD湍流模型對模擬結果的影響；Batta等[10]分析了粗糙度、邊緣特征對定位格架阻力特性的影響。然而，關于離心泵阻力特性的研究較少。本文基于離心泵的阻力模型，通過實驗與數值模擬相結合的方法，對低流量自然循環工況條件下的離心泵阻力特性進行研究。其中，利用實驗方法獲得泵正向、反向損失系數的經驗關系式；利用CFD方法模擬離心泵內部流動狀態，探索流體能量損失的主要區域。

1 阻力模型

管內流動的能量損失可分為兩類，即沿程損失和局部損失。與充分發展流體中的沿程損失不同，局部損失的形成主要是流體相互碰撞并形成漩渦造成的。當流體通過停轉的離心泵時，流經葉輪、導葉等多個較為復雜的流域，此時流體流場分布極不均勻，一般將全部損失Δp表示為：

(1)

以揚程損失的形式對式(1)進行改寫，則損失系數可表示為：

(2)

式中：K為損失系數；ρ為密度；v為流速；Q為體積流量；A為泵出口流道流通面積；ΔH為揚程損失。

損失系數的準確性對于分析整個反應堆系統的流動特性具有重要意義。在利用RELAP5等大型系統分析程序進行建模時，與管道等部件損失系數的輸入不同，通常通過構建泵的特性曲線模型來模擬泵的流動阻力。由泵的主要參數及其額定值進行無量綱化，得到揚程比h、轉速比α和流量比q，再轉化為泵全特性曲線來表征泵的運行狀態，如圖1所示。其中，HVN等無量綱曲線的分類列于表1。

圖1 典型離心泵的無量綱揚程曲線[11]Fig.1 Homologous head curve of typical centrifugal pump[11]

泵特征揚程分曲線橫坐標縱坐標正向流動,正向轉速HANq/αh/α2HVNα/qh/q2反向流動,正向轉速HADq/αh/α2HVDα/qh/q2反向流動,反向轉速HATq/αh/α2HVTα/qh/q2正向流動,反向轉速HARq/αh/α2HVRα/qh/q2

自然循環工況下泵停轉(α/q=0)，對應HVN和HVR(或HVD和HVT)曲線的交點，2個點分別代表正向流動和反向流動。將對應點的無量綱揚程坐標(h/q2)用C表示，則可得到無量綱參數與損失系數的關系式：

(3)

式中：H為揚程；下標R代表額定工況。

由式(3)可見，RELAP5程序中離心泵的損失系數為固定值。對于形狀相對簡單的管段，如突擴突縮截面，損失系數可由理論分析的方法進行推算，如采用面積突變模型等。對于離心泵等內部流道復雜的結構，較難從理論上進行推導，通過實驗方法進行損失系數的測量則較為準確。然而在實際應用中，反應堆主泵通常只完成第一象限曲線(泵正常運行)的實驗，僅有少量泵進行了正向、反向流動阻力的實驗，如SEMISCALE泵、BETHSY泵、ATLAS泵[12]，有時甚至只有泵的額定值數據可用，計算時只能借助其他泵數據。對于不同的離心泵，C的差別較大，不利于自然循環等特殊工況的準確模擬。

2 實驗研究

2.1 實驗系統及流程

實驗系統(圖2)主要包括實驗主回路、測量儀表、補水排水裝置和數據采集裝置。其中，實驗主回路為開式循環回路，主要由輔助驅動泵、被測試離心泵、水箱、調節閥門及相應的管道組成。實驗中采用輔助泵提供低驅動壓頭，模擬自然循環低流量條件[13]，參數如下：QR=20.0 m3/h，NR=2 900 r/min，HR=50 m。

圖2 實驗系統示意圖Fig.2 Schematic of experimental facility

被測試泵軸采取固定措施。為分別實現對泵正向、反向阻力特性的測量，回路設計中利用可拆卸盲板等設備，可較為方便地改變流體流動方向，如圖3所示。此外，實驗段設計為多個支路，可實現多臺泵的獨立測量，也可拓展進行其他阻力部件的研究。

實驗段流量由電磁流量計測量，實驗段壓力損失由壓差變送器測量。由于流體在泵進出口處可能產生較大的碰撞和擾動，為減小測量誤差，壓差變送器的引壓管設置在泵進口前和出口后10D位置(D為管道直徑)。此外，雖然實驗用水為常溫水，但由于輔助泵長時間運行可能會產生較大熱量，采用K型熱電偶對實驗回路溫度進行測量，在輔助泵出口處安裝壓力變送器以監測泵的運行狀態。為方便對所測量的各類參數進行處理，基于Labview軟件和信號轉換裝置進行數據采集。

圖3 阻力特性測量流程圖Fig.3 Measurement schematic of flow characteristics

2.2 不確定度分析

由于不可能獲得實驗真實值，在實際情況下需分析實驗數據的準確性以及分散度，即數據的不確定度。實驗中的誤差主要來自測量裝置、信號轉換裝置和數據采集裝置，應用RSS方法對不確定度進行分析[14]。

流量測量的不確定度uF可表示為：

(4)

其中：uf為流量計的不確定度；uI/V為I/V轉換裝置的不確定度；ud為數據采集裝置的不確定度。

溫度測量的不確定度uT可表示為：

(5)

其中：uth為熱電偶的不確定度；utt為溫度變送器的不確定度。

壓降測量的不確定度uP可表示為：

(6)

其中，upt為壓差變送器的不確定度。

根據式(1)，由于流體密度的變化小于0.1%，其誤差可忽略，損失系數的不確定度uK應為壓降和流量的間接不確定度，表示為：

(7)

2.3 實驗結果

實驗過程中通過調節流量獲得離心泵的壓降特性。隨著流量的增加，壓降曲線呈拋物線式增長，且多次調節流量得到的壓降曲線基本一致，驗證了實驗的可重復性。

圖4為實驗得到的離心泵正向、反向損失系數。雷諾數采用泵出口參考點進行計算，即Re=ρvDh/μ[15]。可看出：在較高雷諾數下損失系數基本保持不變，這與文獻[12]的泵實驗結果一致；在相同的雷諾數下，反向壓降明顯高于正向壓降。此外，當雷諾數低于8×104時，損失系數隨雷諾數的降低有明顯增大的趨勢，最大可達20%，而文獻[12]對低雷諾數下損失系數的測量不準確，未得到明確關系。基于實驗數據，通過擬合方式得到了損失系數的經驗關系式。關系式采用a+b/Rec形式[16]表示：

(8)

其中：a為基準損失系數；b、c為經驗系數；Re=2.0×104～1.5×105。

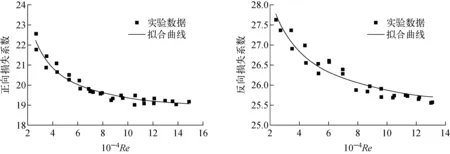
圖4 損失系數的變化Fig.4 Variation of loss coefficient

與定位格架局部損失系數相關的研究中有類似現象，Kim等[17]通過實驗得到了大量經驗關系式，但僅限于正向損失。其中，Mochizuki提出的經驗關系式[18]與本文形式雖不同，但流動工況與本文實驗范圍較接近，基準雷諾數為8×104。文獻[14]的研究也表明，損失系數在低雷諾數工況下迅速變化。進而推測復雜結構的阻力特性具有一定的相似性。

此外，研究表明，不同結構棒束的損失系數表達式具有較大區別[19]，而基于此實驗臺架對另一型號泵的研究結果與式(8)有所區別，但形式相似，進一步說明損失系數確實需要進行修正，式(8)具有普遍性。前文指出，RELAP5程序中離心泵的損失系數為固定值，并不適用于自然循環工況的分析。因此，可參考文中的修正公式對模型進行修改。

3 數值模擬

3.1 三維建模及網格劃分

利用Solidworks軟件對離心泵流體域進行建模，主要包括進口管段、進口腔室、葉輪區域、導葉區域、出口腔室和出口管段。為消除進出口效應對流態的影響，對進、出口管段進行了適當延長建模。針對研究對象的復雜程度，利用ICEM軟件進行混合網格劃分，以兼顧準確計算和快速劃分。其中，對于泵進、出口管段，采用結構化網格；對于泵內部復雜結構，采用非結構化網格。初步分析表明，葉輪、導葉區域對計算結果影響較大，對其網格進行局部加密。經網格質量檢查和無關性分析，最終確定總網格數約為2.2×106。

3.2 計算模型及條件

利用Fluent軟件進行模擬計算。文獻[14]的研究表明，不同湍流模型會對模擬結果產生影響，模型的適用性有待驗證。經初步計算篩選，本文計算時采用了SSTk-ω模型、RNGk-ε模型和標準k-ε模型。計算介質為常溫水，采用質量流量入口和壓力出口邊界，壁面處采用無滑移邊界條件，殘差收斂精度設置為10-4。

3.3 模擬結果

圖5為CFD計算與實驗的誤差對比。可看出，3種湍流模型的計算值整體偏高，正向計算較反向計算誤差大。相比之下，RNGk-ε模型與實驗值的相對誤差在10%以內，變化規律與實驗值更接近，在進一步分析中選用了此模型。由于CFD方法能重現實驗結果且便于反映泵的復雜結構特征，在對泵的結構進行優化和改進時，CFD方法特別適用于對阻力特性進行預測。

圖5 損失系數計算值與實驗值比較Fig.5 Comparison of calculated values with experimental data for loss coefficient

圖6為正向流動和反向流動的流線及流速分布(Re=1.2×105)。從圖6可看出，反向流動的速度分布更加不均勻，流體的撞擊和回流現象突出，葉片中心及末端均出現了與主流明顯分離的漩渦，且出現了較高的局部速度。而正向流動在葉輪處的分布流暢，僅在導葉流道內出現了較大速度變化。

圖7為正向流動和反向流動的壓力分布(Re=1.2×105)。從圖7可看出，流體在主要流道的交界區域出現了明顯的壓力損失，如出口腔室、導葉、葉輪等處，且正向、反向流動的壓力分布存在明顯區別。正向流動時壓力損失的方向與反向流動時基本相反，且正向損失突出集中在導葉流道內，而葉輪內損失占比在10%以下；反向損失時葉輪內則有20%以上的損失。

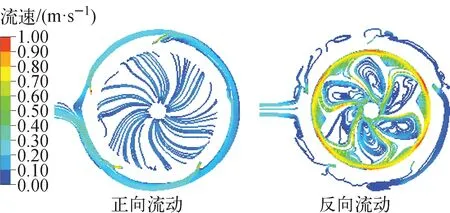
圖6 流線及流速分布對比Fig.6 Comparison of streamline and velocity distribution

實驗中出現了反向壓降高于正向壓降的現象，而CFD計算表明，泵內部流道多變是導致這一現象的根本原因。流體過流區域不對稱、導葉流道偏窄、葉輪變化復雜，導致漩渦、回流等現象的出現，而正、反向流道阻塞的情況有所不同，速度流場差異較大；改變了流體做功情況，進一步造成了壓力損失分布的區別。

圖7 壓力分布對比Fig.7 Comparison of pressure distribution

此外，實驗中出現了損失系數隨雷諾數的降低而明顯增大的趨勢，而CFD計算表明不同雷諾數下的局部流動存在區別。以反向流動工況為例，圖8為不同雷諾數下的湍動能分布。可看出，低雷諾數下，在出口腔室與出口管道交界區域、導葉與葉輪交界區域存在局部較高湍動能，表明流體流經此處時湍流強度有較大的提升，能量損失較大，而隨著雷諾數的增加，局部高湍動能的現象有所減弱。說明泵復雜的流道對低流量下流體的出流影響更大，流體的局部流動更不穩定，導致出現更大的損失系數。

圖8 湍動能分布對比Fig.8 Comparison of turbulent kinetic energy distribution

4 結論

針對自然循環時離心泵阻力特性帶來的不確定性問題，通過實驗與數值模擬方法，對低流量下離心泵阻力的變化規律進行了研究，得出以下結論。

1) 相同雷諾數下，反向壓降明顯高于正向壓降；雷諾數大于8×104時，損失系數基本保持不變，而低雷諾數下損失系數隨雷諾數的降低有增大的趨勢；基于實驗得到了離心泵損失系數的經驗關系式。

2) CFD方法能較好地預測損失系數，RNGk-ε模型與實驗值的相對誤差不超過10%。通過CFD模擬，解釋了實驗中的特殊現象。離心泵的壓力損失主要集中在葉輪、導葉等結構的交界區域；正向流動與反向流動的流場分布存在顯著區別；低雷諾數下局部流動更加不穩定。

研究結果可增強對自然循環中離心泵流動特性的認識，對離心泵的優化設計和計算模型的改進具有借鑒意義。后續可結合該泵的結構特點，對幾何特征的影響因素進行更詳細的分析研究。