Time evolution of angular momentum coherent state derived by virtue of entangled state representation and a new binomial theorem?
Ji-Suo Wang(王繼鎖), Xiang-Guo Meng(孟祥國), and Hong-Yi Fan(范洪義)
1Shandong Provincial Key Laboratory of Laser Polarization and Information Technology,College of Physics and Engineering,Qufu Normal University,Qufu 273165,China
2Shandong Provincial Key Laboratory of Optical Communication Science and Technology,School of Physical Science and Information Engineering,Liaocheng University,Liaocheng 252059,China
3Department of Material Science and Engineering,University of Science and Technology of China,Hefei 230026,China
Keywords:invariance of angular momentum coherent state,entangled state representation,new binomial theorem,time evolution
1.Introduction
Coherent state theory has been widely used in quantum optics and laser physics.The optical coherent state with the amplitude α is defined as[1–4]
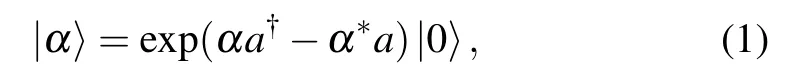
where a and a?are respectively boson annihilation and creation operators,It has been common knowledge that the Hamiltonian

can keep form-invariant for coherent state,i.e.,if the initial state is a coherent state,it will evolve into still a coherent state.In this work we search for which kind of Hamiltonian can maintain the form of angular momentum coherent state(AMCS),the AMCS is defined as[5–9]
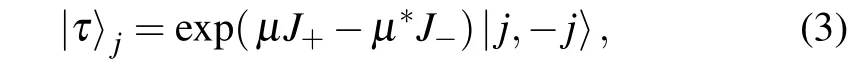
where J+and J?are raising and lowering operators of angular momentum,respectively,obeying the following commutative relations andis the lowest weight state annihilated by J?,i.e.,Using the disentangling formula

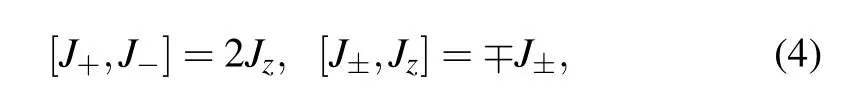
whereμ=(θ/2)e?i?and τ=e?i?tan(θ/2).Equation(3)becomes

Jzhas its eigenstate
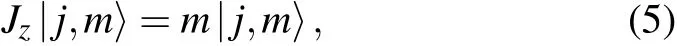
We shall begin with the boson realization of AMCS to proceed our discussion. We then introduce the entangled state representation and derive a new binomial theorem involving two-subscript Hermite polynomials to go on.It turns out that the wave function of AMCS in the entangled state representation is classified as single-subscript Hermite polynomials H2j. Based on this result and the recursive property of H2jwe find that the Hamiltonian H=f(t)J++f?(t)J?+g(t)Jzcan maintain the form-invariance of AMCSand the value of τ(t)is totally determined by f(t),f?(t),and g(t).
The rest of this paper is arranged as follows. In Section 2 we reform the angular momentum coherent statein boson realization and show that it is an entangled state.In Section 3 we set up the entangled state representation and introduce the two-subscript Hermite polynomials.In Section 4 we deduce the generalized binomial formula which involves two-subscript Hermite polynomials. In Section 5 we obtain the wave function ofin the entangled state representation.
In Section 6 we examine the form-invariance of AMCS during time evolution and determine the value of τ(t).
2.Angular momentum coherent state in boson realization
Using Schwinger boson realization of angular momentum operators
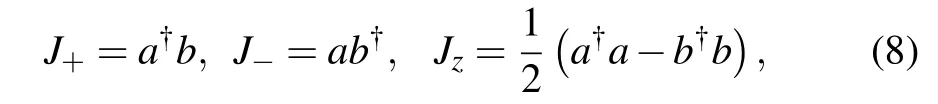
the eigenstate of Jzis
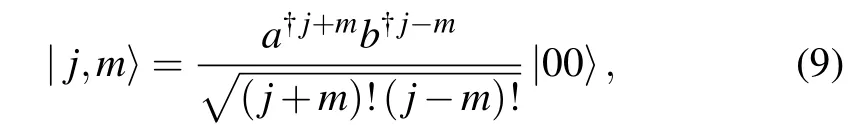
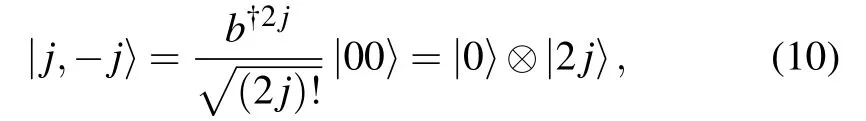
and we can reform the AMCS in Eq.(7)as
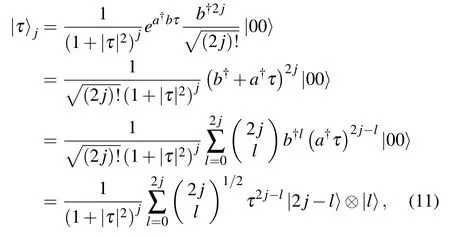
which exhibits quantum entanglement between the two modes,this enlighten us to introduce the entangled state representation to study
3.The entangled state representation and the two-subscript Hermite polynomials
In Refs.[10]and[11],the unnormalized continuousvariable entangled statewhich is the common eigenvector ofand,noting,has been constructed as follows:

which takes the two-subscript Hermite polynomials Hm,n(ζ,ζ?)as its expansion function in the two-mode Fock space
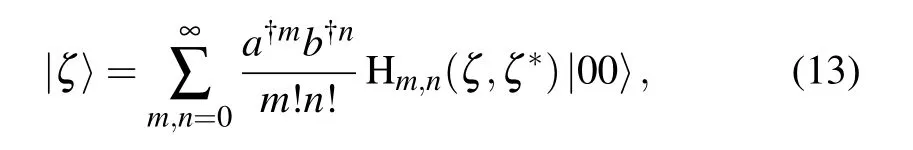
here Hm,n(ξ,ξ?)can be either defined through its generating function[12,13]
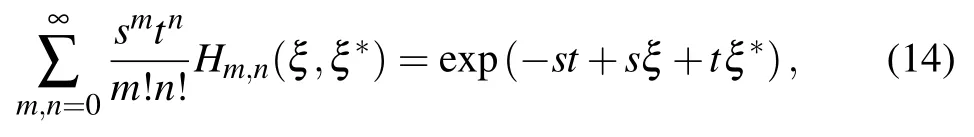
or by its power-series expansion
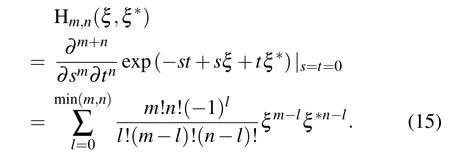
Note that Hm,nis not a direct product of two independent single-subscript Hermite polynomials. Hm,nhave their own uses in studying quantum optics and light propagation modes in quadratic graded-index media.From Eq.(13)we see
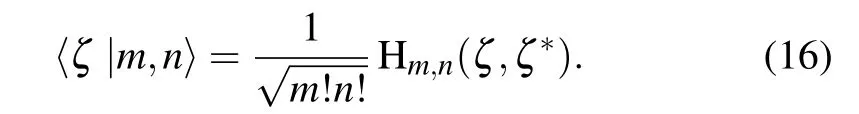
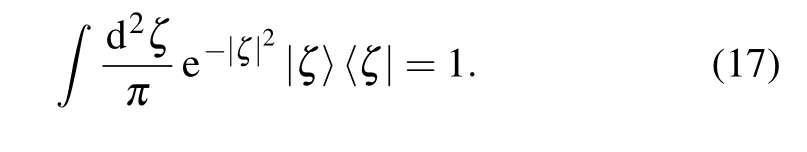
4.A generalized binomial formula involved twosubscript Hermite polynomials
From Eqs.(11)and(16)we see the wave function
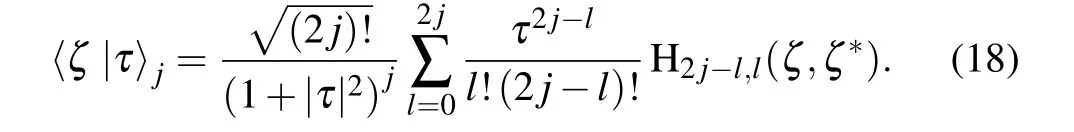
We are challenged to make the summation in Eq.(18),which involves H2j?l,l.Instead of directly doing this,we try to prove a generalized binomial formula by considering
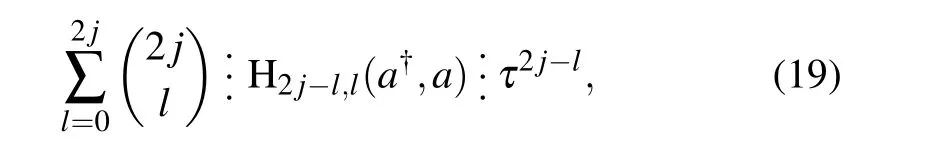
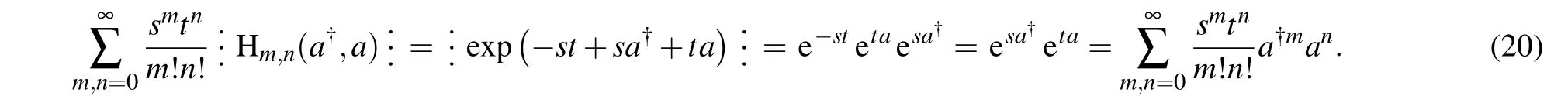
Comparing smtnon both sides of Eq.(20)we have the operator identity
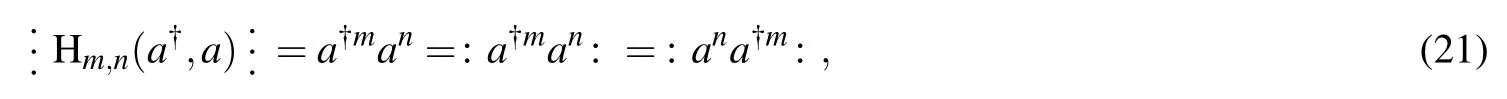
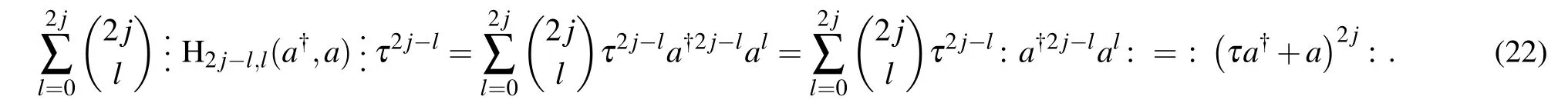
By making up
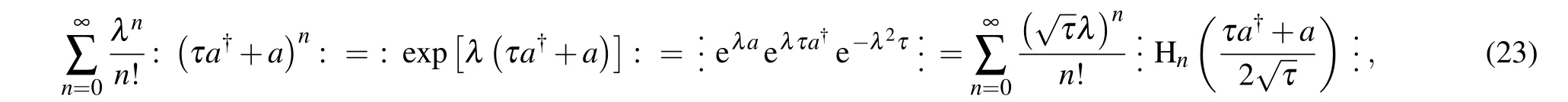
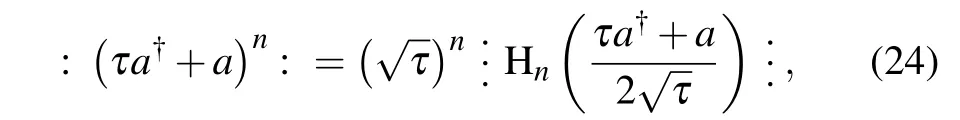
therefore equation(22)becomes
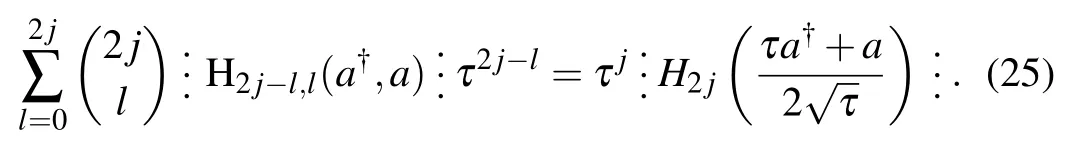
Since the two sides of Eq.(25)are both in antinormal ordering,so we obtain a new generalized binomial formula
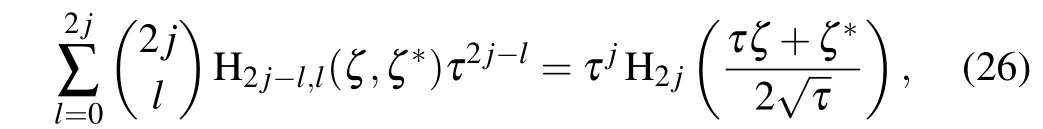
its right-hand side appears as a single-subscript Hermite polynomial.Further,let

Equation(18)becomes
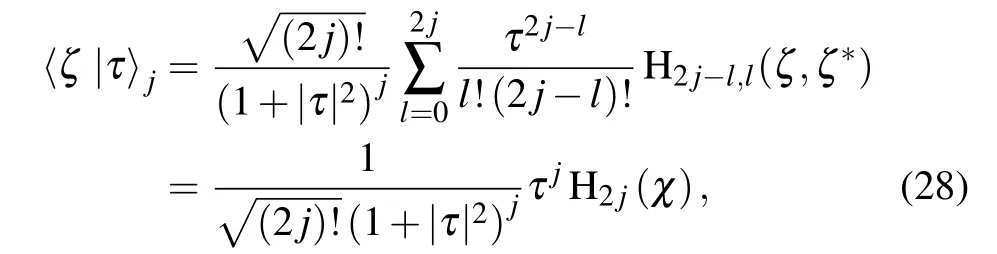
here H2jdenotes the single-subscript Hermite polynomial of order 2j.Hence the wave function of angular momentum coherent state in the entangled state representation is classifies as H2j(χ).This brings convenience for further studying
5.Time evolution of AMCS
As an application of the above theory,we consider the system described by the Hamiltonian
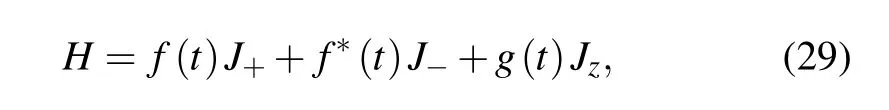
and supposing it initially is in angular momentum coherent statewe wish that it still evolves into an angular momentum coherent state,which meansthen the Schr?dinger equation is
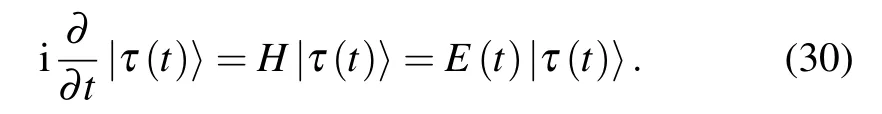
Inserting the completeness relation of entangled states in Eq.(17)

and using the following relations
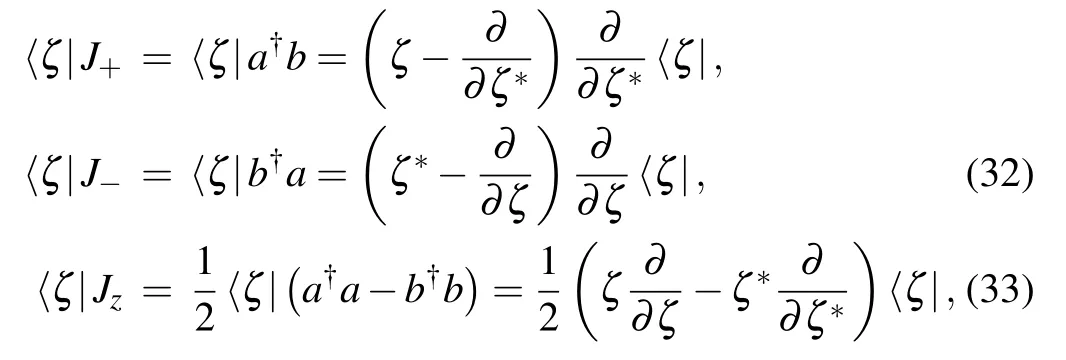
we have
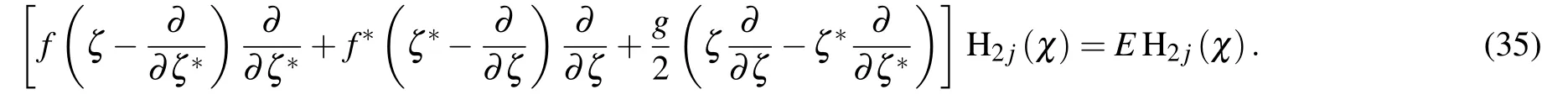
Noting χ in Eq.(27),so
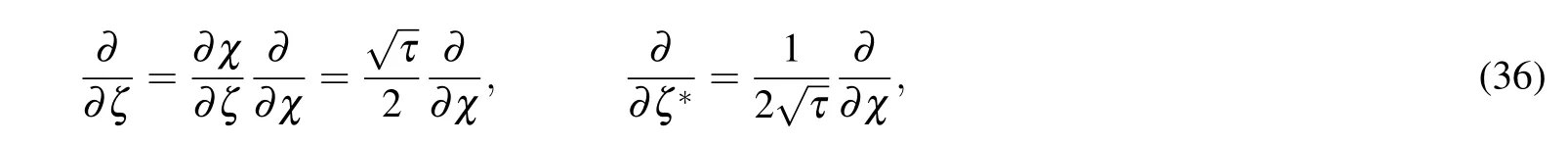
and using the property of Hn(χ)(Refs.[6]and[20])
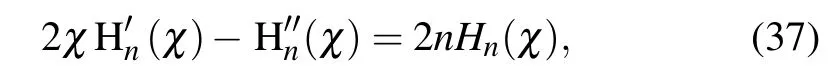
we can respectively express the terms in Eq.(35)as
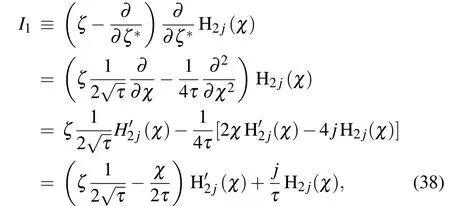
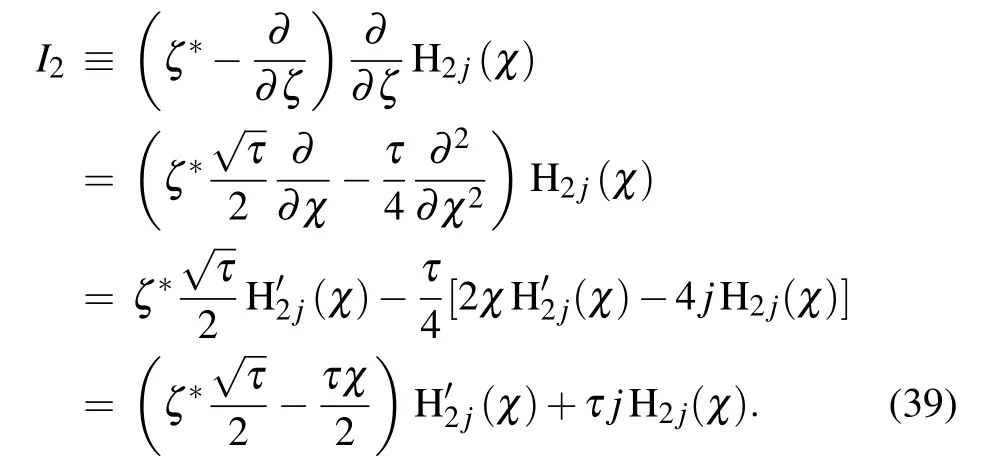
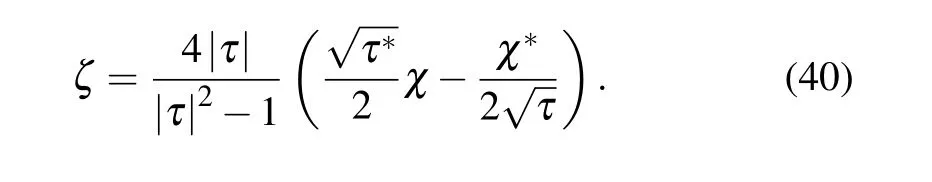
Thus equation(38)becomes
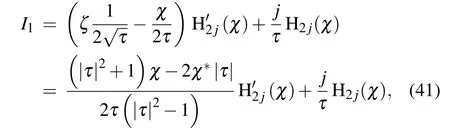
while equation(39)takes the form
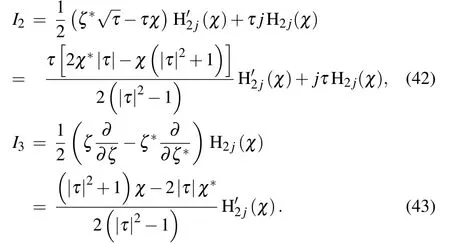
Then the eigenfunction equation is

Since

and the Hermite polynomials of different orders are mutual orthogonal,comparing the two sides of Eq.(44)we finally obtain

and

Because the eigenvalue equation cannot depend on the entangled state parameter ζ,then cannot depend on χ either,we have the value of τ,that is

which is totally determined by the parameters in the Hamiltonian(29).Moreover,we know the eigenvalues are
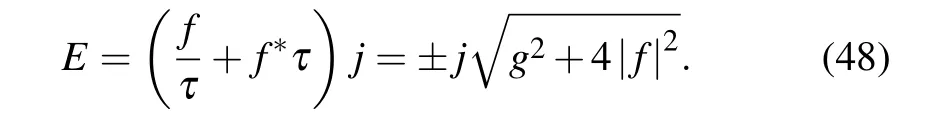
In summary,we have studied how an angular momentum coherent statekeeps its form-invariant during time evolution governed by the Hamiltoniang(t)Jz.By employing the entangled state representationand deriving a new binomial theorem involving two-subscript Hermite polynomials we have derived the wave functionwhich is a single-subscript Hermite polynomial.Based on this result the time evolution of angular momentum coherent state is examined,and the value of τ(t)is determined.It should be noted that our idea can be generalized to many other quantum entangled systems:using recursion relations of new binomial theorem involving special functions to convert differential operation to algebraic operation.
- Chinese Physics B的其它文章
- Theoretical analyses of stock correlations affected by subprime crisis and total assets:Network properties and corresponding physical mechanisms?
- Influence of matrigel on the shape and dynamics of cancer cells
- Benefit community promotes evolution of cooperation in prisoners’dilemma game?
- Theory and method of dual-energy x-ray grating phase-contrast imaging?
- Quantitative heterogeneity and subgroup classification based on motility of breast cancer cells?
- Designing of spin filter devices based on zigzag zinc oxide nanoribbon modified by edge defect?

